刷题之最长公共/上升子序列问题

目录

一、最长公共子序列问题（LCS）

1、题目

 2、题目解读

​编辑

 3、代码

四、多写一题

五、应用

二、最长上升子序列问题（LIS）

1、题目

 2、题目解读

 3、代码

四、多写一道

 Ⅰ、题目解读

 Ⅱ、代码

一、最长公共子序列问题（LCS）

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。一个数列 ，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。

1、题目

最长公共子序列

我们有两个字符串m和n，如果它们的子串a和b内容相同，则称a和b是m和n的公共子序列。子串中的字符不一定在原字符串中连续。
例如字符串“abcfbc”和“abfcab”，其中“abc”同时出现在两个字符串中，因此“abc”是它们的公共子序列。此外，“ab”、“af”等都是它们的字串。
现在给你两个任意字符串（不包含空格），请帮忙计算它们的最长公共子序列的长度。

 

输入描述:

输入包含多组数据。
每组数据包含两个字符串m和n，它们仅包含字母，并且长度不超过1024。

 

输出描述:

对应每组输入，输出最长公共子序列的长度。

示例1

输入

abcfbc abfcab
programming contest
abcd mnp

输出

4
2
0

 2、题目解读

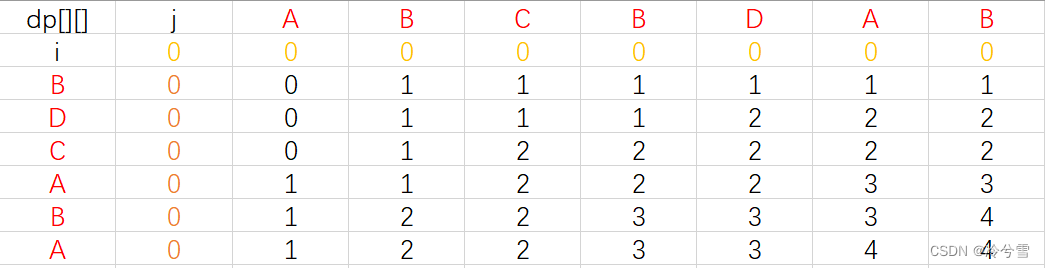
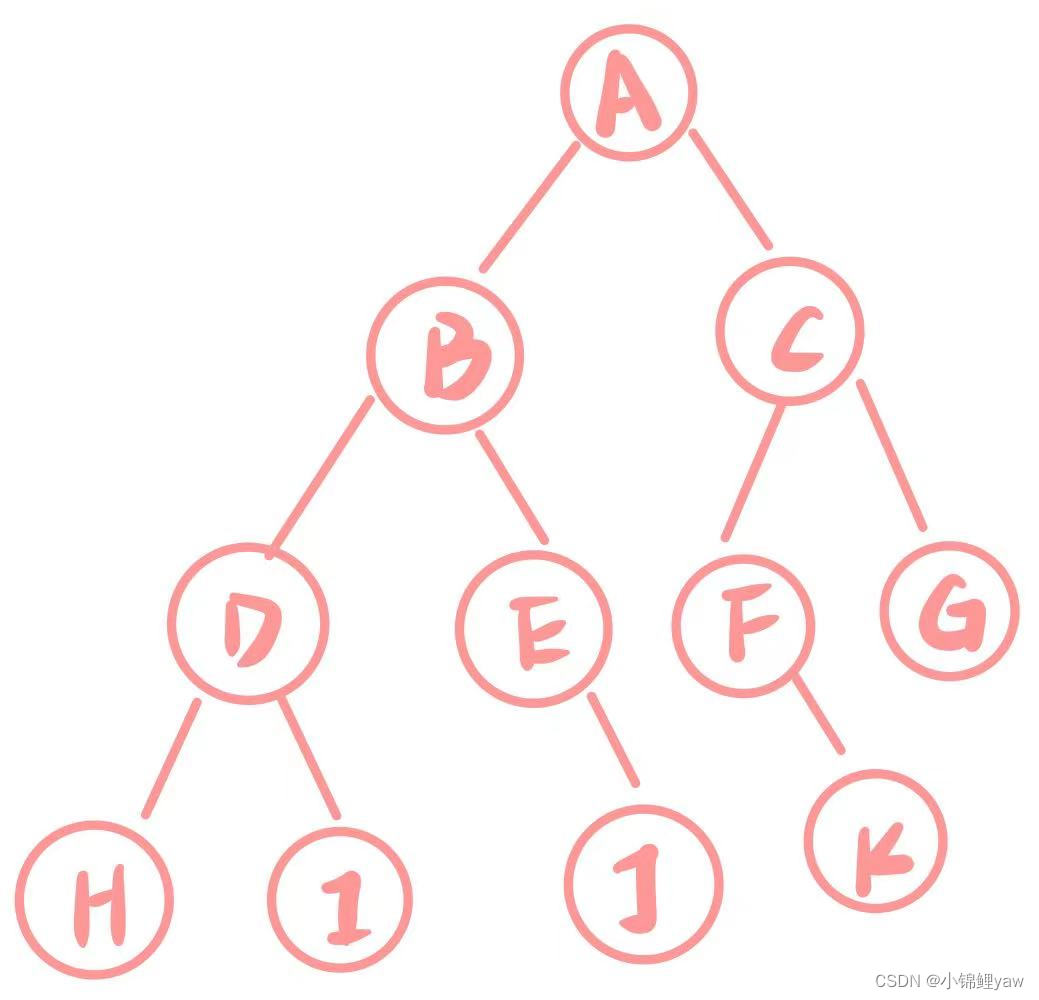
如题所示，题目会给我们两个字符串，要求我们去寻找最长的公共子序列。下面我举ABCBDAB和BDCABA这个例子，我们先用肉眼发现一下有三个长度都是四的子序列。

这是一个非常经典的动态规划题，我也废话不多说，接下来直接说解决这个问题最常见的方法：创建一个二维数组dp[][],用dp[i][j]来存储s1前i个字符和s2前j个字符的LCS数，我们想一下dp[i][j]和dp[i+1][j+1]有什么关系，发现 假如s1ᵢ₊₁ 字符和s2 ⱼ₊₁字符相同，则

dp[i+1][j+1]=dp[i][j]+1，如果s1ᵢ₊₁ 字符和s2 ⱼ₊₁字符不相同，则

dp[i+1][j+1]=Max（dp[i+1][j]，dp[i][j+1]）。可以查看下方s1和s2的dp[][]图。说到这里代码也就出来了

 3、代码

import java.util.Scanner;public class Main {public static int MaxLength(String s1, String s2) {int m = s1.length();int n = s2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (s1.charAt(i - 1) == s2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[m][n];}public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String s = sc.nextLine();String[] ss = s.split(" ");System.out.println(MaxLength(ss[0], ss[1]));}}
}

四、多写一题

最长公共子序列(二)_牛客题霸_牛客网 (nowcoder.com)

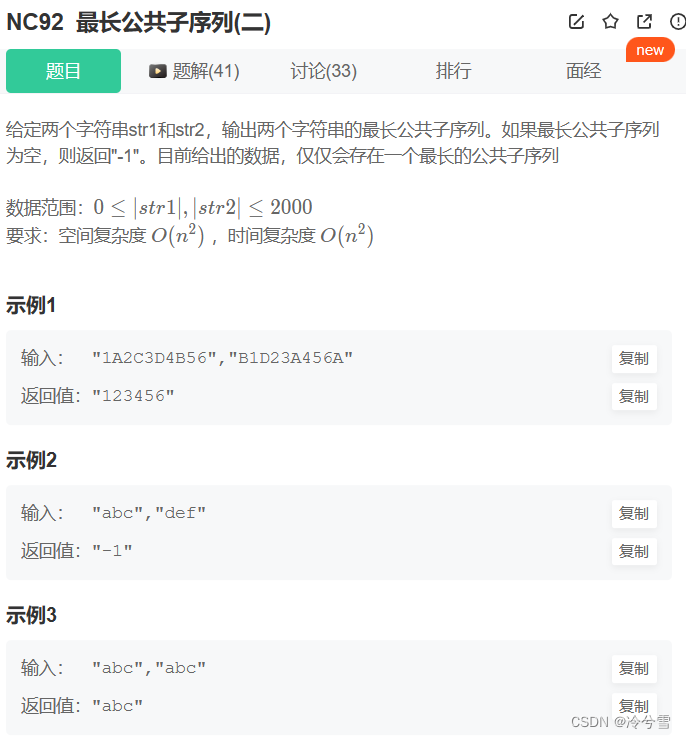
 这题和一一样创建一个数组保存s1和s2的LCS，只不过不一样的是，这次保存的是String，是字符串，思路都是一样的。可以看下面代码基本上没改什么。

import java.util.Scanner;public class 最长公共子序列2 {public static String LCS(String s1, String s2) {int m = s1.length();int n = s2.length();//int[][] dp = new int[m+1][n+1];String[][] s=new String[m+1][n+1];for (int i=0;i<=n;i++){s[0][i]=" ";}for (int i=0;i<=m;i++){s[i][0]=" ";}for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){if(s1.charAt(i - 1) == s2.charAt(j - 1)){//dp[i][j] = dp[i - 1][j - 1] + 1;s[i][j]=s[i-1][j-1].concat(String.valueOf(s1.charAt(i-1)));}else{//dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);s[i][j]=s[i-1][j].length()>s[i][j-1].length()?s[i-1][j]:s[i][j-1];}}}if (s[m][n].equals(" "))return "-1";return s[m][n].trim();}}

五、应用

最长公共子序列是一个十分实用的问题，它可以描述两段文字之间的“相似度”，即它们的雷同程度，从而能够用来辨别抄袭。对一段文字进行修改之后，计算改动前后文字的最长公共子序列，将除此子序列外的部分提取出来，这种方法判断修改的部分，往往十分准确。

二、最长上升子序列问题（LIS）

最长上升子序列问题是在一个无序的给定序列中找到一个尽可能长的由低到高排列的子序列，这种子序列不一定是连续的或者唯一的。

1、题目

最长上升子序列

 2、题目解读

题目要求我们求最长上升子序列的长度。还是先举一个例子271564389，可以很容易得出这个序列的各个数的最长上升子序列。我们还是思考dp[i]和dp[i-1]的关系，即当sᵢ >sᵢ₋₁时，

 dp[i]=Max(dp[i-1]+1,dp[i]），比如上面的6，在遍历到5之前dp[4]=2,遍历到5时dp[4]=dp[3]+1=3；dp[]数初始化为1，上面的1，前面没有比1小的数，所以还是1。当sᵢ<sᵢ₋₁时，就像上面的1一样，不用进行变化。

 3、代码

import java.util.Arrays;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {int n= sc.nextInt();int[] arr=new int[n];int[] dp=new int[n];//初始化数组都为1，表示第i个数本身Arrays.fill(dp,1);for (int i=0;i<n;i++){arr[i]=sc.nextInt();}int max=0;for(int i=0;i<n;i++){for(int j=0;j<i;j++){if(arr[j]<arr[i]&&dp[j]+1>dp[i])dp[i]=dp[j]+1;}max=Math.max(dp[i],max);}System.out.println(max);}}
}

四、多写一道

和唱队列

描述

N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学不交换位置就能排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1, 2, …, K，他们的身高分别为T1, T2, …, TK，则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1 <= i <= K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入

输入的第一行是一个整数N（2 <= N <= 100），表示同学的总数。第一行有n个整数，用空格分隔，第i个整数Ti（130 <= Ti <= 230）是第i位同学的身高（厘米）。

输出

输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。

样例输入

8
186 186 150 200 160 130 197 220

样例输出

4

 Ⅰ、题目解读

题目会给我们n个人的身高，要求我们找出要至少多少人出列这些人的身高才可以形成下面坡状（中间高两边矮）。

 这也是一个最长上升子序列问题，只不过前面的都是从左边向右边找，这次即要从左边向右边找也要从右边向左找，然后计算出哪个人的左子序列+右子序列-1最大（加了两次自己，所以要-1）。

 所以样例输出为8-5+1=4

 Ⅱ、代码

import java.util.Scanner;public class Main{public static void main(String[]args){Scanner sc=new Scanner(System.in);while(sc.hasNext()){int n=sc.nextInt();int[]num=new int[n];//存储n位同学的身高int []left=new int[n];//存储左侧最长递增子序列的元素个数int []right=new int[n];//存储右侧最长递增（从右向左看）子序列的元素个数for(int i=0;i<n;i++){num[i]=sc.nextInt();//对于每一个同学num[i]来说，左（右）侧最长递增子序列只有一个元素（就是本身）left[i]=1;right[i]=1;}//左子序列for(int i=0;i<n;i++)//固定某个学生num[i]不变{for(int j=0;j<i;j++)//依次遍历该学生左侧的每个学生{if(num[j]<num[i]&&left[j]+1>left[i])//当学生j的身高比学生i矮，并且满足递增性时，left[i]增加left[i]=left[j]+1;}}//右子序列//右侧与左侧同理for(int i=n-1;i>=0;i--){for(int j=n-1;j>i;j--){if(num[j]<num[i]&&right[j]+1>right[i])right[i]=right[j]+1;}}int max=0;//对于每个学生i而言，左侧最长递增序列元素个数和左侧最长递增序列元素个数和最大时该数目就是合唱队的最多人数+1for(int i=0;i<n;i++){if(left[i]+right[i]>max){max=left[i]+right[i];}}System.out.println(n-max+1);//由于被固定的学生i被数了两次（左侧和右侧各一次），所以+1}}
}