【数据结构入门】二叉树之堆的实现
文章目录
- 前言
- 一、树
- 1.1 树的概念
- 1.2 树的相关概念
- 二、二叉树
- 2.1 二叉树的概念
- 2.2 特殊的二叉树
- 2.3 二叉树的性质
- 三、堆
- 3.1 堆的概念
- 3.2 堆的性质
- 3.3 堆的存储
- 3.4 堆的实现
- 3.4.1 堆的初始化
- 3.4.2 堆的销毁
- 3.4.1 堆向上调整算法
- 3.4.2 堆向下调整算法
- 3.4.3 堆的创建
- 3.4.4 堆的插入
- 3.4.5 堆的删除
- 3.4.6 堆顶元素
- 3.4.7 判断堆是否为空
- 3.4.8 堆的元素个数
- 3.4.9 Heap.h
- 总结
前言
堆是一种重要的数据结构,常用于解决各种问题,如优先队列、排序算法、图算法等。堆具有很多特性,其中最常见的是最大堆和最小堆。最大堆中,每个节点的值都大于等于其子节点的值,而最小堆则相反,每个节点的值都小于等于其子节点的值。
在本文中,我们将详细介绍堆的概念、性质和操作。我们将以一个具体的例子来说明堆的构建和调整过程,并通过图示展示堆的结构。最后,我们还将讨论堆在实际应用中的一些常见用途和算法。通过学习堆,您将能够更好地理解和应用这一重要的数据结构。
要想理解堆,我们先需要知道树的概念,事实上堆是一种二叉树。
一、树
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关概念

结点的度:一个结点含有的子树的个数称为该结点的度; 如上图:A的为6
叶结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等结点为叶结点
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等结点为分支结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点(也就是亲兄弟结点)
树的度:一棵树中,最大的结点的度称为树的度; 如上图:树的度为6
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
二、二叉树
2.1 二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根结点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
1.二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:

2.2 特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 2 k − 1 2^k -1 2k−1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3 二叉树的性质
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2 ( i − 1 ) 2^{(i-1)} 2(i−1) 个结点.
- 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是 2 h − 1 2^h-1 2h−1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n 0 n_0 n0, 度为2的分支结点个数为 n 2 n_2 n2,则有 n 0 n_0 n0= n 2 n_2 n2+1
- 若规定根结点的层数为1,具有n个结点的满二叉树的深度,h= l o g 2 ( n + 1 ) log_2(n+1) log2(n+1). (ps: l o g 2 ( n + 1 ) log_2(n+1) log2(n+1)是log以2为底,n+1为对数)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置结点的双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
三、堆
3.1 堆的概念
如果有一个关键码的集合K = { k 0 k_0 k0, k 1 k_1 k1, k 2 k_2 k2,…, k n − 1 k_{n-1} kn−1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: K i K_i Ki <= K 2 ∗ i + 1 K_{2*i+1} K2∗i+1 且 K i K_i Ki<= K 2 ∗ i + 2 K_{2*i+2} K2∗i+2 ( K i K_i Ki >= K 2 ∗ i + 1 K_{2*i+1} K2∗i+1 且 K i K_i Ki >= K 2 ∗ i + 2 K_{2*i+2} K2∗i+2) i = 0,1,2…,则称为小堆(或大堆)。将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
3.2 堆的性质
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。

3.3 堆的存储
堆一般使用顺序结构的数组来存储,但是普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。堆作为一个完全二叉树是完全可以用数组来存储的,不会浪费太多空间。
3.4 堆的实现
3.4.1 堆的初始化
- assert 判空,防止野指针的出现
- 初始容量设为4
void HeapInit(HP* php)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType)*4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}
3.4.2 堆的销毁
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}
数组的销毁,比较简单
3.4.1 堆向上调整算法
基本思想:
向上调整算法有一个前提:左右子树必须是一个堆,才能调整。所以在建堆时,要建好大堆或者小堆。
具体步骤:
- 将新插入的元素放置在堆的最后一个位置(通常是数组的末尾)。
- 将该元素与其父节点进行比较。
- 若该元素大于(或小于,具体根据堆是最大堆还是最小堆而定)其父节点的值,则交换该元素和其父节点的位置。
- 继续向上对比和交换,直到满足堆的性质或达到堆的根节点。
void ADjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//不建议while(parent>=0) 因为parent到不了-1,但是也可以跑,因为后面if条件不满足while (child>0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
3.4.2 堆向下调整算法
向下调整算法与向上调整一样,但是它的时间复杂度比向上调整算法低:左右子树必须是一个堆,才能调整。所以在建堆时,要建好大堆或者小堆。
具体步骤:
- 从根结点开始向下调整。
- 将该元素与较小或较大的子节点进行比较。
- 若该元素大于(或小于,具体根据堆是最大堆还是最小堆而定)其子节点的值,则交换该元素和子节点的位置。
- 继续向下对比和交换,直到满足堆的性质或达到堆的叶节点。
void ADjustDown(HPDataType* a, int sz, int parent)
{int child = parent * 2 + 1;while (child < sz){//选出左右孩子中大的一个//这里child+1的判断在前,不要先访问再判断//这里a[child + 1] > a[child] 建大堆用>, 建小堆用<if (child + 1 < sz && a[child + 1] < a[child]){//这地方可能会越界++child;}//这里a[child] > a[parent] 建大堆用>, 建小堆用<if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
3.4.3 堆的创建
向下调整建堆
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void HeapInitArray(HP* php, int* a, int n)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = n;//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){ADjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);ADjustDown(a, end, 0);--end;}
}
3.4.4 堆的插入
判断容量不够时需要扩容,空间够,则插入后需要向上调整
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;ADjustUp(php->a, php->size - 1);
}
3.4.5 堆的删除
堆的删除要从堆顶开始删除,删除时先将堆顶元素与堆底元素进行交换,然后去掉堆底元素(也就是删掉了堆顶元素),然后再进行向下调整,保证堆的结构依旧满足。
这里从堆顶开始删除才有意义,堆顶的数据依次会是最大值(大堆)或者最小值(小堆)。
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size-1]);php->size--;ADjustDown(php->a, php->size, 0);
}
3.4.6 堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}
3.4.7 判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
3.4.8 堆的元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
3.4.9 Heap.h
#pragma oncetypedef int HPDataType;#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapDestory(HP* php);
void HeapInitArray(HP* php, int* a, int n);void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);
void Swap(HPDataType* p1, HPDataType* p2);void ADjustUp(HPDataType* a, int child);
void ADjustDown(HPDataType* a, int sz, int parent);
总结
堆的主要优点之一是能够在O(log n)的时间复杂度内找到最值,例如最大堆可以在常数时间内找到最大值。这使得堆可以在动态数据集合中高效地插入和删除元素。另外,堆还能够在排序算法中扮演重要角色,例如堆排序可以在O(n log n)的时间复杂度内对数据进行排序。
相关文章:

【数据结构入门】二叉树之堆的实现
文章目录 前言一、树1.1 树的概念1.2 树的相关概念 二、二叉树2.1 二叉树的概念2.2 特殊的二叉树2.3 二叉树的性质 三、堆3.1 堆的概念3.2 堆的性质3.3 堆的存储3.4 堆的实现3.4.1 堆的初始化3.4.2 堆的销毁3.4.1 堆向上调整算法3.4.2 堆向下调整算法3.4.3 堆的创建3.4.4 堆的插…...
智能微气候:精准调控背后的算法革命
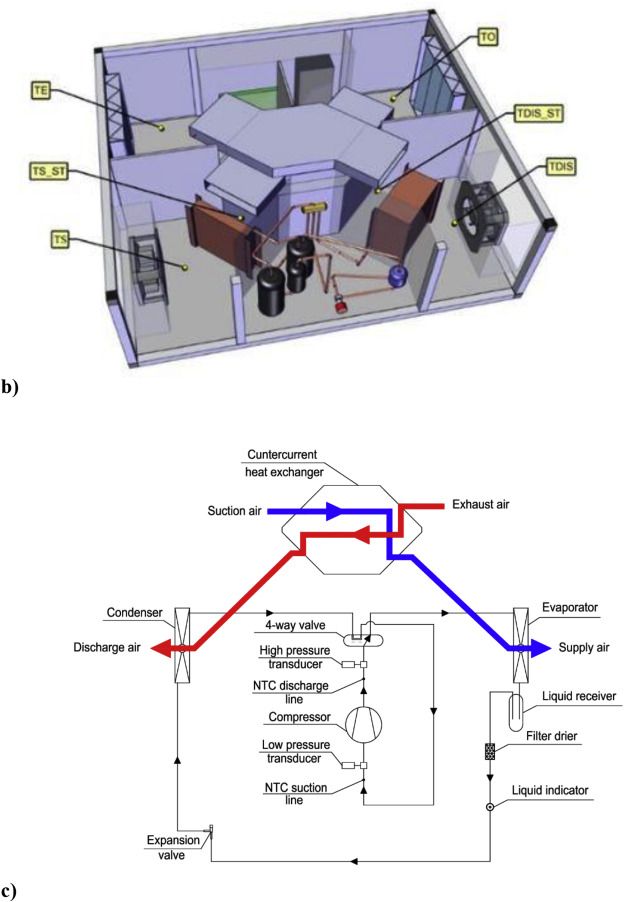
( 于景鑫 国家农业信息化工程技术研究中心)当人工智能遇见现代农业,会擦出怎样的火花?随着数字农业、智慧农业的蓬勃发展,人工智能技术正以前所未有的速度渗透到农业生产的方方面面。其中,以深度学习为代表的前沿算法,尤其是大语言模型(LLM),正在成为驱…...

eNSP 华为交换机链路聚合
华为交换机链路聚合 链路聚合好处: 1、提高带宽 2、链路冗余 SW_2: <Huawei>sys [Huawei]sys SW_2 [SW_2]vlan batch 10 20 [SW_2]int g0/0/4 [SW_2-GigabitEthernet0/0/4]port link-type access [SW_2-GigabitEthernet0/0/4]port default vl…...

编译器揭秘
从上世纪50年代开始,编程语言五花八门,编译器和解释器层出不穷。此处只列出常见编程语言的编译器和解释器信息,不常见的编程语言有单独文章介绍。 C/C cc 此处代表Unix C编译器,其他平台可能借用cc软链接到真正的C编译器。MSVC 微…...

ubuntu下qt连接mysql出现 QMYSQL driver not loaded
1、首先检查是否重新安装了MySQL的驱动,可以使用命令: sudo apt-get remove libqt5sql5-mysql sudo apt-get install libqt5sql5-mysql 2、重新安装ibmysqlclient-dev即可解决 sudo apt-get remove libmysqlclient-dev sudo apt-get install libmysq…...

html 首行缩进2字符
1. html 首行缩进2字符 1.1. 场景 在Html开发中让一段文字(富文本等)首行缩进两个文字,可能在前面加上8个“ ”,因为过去对CSS不熟悉,这种方法实现虽然比较直接,但是文字多的时候会有很多“ ”充斥在代码中…...

什么是IP?
目录 简介 IP IP协议 IP地址 发展历程 IP地址类型 公有地址 私有地址 IP地址编址方式 A类IP地址 B类IP地址 C类IP地址 D类IP地址 特殊的网址 子网 超网 无类间路由 IP地址的分配 IP地址管理 手工管理模式 DHCP分配IP地址的管理模式 通过交换机管理IP 地址…...

js拖拽交换元素位置
摘要:最近在做会议系统,9宫格小画面要支持拖拽调整顺序,需求已经实现了,简单记录下当时的逻辑处理。 /* 关于拖拽逻辑处理 start */ // 当前在拖动的下标 const curDragIndex useRef<number>(-1); /* 拖拽元素事件* onDragStart_开始* onDragend_结束 */ const handleD…...

在 C++ 中实现自定义容器的实用指南
在 C 中实现自定义容器的实用指南 在 C 编程中,容器是存储和管理数据的基本工具。标准库提供了多种容器,如 std::vector、std::list 和 std::map,但在某些情况下,开发者可能需要实现自定义容器以满足特定需求。本文将详细介绍如何…...

《深入浅出WPF》读书笔记.4名称空间详解
《深入浅出WPF》读书笔记.4名称空间详解 背景 主要讲明名称空间概念,可以理解为命名空间的引用。 xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml" 👆如x可以理解为一些列命名空间的引用。 不一一列举,只讲几个特殊的…...

电驱动总成
电驱动总成(Electric Drive Assembly)是电动汽车和混合动力汽车中关键的组成部分,主要负责将电能转化为机械能,以驱动汽车的轮胎。电驱动总成包括多个关键组件,通常可以分为以下几个主要部分: ### 主要组成…...

JavaScript class和正则
正则表达式练习 出生日期 年 月 日 ()表示一个整体 console.log(1909.match(^19\\d{2}$)); console.log(2024.match(^20(([01][0-9])|(2[0-4]))$)); //年 console.log(1909.match(^(19\\d{2})|(20(([01][0-9])|(2[0-4])))$)); // 月 console.log(12.match(^(0[1-9])|(1[0-2])…...
[Linux#42][线程] 锁的接口 | 原理 | 封装与运用 | 线程安全
互斥量 mutex • 大部分情况,线程使用的数据都是局部变量,变量的地址空间在线程栈空间 内,这种情况,变量归属单个线程,其他线程无法获得这种变量。 • 但有时候,很多变量都需要在线程间共享,这…...

奇异递归Template有啥奇的?
如果一个模版看起来很头痛,那么大概率这种模版是用来炫技,没啥用的,但是CRTP这个模版,虽然看起来头大,但是却经常被端上桌~ 奇异递归模板模式(Curiously Recurring Template Pattern, CRTP)是一…...

每天五分钟深度学习框架pytorch:神经网络工具箱nn的介绍
本文重点 我们前面一章学习了自动求导,这很有用,但是在实际使用中我们基本不会使用,因为这个技术过于底层,我们接下来将学习pytorch中的nn模块,它是构建于autograd之上的神经网络模块,也就是说我们使用pytorch封装好的神经网络层,它自动会具有求导的功能,也就是说这部…...

【办公软件】安全风险 Microsoft 已阻止宏运行,因为此文件的来源不受信任
Excel 2019版本,就出现安全风险 Microsoft 已阻止宏运行 因为此文件的来源不受信任的问题,宏直接就用不了了。 网上的解决方法,文件右键属性->取消安全锁。但存在没有安全锁这个选项。后查询到一个简单的解决方法。 打开Excel表格->文件…...

JavaScript语法基础之流程结构(顺序、选择、循环结构)
目录 1. 流程控制 1.1. 流程控制简介 1.1.1. 顺序结构 1.1.2. 选择结构 1.1.3. 循环结构 1.2. 选择结构:if 1.2.1. 单向选择:if… 1.2.2. 双向选择:if…else… 1.2.3. 多向选择:if…else_if…else… 1.3. 选择结构&#…...

集团数字化转型方案(四)
集团数字化转型方案通过全面部署人工智能(AI)、大数据分析、云计算和物联网(IoT)技术,创建了一个智能化的企业运营平台,涵盖从业务流程自动化、实时数据监控、精准决策支持,到个性化客户服务和高…...

【MySQL索引】索引失效场景
索引失效 1 全值匹配肯定不失效 2 最佳左前缀法则 索引文件具有 B-Tree 的最左前缀匹配特性,如果左边的值未确定,那么无法使用此索引。 3 主键插入顺序 页分裂,建议 让主键具有 AUTO_INCREMENT 4 计算、函数、类型转换(自动或手动)导致…...

基于MATLAB视觉的静态手势识别系统
一、课题介绍及思路 为了丰富手势识别方法的多样性,提高手势识别的正确率,提出了一种基于手势轮廓像素变化的手势识别方法。在Matlab环境下,设计并开发了一个基于视觉的静态手势识别系统。系统主要由两部分组成:手势分割与手势识…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

RFID推动新能源汽车零部件生产系统管理应用案例
RFID推动新能源汽车零部件生产系统管理应用案例 一、项目背景 新能源汽车零部件场景 在新能源汽车零部件生产领域,电子冷却水泵等关键部件的装配溯源需求日益增长。传统 RFID 溯源方案采用 “网关 RFID 读写头” 模式,存在单点位单独头溯源、网关布线…...


