博弈论,CF 1600E - Array Game
目录
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
二、解题报告
1、思路分析
2、复杂度
3、代码详解
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
| 1600E - Array Game |
二、解题报告
1、思路分析
记最长递增前缀长度为L,最长递减后缀长度为R
必胜态:L R 一奇一偶 或者 二者均奇
否则为必败态
证明:
先考虑一侧,比如递增前缀,如果L是偶数,那么我们先手在左侧拿,后手一定也能在左侧拿
如果一直保持左侧拿,先手就输了
如果LR都是偶数,那么就算先手前后来回换,我们一定会走到一侧没法拿另一侧为偶数,然后输掉游戏,因此 LR都是偶数为必败态
若L,R一奇一偶,那么先手拿奇,后手就落入了必败态
若L,R二者均奇,那么我们拿第一个元素大的那个,就会使得一侧不能拿,后手会落入必败态
2、复杂度
时间复杂度: O(N)空间复杂度:O(N)
3、代码详解
#include <bits/stdc++.h>
#include <ranges>using i64 = long long;
using i32 = unsigned int;
using u64 = unsigned long long;
using i128 = __int128;constexpr int inf32 = 1E9 + 7;
constexpr i64 inf64 = 1E18 + 7;
constexpr int P = 1'000'000'007;void solve() {int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; ++ i) std::cin >> a[i];int L = 0, R = 0;for (int i = 0; i < n; ++ i)if (!i || a[i] > a[i - 1])++ L;elsebreak;for (int i = n - 1; ~i; -- i)if (i + 1 == n || a[i] > a[i + 1])++ R;elsebreak;if (((L + R) & 1) || ((L & 1) && (R & 1)))std::cout << "Alice";elsestd::cout << "Bob";
}auto FIO = []{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);return 0;
}();int main () {#ifdef DEBUGfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);#endifint T = 1;// std::cin >> T;while (T --)solve();return 0;
}相关文章:

博弈论,CF 1600E - Array Game
目录 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 1600E - Array Game 二、解题报告 1、思路分析 记最长递增前缀长度为L&a…...

win10安装docker,打包python、java然后centos执行镜像
一、win10安装Docker Desktop docker官网(需要魔法)下载:https://www.docker.com/products/docker-desktop/ 安装方法参考:https://blog.csdn.net/beautifulmemory/article/details/137970794 下载完毕后界面安装,不勾…...

【数据结构入门】二叉树之堆的实现
文章目录 前言一、树1.1 树的概念1.2 树的相关概念 二、二叉树2.1 二叉树的概念2.2 特殊的二叉树2.3 二叉树的性质 三、堆3.1 堆的概念3.2 堆的性质3.3 堆的存储3.4 堆的实现3.4.1 堆的初始化3.4.2 堆的销毁3.4.1 堆向上调整算法3.4.2 堆向下调整算法3.4.3 堆的创建3.4.4 堆的插…...
智能微气候:精准调控背后的算法革命
( 于景鑫 国家农业信息化工程技术研究中心)当人工智能遇见现代农业,会擦出怎样的火花?随着数字农业、智慧农业的蓬勃发展,人工智能技术正以前所未有的速度渗透到农业生产的方方面面。其中,以深度学习为代表的前沿算法,尤其是大语言模型(LLM),正在成为驱…...

eNSP 华为交换机链路聚合
华为交换机链路聚合 链路聚合好处: 1、提高带宽 2、链路冗余 SW_2: <Huawei>sys [Huawei]sys SW_2 [SW_2]vlan batch 10 20 [SW_2]int g0/0/4 [SW_2-GigabitEthernet0/0/4]port link-type access [SW_2-GigabitEthernet0/0/4]port default vl…...

编译器揭秘
从上世纪50年代开始,编程语言五花八门,编译器和解释器层出不穷。此处只列出常见编程语言的编译器和解释器信息,不常见的编程语言有单独文章介绍。 C/C cc 此处代表Unix C编译器,其他平台可能借用cc软链接到真正的C编译器。MSVC 微…...

ubuntu下qt连接mysql出现 QMYSQL driver not loaded
1、首先检查是否重新安装了MySQL的驱动,可以使用命令: sudo apt-get remove libqt5sql5-mysql sudo apt-get install libqt5sql5-mysql 2、重新安装ibmysqlclient-dev即可解决 sudo apt-get remove libmysqlclient-dev sudo apt-get install libmysq…...

html 首行缩进2字符
1. html 首行缩进2字符 1.1. 场景 在Html开发中让一段文字(富文本等)首行缩进两个文字,可能在前面加上8个“ ”,因为过去对CSS不熟悉,这种方法实现虽然比较直接,但是文字多的时候会有很多“ ”充斥在代码中…...

什么是IP?
目录 简介 IP IP协议 IP地址 发展历程 IP地址类型 公有地址 私有地址 IP地址编址方式 A类IP地址 B类IP地址 C类IP地址 D类IP地址 特殊的网址 子网 超网 无类间路由 IP地址的分配 IP地址管理 手工管理模式 DHCP分配IP地址的管理模式 通过交换机管理IP 地址…...

js拖拽交换元素位置
摘要:最近在做会议系统,9宫格小画面要支持拖拽调整顺序,需求已经实现了,简单记录下当时的逻辑处理。 /* 关于拖拽逻辑处理 start */ // 当前在拖动的下标 const curDragIndex useRef<number>(-1); /* 拖拽元素事件* onDragStart_开始* onDragend_结束 */ const handleD…...

在 C++ 中实现自定义容器的实用指南
在 C 中实现自定义容器的实用指南 在 C 编程中,容器是存储和管理数据的基本工具。标准库提供了多种容器,如 std::vector、std::list 和 std::map,但在某些情况下,开发者可能需要实现自定义容器以满足特定需求。本文将详细介绍如何…...

《深入浅出WPF》读书笔记.4名称空间详解
《深入浅出WPF》读书笔记.4名称空间详解 背景 主要讲明名称空间概念,可以理解为命名空间的引用。 xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml" 👆如x可以理解为一些列命名空间的引用。 不一一列举,只讲几个特殊的…...

电驱动总成
电驱动总成(Electric Drive Assembly)是电动汽车和混合动力汽车中关键的组成部分,主要负责将电能转化为机械能,以驱动汽车的轮胎。电驱动总成包括多个关键组件,通常可以分为以下几个主要部分: ### 主要组成…...

JavaScript class和正则
正则表达式练习 出生日期 年 月 日 ()表示一个整体 console.log(1909.match(^19\\d{2}$)); console.log(2024.match(^20(([01][0-9])|(2[0-4]))$)); //年 console.log(1909.match(^(19\\d{2})|(20(([01][0-9])|(2[0-4])))$)); // 月 console.log(12.match(^(0[1-9])|(1[0-2])…...
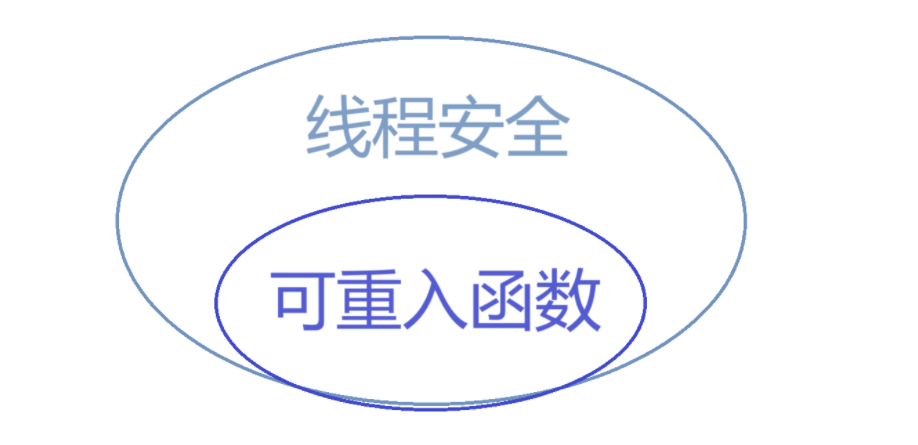
[Linux#42][线程] 锁的接口 | 原理 | 封装与运用 | 线程安全
互斥量 mutex • 大部分情况,线程使用的数据都是局部变量,变量的地址空间在线程栈空间 内,这种情况,变量归属单个线程,其他线程无法获得这种变量。 • 但有时候,很多变量都需要在线程间共享,这…...

奇异递归Template有啥奇的?
如果一个模版看起来很头痛,那么大概率这种模版是用来炫技,没啥用的,但是CRTP这个模版,虽然看起来头大,但是却经常被端上桌~ 奇异递归模板模式(Curiously Recurring Template Pattern, CRTP)是一…...

每天五分钟深度学习框架pytorch:神经网络工具箱nn的介绍
本文重点 我们前面一章学习了自动求导,这很有用,但是在实际使用中我们基本不会使用,因为这个技术过于底层,我们接下来将学习pytorch中的nn模块,它是构建于autograd之上的神经网络模块,也就是说我们使用pytorch封装好的神经网络层,它自动会具有求导的功能,也就是说这部…...

【办公软件】安全风险 Microsoft 已阻止宏运行,因为此文件的来源不受信任
Excel 2019版本,就出现安全风险 Microsoft 已阻止宏运行 因为此文件的来源不受信任的问题,宏直接就用不了了。 网上的解决方法,文件右键属性->取消安全锁。但存在没有安全锁这个选项。后查询到一个简单的解决方法。 打开Excel表格->文件…...

JavaScript语法基础之流程结构(顺序、选择、循环结构)
目录 1. 流程控制 1.1. 流程控制简介 1.1.1. 顺序结构 1.1.2. 选择结构 1.1.3. 循环结构 1.2. 选择结构:if 1.2.1. 单向选择:if… 1.2.2. 双向选择:if…else… 1.2.3. 多向选择:if…else_if…else… 1.3. 选择结构&#…...

集团数字化转型方案(四)
集团数字化转型方案通过全面部署人工智能(AI)、大数据分析、云计算和物联网(IoT)技术,创建了一个智能化的企业运营平台,涵盖从业务流程自动化、实时数据监控、精准决策支持,到个性化客户服务和高…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...


