NC 完全二叉树结点数
系列文章目录
文章目录
- 系列文章目录
- 前言
前言
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧。

描述
给定一棵完全二叉树的头节点head,返回这棵树的节点个数。
完全二叉树指:设二叉树的深度为h,则 [1,h-1] 层的节点数都满足 个
个

class Solution {
public:int nodeNum(struct TreeNode* head) {if (!head) return 0; // 空树算0个// 计算左右孩子, 不用判空, 如果left或right为空, 函数返回0int lh = getHeight(head->left), rh = getHeight(head->right);int res = 1; // 根节点算1个if (lh == rh) {// (1<<lh) - 1 是左子树满二叉树的节点数, 右子树一定也是完全二叉树, 故递归计算res += nodeNum(head->right) + (1<<lh) - 1;} else {// 同上, 右子树一定是满二叉树res += nodeNum(head->left) + (1<<rh) - 1;}return res;}int getHeight(struct TreeNode* head) {int h = 0; // 初始高度是0while (head) {h++; // 当前节点存在, 高度加1head = head->left; // 向左走}return h;}
};
相关文章:

NC 完全二叉树结点数
系列文章目录 文章目录 系列文章目录前言 前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧。 描述 给定一棵完全…...

点灯案例优化(二) 利用位运算修改特定位
前面,我们对点灯代码进行了第一次优化,效果如下 尽管第一次优化以后代码可读性确实高了不少,也看起来更加简洁,但是,这里仍旧存在一个很严重的问题:就在每一个表达式右边,我们给寄存器的数据赋值…...

【C++备忘录】
记录一些C比较好用的代码块,方便自个查看。 使用std::copy 快速打印序列 #include <iostream> #include <algorithm> #include <iterator>int main() {int a[5] { 1, 2, 3, 4, 5 };copy(begin(a), end(a), ostream_iterator<int>(cout, …...

java编程 斐波拉契数列算法集锦【斐波拉契数列】【下】【集合类】【Stream函数式编程】
斐波那契数列(Fibonacci sequence),又称黄金分割数列,是一个非常经典的递归问题。斐波那契数列的算法描述: 斐波那契数列,一个令人着迷而又充满神秘色彩的数字序列,它以0和1作为起始ÿ…...

智慧园区三维可视化平台
背景 随着物联网、人工智能等新一代信息技术的发展,数字孪生技术逐渐成为实现这一目标的关键工具。数字孪生技术能够对物理世界进行高精度、全要素的映射,并实时动态反映其变化情况,从而为园区提供精准的管理和服务。 方案简介 智慧园区数字…...

Redis 有序集合【实现排行榜】
使用 Redis 的 Sorted Set 数据结构可以非常高效地实现实时排行榜功能。Sorted Set 允许将元素按分数进行排序,同时支持插入、删除和查询操作,且这些操作的时间复杂度较低,非常适合处理高并发的场景。 实现思路 插入操作:当用户…...

ORACLE数据库管理系统介绍
1.ORACLE的特点: 可移植性 ORACLE采用C语言开发而成,故产品与硬件和操作系统具有很强的独立性。从大型机到微机上都可运行ORACLE的产品。可在UNIX、DOS、Windows等操作系统上运行。可兼容性 由于采用了国际标准的数据查询语言SQL,与IBM的SQL/DS、DB2等均兼容。并提供读取其它…...

C# 中Linq探讨 Or条件拼接
在C#中,没有直接内置于.NET Core或.NET Framework中的NuGet包能够直接“拼接”LINQ的OR条件,因为LINQ本身设计为一种声明式编程模型,用于查询数据集合。然而,你可以通过一些方式来实现多个条件以OR逻辑组合的效果,而不…...

有关应用层面试题有关库的思维导体
面试题目: TCP通信中3次握手和四次挥手? 答: 第一次握手:客户端发送SYN包(SYN1, seq0)给服务器,并进入SYN_SENT状态,等待服务器返回确认包。第二次握手:服务器接收到S…...

记一次 SAP BP 编号范围错误引发的一个问题 GET_NRIV_LINE
本来想着循着错误提示去排查,但是还是想看看业务发生了什么,他们的操作是否有问题,不经意间发现 号码段是有问题的,由此大概可以判断是他们编号范围和类型之间的问题 角色和分组是否一致的,如果不一致就发生了以上错误…...

(17)ELK大型储存库的搭建
前言: els是大型数据储存体系,类似于一种分片式存储方式。elasticsearch有强大的查询功能,基于java开发的工具,结合logstash收集工具,收集数据。kibana图形化展示数据,可以很好在大量的消息中准确的找到符…...
)
每日一问:Kafka消息丢失与堆积问题分析(简化版)
Kafka 消息系统问题解析 在本篇博客中,我们将深入探讨 Kafka 中常见的两大问题:消息丢失和消息堆积。首先,我们将简要介绍 Kafka 的基本工作原理,随后分别分析消息丢失和堆积的原因,并提供针对性的解决方案。 关于其详…...

C语言中函数sizeof和strlen区别
sizeof和strlen是C语言中的两个常用函数,它们的作用和使用方式有所不同。 sizeof sizeof是一个运算符而非函数,用于计算数据类型或变量占用的字节数。它可以计算任意数据类型(包括基本类型、自定义结构体、数组等)的大小。例如&…...
---- Python + MinIO + Kafka进阶)
RAG与LLM原理及实践(14)---- Python + MinIO + Kafka进阶
目录 背景 根因分析 配置 构造 创建 network 构造 zookeeper 构造 kafka 参数构造 原理解析 图解 全过程解析 工具使用 kafkacat 查看 broker python 实现 python send + kafka recv python 代码 kafka recv 运行效果 python recv + kafka send python 代…...

接口自动化-代码实现
接口自动化基础 1、接口自动化测试 接口自动化:使用工具或代码代替人对接口进行测试的技术测试目的: 防止开发修改代码时引入新的问题测试时机: 开发进行系统测试转测前,可以先进行接口自动化脚本的编写开发进行系统测试转测后&…...

如何查看linux大文件
文章目录 一、查看存储情况二、查看指定路径下的文件大小查看临时文件和日志的大小 三、查找home目录下文件大小大于100M的大文件四、查看INNODE使用情况五、查看进程使用情况查看所有进程查看特定进程杀死相关进程 六、清除缓存操作七、 查看docker的硬盘占用情况详细查看 一、…...

生成式人工智能服务大模型备案答疑
问:大模型备案范围 答:利用生成式人工智能技术向中华人民共和国境内公众提供生成文本、图片、音频、视频等内容的服务,适用本办法。 未向境内公众提供生成式人工智能服务的,不适用本办法的规定。 ps:生成式人工智能…...
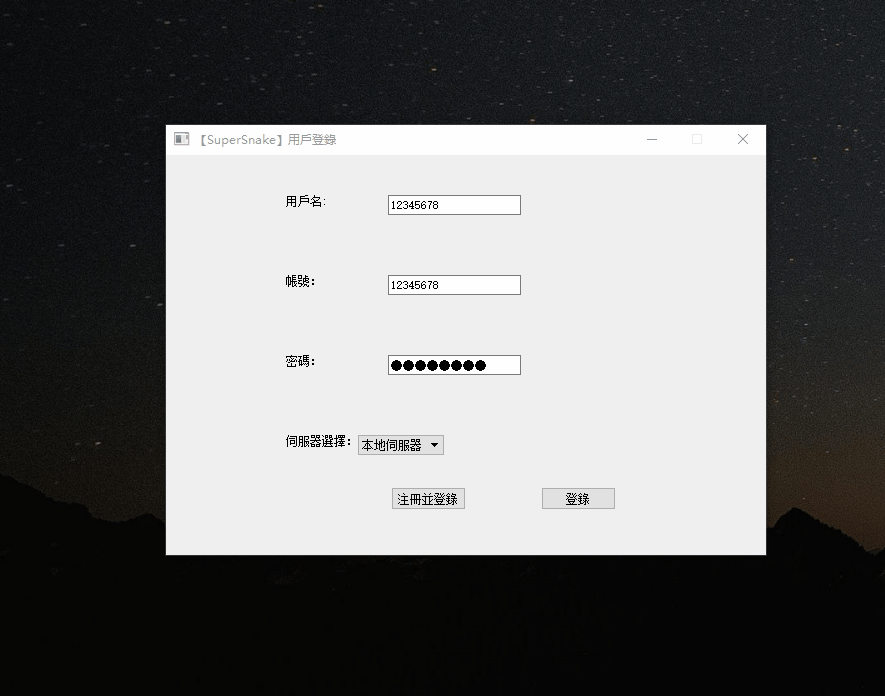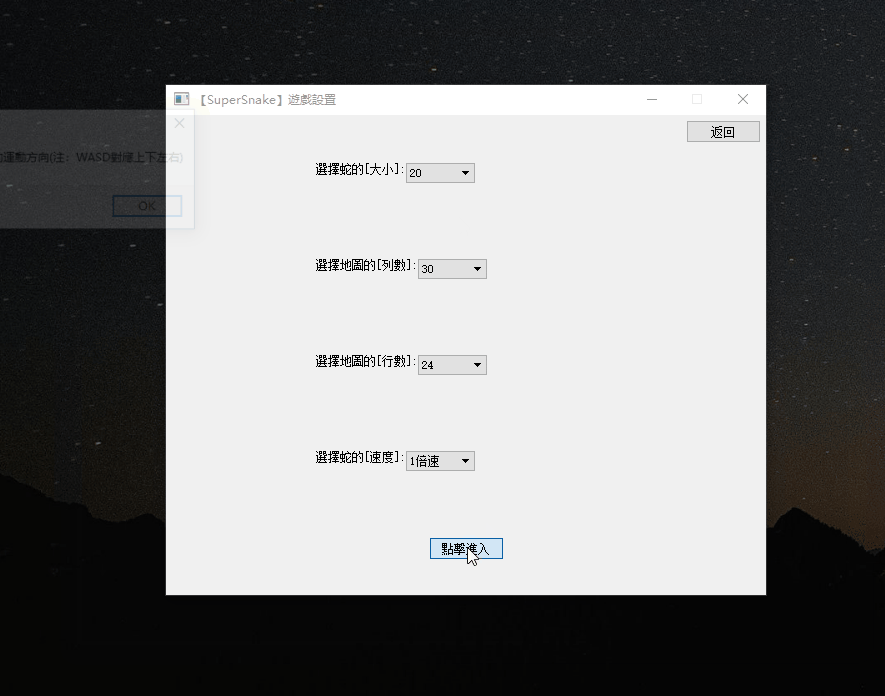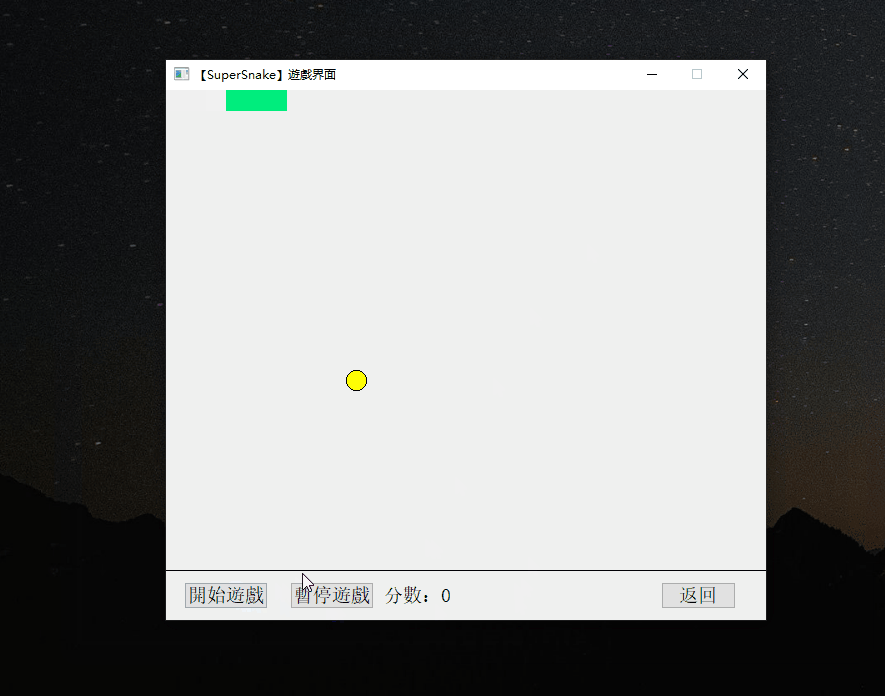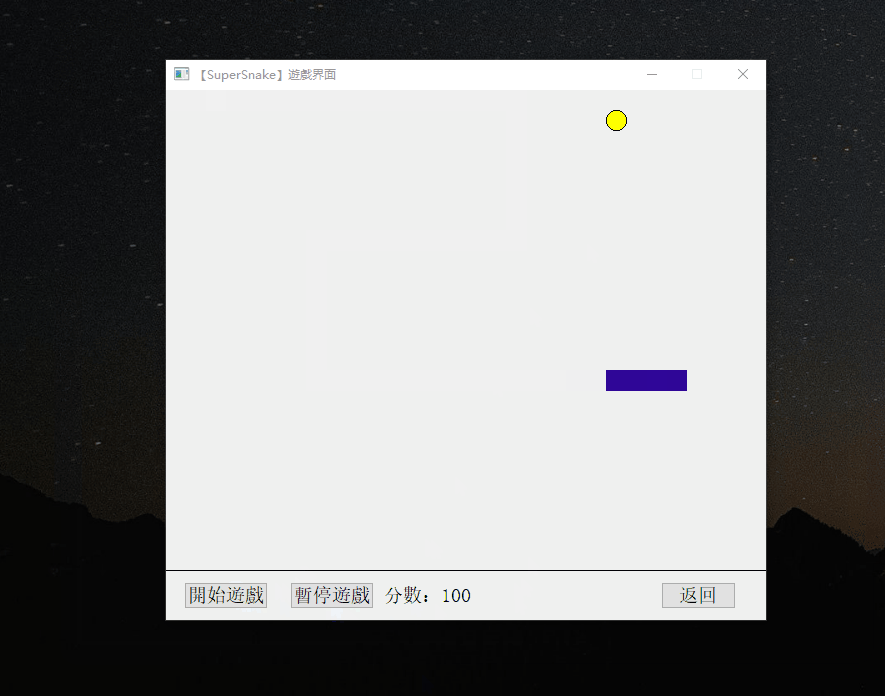
QT-贪吃蛇小游戏
QT-贪吃蛇小游戏 一、演示效果二、核心代码三、下载链接 一、演示效果 二、核心代码 #include "Food.h" #include <QTime> #include <time.h> #include "Snake.h"Food::Food(int foodSize):foodSize(foodSize) {coordinate.x -1;coordinate.…...

虚幻5|AI视力系统,听力系统,预测系统(1)视力系统
继宠物伴随系统初步篇后续 虚幻5|AI巡逻宠物伴随及定点巡逻—初步篇-CSDN博客 一,听力系统 1.打开宠物ai的角色蓝图 2.选中ai感知组件 右侧细节,找到ai感知,添加感知配置,我们需要的是ai视力配置 3.选中左侧创建的ai感知组件&…...

IC rankIC
IC IC衡量的是预测值和实际值之间的相关系数 计算公式为:IC Pearson(R(predicted),R(actual)) 取值范围:[-1, 1],其中1表示完全相关,也就是预测值和实际值完全一样。0表示完全不相关,-1表示,反向相关 ra…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
