机器学习|正则化|评估方法|分类模型性能评价指标|吴恩达学习笔记
前文回顾:逻辑回归
目录
📚正则化
🐇过拟合的问题
🐇代价函数
🐇正则化线性回归
🐇正则化的逻辑回归模型
📚模型评估方法
🐇留出法(hold-out)
🐇交叉验证法(cross-validation)
🐇自助法(bootstrap)
🐇比较总结
📚分类模型性能评价指标
🐇混淆矩阵
🐇准确度(Accuracy)
🐇精确度(precision)和召回率(Recall,TPR)
🐇精确度和召回率的调和平均(F_score)
🐇假阳性率(FPR)和真阴性率(TFR)
🐇ROC曲线与AUC的值
🐇PR曲线(Precision-recall Curve)
🐇ROC曲线与PR曲线的关系
📚正则化
🐇过拟合的问题
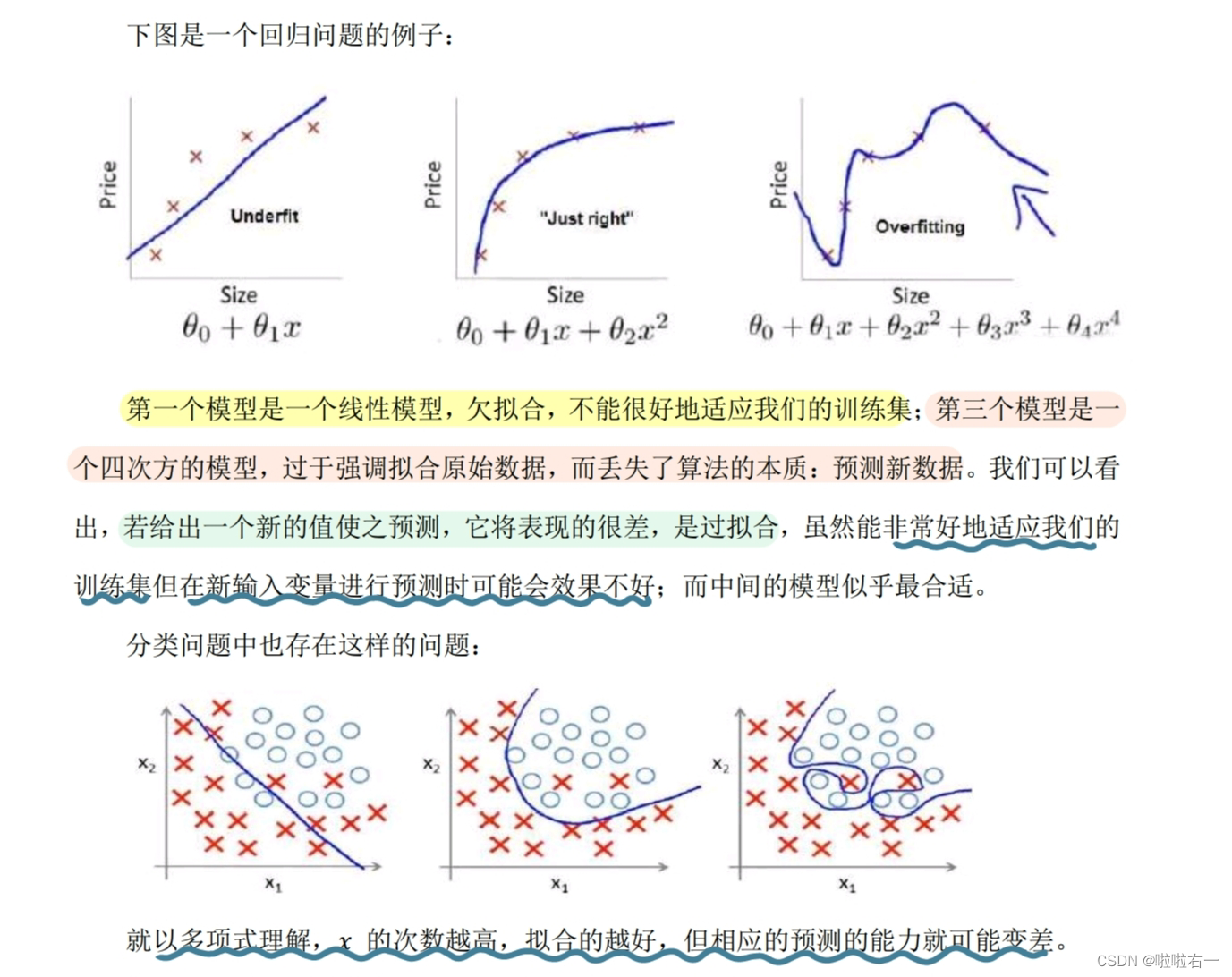
🌟如何处理过拟合问题?
- 丢弃一些不能帮我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙。
- 正则化。保留所有的特征,但是减少参数的大小。
🐇代价函数

🐇正则化线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。

🐇正则化的逻辑回归模型

以上参考学习链接:【中英字幕】吴恩达机器学习系列课程,以上对应7.1-7.4
📚模型评估方法
关于测试集与训练集:
- 将训练集类比为模拟试卷,将测试集类比为正式考试试卷。
- 测试集要尽可能地与训练集互斥(即测试样本尽量不在训练集中出现),显然,正式考试的题在模拟卷里做过,会影响测试结果。
- 测试集和训练集的划分要尽可能地保持数据分布的一致性(避免因数据划分过程中引入额外的偏差而对最终结果产生影响),显然,只有模拟卷的题型和正式考试的题型差不多,刷模拟卷的效果才更好。
🐇留出法(hold-out)
留出法是直接将数据集D划分为两个互斥的集合,其中一个作为训练集S,另一个作为测试集T。模型是从训练集归纳出来的,性能是在测试集上进行评估。

为了保持训练集和测试集数据分布一致,避免额外的误差,我们可以采用分层随机抽样(分层采样),从而保持相同的类分布。
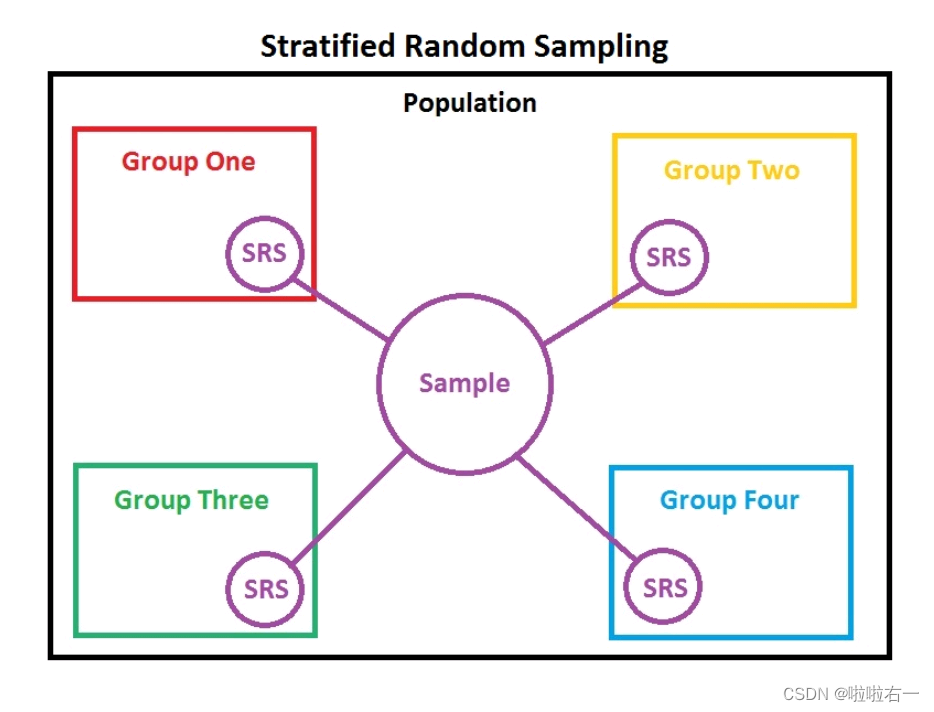
假设数据集D:1000,其中训练集S(70%),测试集T(30%)。若数据集D包含500正例,500反例,那么最终采样的结果是训练集有350正例,350反例,测试集有150正例,150反例。
留出法具有较高的方差。T的评估可能在很大程度上取决于哪些数据点最终出现在训练集中,哪些数据点最终出现在测试集中。且可用于训练的样本较少,因为有些样本被保留用于测试。因此,单独使用留出法得到的估计结果往往不够稳定可靠。为提高性能,在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。

依然存在的限制:
- 留出法没有尽可能多地利用数据进行训练
- 它也无法控制每条记录用于测试和训练的次数
🐇交叉验证法(cross-validation)
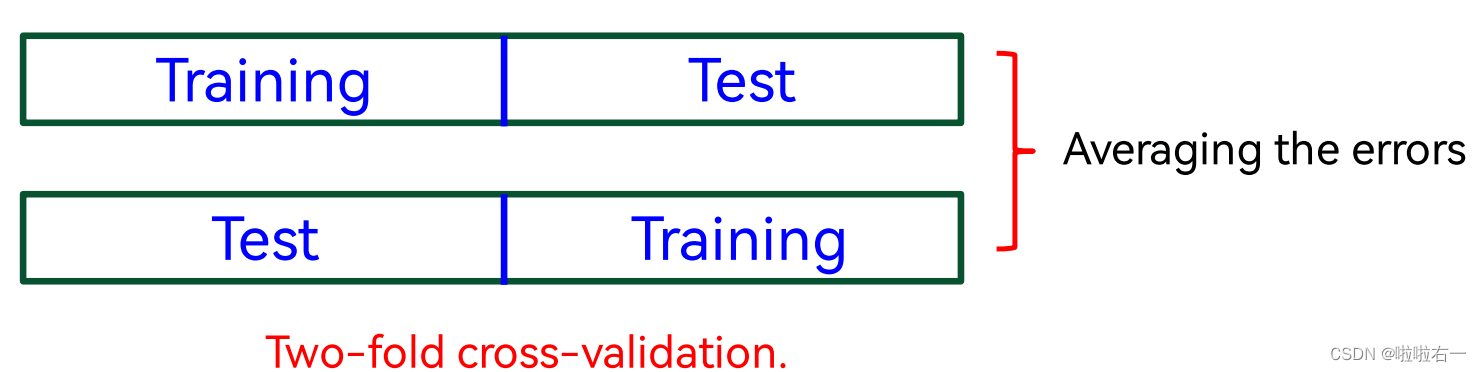
最简单的交叉验证(2折交叉):假设我们把数据分成两个大小相等的子集,我们选择其中一个子集进行训练,另一个进行测试。然后我们交换子集的角色,使之前的训练集称为测试集,反之亦然。最后总误差是通过对两次运行的误差求平均得到。
一般地,k折交叉验证是将数据分成k个大小相等的分区,在每次运行过程中,选择一个分区进行测试,而其余分区则用于训练。这个过程重复k次,以便每个分区恰好用于测试一次。总误差是通过对所有k次运行的误差进行平均得到的。类似于留出法,k折交叉法同样可以重复几次。
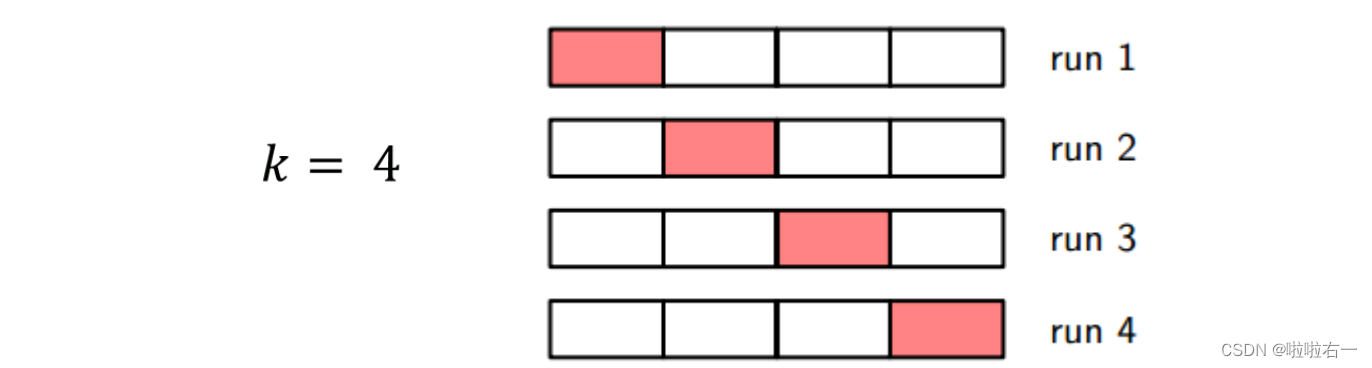
k折交叉法的一种特殊情况:设置k=N(即数据集的大小),这就是所谓的留一法(leave-out-out)。每个测试集只包含一条记录。留一法不受划分方式的影响,每个样本都是一个分区。留一法的评估结果往往被认为是比较准确的,不过当数据集比较大的时候,训练m个模型的计算开销难以承受。
🐇自助法(bootstrap)
在自助法中,训练集被替换采样,即已经选择用于训练的数据被返回原始数据集,这样它被重新选中的概率和原来相等。平均而言,一个大小为N的自举样本包含原始数据集中约63.2%的数据。
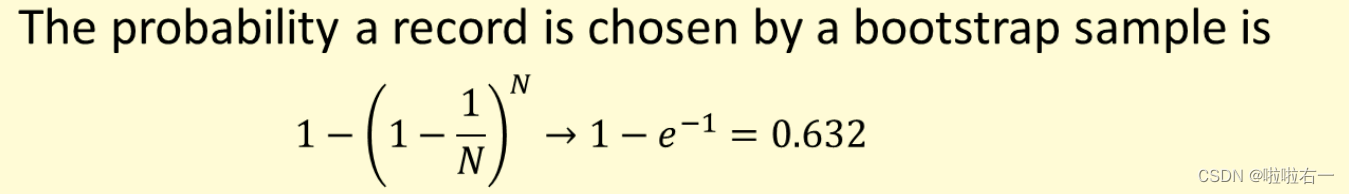
没有包含在自举样本中的数据作为测试集。
假设数据集D有N个样本,通过抽取返回的方式从数据集D中抽取N个样本,这抽取出的N个样本就是D'。数据集D中有部分样本从来没有被抽到过,那么没被抽到过的这些数据集就作为测试集D-D',训练集为D'。
自助法可以从相同的原始数据集生成许多不同的训练集,这使得它在数据集小、难以有效划分训练/测试集时很有用。但自助法会改变初始数据集的分布,会引入估计偏差。因此,如果我们有足够的数据,留出法和交叉验证法将被更广泛地使用。
🐇比较总结
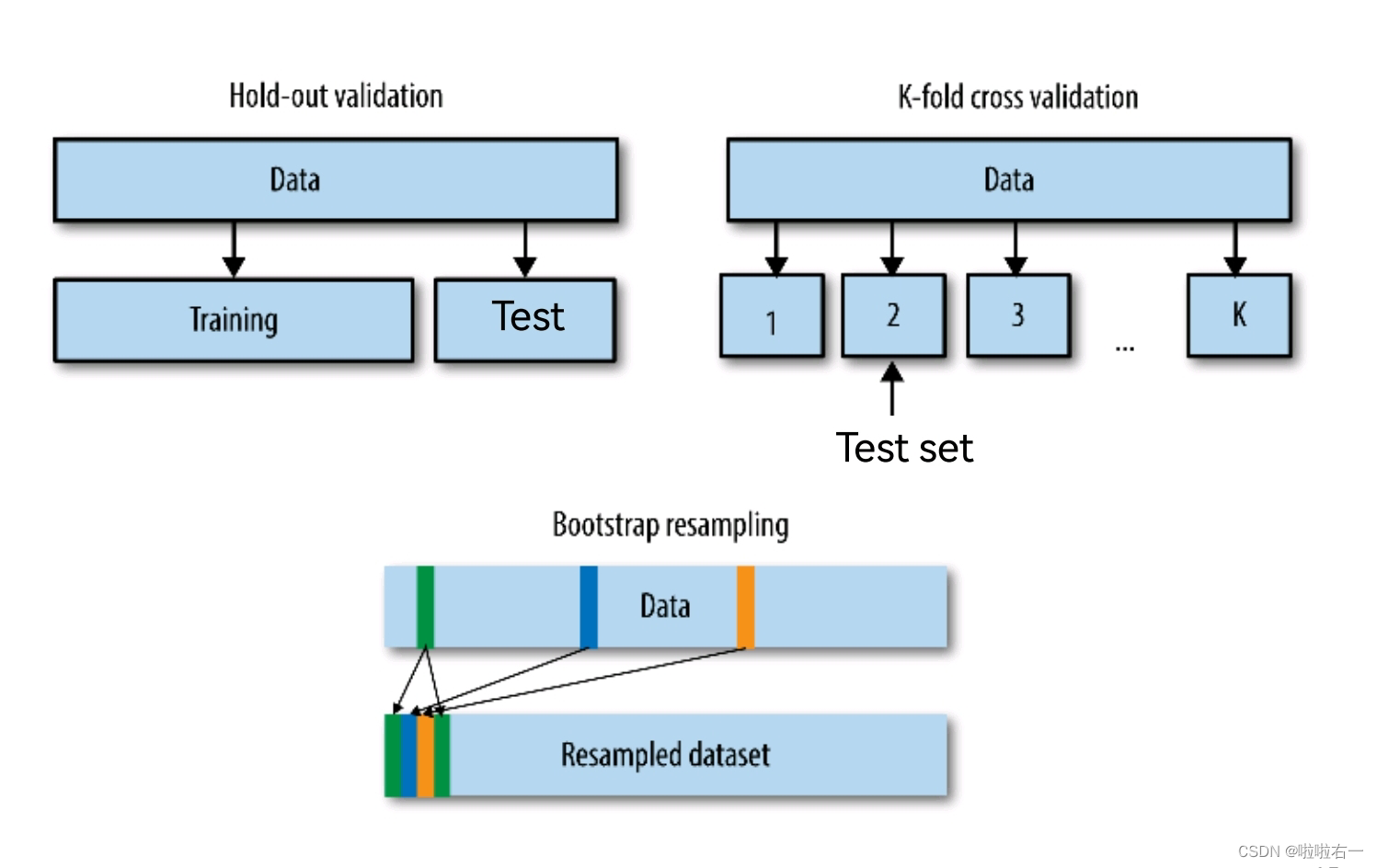
📚分类模型性能评价指标
🐇混淆矩阵
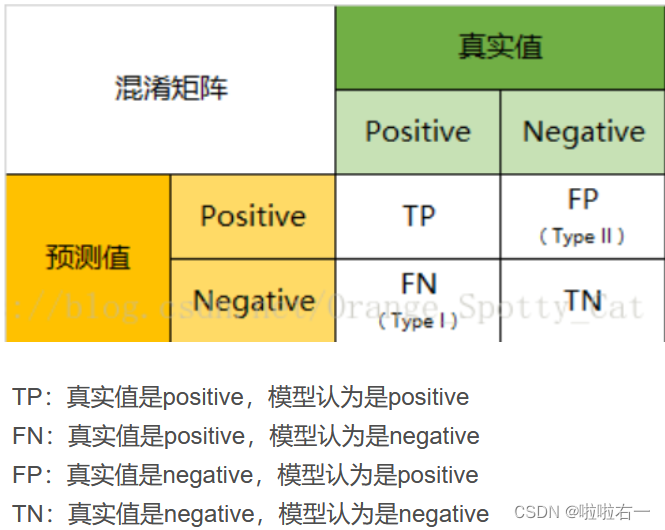
🐇准确度(Accuracy)
对于给定的测试集,模型正确分类的样本数与总样本数之比。
 更高的准确性并不一定意味着在目标任务上有更好的表现(偏向多数类),它的隐含假设是例子之间的类分布是相对平衡的。
更高的准确性并不一定意味着在目标任务上有更好的表现(偏向多数类),它的隐含假设是例子之间的类分布是相对平衡的。
考虑一个二元分类例子:0类示例的数量为9990,1类的数量为10,如果预测全部为0,那准确率也有9990/10000=99.9%,但这显然不正确。
🐇精确度(precision)和召回率(Recall,TPR)
| 精确度 | 召回率 |
| 对于给定测试集,分类模型将正类样本预测为正类的数量与将样本预测为正类的综述的比例。 | 对于给定测试集,模型将正类样本分为正类的数量与模型分类正确的数量的比值。 |
| TP / (TP+FP) | TP / (TP+FN) |

一般来说,精确度和召回率是相互矛盾的衡量标准,Recall↑ → Precision↓,反之亦然,why?
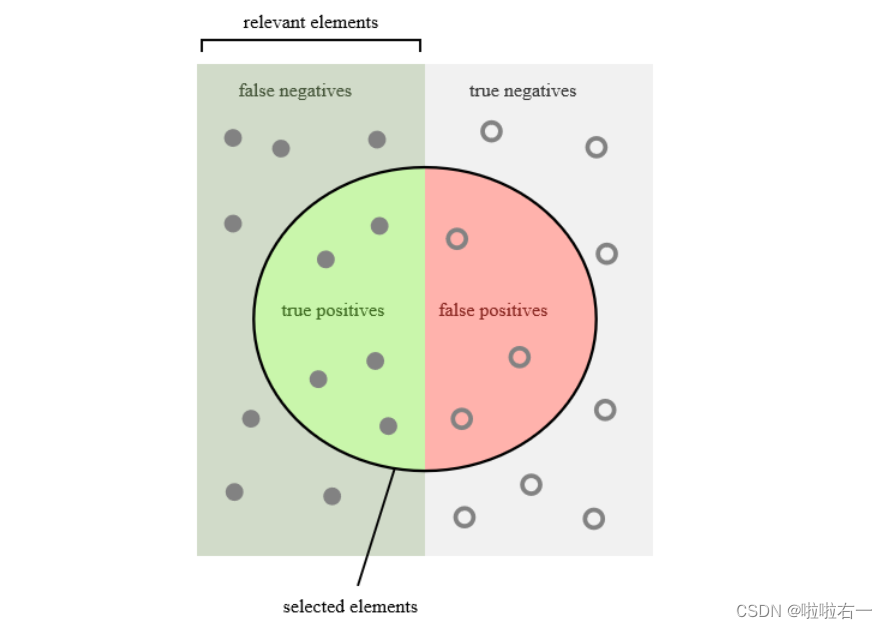
在信息检索中,我们可以认为:
- TP = 实际相关的检索文档
- FP = 实际不相关的检索文档
- TN = 实际不相关的未检索文档
- FN = 实际相关的未检索文档
为了尽可能多地检索相关文档(增加查全率),我们尽可能多地检索文档。最极端的情况是所有的文档都会被检索到,其中所有相关的文档肯定都会被检索到(Recall =1)。然而,精度会相当低。Recall↑ → Precision↓
为了提高精度,我们只检索置信度高的文档,但这样难免会遗漏一些相关的文档,降低查全率。即有Precision↑ → Recall↓
🐇精确度和召回率的调和平均(F_score)
该指标用来综合的衡量模型的召回率和精确度,β是权重因子,当β=1,即为F1_score。
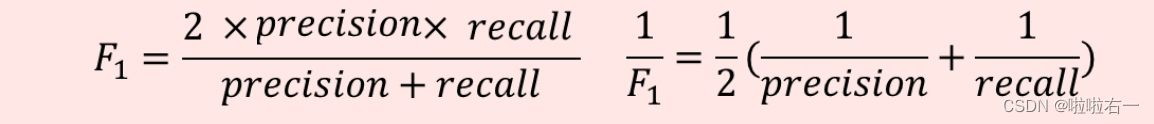

有时我们可能有多个混淆矩阵:重复训练几次;在多个数据集上进行训练;多类或多标签
我们如何评价多类分类的精度和召回率?

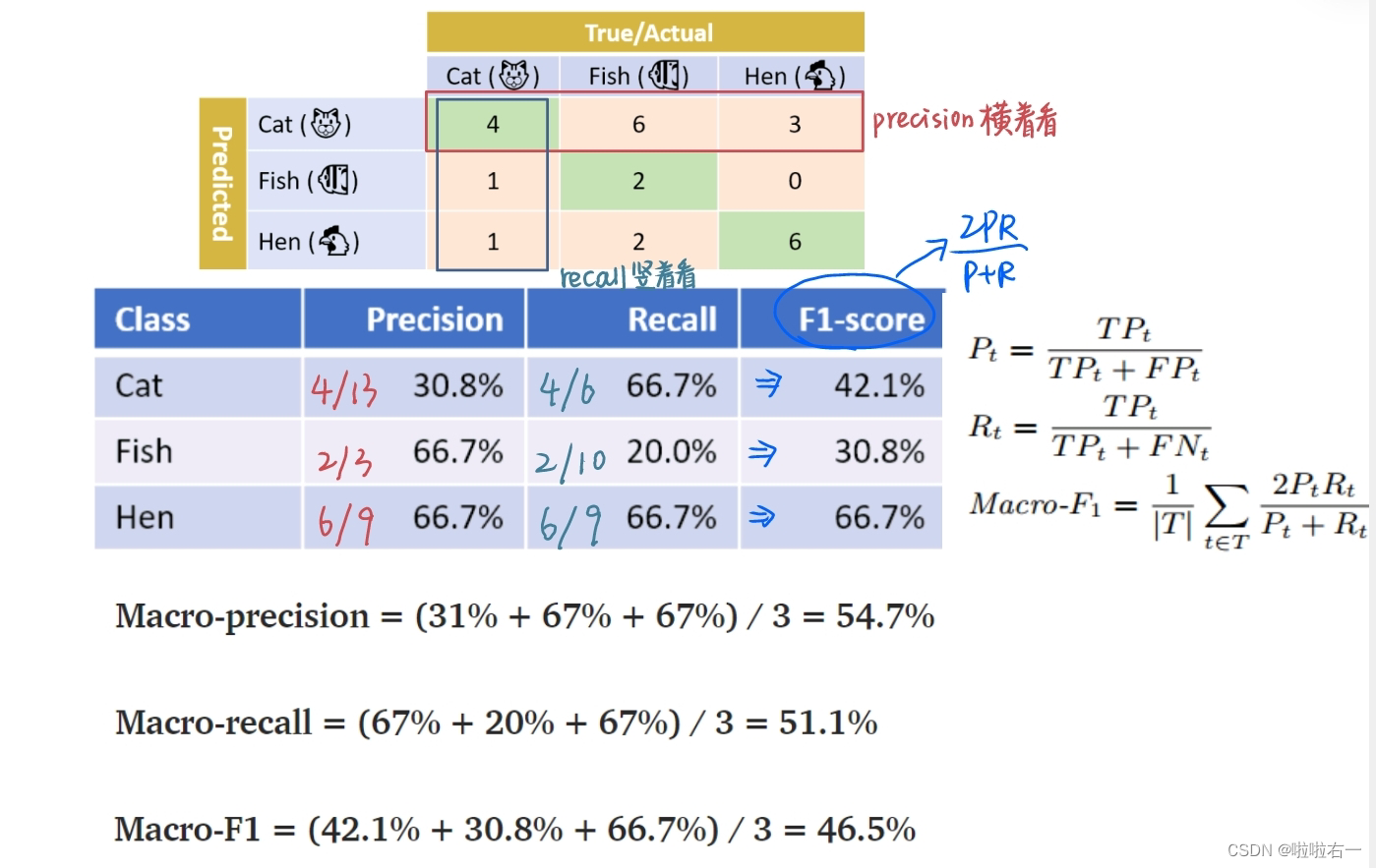
假设我们有一组照片。每张照片显示一种动物:猫、鱼或母鸡。我们的分类器需要预测每张照片中显示的是哪种动物。
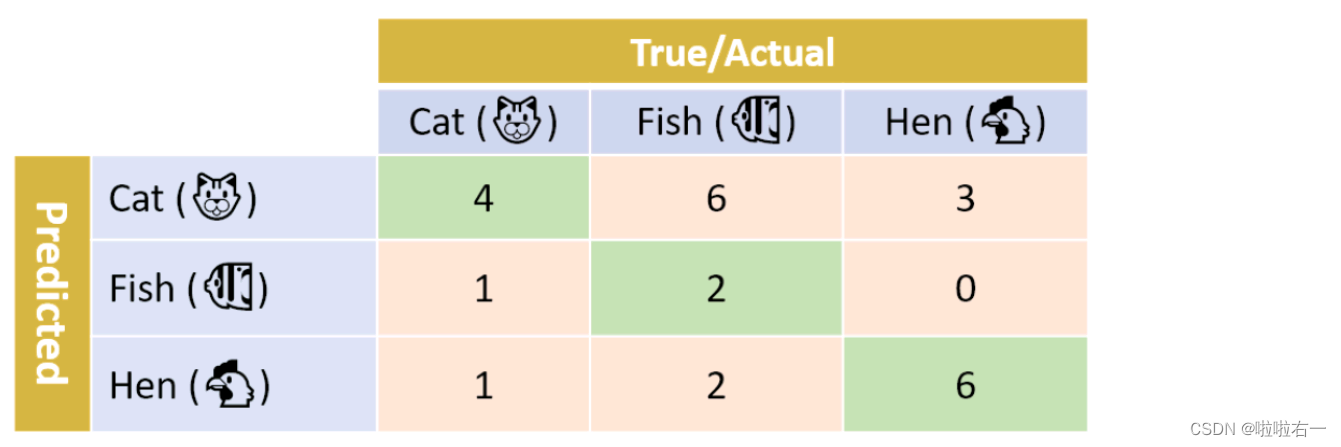
宏查准率、宏查全率和宏F1
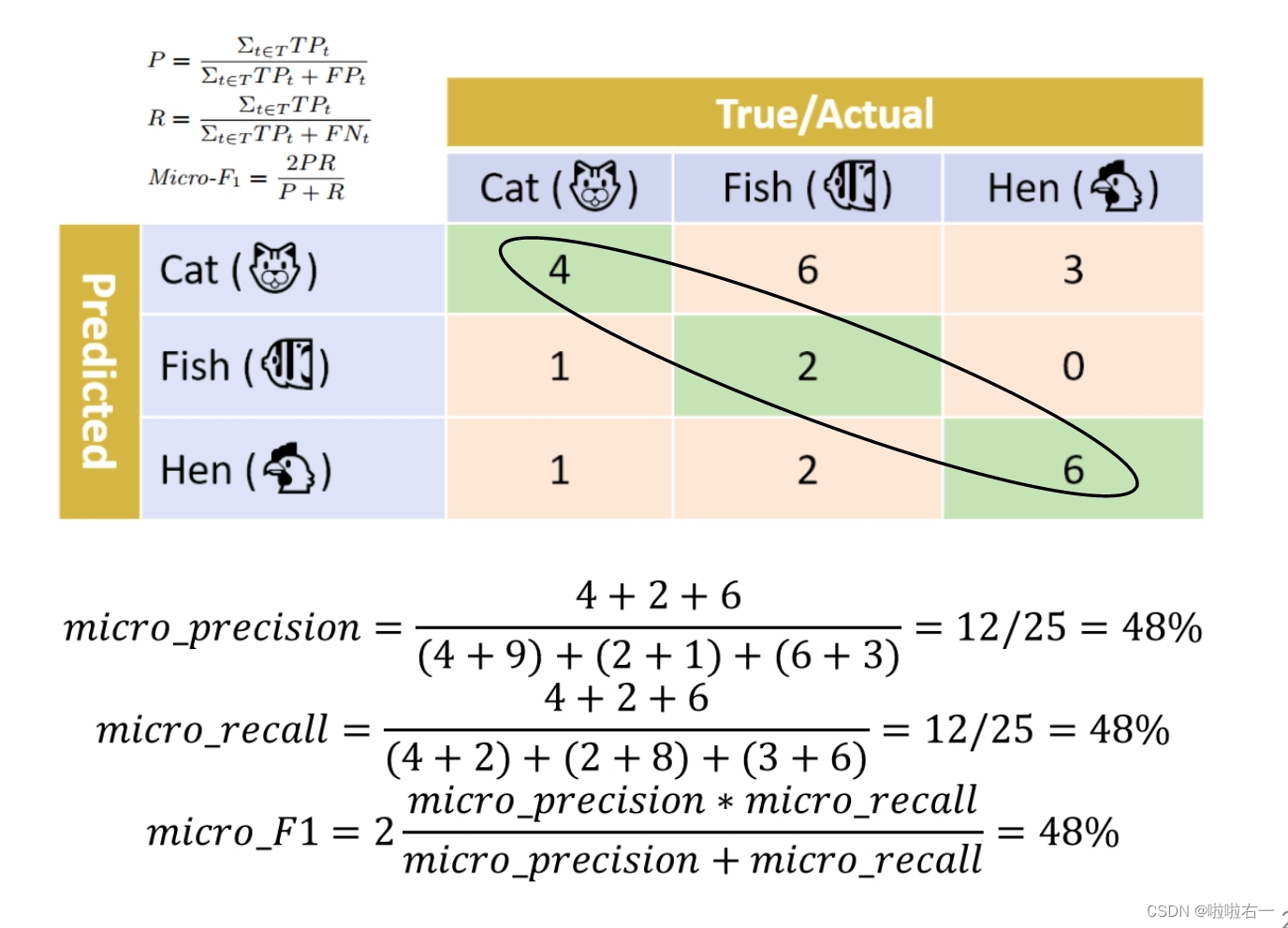
微查准率、微查全率和微F1
🐇假阳性率(FPR)和真阴性率(TFR)

🐇ROC曲线与AUC的值
ROC曲线是衡量分类器性能的一种常见方法。ROC曲线的实际意义在于评估分类器在不同阈值下的真阳性率和假阳性率,以达到最优的分类效果。ROC曲线下面积越接近1,从图中看曲线越接近左上角,说明分类器的性能越好。ROC曲线下面积的值即为AUC值。
设置不同的阈值可以得到不同的混淆矩阵,而每个混淆矩阵又会对应一个TPR、FPR值,在图中对应得到一个点,改变不同的阈值,得到不同的点,最终画出该分类器对应的ROC曲线。
关于分类器阈值以及ROC曲线的实际含义解释,推荐观看该哔哩哔哩视频
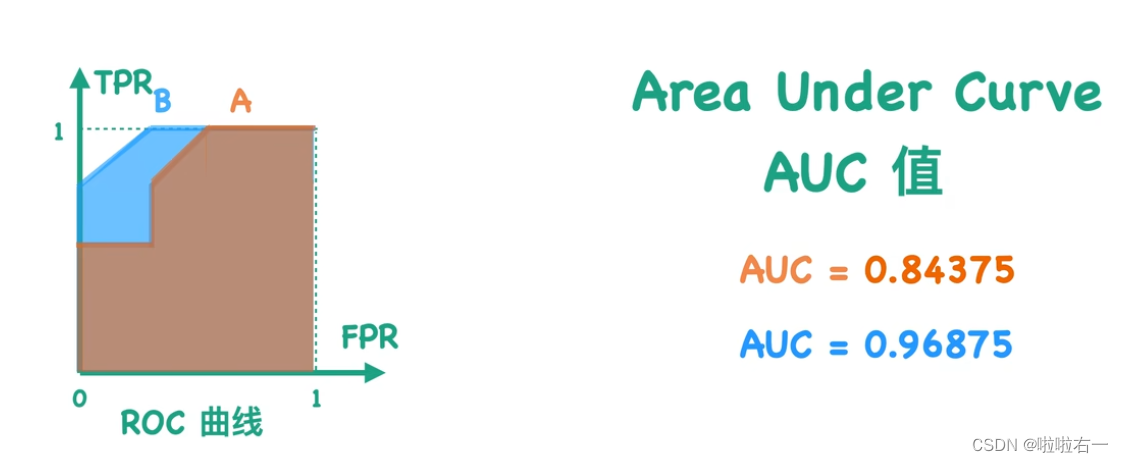
- 横坐标为假阳性率——FPR = FP / (TN+FP)
- 纵坐标为真阳性率——TPR = TP / (TP+FN)
🐇PR曲线(Precision-recall Curve)
Precision-Recall Curve可以反映分类器在不同的查全率和查准率条件下的性能表现,评估分类器在不同阈值下的查全率和查准率。通常来说,我们希望分类器在保证尽可能高的查准率的基础上,能够达到较高的查全率。因此,我们可以通过对比不同分类器在同一数据集上的Precision-Recall Curve来选择最优的分类器。曲线越接近右上角,表示分类器的性能越好。

- 横坐标为查全率(召回率,Recall,TPR)——TP / (TP+FN)
- 纵坐标为查准率(精确度,Precision)——TP / (TP+FP)
其中,召回率是指所有真实正样本中被分类器成功预测为正样本的比例,而精确度则是指所有被分类器成功预测为正样本的样本中真正正样本的比例。(详见上文)
🐇ROC曲线与PR曲线的关系
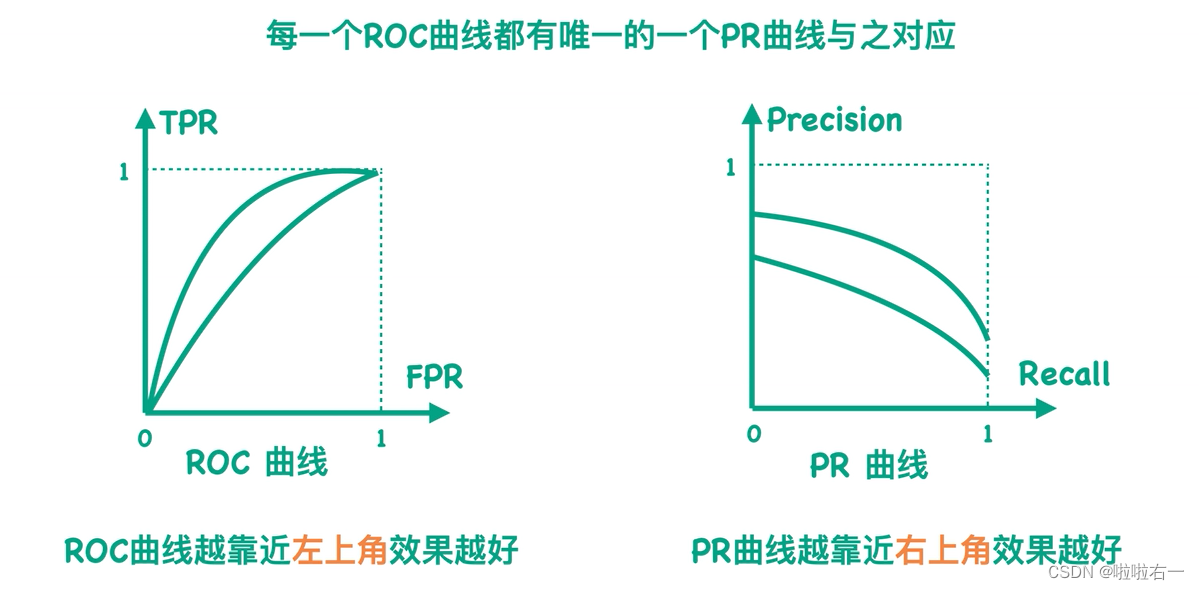
每一个ROC曲线都有唯一的一个PR曲线与之对应,并且如下图,ROC曲线中在左边的那条线对应PR中在上方的那条线。
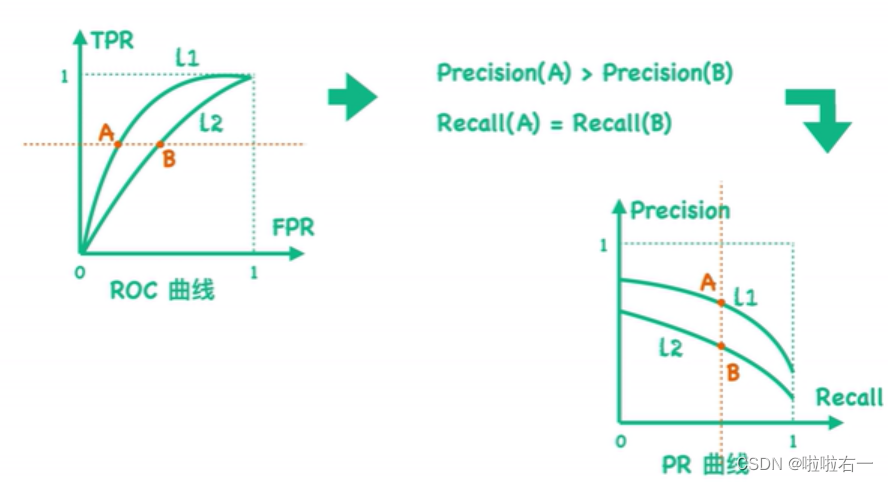
ROC曲线与PR曲线的适用场景
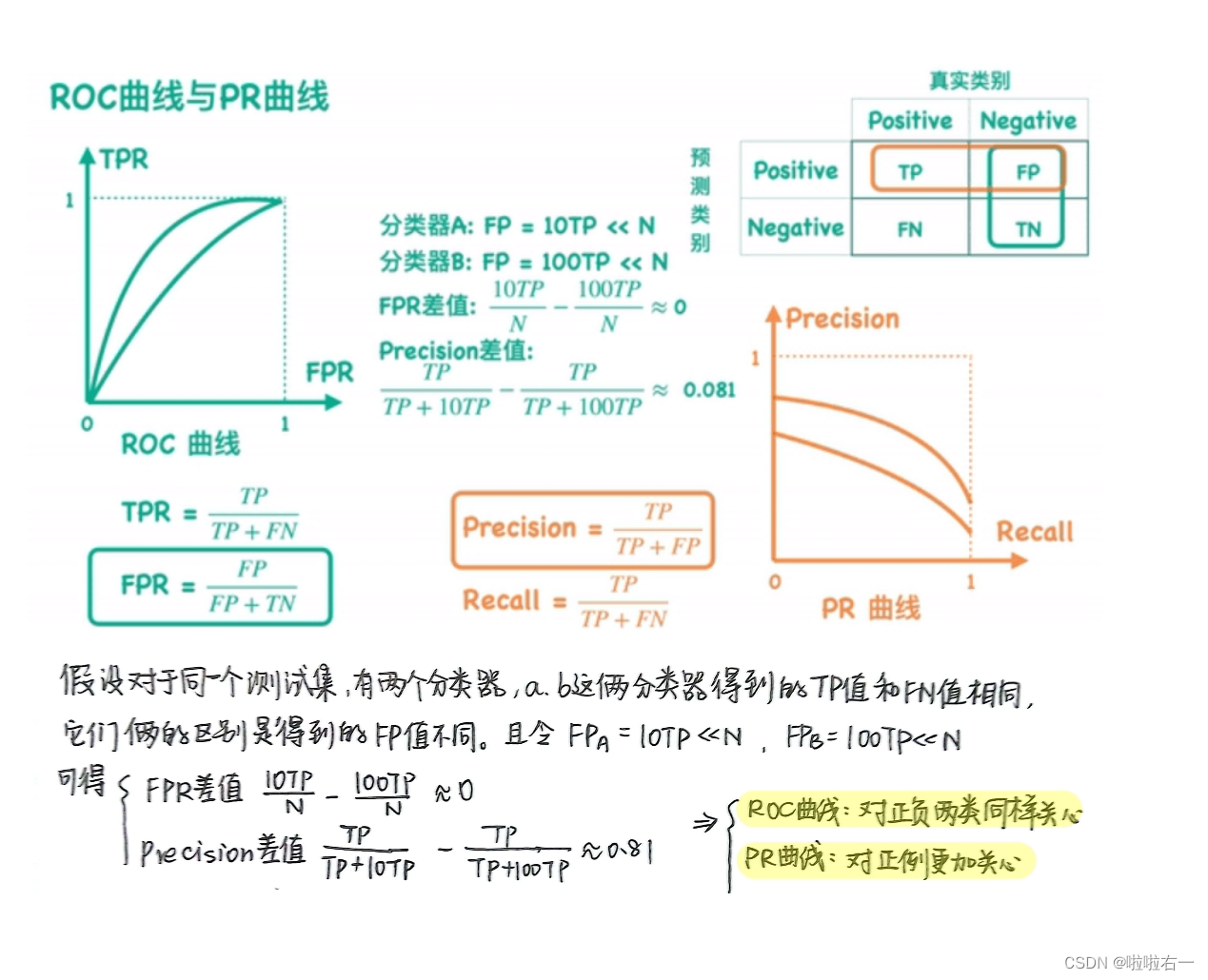
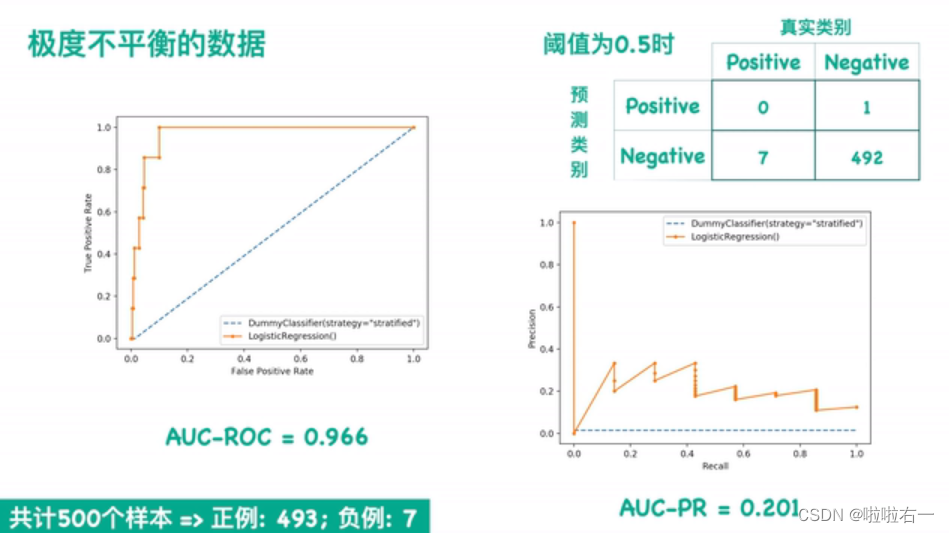
以下是一个直观的极度不平衡的例子
- 我们可以很明显地看出右边这个图效果是很差的(越靠近右上角的越好),而左边这个图它感觉这个模型效果还是很好的。
- 当预值为0.5的情况,可以得到右上角这样的一个混淆矩阵,它正类是一个都没预测对,尽管是在这么差的情况下,左边的ROC曲线,看上去分类器效果仍然非常好,而右边这个分类器能够反映出这个模型效果不太好。
所以在这种情况下,我们需要选用 PR曲线,也就是说,如果我们更关心的是正类预测结果,并且给到的数据集非常的不平衡的话,那我们一定要选用PR曲线,而不能选用ROC曲线。
学习视频
机器学习 | 模型评估: ROC曲线与PR曲线(一): ROC曲线与PR曲线的关系
机器学习 | 模型评估: ROC曲线与PR曲线(二): ROC曲线与PR曲线的适用场景
参考博客
深度学习评估方法
常用的分类模型性能评价指标
相关文章:
机器学习|正则化|评估方法|分类模型性能评价指标|吴恩达学习笔记
前文回顾:逻辑回归 目录 📚正则化 🐇过拟合的问题 🐇代价函数 🐇正则化线性回归 🐇正则化的逻辑回归模型 📚模型评估方法 🐇留出法(hold-out) &#…...

python迭代器详解
不懂的问题:什么是协变、逆变?渐进式? _T_co TypeVar("_T_co", covariantTrue) # Any type covariant containers.作者:20岁爱吃必胜客(坤制作人),近十年开发经验, 跨域学习者&…...

关于Docker逃逸
关于Docker逃逸 文章目录关于Docker逃逸前言一、判断是否为docker容器?二、privileged特权模式启动容器逃逸三、 Docker Remote API未授权访问逃逸四、危险挂载导致Docker逃逸五、危险挂载Docker Socket逃逸六、 挂载宿主机procfs逃逸七、脏牛漏洞来进行docker逃逸八…...

@Autowired和@Resource区别
Autowired和Resource到底有什么区别 Autowired 和 Resource 都是用来实现依赖注入的注解(在 Spring/Spring Boot 项目中),但二者却有着 5 点不同: 来源不同:Autowired 来自 Spring 框架,而 Resource 来自…...
动态内存管理详细讲解
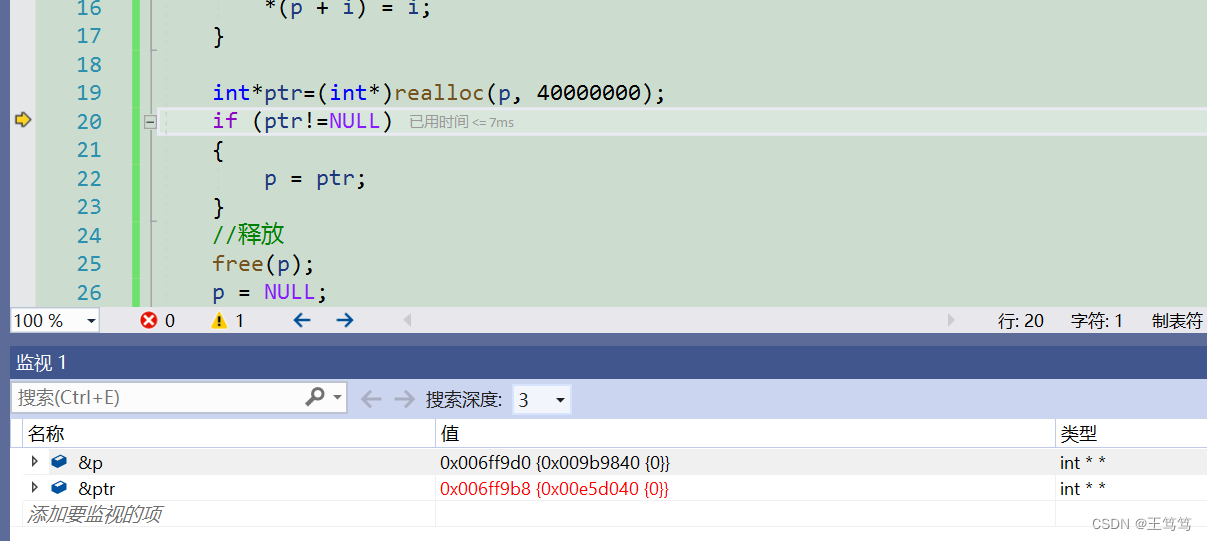
目录 1.为什么存在动态内存分配 2. 动态内存函数的介绍 2.1 malloc和free 2.2 calloc 2.3 realloc 今天要和大家分享的内容是的动态内存管理,我们先从他的定义入手学习。 1.为什么存在动态内存分配 我们到现在已经掌握了内存开辟的方式就是要么创建一个变量…...
Python和Excel的完美结合:常用操作汇总(案例详析)
在以前,商业分析对应的英文单词是Business Analysis,大家用的分析工具是Excel,后来数据量大了,Excel应付不过来了(Excel最大支持行数为1048576行),人们开始转向python和R这样的分析工具了&#…...

卡特兰数、斯特林数基础
卡特兰数 从格点(0,0)(0,0)(0,0)走到格点(n,n)(n,n)(n,n),只能向右或向上走,不能穿过对角线,的路径的条数,称为卡特兰数HnH_nHn。 则有H01H_01H01。 通项公式: Hn(2nn)−(2nn−1)H_n\begin{pmatrix} 2n\\ n \en…...
STL——mapmultimap和setmultiset
一、关联式容器 与序列式容器相同,关联式容器也是用于存储数据的,不同的是,关联式容器里存储的是<key, value>结构的键值对,在数据检索时比序列式容器效率更高。 二、键值对 用来表示具有一一对应的一种结构,该…...
2023热门抖音权重查询小程序源码
2023热门抖音权重查询小程序源码 跟抖音上很火的一模一样,小程序适配优化。接口免费。小程序不是网页 修改教程: 1,如果想修改或者去除水印,直接删除或修改“index.html”12~22行 2,如果想修改logo,直接…...

153.网络安全渗透测试—[Cobalt Strike系列]—[生成hta/exe/宏后门]
我认为,无论是学习安全还是从事安全的人多多少少都会有些许的情怀和使命感!!! 文章目录一、后门简介1、hta后门2、exe后门3、宏病毒后门二、生成后门并测试0、测试环境1、生成hta后门并测试2、生成exe后门并测试3、生成宏病毒后门…...

如何成为优秀的程序员
崔宝秋,现任小米首席架构师、小米云平台负责人。1995年赴美留学,纽约州立大学石溪分校计算机科学系博士毕业,曾任IBM高级工程师和高级研发经理、雅虎搜索技术核心团队主任工程师、LinkedIn主任工程师,2012年回国加入小米科技。 20…...
多线程(四):线程安全
在开始讲解线程安全之前我们先来回顾一下我们学了那些东西了: 1. 线程和进程的认识 2. Thread 类的基本用法 3. 简单认识线程状态 4. 初见线程安全 上一章结束时看了一眼线程安全问题,本章将针对这个重点讲解。 一个代码在单线程中能够安全执行&am…...
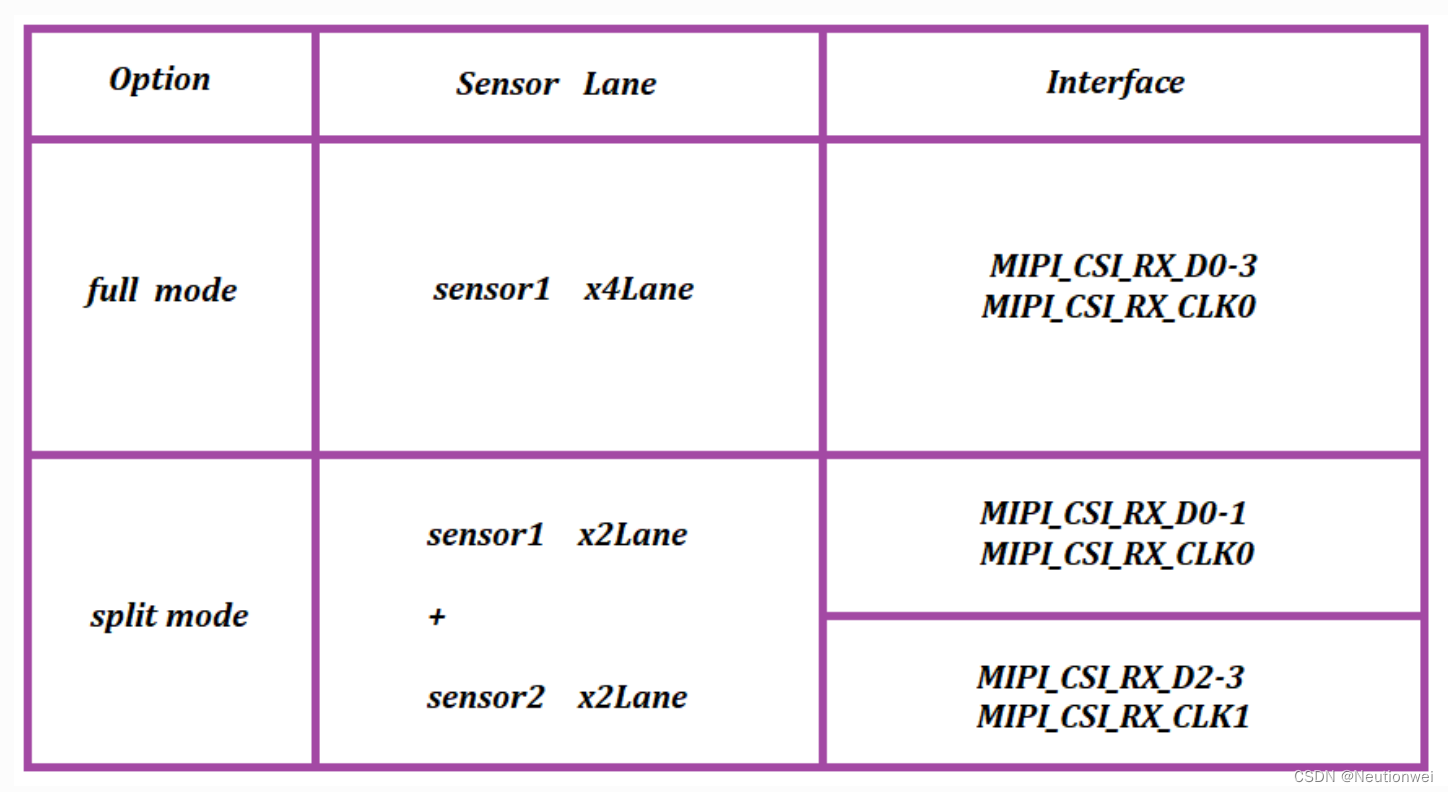
[ROC-RK3568-PC] [Firefly-Android] 10min带你了解Camera的使用
🍇 博主主页: 【Systemcall小酒屋】🍇 博主追寻:热衷于用简单的案例讲述复杂的技术,“假传万卷书,真传一案例”,这是林群院士说过的一句话,另外“成就是最好的老师”,技术…...

C++之模拟实现string
文章目录前言一、包含的相关头文件二、构造和析构1.构造函数2.拷贝构造1.传统写法2.现代写法3.赋值运算符重载1.传统写法2.现代写法4.析构函数三、iterator四、modify1.push_back(尾插一个字符)2.append(尾插一个字符串)3.运算符重载1.尾插字…...
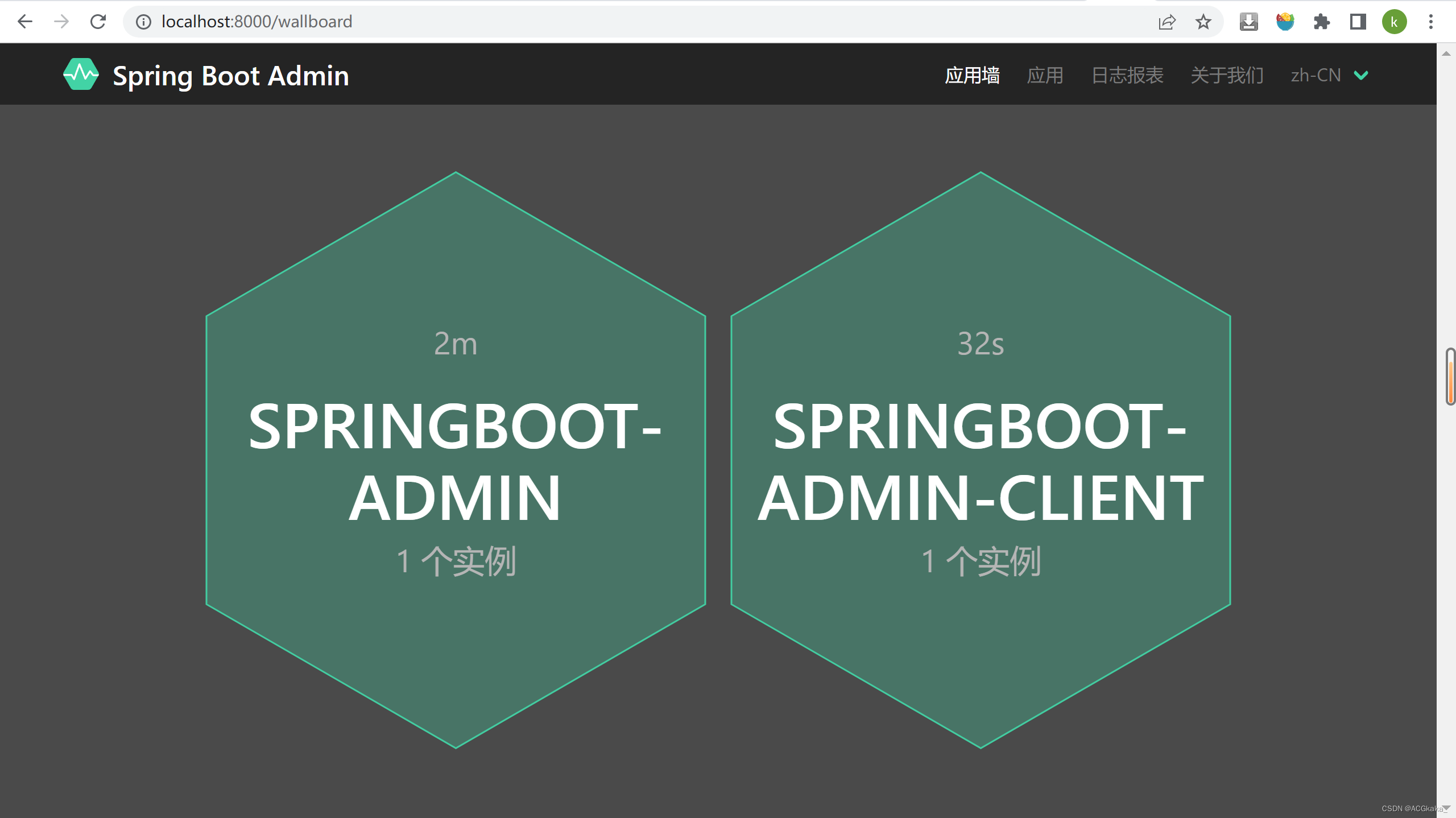
SpringBoot实战(十三)集成 Admin
目录一、简介二、搭建 springboot-admin 管理服务1.Maven 依赖2.application.yml3.添加 EnableAdminServer4.启动服务,查看页面三、搭建 springboot-admin-client 客户端服务1.Maven 依赖2.application.yml3.启动服务,查看页面四、搭配 Eureka 使用1.搭建…...

mke2fs命令:建立ext2文件系统
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 使用格式 mke2fs [options] [设备名称] [区块数] options与含义 -c:检查是否有损坏的区块。-F:不管指定的设备为何,强制执行mke2fs。-M:记录最后一次挂入的…...

免费分享一个springboot+vue的办公系统
springbootvue的OA系统项目介绍项目部署项目特点项目展示项目介绍 这是一个采用前后端分离开发的项目,前端采用 Vue 开发、后端采用 SpringBoot Mybatis 开发。 很适合java初学者练手和学习。 前端技术:Vue3.2 Vue-Router Pinia Ant Design Vue 3.X…...
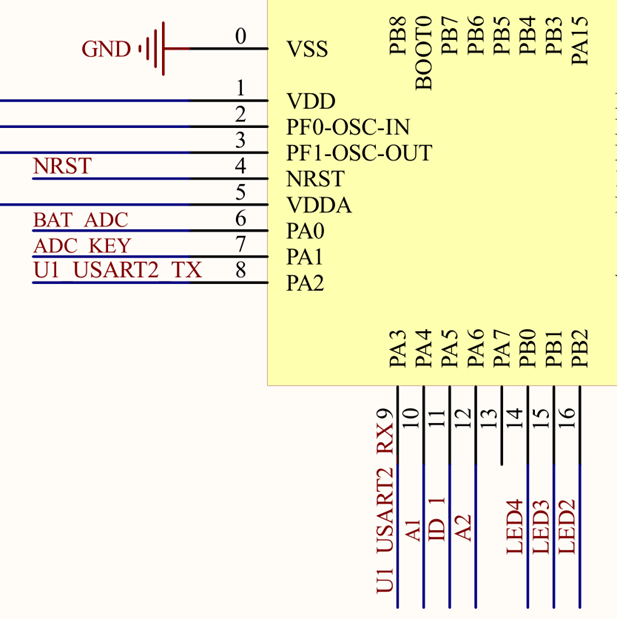
STM32数据搬运工DMA
DMA的概念DMA,全称为:Direct Memory Access,即直接存储器访问。DMA 传输方式无需 CPU 直接控制传输,也没有中断处理方式那样保留现场和恢复现场的过程,通过硬件为 RAM 与 I/O 设备开辟一条直接传送数据的通路ÿ…...

4、操作系统——进程间通信(2)(system V-IPC介绍)
目录 一、system V-IPC常识 1、key和ID 2、文件描述符 3、函数(ftok) ftok产生IPC对象的健值key(类似文件路径) 4、例子 5、使用命令查看或删除当前系统中的IPC对象 一、system V-IPC常识 1、key和ID (1&#x…...

基于CentOS Stream 9平台搭建Nacos2.0.4集群以及OpenResty反向代理
目录展示Nacos2.0.4集群搭建1. 下载2. 解压3.修改配置3.1分别修改下启动类中JDK路径以及启动大小3.2 分别配置数据源3.3 创建nacos数据库3.4 修改cluster.conf配置3.4.1 复制并修改3.4.2 编辑文件,修改三台主机地址3.4.3 分别放入另外两个nacos的conf目录下:4. 启动…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...