【蓝桥杯集训·周赛】AcWing 第96场周赛
文章目录
- 第一题 AcWing 4876. 完美数
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第二题 AcWing 4877. 最大价值
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第三题 AcWing 4878. 维护数组
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
第一题 AcWing 4876. 完美数
一、题目
1、原题链接
4876. 完美数
2、题目描述
如果一个正整数能够被 2520 整除,则称该数为完美数。
给定一个正整数 n,请你计算 [1,n] 范围内有多少个完美数。
输入格式
一个整数 n。
输出格式
一个整数,表示 [1,n] 范围内完美数的个数。
数据范围
前 3 个测试点满足 1≤n≤3000。
所有测试点满足 1≤n≤1018。输入样例:
3000输出样例:
1
二、解题报告
1、思路分析
(1)注意数据范围要开long long。
(2)因为能够被2520整除的是2520的倍数,所以当前n是2520的多少倍(下取整),即存在多少个能够被2520整除的数。
2、时间复杂度
时间复杂度为O(1)
3、代码详解
#include <iostream>
using namespace std;
typedef long long LL;
LL n;
int main()
{ cin>>n; cout<<n/2520;return 0;
}
第二题 AcWing 4877. 最大价值
一、题目
1、原题链接
4877. 最大价值
2、题目描述
有一个容量为 n 的背包和 m+1 种物品,每种物品都有无限多个。
物品种类编号为 0∼m。
第 i 种物品的体积为 vi,价值为 wi。
在使用背包装入物品时,每种物品的限重如下:
- 第 0 种物品:重量忽略不计,在装入时没有重量限制。
- 第 1∼m 种物品:第 i 种物品的单个重量为 hi,如果该种物品的装入总重量超过 li,则视为超重。
现在,请你挑选物品装入背包,要求
- 所有装入物品的总体积不得超过背包容量。
- 所有存在重量限制的物品均不得超重。
- 满足以上所有条件的前提下,所有装入物品的总价值尽可能大。
输出总价值的最大可能值。
注意审题,不要将 n,m 的含义弄混。
输入格式
第一行包含四个整数 n,m,v0,w0。
接下来 m 行,每行包含四个整数 li,hi,vi,wi。
输出格式
一个整数,表示总价值的最大可能值。
数据范围
前 4 个测试点满足 1≤n≤100,1≤m≤2。
所有测试点满足 1≤n≤1000,1≤m≤10,1≤li,hi,vi,wi≤100。输入样例1:
10 2 2 1 7 3 2 100 12 3 1 10输出样例1:
241输入样例2:
100 1 25 50 15 5 20 10输出样例2:
200
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)装入第0个物品相当于是0-1背包问题,而装入后面物品相当于是多重背包问题(也可以直接看成多重背包问题,将第一个物品的数量设置为正无穷)。
(2)按照上述思路进行求解即可。
2、时间复杂度
时间复杂度为O(n2)
3、代码详解
法1
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int dp[N],w[N],v[N],l[N],h[N];
int n,m;
int main(){cin>>n>>m>>v[0]>>w[0];for(int i=1;i<=m;i++) cin>>l[i]>>h[i]>>v[i]>>w[i];//完全背包,处理第0件物品for(int j=v[0];j<=n;j++) dp[j]=max(dp[j],dp[j-v[0]]+w[0]);//多重背包,处理后面物品for(int i=1;i<=m;i++){for(int j=n;j>=v[i];j--){for(int k=0;k*v[i]<=j&&k<=l[i]/h[i];k++){dp[j]=max(dp[j],dp[j-k*v[i]]+k*w[i]);}}}cout<<dp[n];return 0;
}
法2
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int v[N],w[N],l[N],h[N];
int dp[N];
int n,m;
int main()
{ cin>>n>>m>>v[0]>>w[0];l[0]=0x3f3f3f3f,h[0]=1; //初始化第0件物品可以装无限个,即l[0]/h[0]=正无穷for(int i=1;i<=m;i++){cin>>l[i]>>h[i]>>v[i]>>w[i];}//转化成多重背包问题求解for(int i=0;i<=m;i++){for(int j=n;j>=0;j--){for(int k=0;k<=l[i]/h[i]&&k*v[i]<=j;k++)dp[j]=max(dp[j],dp[j-k*v[i]]+k*w[i]); }}cout<<dp[n];return 0;
}
第三题 AcWing 4878. 维护数组
一、题目
1、原题链接
4878. 维护数组
2、题目描述
给定一个长度为 n 的整数序列 d1,d2,…,dn 以及三个整数 k,a,b。
初始时,所有 di 均为 0。
你需要对序列依次进行 q 次操作,操作分为以下两种:
1 x y,将 dx 增加 y。2 p,计算并输出输入格式
第一行包含 5 个整数 n,k,a,b,q。
接下来 q 行,每行描述一个操作,格式如题面所述。
输出格式
每个
2 p操作,输出一行一个整数表示结果。数据范围
前 3 个测试点满足 1≤k≤n≤10,1≤q≤10。
所有测试点满足 1≤k≤n≤2×105,1≤b<a≤10000 ,1≤q≤2×105,1≤x≤n,1≤y≤10000,1≤p≤n−k+1。输入样例1:
5 2 2 1 8 1 1 2 1 5 3 1 2 1 2 2 1 4 2 1 3 2 2 1 2 3输出样例1:
3 6 4输入样例2:
5 4 10 1 6 1 1 5 1 5 5 1 3 2 1 5 2 2 1 2 2输出样例2:
7 1
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)利用两个树状数组分别维护min(d[i],b)、min(d[i],a)。
(2)
tr1[]维护min(d[i],b):即针对每次add()操作,始终保持tr1[]维护的数组(设为B[],每个d[i]对应B[i],即B[]对应的树状数组为tr1[],而且B[]中的数均小于等于b),即如果当d[x]小于b的时候需要判断d[x]+y以之后的值与b的大小关系:如果d[x]+y<=b,则保留该增值(即让对应d[x]的B[x]中的数的值B[x]+y);如果d[x]+y>b,由于我们不能使维护的数组B[]中的数大于b,所以我们最多只能让其增加到b(即让B[x]增加它距离b的差值b-d[x],也就是让他对应的维护的数组的值B[x]只增加到b)。如果此时d[x]>=b,我们不再需要对维护的数组B[X]进行增值操作,因为其对应的B[x]中的值已经达到b,无论对d[x]增加多少都不会影响B[x]。tr2[]维护min(d[i],a),同理。
(3)问题所求即为:tr1[]在[1,p-1]的区间和+tr2[]在[p+k,n]的区间和。
2、时间复杂度
时间复杂度为O(nlogn)
3、代码详解
#include <iostream>
#include <algorithm>
using namespace std;
const int N=200010;
typedef long long LL;
int d[N],tr1[N],tr2[N];
int n,k,a,b,q;
//lowbit运算
int lowbit(int x){return x&-x;
}
//点更新,在tr[x]位置加c
void add(int tr[],int x,int c){for(int i=x;i<=n;i+=lowbit(i)){tr[i]+=c;}
}
//求[1,x]前缀和
int query(int tr[],int x){LL ans=0;for(int i=x;i;i-=lowbit(i)){ans+=tr[i];}return ans;
}
//求[i,j]区间和
int sum(int tr[],int i,int j){return query(tr,j)-query(tr,i-1);
}
int main()
{ cin>>n>>k>>a>>b>>q;while(q--){int op;cin>>op;if(op==1){int x,y;cin>>x>>y;if(d[x]<=b) add(tr1,x,d[x]+y>=b?b-d[x]:y); //维护min(d[i],b)if(d[x]<=a) add(tr2,x,d[x]+y>=a?a-d[x]:y); //维护min(d[i],a)d[x]+=y;}else{int p;cin>>p;LL ans=sum(tr1,1,p-1)+sum(tr2,p+k,n); //求题目两个区间和cout<<ans<<endl;} }return 0;
}
相关文章:
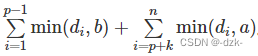
【蓝桥杯集训·周赛】AcWing 第96场周赛
文章目录第一题 AcWing 4876. 完美数一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4877. 最大价值一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4878. 维护数组一、题目1、原…...
【数据结构】顺序表的深度刨剖析
前言:在上一篇文章中,我们已经对数据结构有了一定了解,我们可以通过优化空间复杂度或者时间复杂度从而提高我们程序运行或存储速率。至此我们就知道了数据结构的重要性,所以今天我们将要了解和学习一种实用的数据结构——线性表。…...

Unity 之 使用原生UGUI实现随手移动摇杆功能经典实例
Unity 之 使用原生UGUI实现随手移动摇杆功能实现效果一,实现思路1.1 原理解析1.2 思路概述二,实现代码2.1 随手落下2.2 摇杆转动三,源码分享3.1 场景搭建3.2 完整代码3.3 实现效果实现效果 本文最终实现效果: 一,实现…...
Linux内核源代码概述
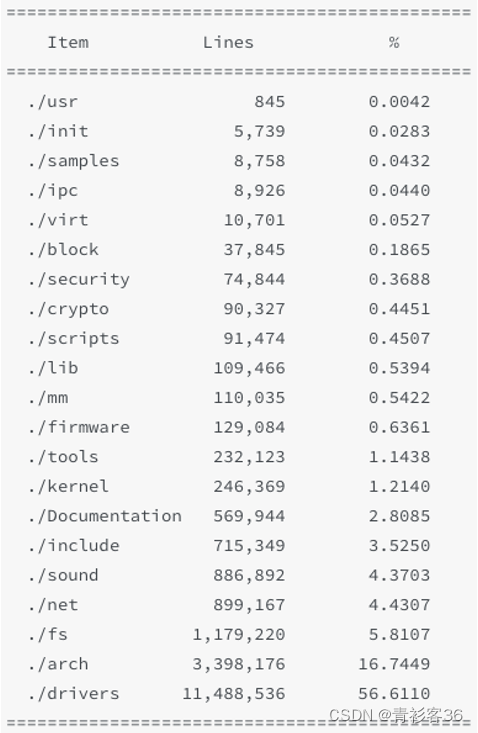
Linux内核源代码非常庞大,截止到2015年据统计代码总量就已经超过1500万行(LOC,Line of Code),看代码总量非常吓人,具体看这1500万行代码的大致分布情况如下图。 显然占比最大的drivers和arch目录下的代码合…...
Nginx 教程-动静分离
一、Nginx 动静分离理论1、概念今天学习和梳理Nginx动静分离,动静分离是将网站静态资源(HTML,JavaScript,CSS,img等文件)与后台应用分开部署,之所以要进行动静分离,其一为了提高前端…...

自己设计的网站,如何实现分页功能?(详细代码+注释)
目录 前言 实现分页功能 需求分析 客户端开发 服务器开发 前后端交互——两种前端得到 文章总页数 的方法,那种更合适? 前言 你在设计网站的时候是否有过这样的烦恼:“我设计的网站怎么就是从上到下一条线内容全部展开,一点都…...
STM32F407控制微型推拉式电磁铁(通过继电器)
1、继电器 继电器相当于开关,单片机通过io口高低电平的控制来控制继电器的开闭。采用继电器的好处除了能够用低电压控制高电压(如32单片机控制220V的电压)外,还可以防止电流反冲,弄烧单片机。 本文采用3.3v的电磁铁&am…...
VS Code工作区用法
背景VS Code可以通过"文件/打开文件夹"来打开本地项目,但是想要打开多个项目便需要来回切换,比较费劲。此时就可以使用工作区功能,将不同的项目放置到同一个工作区中,这样切换项目的时候就会非常方便。操作方法打开其中…...

Mybatis-Plus SQLFeatureNotSupportedException: getObject with type问题解决
问题描述: Error attempting to get column modify_time from result set. Cause: java.sql.SQLFeatureNotSupportedException: getObject with type ; getObject with type; nested exception is java.sql.SQLFeatureNotSupportedException: getObject with type…...

Unity | 发布Android的那些事儿
1.使用UnityWebRequest获取StreamingAssets中的json文件(1)直接根据不同平台指定url路径IEnumerator AITalPredZhanHui(){string url;string fileName "girl.json"; #if UNITY_EDITOR || UNITY_STANDALONEurl "file://" Applicat…...

git为什么要先commit,然后pull,最后再push?而不是commit完直接push?
情况是这样的,现在远程有一个仓库,分支就一个,是master。然后我本地的仓库是从远程的master上clone下来的。大家都是clone下来,再在自己本地改好,再commit然后pull然后push,大家都是这么做的。那么现在问题…...
)
若依框架----源码分析(@RateLimiter)
若依作为最近非常火的脚手架,分析它的源码,不仅可以更好的使用它,在出错时及时定位,也可以在需要个性化功能时轻车熟路的修改它以满足我们自己的需求,同时也可以学习人家解决问题的思路,提升自己的技术水平…...
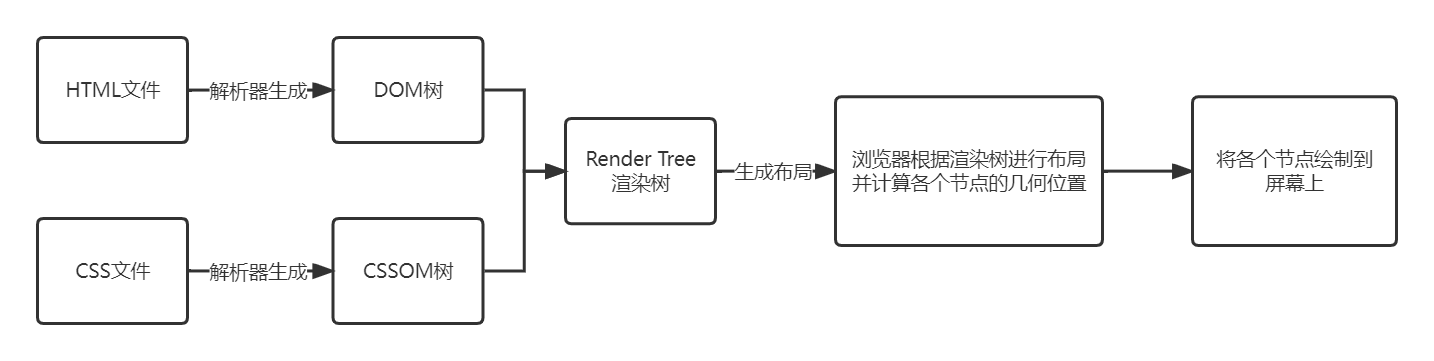
页面的重排和重绘?
思路: 网页渲染HTML文件到浏览器的过程->定义->如何优化网页渲染HTML文件到浏览器的过程HTML 文件通过HTML解析器解析生成DOM树;CSS文件通过CSS解析器生成CSSOM树;DOM树和CSSOM树生成渲染树(render tree)&#x…...

人脸检测-python和c++实现
人脸检测是计算机视觉领域中的一个重要应用,其目的是从图像或视频中自动检测出其中的人脸,并对其进行识别、跟踪等操作。人脸检测技术已经广泛应用于安防、人机交互、娱乐等领域,具有广泛的应用前景。 人脸检测的基本思路可以分为以下几个步骤: 图像预处理:首先需要对输入…...
PowerJob源码环境搭建
一、IEDA导入PowerJob源码 gitgithub.com:PowerJob/PowerJob.gitPowerJob 由调度服务器(powerjob-server)和执行器(powerjob-worker)两部分组成 powerjob-server 负责提供 Web 服务和完成任务的调度powerjob-worker 则负责执行用…...

天梯赛刷题小记 —— L2
最近在重刷 天梯赛,浅浅记录一下,进入L2阶段了 L2-001 紧急救援 解题思路:典型的dijkstra模板题,带路径记录与权重,方案数记录,解析出过 Dijkstra(兼路径) #include <bits/stdc.h> #define inf…...

Prometheus监控实战系列十九:监控Kubernetes集群(上)
Kuberentes是一款开源的容器编排产品,由Google开发后发布到社区,并在2015年将该项目捐献给了云原生基金会(Cloud Native Computing Foundation)。从2014年第一个版本发布以来,Kubernetes便迅速获得开源社区的追捧&…...

番茄学习法——亲测超级好用
今天给大家分享下我最近使用的学习方法,真的非常好用!大家用起来! 在日常的学习和工作中,我们经常会遇到一些难以克服的问题:分心、效率低下、焦虑等。为了帮助人们更好地学习和工作,一些学习方法和工具应运…...
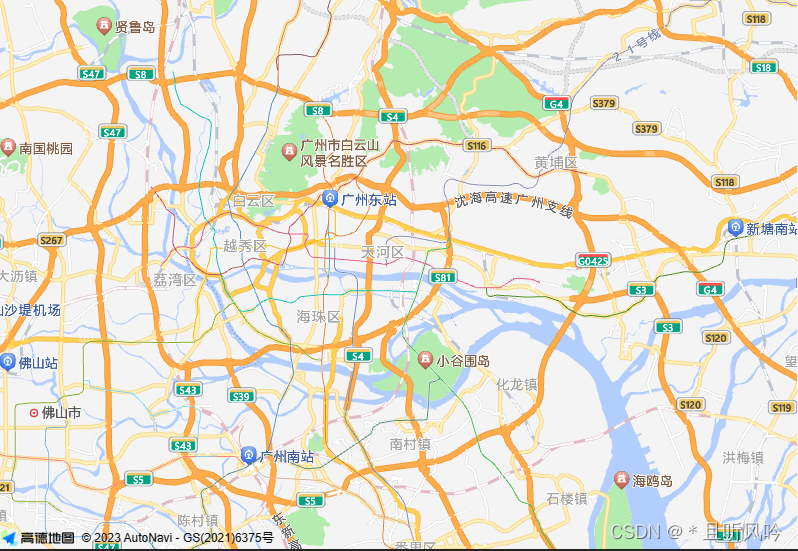
vue 项目中使用高德地图
一、账号准备 首先,需要注册并登录高德地图开放平台,申请密钥。操作指引:高德地图开放平台 二、安装高德地图加载器 npm 安装: npm i amap/amap-jsapi-loader --save或者 yarn 安装: yarn add amap/amap-jsapi-loa…...

【每日一题】病人排队
题目描述小理是个热爱生活的孩子。病人登记看病,小理想编写一个程序,将登记的病人按照以下原则排出看病的先后顺序:1. 老年人(年龄 ≥≥ 60岁)比非老年人优先看病。2. 老年人按年龄从大到小的顺序看病,年龄…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
