动态规划---线性dp和区间dp
动态规划(三)
目录
- 动态规划(三)
- 一:线性DP
- 1.数字三角形
- 1.1数字三角形题目
- 1.2代码思路
- 1.3代码实现(正序and倒序)
- 2.最长上升子序列
- 2.1最长上升子序列题目
- 2.2代码思路
- 2.3代码实现
- 3.最长公共子序列
- 3.1最长公共子序列题目
- 3.2代码思路
- 3.3代码实现
- 4.石子合并
- 4.1题目如下
- 4.2代码思路
- 4.3代码实现
- 总结
一:线性DP
1.数字三角形
1.1数字三角形题目
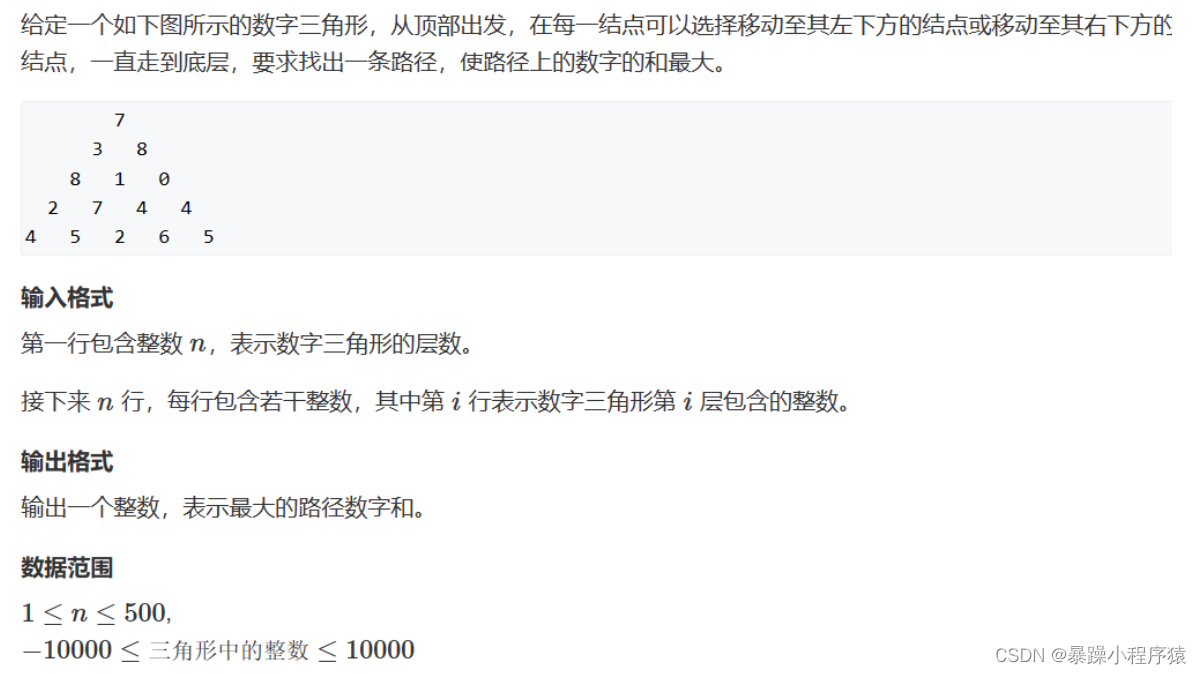
1.2代码思路
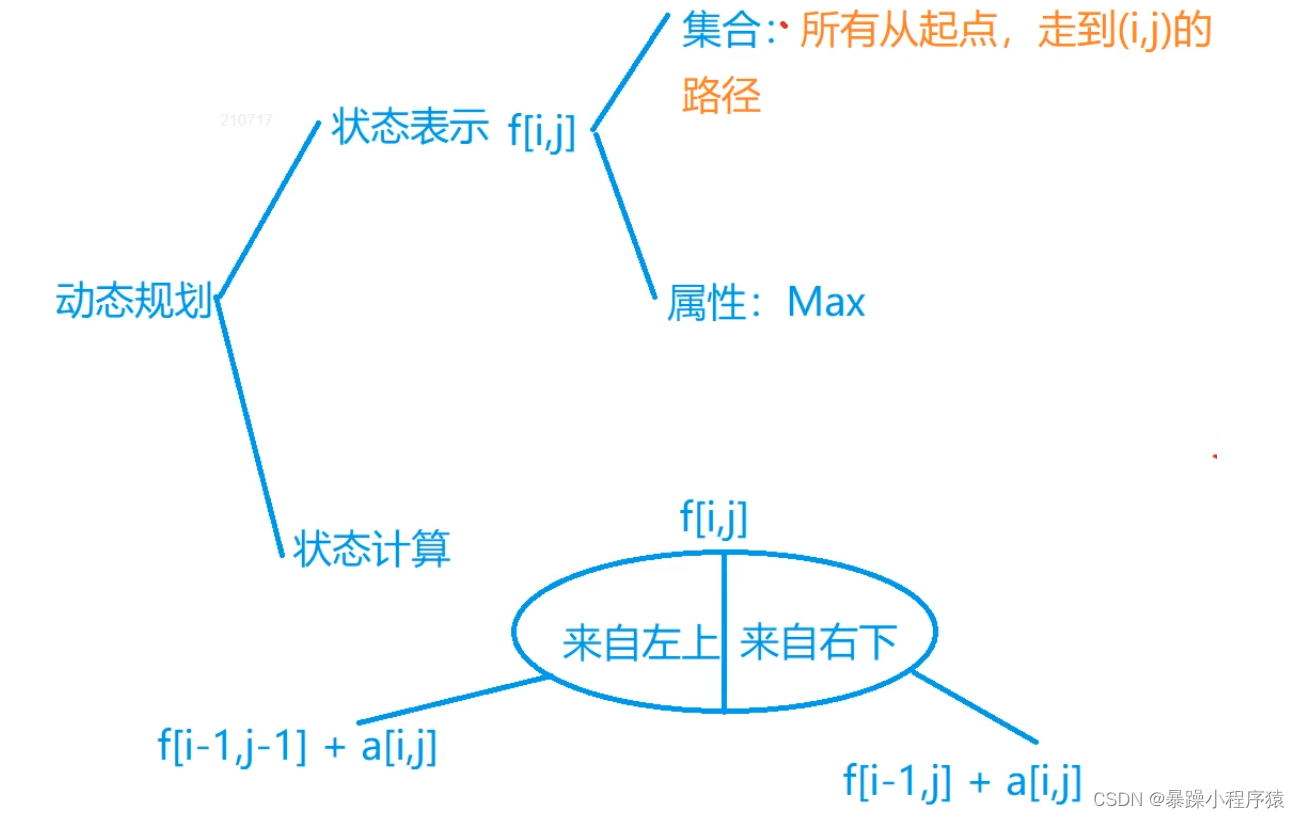
正序思路
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GCHTJR8G-1679754745663)(D:\acwing算法题目思路\acwing图片\image-20230313163539518.png)]](https://img-blog.csdnimg.cn/728b2fe370624df09e03090c5ab66257.png)
倒序思路

1.3代码实现(正序and倒序)
正序版本
#include<bits/stdc++.h>
using namespace std;const int N=510,INF=0x3f3f3f3f;
int f[N][N];
int a[N][N];int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){ for(int j=0;j<=i+1;j++){ //因为有负数,所以应该将两边也设为-INFf[i][j]=-INF;}}f[1][1]=a[1][1];for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);}}int res=-INF;for(int i=1;i<=n;i++) res=max(res,f[n][i]);cout<<res<<endl;
}
倒叙版本(倒序比正序好的地方就在不用考虑边界问题)
#include<bits/stdc++.h>
using namespace std;const int N=510;
int f[N][N];
int n;int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>f[i][j];}}for(int i=n;i>=1;i--){for(int j=i;j>=1;j--){f[i][j]=max(f[i+1][j],f[i+1][j+1])+f[i][j];}}cout<<f[1][1]<<endl;
}
2.最长上升子序列
2.1最长上升子序列题目
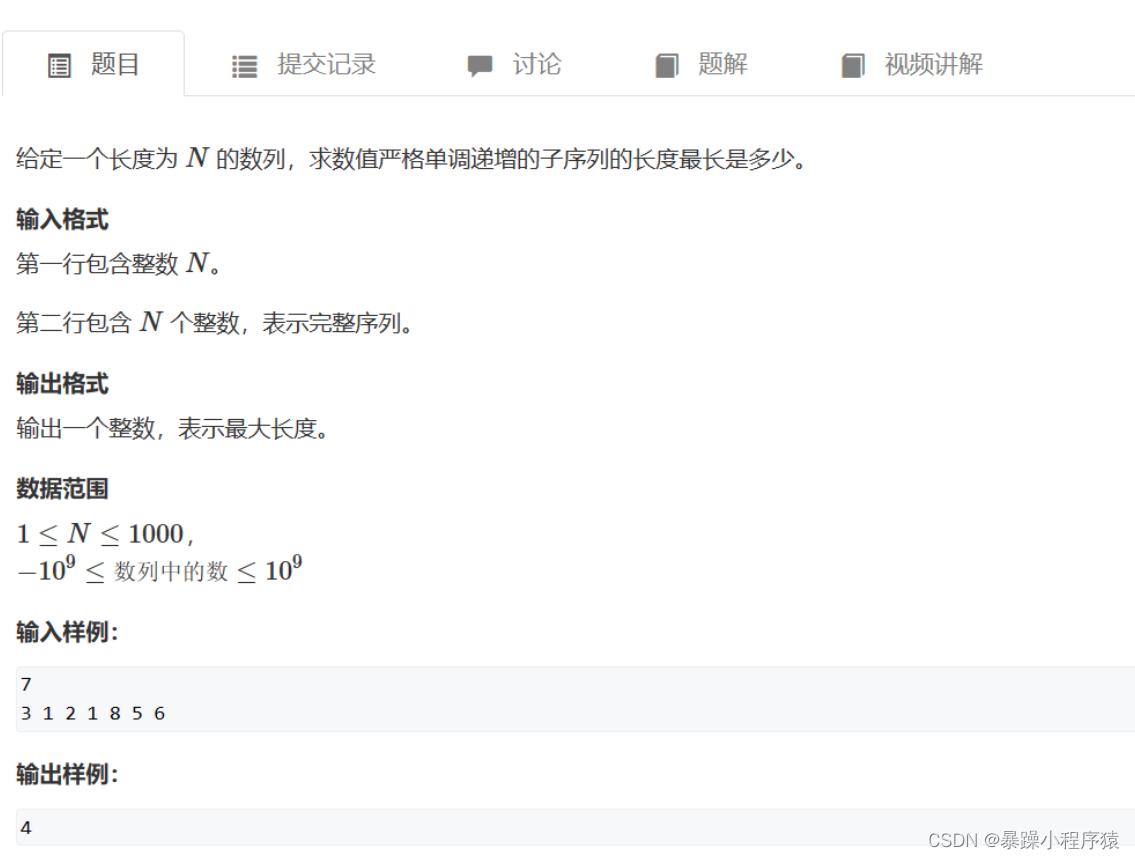
2.2代码思路
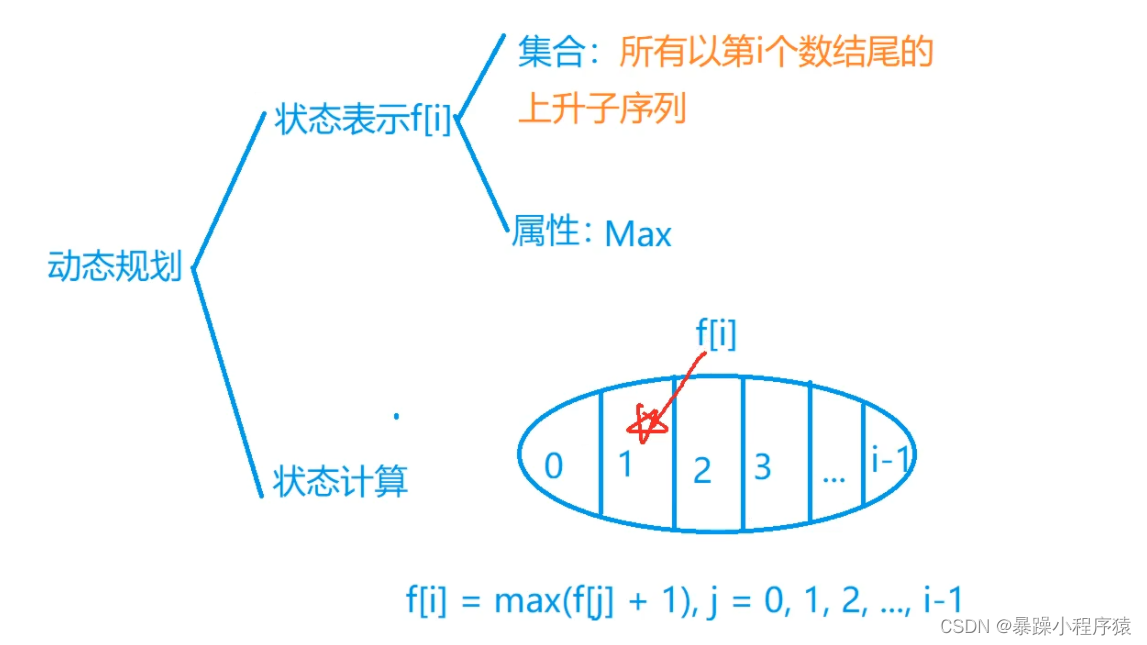

2.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n;
int a[N],f[N];//a[N]我们用来保存长度为n的序列//f[N]表示以指定数字结尾的单调递增的序列的最大长度
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=n;i++){f[i]=1;//只有a[i]一个数符合单调递增for(int j=1;j<i;j++){if(a[j]<a[i]){f[i]=max(f[i],f[j]+1);}}}int res=0;for(int i=1;i<=n;i++){res=max(res,f[i]);}printf("%d\n",res);return 0;
}
3.最长公共子序列
3.1最长公共子序列题目
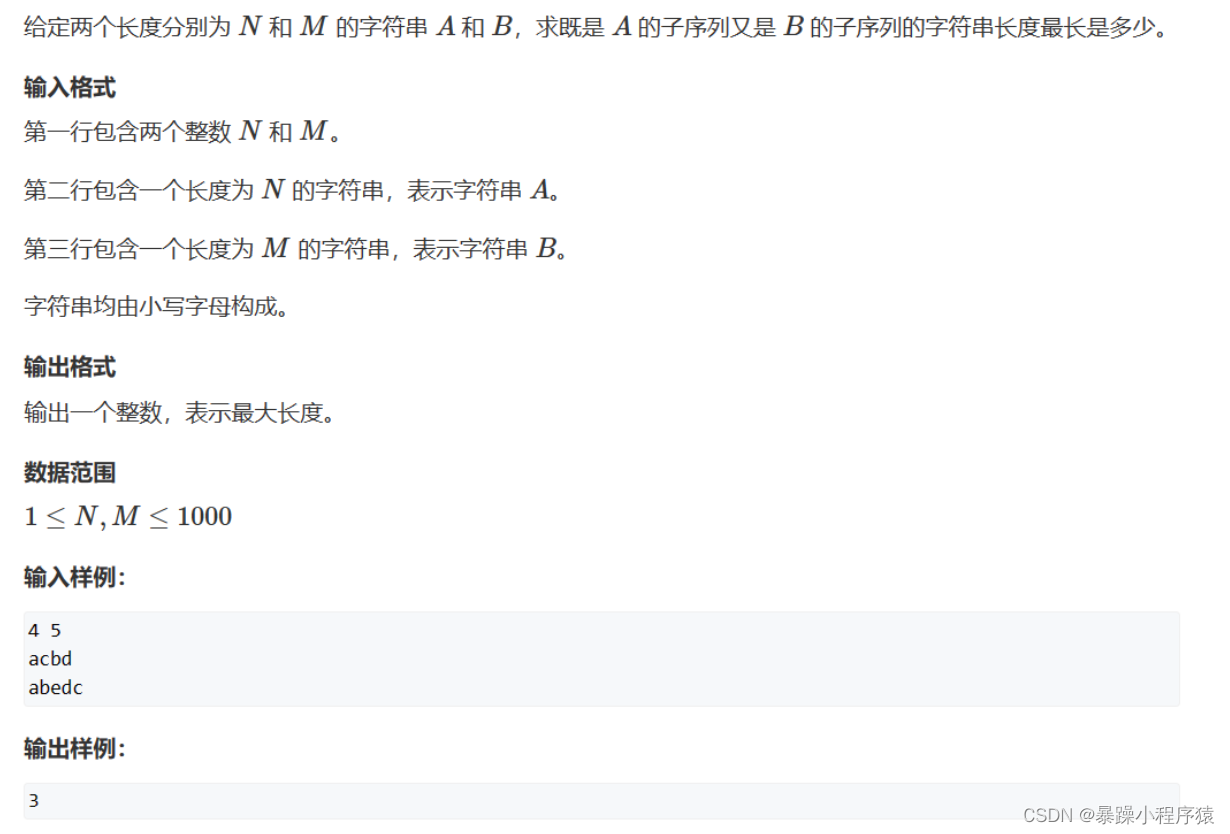
3.2代码思路
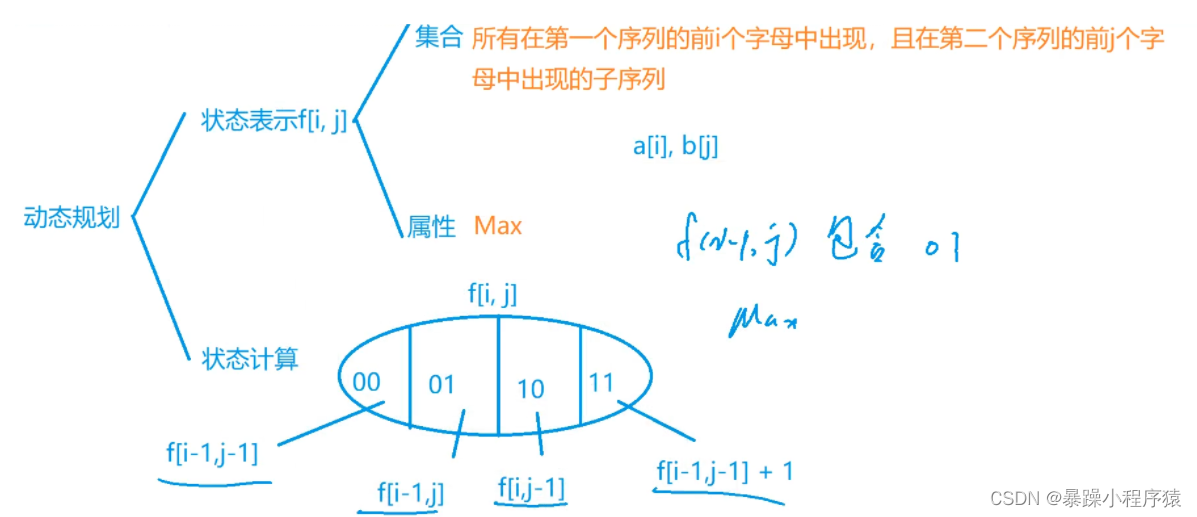
我觉得这题的状态分成两半考虑比较方便,按两个序列末尾的字符是不是相等来区分。
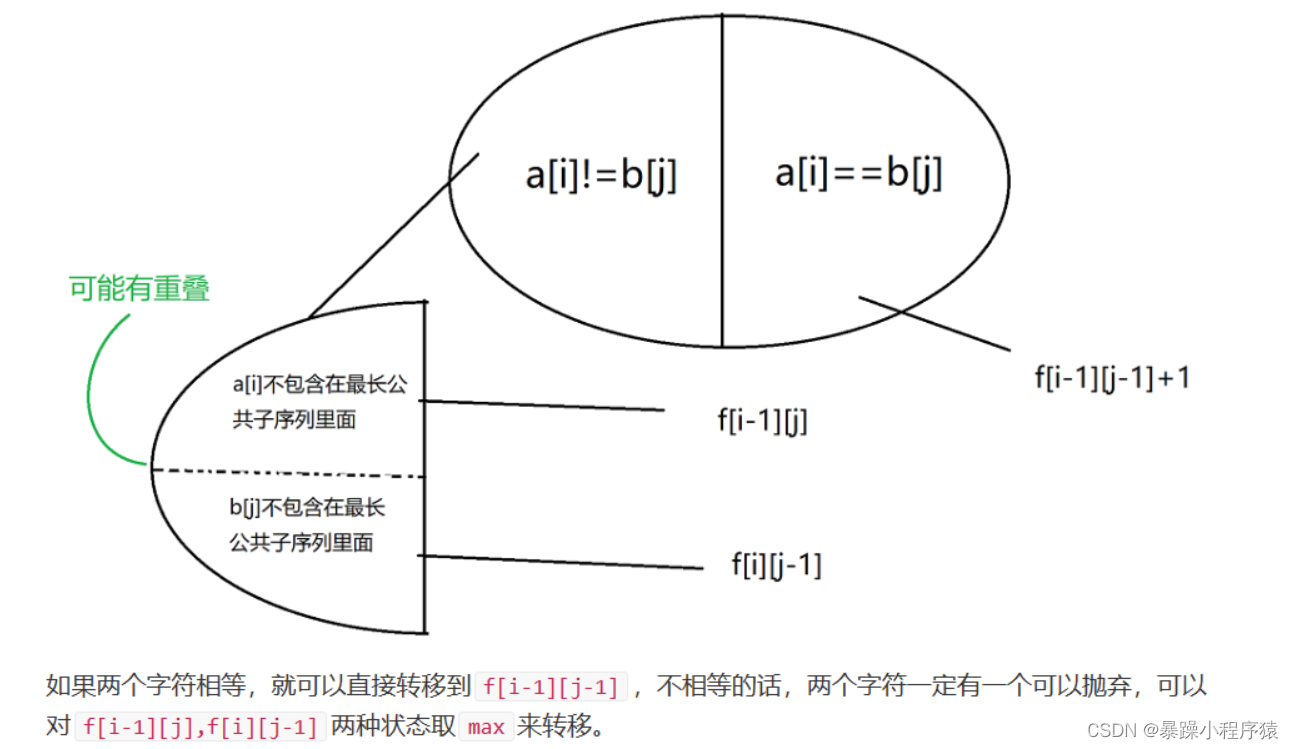
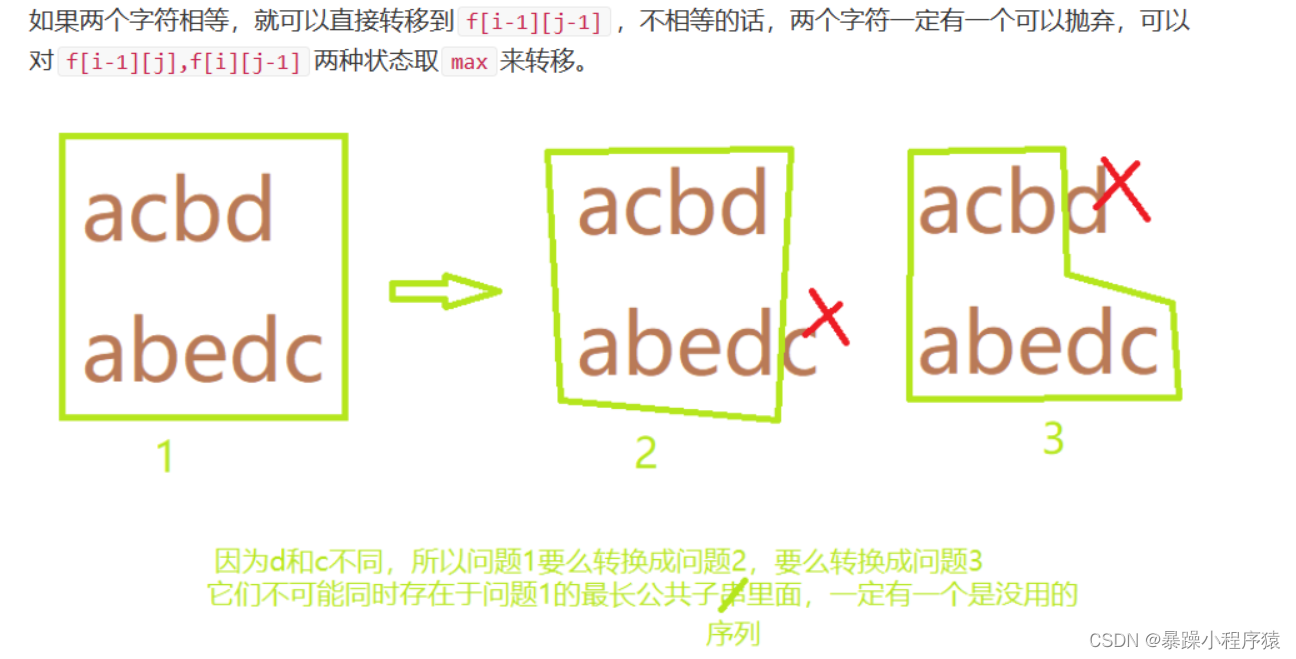
3.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;int n,m;char a[N],b[N];int f[N][N];int main(){scanf("%d%d",&n,&m);scanf("%s%s",a+1,b+1);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1]);if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);}}printf("%d\n",f[n][m]);return 0;}
4.石子合并
4.1题目如下
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lQ6plVYl-1679754745666)(D:\acwing算法题目思路\acwing图片\image-20230313171007224.png)]](https://img-blog.csdnimg.cn/bcbcb23e94834cb9ae8569a1ebcae324.png)
题目分析
假设有4堆石子:1 3 5 2
i=1,k=2,j=4
f[1,2]:将第一堆和第二堆这两堆石子合并成一堆石子
f[3,4]:将第三堆和第四堆这两堆石子合并成一堆石子
所以经过f[1,2]+f[3,4]后我们就成功将1 3 5 2这四堆石子合并成了4 7 这两堆石子
不过别忘了题目要求的是将这四堆石子合并成一堆石子
所以我们还需将4 7 这两堆石子合并成一堆石子
因此还需付出4+7=11的代价;而11=[1,4]的前缀和
总代价:(1+3)+(5+2)+4+7=22
假设有4堆石子:1 3 5 2
i=1,k=2,j=4
f[1,2]:将第一堆和第二堆这两堆石子合并成一堆石子
f[3,4]:将第三堆和第四堆这两堆石子合并成一堆石子
所以经过f[1,2]+f[3,4]后我们就成功将1 3 5 2这四堆石子合并成了4 7 这两堆石子
不过别忘了题目要求的是将这四堆石子合并成一堆石子
所以我们还需将4 7 这两堆石子合并成一堆石子
因此还需付出4+7=11的代价;而11=[1,4]的前缀和
总代价:(1+3)+(5+2)+4+7=22
4.2代码思路
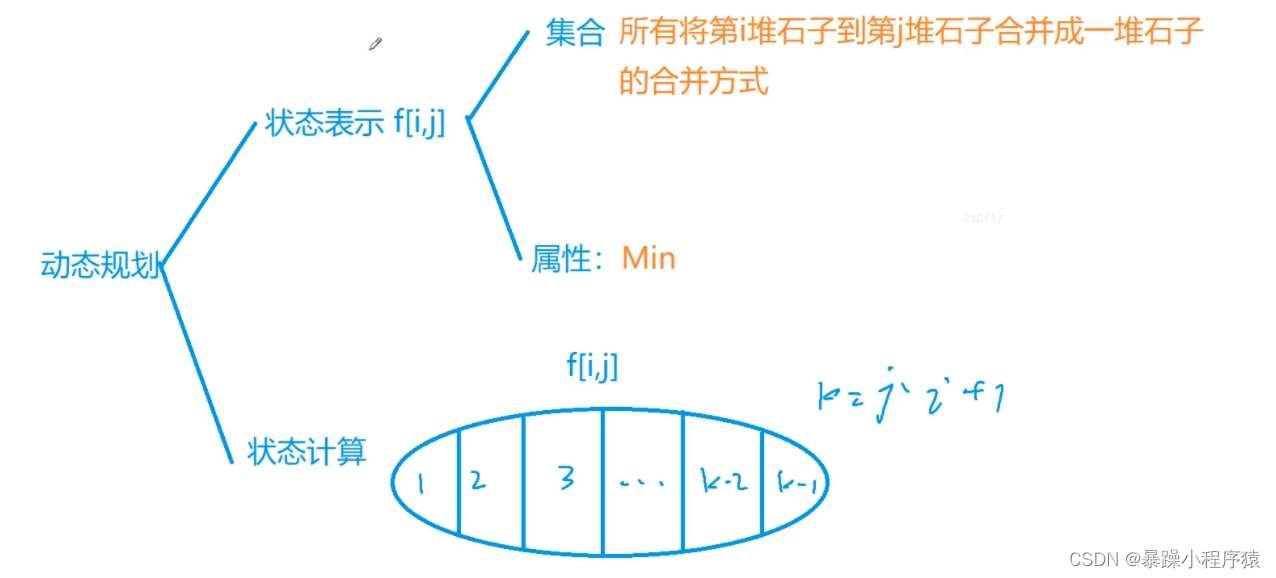
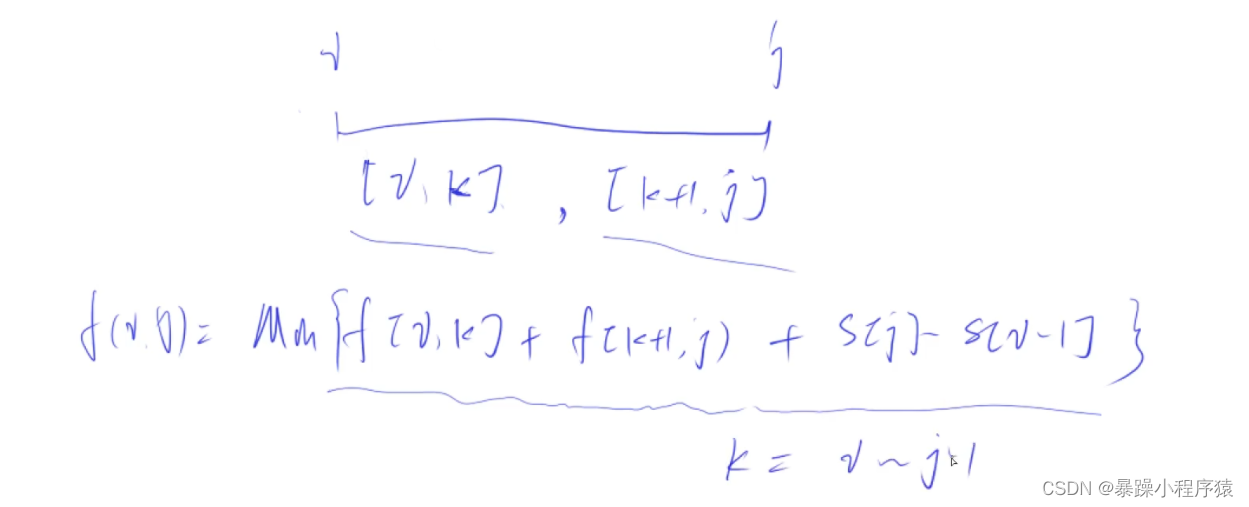
4.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;
const int N=310;
int n;
int s[N];
int f[N][N];int main()
{scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&s[i]);for(int i=1;i<=n;i++) s[i]+=s[i-1];for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int l=i,r=i+len-1;f[i][r]=1e8;for(int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}}}printf("%d\n",f[1][n]);return 0;
}
总结
本篇博客涉及了线性dp和区间dp,还有对应的算法题目讲解帮助理解算法,希望对大家有帮助~
相关文章:
动态规划---线性dp和区间dp
动态规划(三) 目录动态规划(三)一:线性DP1.数字三角形1.1数字三角形题目1.2代码思路1.3代码实现(正序and倒序)2.最长上升子序列2.1最长上升子序列题目2.2代码思路2.3代码实现3.最长公共子序列3.1最长公共子序列题目3.2代码思路3.3代码实现4.石子合并4.1题目如下4.2代…...

常见的2D与3D碰撞检测算法
分离轴分离轴定理(Separating Axis Theorem)是用于解决2D或3D物体碰撞检测问题的一种方法。其基本思想是,如果两个物体未发生碰撞,那么可以找到一条分离轴(即一条直线或平面),两个物体在该轴上的…...

STM32 10个工程篇:1.IAP远程升级(二)
一直提醒自己要更新CSDN博客,但是确实这段时间到了一个项目的关键节点,杂七杂八的事情突然就一涌而至。STM32、FPGA下位机代码和对应Labview的IAP升级助手、波形设置助手上位机代码笔者已经调试通过,因为不想去水博客、凑数量,复制…...
Unity+ChatGpt的联动 AICommand
果然爱是会消失的,对吗 chatGpt没出现之前起码还看人家的文章,现在都是随便你。 本着师夷长技以制夷的思路,既然打不过,那么我就加入 github地址:https://github.com/keijiro/AICommand 文档用chatGpt翻译如下&#…...
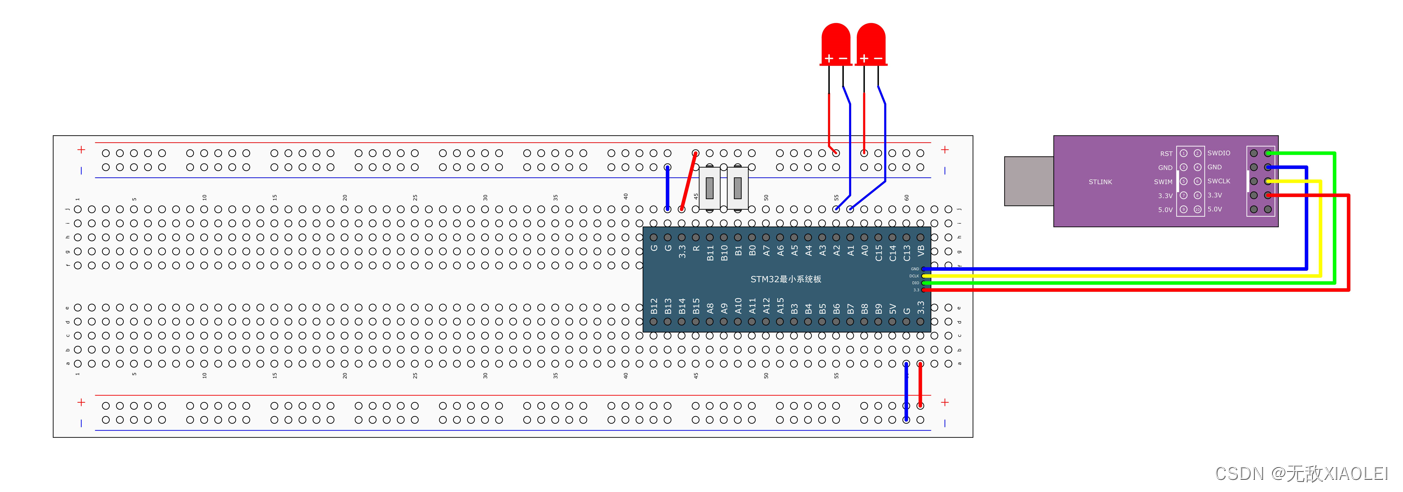
STM-32:按键控制LED灯 程序详解
目录一、基本原理二、接线图三、程序思路3.1库函数3.2程序代码注:一、基本原理 左边是STM322里电路每一个端口均可以配置的电路部分,右边部分是外接设备 电路图。 配置为 上拉输入模式的意思就是,VDD开关闭合,VSS开关断开。 浮空…...
北邮22信通:(8)实验1 题目五:大整数加减法(搬运官方代码)
北邮22信通一枚~ 跟随课程进度每周更新数据结构与算法的代码和文章 持续关注作者 解锁更多邮苑信通专属代码~ 上一篇文章: 北邮22信通:(7)实验1 题目四:一元多项式(节省内存版)_青山如…...

Fiddler抓取https史上最强教程
有任何疑问建议观看下面视频 2023最新Fiddler抓包工具实战,2小时精通十年技术!!!对于想抓取HTTPS的测试初学者来说,常用的工具就是fiddler。 但是初学时,大家对于fiddler如何抓取HTTPS难免走歪路ÿ…...
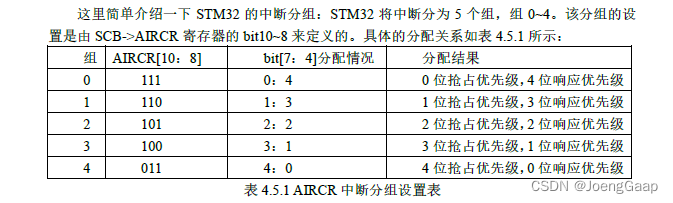
STM32开发基础知识入门
C语言基础 位操作 对基本类型变量可以在位级别进行操作。 1) 不改变其他位的值的状况下,对某几个位进行设值。 先对需要设置的位用&操作符进行清零操作,然后用|操作符设值。 2) 移位操作提高代码的可读性。 3) ~取反操作使用技巧 可用于对某…...

学习操作系统的必备教科书《操作系统:原理与实现》| 文末赠书4本
使用了6年的实时操作系统,是时候梳理一下它的知识点了 摘要: 本文简单介绍了博主学习操作系统的心路历程,同时还给大家总结了一下当下流行的几种实时操作系统,以及在工程中OSAL应该如何设计。希望对大家有所启发和帮助。 文章目录…...
)
大数据的常用算法(分类、回归分析、聚类、关联规则、神经网络方法、web数据挖掘)
在大数据时代,数据挖掘是最关键的工作。大数据的挖掘是从海量、不完全的、有噪声的、模糊的、随机的大型数据库中发现隐含在其中有价值的、潜在有用的信息和知识的过程,也是一种决策支持过程。其主要基于人工智能,机器学习,模式学…...
【数据结构】详解二叉树与堆与堆排序的关系
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...
【Pandas】数据分析入门
文章目录前言一、Pandas简介1.1 什么是Pandas1.2 Pandas应用二、Series结构2.1 Series简介2.2 基本使用三、DataFrame结构3.1 DataFrame简介3.2 基本使用四、Pandas-CSV4.1 CSV简介4.2 读取CSV文件4.3 数据处理五、数据清洗5.1 数据清洗的方法5.2 清洗案例总结前言 大家好&…...
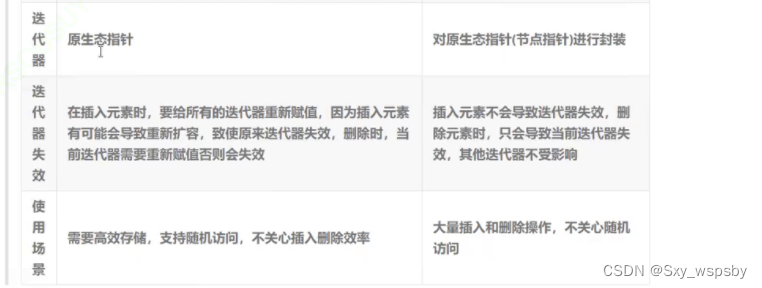
【c++】:list模拟实现“任意位置插入删除我最强ƪ(˘⌣˘)ʃ“
文章目录 前言一.list的基本功能的使用二.list的模拟实现总结前言 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中࿰…...

QT表格控件实例(Table Widget 、Table View)
欢迎小伙伴的点评✨✨,相互学习🚀🚀🚀 博主🧑🧑 本着开源的精神交流Qt开发的经验、将持续更新续章,为社区贡献博主自身的开源精神👩🚀 文章目录前言一、图示实例二、列…...

第二章Vue组件化编程
文章目录模块与组件、模块化与组件化模块组件模块化组件化Vue中的组件含义非单文件组件基本使用组件注意事项使用 kebab-case使用 PascalCase组件的嵌套模板templateVueComponent一个重要的内置功能单文件组件Vue脚手架使用Vue CLI脚手架先配置环境初始化脚手架分析脚手架结构实…...
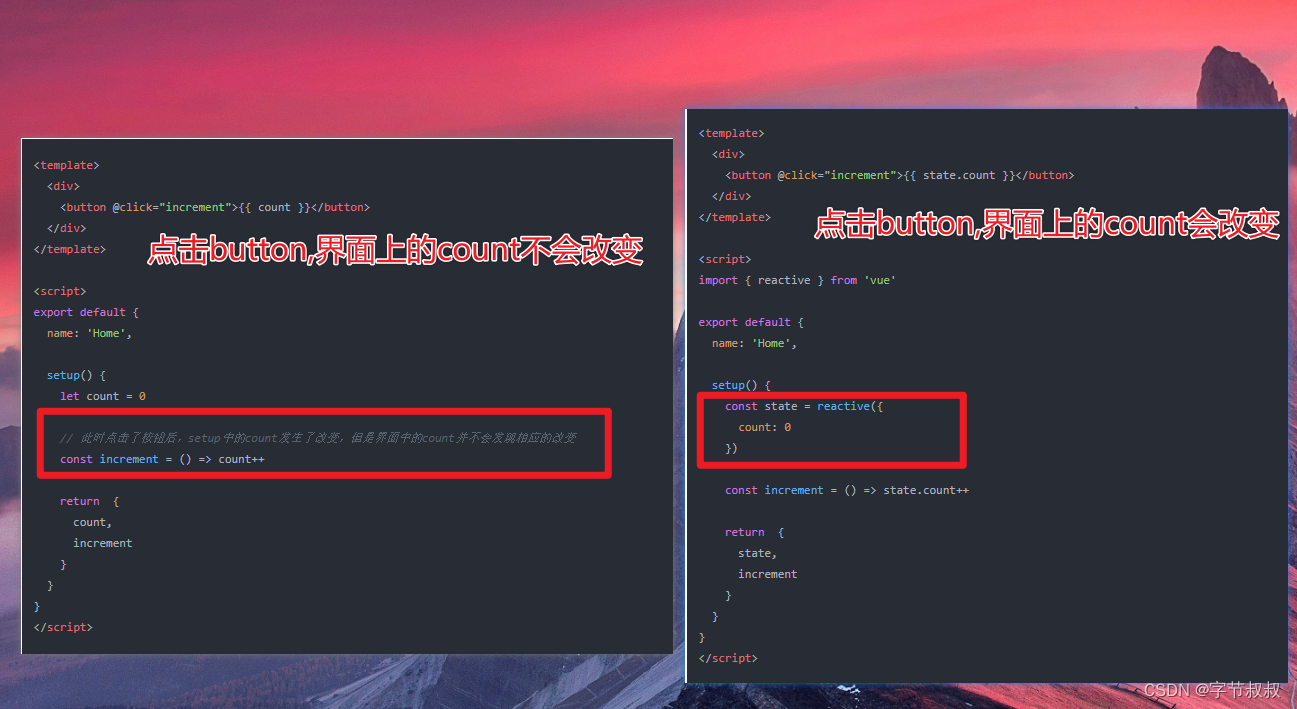
面试官:vue2和vue3的区别有哪些
目录 多根节点,fragment(碎片) Composition API reactive 函数是用来创建响应式对象 Ref toRef toRefs 去除了管道 v-model的prop 和 event 默认名称会更改 vue2写法 Vue 3写法 vue3组件需要使用v-model时的写法 其他语法 1. 创…...

【TopK问题】——用堆实现
文章目录一、TopK问题是什么二、解决方法三、时间复杂度一、TopK问题是什么 TopK问题就是从1000个数中找出前K个最大的数或者最小的数这样的类似问题。 不过并不要求这k个数字必须是有序的,如果题目有要求,则进行堆排序即可。 还有比如求出全国玩韩信…...

【Spring从成神到升仙系列 四】从源码分析 Spring 事务的来龙去脉
👏作者简介:大家好,我是爱敲代码的小黄,独角兽企业的Java开发工程师,CSDN博客专家,阿里云专家博主📕系列专栏:Java设计模式、数据结构和算法、Kafka从入门到成神、Kafka从成神到升仙…...

使用Nginx反向代理OpenAI API
由于OpenAI的API在国内无法访问,所以可以通过海外服务器利用Nginx实现反向代理。 安装Nginx 这一步就不赘述了,不同的Linux系统安装方式略有不同,根据自己的服务器的系统自行百度即可。 OpenSSL创建证书 因为OpenAI的接口是https协议的&a…...
)
USB键盘实现——字符串描述符(四)
字符串描述符 字符串描述符内容解析和 HID鼠标 一致。 获取字符串描述符请求 标准设备请求 typedef struct __attribute__ ((packed)){union {struct __attribute__ ((packed)) {uint8_t recipient : 5; ///< Recipient type usb_request_recipient_t.uint8_t type …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
