黑白格
题目描述
小杨有一个 n 行 m 列的网格图,其中每个格子要么是白色,要么是黑色。
小杨想知道至少包含 k 个黑色格子的最小子矩形包含了多少个格子。
输入格式
第一行包含三个正整数 n,m,k,含义如题面所示。
之后 n 行,每行⼀个长度为 m 的 01 串,代表网格图第 i 行格子的颜色,如果为 0,则对应格子为白色,否则为黑色。
输出格式
输出一个整数,代表至少包含 k 个黑色格子的最小子矩形包含格子的数量,如果不存在则输出 0。
输入输出样例
输入 #1
4 5 5 00000 01111 00011 00011
输出 #1
6
说明/提示
样例解释
对于样例 1,假设 (i,j) 代表第 i 行第 j 列,至少包含 5 个黑色格子的最小子矩形的四个顶点为 (2,4),(2,5),(4,4),(4,5),共包含 6 个格子。
数据范围
对于全部数据,保证有 1≤n,m≤100,1≤k≤n×m。
| 子任务编号 | 得分 | n,m |
|---|---|---|
| 1 | 20 | ≤10 |
| 2 | 40 | n=1,1≤m≤100 |
| 3 | 40 | ≤100 |
做法一:暴力
#include <iostream>
using namespace std;int s[110][110];
int main()
{int n,m,k;cin>>n>>m>>k;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){char c;cin>>c;s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+(c=='1');}int maxn=2e9;for(int r1=1;r1<=n;r1++)for(int r2=r1;r2<=n;r2++)for(int c1=1;c1<=m;c1++)for(int c2=c1;c2<=m;c2++){int area=(r2-r1+1)*(c2-c1+1);int b=s[r2][c2]-s[r1-1][c2]-s[r2][c1-1]+s[r1-1][c1-1];if(b>=k&&area<maxn)maxn=area;}cout<<(maxn<2e9?maxn:0);return 0;
}搞一个二位前缀和暴力,打擂台,无了,但是O(n⁴),这道题数据小能过。
---------------------------------------------------------------------------------------------------------------------------------
做法二:二分
#include <iostream>
using namespace std;int n,m,k,r1,r2,s[110][110];
int f(int a,int b,int c,int d)
{return s[b][d]-s[a-1][d]-s[b][c-1]+s[a-1][c-1];
}
bool check(int mid)
{for(int l=1;l+mid-1<=m;l++){int r=l+mid-1;int b=f(r1,r2,l,r);if(b>=k)return true;}return false;
}
int bs()
{int l=1,r=m;while(l<r){int mid=(l+r)/2;if(check(mid))r=mid;elsel=mid+1;}return l;
}
int main()
{cin>>n>>m>>k;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){char c;cin>>c;s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+(c=='1');}int minx=2e9;for(r1=1;r1<=n;r1++)for(r2=r1;r2<=n;r2++){if(f(r1,r2,1,m)<k)continue;int w=bs();int area=(r2-r1+1)*w;if(area<minx)minx=area;}cout<<(minx==2e9?0:minx);return 0;
}做法:
1.二层循环固定r1和r2。
2.二分查找,找宽度(即c1和c2差)。
3.check里枚举所有可能,有一个满足就return true。
4.二层循环*二分*check,复杂度O(n³logn)。
细节:
1.写一个f函数算二维区间和,简洁还能偷懒o(* ̄▽ ̄*)ブ
2.由于是二分,必须保证两头至少一个是true,不然会出错,所以要提前判断这个r1和r2的最大区间够不够k个,不够continue。
相关文章:

黑白格
题目描述 小杨有一个 n 行 m 列的网格图,其中每个格子要么是白色,要么是黑色。 小杨想知道至少包含 k 个黑色格子的最小子矩形包含了多少个格子。 输入格式 第一行包含三个正整数 n,m,k,含义如题面所示。 之后 n 行,每行⼀个…...

数据链路层(MAC地址)
文章目录 数据链路层(MAC地址)1、以太网2、以太网帧格式3、MAC地址4、对比理解 MAC 地址和 IP 地址5、最大传输单元(MTU)6、MTU 对 IP 协议的影响7、MTU 对 UDP 协议的影响8、MTU 对 TCP 协议的影响9、查看硬件地址和 MTU10、ARP …...

【ruby java】登陆功能/邮件发送模版240903
Rails 风格登录系统添加全面而详细的注释,解释每个部分的功能和用途。 详细注释,解释了每个文件和代码块的功能。以下是一些关键点的总结: 1. 控制器(Controllers): - ApplicationController: …...

告别格式不兼容烦恼!ape转换mp3,分享3个简单方法
各位读者们,你们是否有过这种体验:满怀期待地在网上下载一首好听的歌曲,结果怎么点击手机都播放不了,定睛一看,弹窗显示“无法播放该音频文件”。这是为什么呢?原来那首歌的音频格式是ape,不被手…...
Java核心知识体系-并发与多线程:线程基础
1 先导 Java线程基础主要包含如下知识点,相信我们再面试的过程中,经常会遇到类似的提问。 1、线程有哪几种状态? 线程之间如何转变? 2、线程有哪几种实现方式? 各优缺点? 3、线程的基本操作(线程管理机制ÿ…...
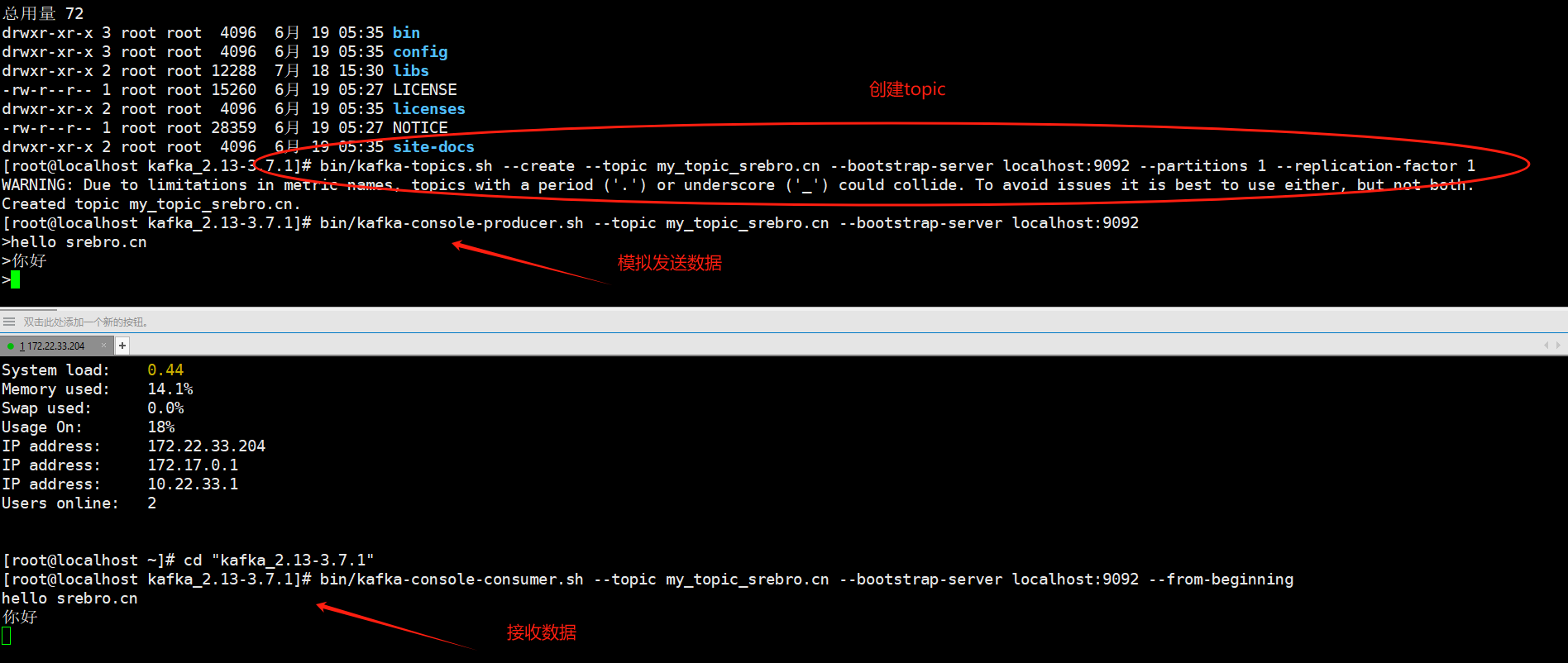
KRaft模式下的Kafka启动指南:摆脱Zookeeper依赖
一、背景介绍 多年来,人们一直在同时使用Apache ZooKeeper和Apache Kafka。但是自Apache Kafka 3.3发布以来,它就可以在没有ZooKeeper的情况下运行。同时它包含了新的命令kafka-metadata-quorum和kafka-metadata-shell?该如何安装新版kafka,…...

【数据库】MySQL-基础篇-函数
专栏文章索引:数据库 有问题可私聊:QQ:3375119339 目录 一、简介 二、字符串函数 三、数值函数 四、日期函数 五、流程函数 一、简介 函数 是指一段可以直接被另一段程序调用的程序或代码。 也就意味着,这一段程序或代码在 M…...

dp练习【4】
最长数对链 646. 最长数对链 给你一个由 n 个数对组成的数对数组 pairs ,其中 pairs[i] [lefti, righti] 且 lefti < righti 。 现在,我们定义一种 跟随 关系,当且仅当 b < c 时,数对 p2 [c, d] 才可以跟在 p1 [a, b…...

php 实现推荐算法
在PHP中实现推荐算法的应用场景通常包括电商、社交媒体、内容平台等。推荐算法可以帮助用户找到与其兴趣相关的内容,提高用户体验和平台黏性。以下是几种常见的推荐算法及其PHP实现方式: 1. 基于协同过滤的推荐算法 协同过滤(Collaborative…...
——光圈)
相机光学(三十六)——光圈
0.参考链接 (1)Hall光圈和Piris光圈的区别 (2)自动光圈及P-IRIS原理 1.光圈分类 Hall光圈和Piris光圈是两种不同的光圈技术。它们之间的区别如下: Hall光圈:Hall光圈是一种传统的光电子元件,通…...

数据结构——树和二叉树
目录 一、树的概念 二、树结点之间的关系 三、二叉树 1、满二叉树 2、完全二叉树 四、二叉树的存储 1、顺序存储 2、链式存储 一、树的概念 如果数据和数据之间满足一对多的关系,将其逻辑结构称之为树 如下图:树的根与树的分支存在一对多的关系 将上…...

142. Go操作Kafka(confluent-kafka-go库)
文章目录 Apache kafka简介开始使用Apache Kafka构建生产者构建消费者 总结 之前已经有两篇文章介绍过 Go如何操作 kafka 28.windows安装kafka,Go操作kafka示例(sarama库) 51.Go操作kafka示例(kafka-go库) Apache ka…...

spring boot(学习笔记第十九课)
spring boot(学习笔记第十九课) Spring boot的batch框架,以及Swagger3(OpenAPI)整合 学习内容: Spring boot的batch框架Spring boot的Swagger3(OpenAPI)整合 1. Spring boot batch框架 Spring Batch是什么 Spring Batch 是一个…...

docker安装 redis 并且加密开启SSL/TLS通道
拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest docker tag registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest redis:latest要在 Docker 容器中启动 Redis 并开启 SSL/TLS 加密,需按照以下步骤修改启动命令和配置…...

什么是ARM架构?什么是X86架构?两者的区别是什么?
一、什么是ARM架构 (一)起源于发展 ARM 架构由英国剑桥的 Acorn 计算机公司开发。因市场无合适产品,Acorn 自行设计出第一款微处理器,命名为 ARM。此后 ARM 架构不断发展,1990 年为与苹果合作成立 ARM 公司࿰…...
【vscode】vscode paste image插件设置
本文首发于 ❄️慕雪的寒舍 vscode编辑md文件的时候,如果想插入图片,自带的粘贴只会粘贴到当前目录下,也没有文件重命名,很不友好。 在扩展商店里面有mushan的Paste Image插件,相比自带的,更加友好一点。但…...

自定义string类
#include <iostream> #include <string> int main() { std::string str "Hello, World!"; // 使用 c_str() 将 std::string 转换为 C 风格字符串,并传递给 printf printf("The string is: %s\n", str.c_str()); // 尝试修改…...

Python | Leetcode Python题解之第387题字符串中的第一个唯一字符
题目: 题解: class Solution:def firstUniqChar(self, s: str) -> int:position dict()q collections.deque()n len(s)for i, ch in enumerate(s):if ch not in position:position[ch] iq.append((s[i], i))else:position[ch] -1while q and po…...

RocketMQ 消费时序列化报错问题分析及解决
问题背景 在2024年3月7日,系统消费 RocketMQ 消息时出现了序列化报错,错误信息显示为: java.io.InvalidClassException: com.xxx.xxx.bean.mg.GoodsChangeLogMessage; local class incompatible: stream classdesc serialVersionUID... 这是…...

全能与专精:探索未来AI模型的发展趋势与市场潜力
文章目录 每日一句正能量前言AI模型的全面评估和比较AI模型的专精化和可扩展性AI模型的合理使用和道德规范后记 每日一句正能量 一个人,如果没有经受过投资失败的痛楚,又怎么会看到绝望之后的海阔天空。很多时候,经历了人生中最艰难的事&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
