树与二叉树的存储与遍历
文章目录
- 一、树概念
- 二、二叉树
- 三、二叉树的存储与遍历
一、树概念
如前面的顺序表,链表,栈和队列都是线性的数据结构,树是非线性的结构。树可以有n个结点,n>=0,当n=0是就表示树为空
n>0,代表树不为空,不为空的树,它只有一个根结点,然后其余的结点又是构成互不相交的树,然后这些树本身又是一棵树,这些树且为根节点的子树。
任何一棵树都由两部分构成
1、根
2、子树
然后子树又由根和子树构成…无穷无尽的,直到为空为止,所以树又是递归定义的
根是唯一的但是它的子树有许多,莫得限制,且这些子树它们永远也不会相交。
树节点
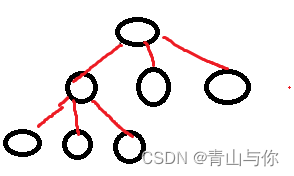
树是由许多结点构成的,那么每个结点又是啥样的嘞?树的每个结点它有可能会有子树,且它拥有子树的数量也是它该节点的度,那么整棵树的度为多大?,一颗树的度为该树内部结点的度的最大值
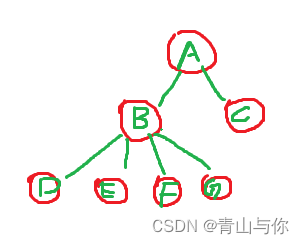
上述这颗树的度也是结点B的度,为4,然后就像D,E,F,G,C,这些结点它后面没有子树了,也就是度为0的结点,这些结点也有另一个名字:
叶子结点,然后嘞像B结点为非叶子结点。
节点关系
然后这些结点之间有什么关系?
这些结点它的子树的根也叫做它的孩子,然后这个结点也是它孩子结点的双亲
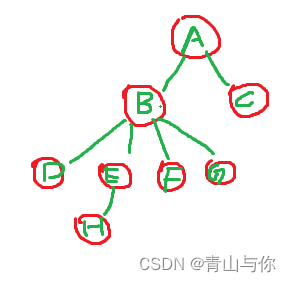
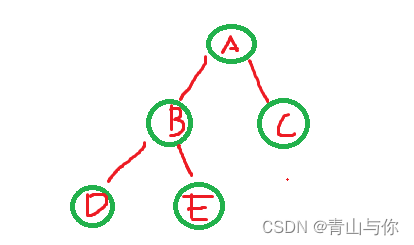
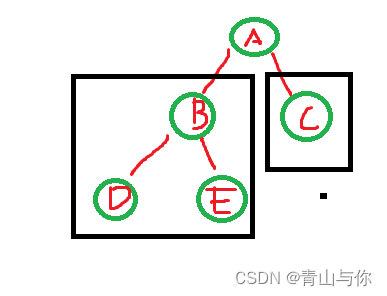
如结点A
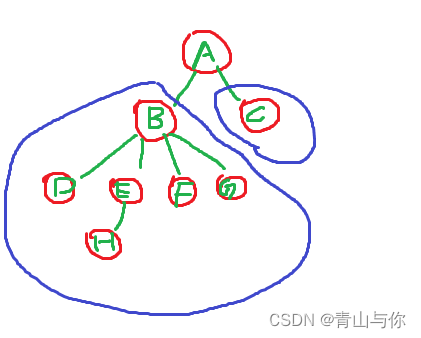
蓝颜色圈起来的为它的子树,然后这些子树的根B,C又为A结点的孩子,然后嘞A也是它两个孩子结点的双亲结点,如A结点是B和C结点的双亲,B,C结点为A的孩子那么B,C它们两个结点之间又是什么关系?它们有同一个双亲,那么有同一个双亲在我们现实生活中难道不是兄弟吗,没错在树中有同一个双亲结点的孩子结点它们之间互为兄弟关系,称为兄弟结点。其实这些关系是借鉴生活中对应的家庭中的关系
树高度
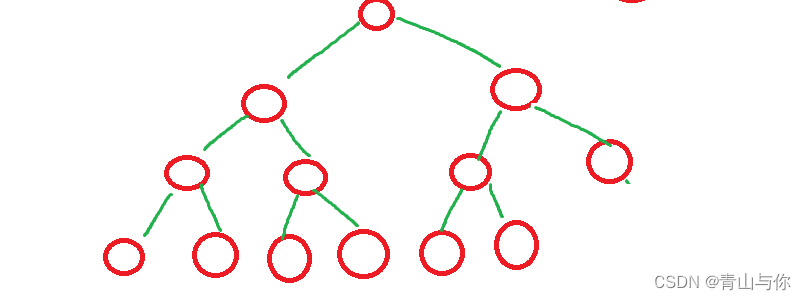
树的高度也叫树的层次,树的根结点所在为第一层,然后它的孩子为第二层
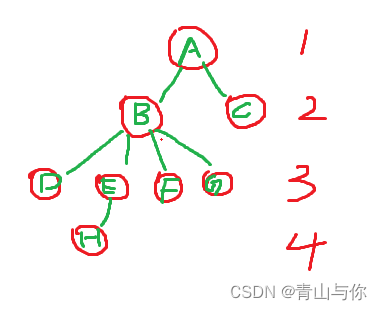
这颗树高度为4,如果给定某个结点在第h层,那么它的孩子结点在第h+1层
树的存储
由于每个节点的孩子可以有很多个,根本不知道它的孩子节点有多少个,除非树中已经明确给出了树的度为n,那么就可以定义n个孩子节点
但是如果不知道度为多少,应该如何定义树?
有一种存储方式很适合树结构表示:左孩子又兄弟表示法
typedef int TDataType;
typedef struct BTNode
{struct BTNode* leftchild;//指向根节点的左孩子struct BTNode* rightbrother;//指向左孩子它的右兄弟TDataType data;
}BTNode;
这种方法好处是不管该节点有多少孩子节点,都只需要知道它的左孩子然后就可以找到它其他的孩子节点,不论怎样都只有两个指针
A的右兄弟为空然后A有两个孩子,但是他不会管他自己有多少孩子节点,它只需要找到它的左孩子,然后再通过它的左孩子就可以找到它的右孩子了。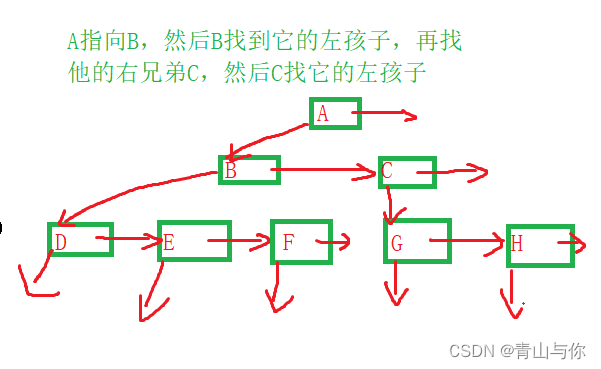
通过每一颗子树的根找到它的左孩子,然后再找左孩子的右兄弟,这个只有两个指针,感觉上像是二叉树,但是并不是,二叉树一个节点最多只有两个孩子,但是这里一个节点可以有多个孩子节点
不管有多少个孩子都只需要找第一个孩子,然后剩下的用兄弟指针去链接,每个节点都是两个指针,这点有些像二叉树,那么下面就引入二叉树
二、二叉树
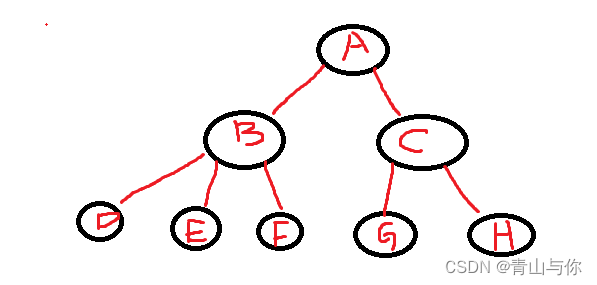
二叉树就是树的度不大于2,也就是每个结点它的孩子结点不超过两个,每个结点的子树不超过两棵,然后在左边的那个结点为左孩子,右边的结点为右孩子。每一棵二叉树由根,左子树,右子树构成。二叉树也具有树的基本特性
左边的为左子树,右边的为右子树 二叉树可以为空,也可以只有一个节点(根),亦可以只有左子树或者只有右子树,还可以左子树和右子树都有
但是二叉树中有两个特殊的树
二叉树又有几种特殊的
- 满二叉树
- 完全二叉树
满二叉树叶子结点在同一层上且叶子结点只出现在最后一层,非叶子结点的度一定为2,就是每一层都是满的,那么高度为h的满二叉树有多少的节点?
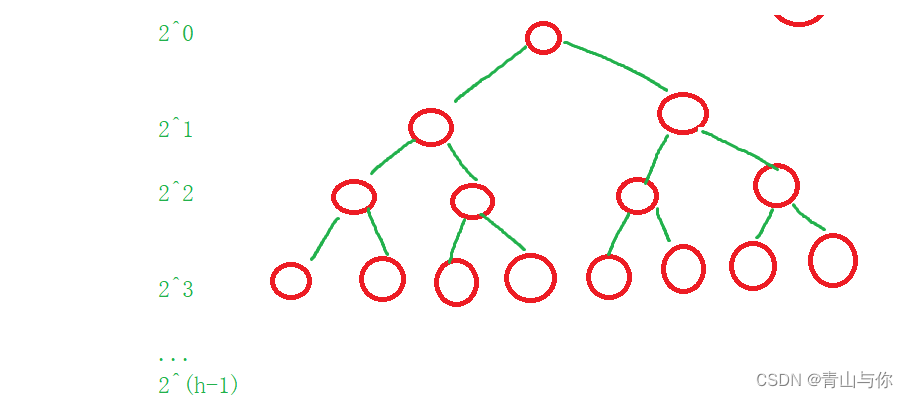
每一层节点个数相加可以发现是一个等比数列,节点个数也就是等比数列求和为 2^h - 1
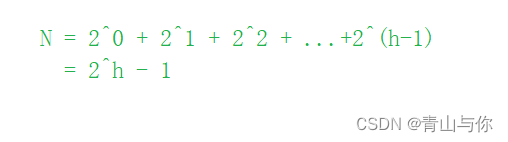
那么假设满二叉树有N个节点,求其高度h

由于log2(N-1)算出的结果很大程度上可能是小数,但是高度一般用整数表示,那么以得到的值向下取整得到整数然后再加一就为满二叉树的高度
还有就是同普通二叉树相比满二叉树的结点个数是最多的.
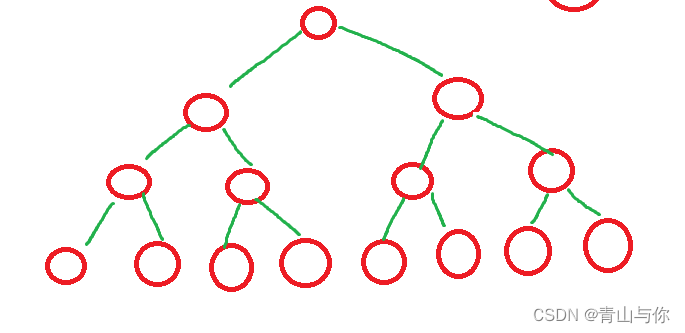
完全二叉树
如果二叉树有h层,那么它的前h-1层都是满的,最后一层不一定满但是要求最后一层从左到右是连续的
那么假设完全二叉树高度为h的节点数量的范围是多少?
N ~[log^(h-1)^,log^h^-1]最少前h-1层是满的第h层只有一个节点,最多也就是一棵满二叉树
任意一棵二叉树
它的叶子结点数一定比度为2的结点数目多一个,即假设叶子结点数为n0,度为2的结点数为n2,那么n0=n2+1;
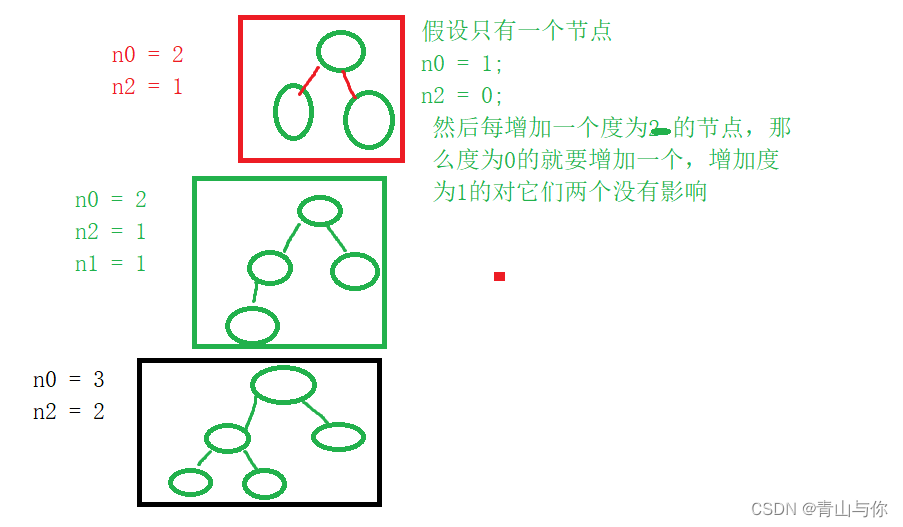
且完全二叉树中度为1的节点最多只有一个,或者就是没有度为1的节点,因为其是连续的,最多只会缺少右孩子
三、二叉树的存储与遍历
二叉树的存储
二叉树用数组存储容易会造成空间上的浪费,如果二叉树只有左子树或者右子树
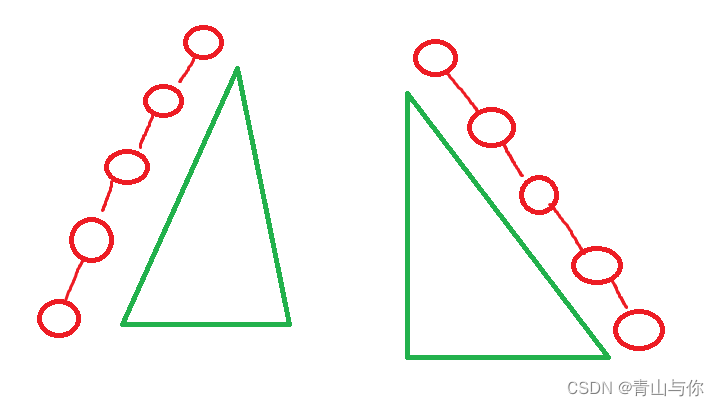
绿色部分那片内存空间浪费了,没有被使用,因此用链式存储结构较为合适
但是如果是一棵完全二叉树的话,用顺序存储结构就较好了,因为完全二叉树是连续的
二叉树链式存储结构
typedef int TDataType;
typedef struct BTNode
{struct BTNode* left;struct BTNode* right;TDataType data;
}BTNode;
一个指针指向它的左孩子,一个指针指向右孩子
二叉树遍历
二叉树遍历方式主要有四种,但是我这里先分享三种遍历方式
- 前序遍历
- 中序遍历
- 后序遍历
先手动构建二叉树的节点
BTree* BuyNode(TDataType x)
{BTree* newnode = (BTree*)malloc(sizeof(BTree));if (newnode == NULL){perror("malloc fail\n");return NULL;}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}
然后再自己创建一棵二叉树叭
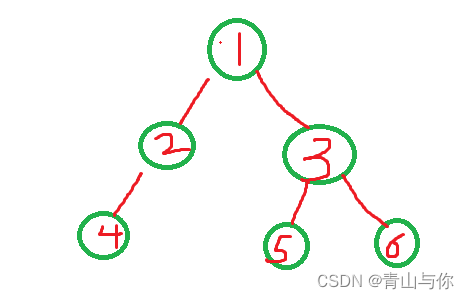
BTree* BTCreat()
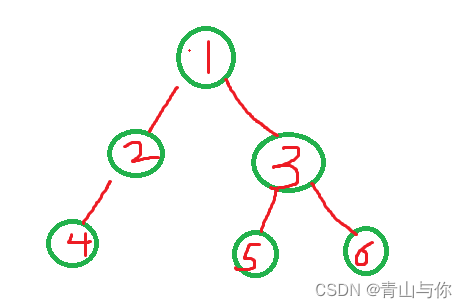
{BTree* newnode1 = BuyNode(1);BTree* newnode2 = BuyNode(2);BTree* newnode3 = BuyNode(3);BTree* newnode4 = BuyNode(4);BTree* newnode5 = BuyNode(5);BTree* newnode6 = BuyNode(6);newnode1->left = newnode2;newnode1->right = newnode3;newnode2->left = newnode4;newnode2->right = NULL;newnode3->left = newnode5;newnode3->right = newnode6;newnode5->left = NULL;newnode5->right = NULL;newnode6->left = NULL;newnode6->right = NULL;return newnode1;
}前序遍历
前序遍历究竟是如何遍历二叉树的呢?
由于一棵二叉树由三部分构成:根、左子树、右子树
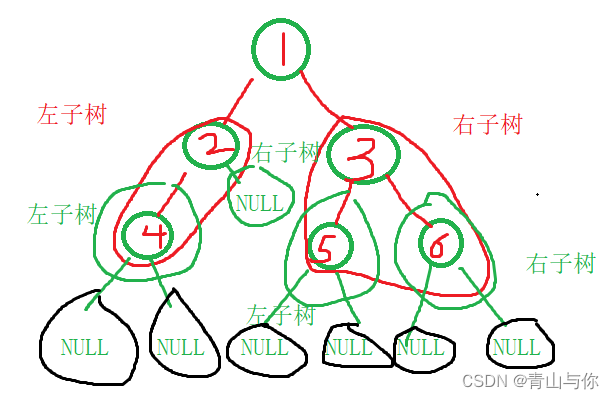
每一棵子树可以拆分为三部分,一直拆,直到子树为空就不可再拆分了
如果一棵二叉树是空,那么直接返回空,否则就是先访问这棵二叉树的根节点,然后再前序遍历它的左子树,它的左子树又是先访问它的根,然后又是左子树,当它的左子树以前序遍历访问直到空之后再以同样的前序遍历访问它的右子树,而它的右子树又是先遍历它的左子树依此直到为空,可以观察到访问是递归的,
前序遍历就是先访问其根,然后递归访问它的左子树,而左子树又由根,左子树,右子树,每一棵子树都由根,左子树,右子树构成,以前序遍历访问下去直到访问到空则返回然后访问它的右子树,右子树为空再返回,回溯了访问它双亲结点的右子树,最后回溯到整棵树的根,然后开始遍历访问整棵树的右子树,访问它的右子树时同样遵循先访问根,再访问左子树,最后访问右子树,遇到空则开始返回回溯
先访问 1,然后走它的左子树2,而它的左子树2又有根,左子树,右子树,访问2,然后再走它的左子树4,访问4,然后走4的左子树,4的左子树为空,代表4的左子树走完了,那么走它的右子树,它的右子树也为空,那么以4为子树作为2的左子树走完了,这回开始走2的右子树,2的右子树为空,那么就代表以2为子树作为1的左子树走完了,这回开始走1的右子树。
而1的右子树3不为空,又开始先访问3,然后走3的左子树5,访问5,然后走5的左子树,5的左子树走完了就代表以5为子树作为3的左子树走完了开始走3为子树它的右子树6不为空,访问6再走它的左子树,右子树最后就是全部都访问完了
这里前序我是将其空都算上的便于理解
前序 1 2 4 NULL NULL NULL 3 5 NULL NULL 6 NULL NULL
每一棵树都是由根,左子树,右子树构成
void PreOrder(BTree* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}前序遍历递归展开图
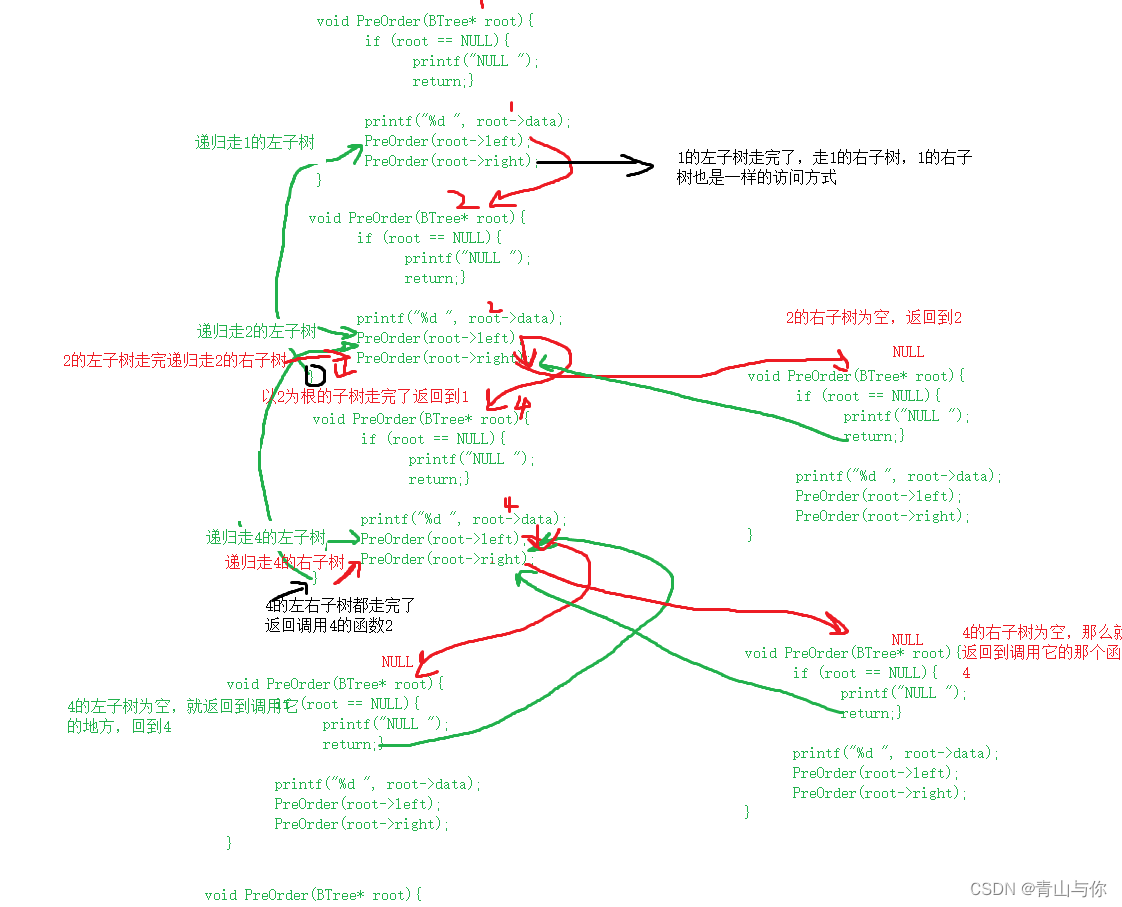
右子树也是一样的展开
中序和后序遍历的展开图这里就不再画了
中序遍历先访问左子树、再根、最后右子树
//中序遍历先访问每颗子树的左子树,直到左子树为空,才返回然后访问根,然后再访问以这个根为子树的右子树,右子树又访问其左子树,
//若干个子问题,一直拆,每棵树又由根,右子树,左子树三部分构成
//在中序遍历时要先访问每颗子树的左子树,直到以它为根的左子树为空,才访问它然后再访问其右子树//每访问一次子树都是一次函数调用,且每一次函数调用都开辟一个函数栈帧用来维护这次函数栈帧开辟的空间,且每次返回时函数栈帧弹出,函数栈帧跳到调用它的
//那个函数以维护它的栈帧空间,且函数调用使用空间是允许重复的,即一次函数调用返回之后这块空间回收给操作系统然后下一次再调用其他函数
//又可以用这块内存空间
void InOrder(BTree* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
中序 NULL 4 NULL 2 NULL 1 NULL 5 NULL 3 NULL 6 NULL
后序遍历先访问左子树、再右子树,最后访问根
//先访问根的左子树,然后再访问右子树最后访问根
// 左子树又拆分为根左子树右子树然后又先访问左子树,后右子树最后根
// 直到那颗子树左右子树都为空然后就访问它(根),然后回溯到它的双亲结点,以该双亲节点为根再访问它的右子树,
// 它的右子树又是先访问它的左子树,然后右子树最后根
// 最后直到根的左子树访问完了之后再访问右子树,最后再访问根
// 其实都是访问以每一颗子树为根的节点,只是时机不同
//
void PosOrder(BTree* root)
{if (root == NULL){printf("NULL ");return;}PosOrder(root->left);PosOrder(root->right);printf("%d ", root->data);
}
后序 NULL NULL 4 NULL 2 NULL NULL 5 NULL NULL 6 3 1
今天的树与二叉树就基本概念分享到这里了,各位再见。
相关文章:

树与二叉树的存储与遍历
文章目录一、树概念二、二叉树三、二叉树的存储与遍历一、树概念 如前面的顺序表,链表,栈和队列都是线性的数据结构,树是非线性的结构。树可以有n个结点,n>0,当n0是就表示树为空 n>0,代表树不为空,不为空的树&am…...

28-队列练习-LeetCode622设计循环队列
题目 设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。 循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通…...

你值得拥有——流星雨下的告白(Python实现)
目录1 前言2 霍金说移民外太空3 浪漫的流星雨展示 4 Python代码 1 前言我们先给个小故事,提一下大家兴趣;然后我给出论据,得出结论。最后再浪漫的流星雨表白代码奉上,还有我自创的一首诗。开始啦:2 霍金说移民外太空霍…...

【5G RRC】NR测量事件介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

PMP项管2023年5月的备考准备攻略!
2023年共有4次PMP考试,分别是3月、5月、8月、11月,由于3月份考试不开放新报名,所以第一次备考PMP的同学可以选择参加5月份考试。那么,现在备考5月份PMP考试还来得及吗? 现在开始备考5月PMP考试,时间是非常…...
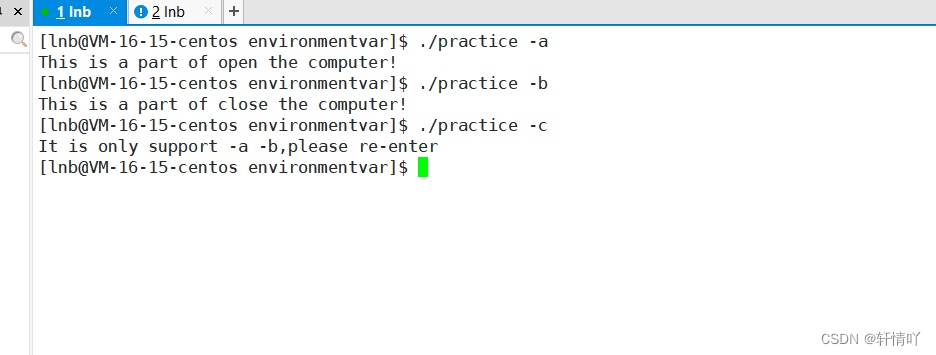
Linux进程概念—环境变量
Linux进程概念—环境变量1.孤儿进程2.环境变量2.1常见环境变量2.2查看环境变量方法2.3在环境变量中添加2.4和环境变量相关的命令2.5环境变量的组织方式2.6命令行参数🌟🌟hello,各位读者大大们你们好呀🌟🌟 Ὠ…...

用JS+CSS打造你自己的弹幕王国,让网页动起来!
文章目录前言主要内容实现方法DOM方法显现效果代码CANVAS方法显现效果代码总结更多宝藏前言 😎🥳😎🤠😮🤖🙈💭🍳🍱 用JSCSS打造你自己的弹幕王国,…...
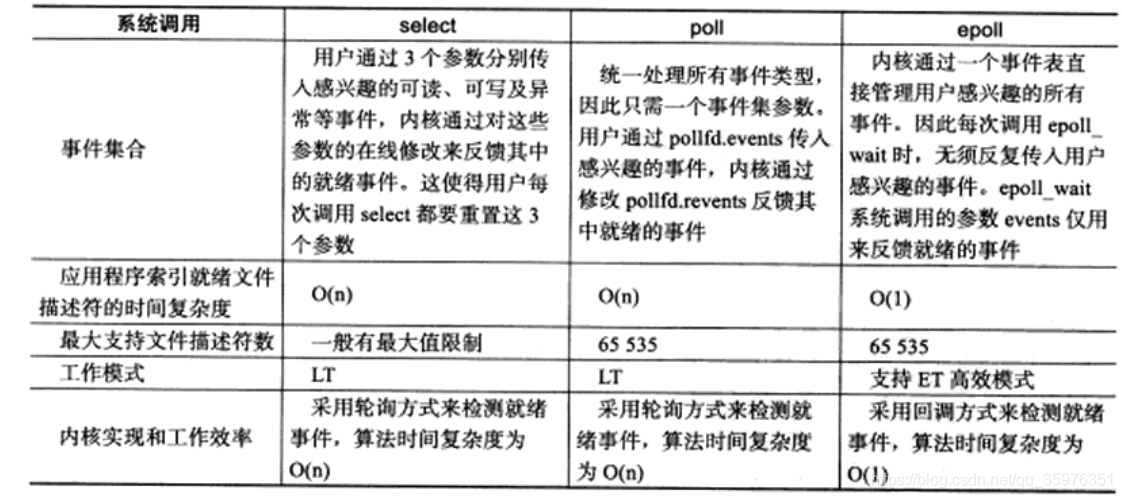
C++ LinuxWebServer 2万7千字的面经长文(上)
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 前言 Linux Web Server项目虽然是现在C求职者的人手一个的项目,但是想要吃透这个项目ÿ…...

vue3 解决各场景 loading过度 ,避免白屏尴尬!
Ⅰ、前言 当我们每次打卡页面,切换路由,甚至于异步组件,都会有一个等待的时间 ;为了不白屏,提高用户体验,添加一个 loading 过度动画是 非常 常见的 ;那么这几种场景我们应该把 loading 加在哪…...

基于sringboot和小程序实现高校食堂移动预约点餐系统演示【源码】
基于sringboot实现高校食堂移动预约点餐系统演示开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件&am…...

开源操作系统与Windows大比拼!
科技网站ZDNet近日撰文称,在一个用户为王的时代,操作系统们为了获得青睐都放下了身段,采用免费策略,但其中却有一个例外——Windows 10。这样的一反常理让许多人不看好Windows的未来,难道这个我们最熟悉的朋友真的会成…...
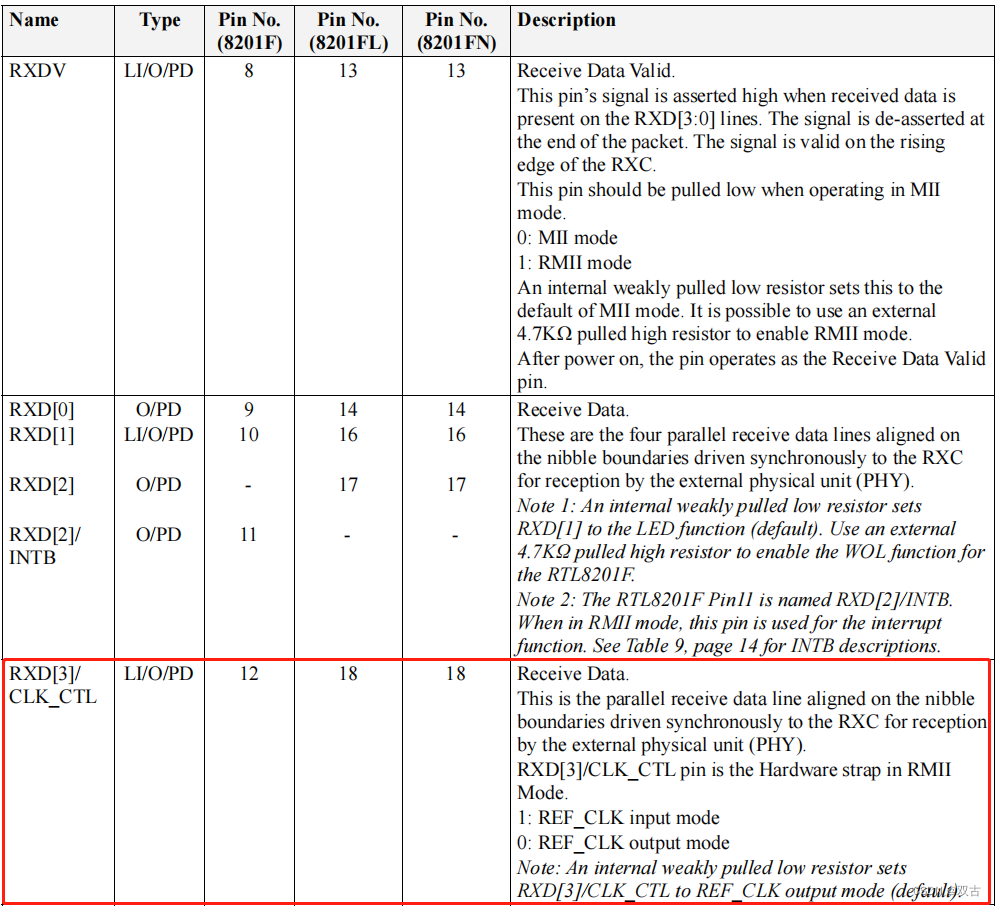
RTL8201 以太网PHY芯片 调试记录
一、概述 为了尽量给甲方降低成本,决定使用较低成本的PHY芯片RTL8201F-VB-CG芯片。移植官网的以太网demo程序,git上下载了一份很好看的rtl8201F的驱动程序,用来替换官方demo的lan8742程序。并没有直接通,于是开始了调试之路。 二…...
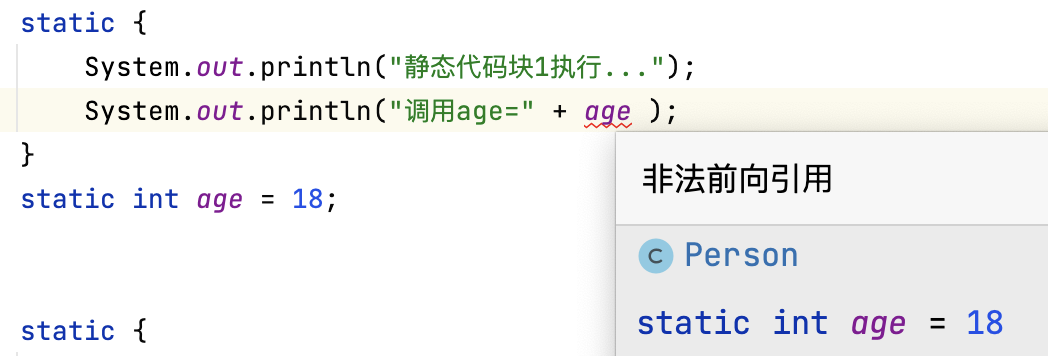
Java中Static关键字的五种用法详解
Static的五种用法大致如下: 修饰成员变量,使其成为类变量,也叫静态变量修饰成员方法,使其成为类方法修饰内部类,使其成为静态内部类静态代码块静态导包 直接一点,static关键字就是把属性和方法变为类相关&…...
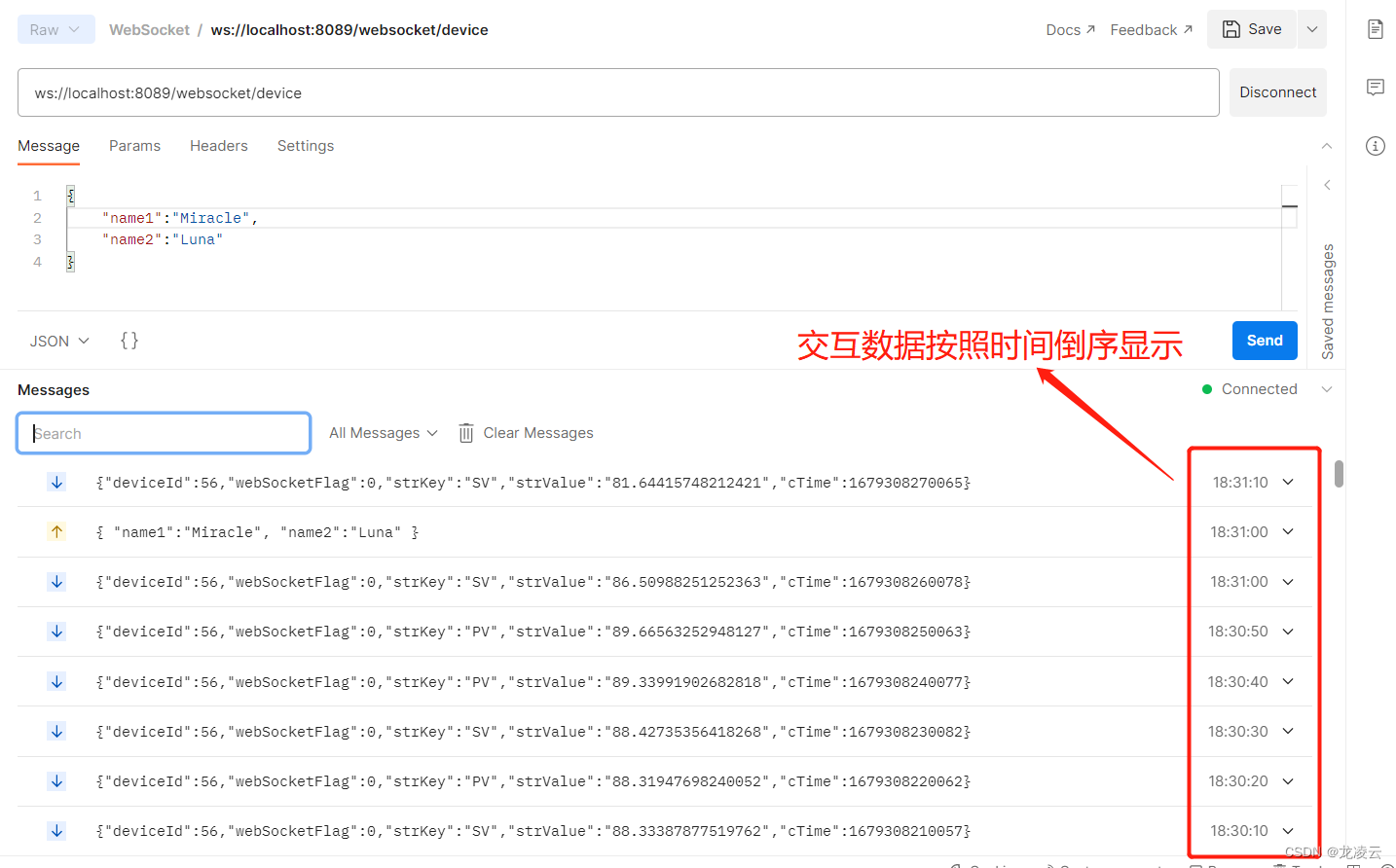
WebSocket 测试工具
一、WebSocket 简介 WebSocket是一种在单个TCP连接上进行全双工通信的协议。 WebSocket使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。在WebSocket API中,浏览器和服务器只需要完成一次握手,两者之间就直…...

低代码开发的未来~
IT 团队依靠笨重的软件开发流程和劳动密集型的手工编码来构建有形、可靠和现代应用程序的时代即将结束。随着新自动化技术的兴起、渴望创新的客户和最终用户的期望和需求迅速提高以及开发人员的短缺,软件行业被迫寻求替代方法,不仅提供服务和产品&#x…...
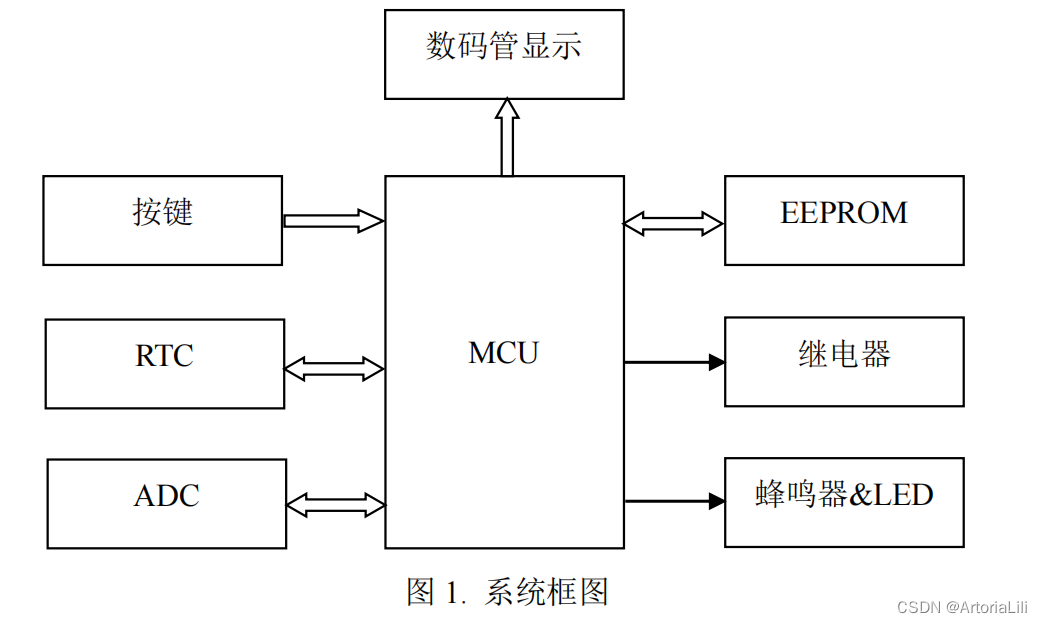
蓝桥杯真题——模拟灌溉系统
尽量每天都自己写一遍模板,记住模板就好写了 以下内容直接在模板内进行 基本任务:要求“模拟智能灌溉系统”能够实现土壤湿度测量、土壤湿度和时间显示、湿度阈值设 定及存储等基本功能。通过电位器 Rb2 输出电压信号,模拟湿度传感器输出信号…...

【数据结构】双向链表实现
Yan-英杰的主页 悟已往之不谏 知来者之可追 C程序员,2024届电子信息研究生 目录 一、什么是双向链表 二、双向链表的实现 一、什么是双向链表 双向链表也叫双链表,是链表的一种,它的每个数据节点中都有两个指针,分别指向直接后…...
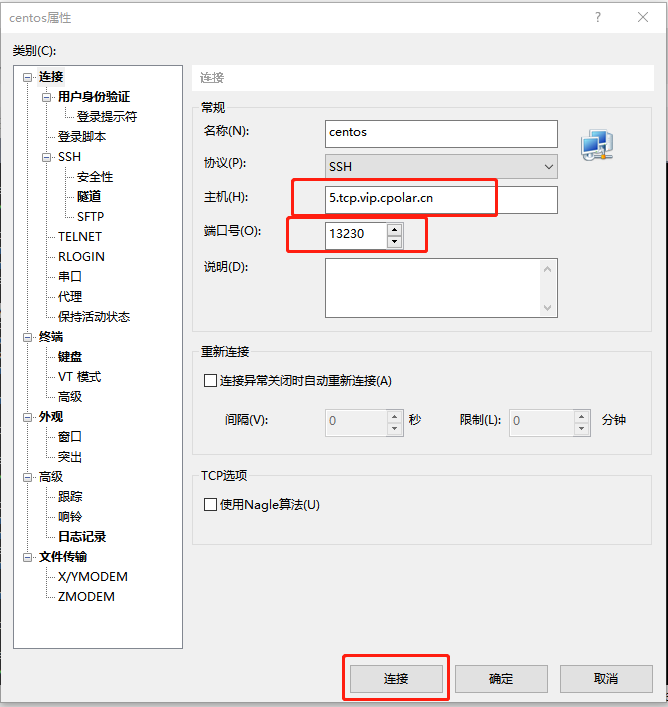
无公网IP,SSH远程连接Linux CentOS服务器【内网穿透】
文章目录1. Linux CentOS安装cpolar2. 创建TCP隧道3. 随机地址公网远程连接4. 固定TCP地址5. 使用固定公网TCP地址SSH远程本次教程我们来实现如何在外公网环境下,SSH远程连接家里/公司的Linux CentOS服务器,无需公网IP,也不需要设置路由器。 …...
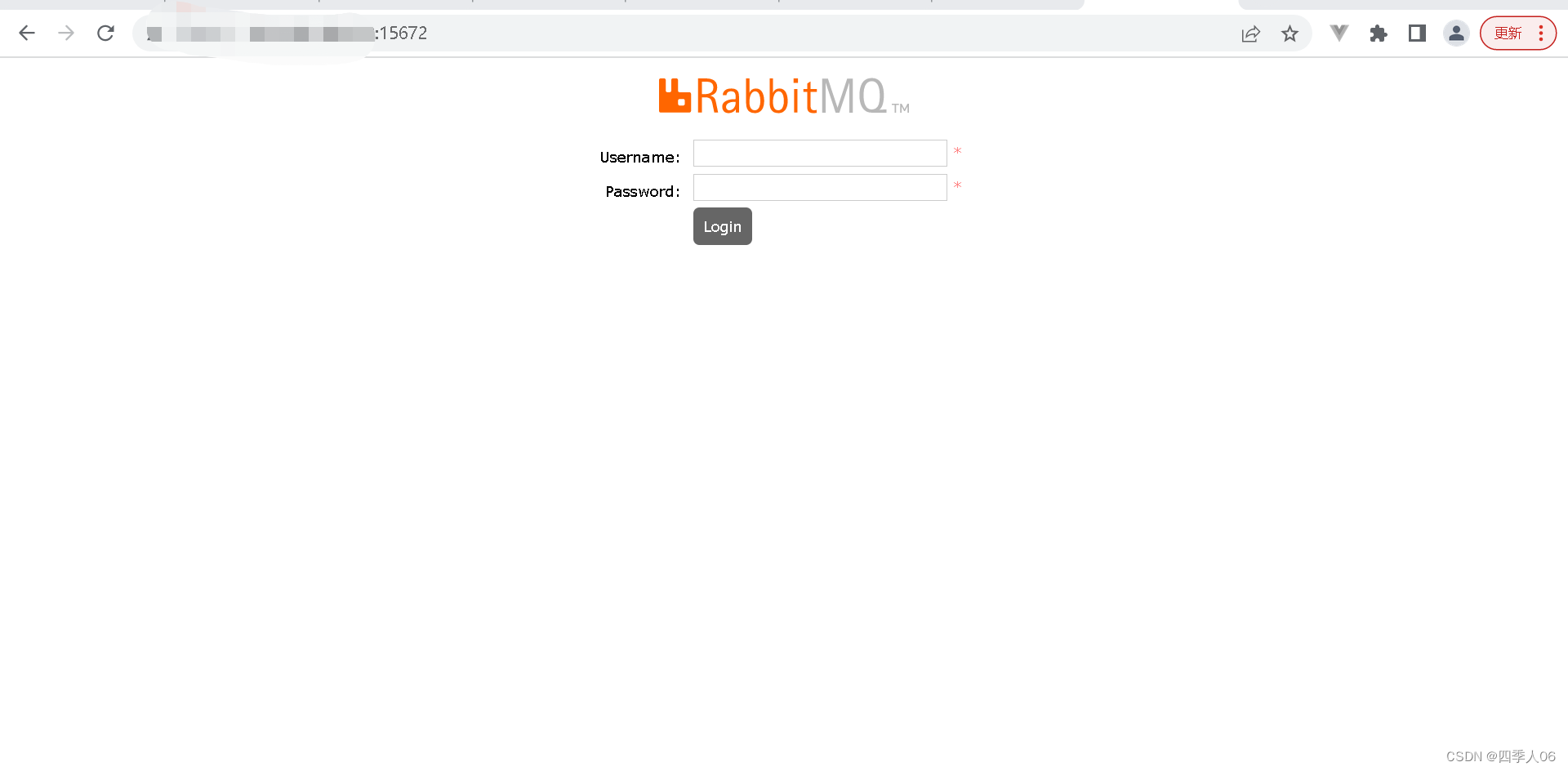
CentOS 7+Docker搭建rabbitMQ无法访问15672端口
CentOS 7Docker搭建rabbitMQ无法访问15672端口 1.我拉取的镜像自带管理UI界面 所以不可能是没有开启管理UI界面的原因 2.防火墙关闭状态 所以也不是防火墙的问题 3.在虚拟机本机localhost:15672也访问不了 4.端口监听是正常的 5.最后发现我容器内curl能够通,容…...
面试官:如何保证接口幂等性?一口气说了9种方法!
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址 大家好,我是大彬~ 今…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...