蓝桥杯真题2
[蓝桥杯 2013 省 B] 连号区间数
题目描述
小明这些天一直在思考这样一个奇怪而有趣的问题:
在 111 ~ NNN 的某个全排列中有多少个连号区间呢?这里所说的连号区间的定义是:
如果区间 [L,R][L, R][L,R] 里的所有元素(即此排列的第 LLL个到第 RRR 个元素)递增排序后能得到一个长度为 R−L+1R-L+1R−L+1 的“连续”数列,则称这个区间连号区间。
当 NNN 很小的时候,小明可以很快地算出答案,但是当 NNN 变大的时候,问题就不是那么简单了,现在小明需要你的帮助。
输入格式
第一行是一个正整数 N(1≤N≤50000)N (1 \le N \le 50000)N(1≤N≤50000), 表示全排列的规模。
第二行是 NNN 个不同的数字 Pi(1≤Pi≤N)P_i(1 \le P_i \le N)Pi(1≤Pi≤N), 表示这 NNN 个数字的某一全排列。
输出格式
输出一个整数,表示不同连号区间的数目。
样例 #1
样例输入 #1
4
3 2 4 1
样例输出 #1
7
样例 #2
样例输入 #2
5
3 4 2 5 1
样例输出 #2
9
提示
第一个用例中,有 777 个连号区间分别是:[1,1][1,1][1,1], [1,2][1,2][1,2], [1,3][1,3][1,3], [1,4][1,4][1,4], [2,2][2,2][2,2], [3,3][3,3][3,3], [4,4][4,4][4,4]。
第二个用例中,有 999 个连号区间分别是:[1,1][1,1][1,1], [1,2][1,2][1,2], [1,3][1,3][1,3], [1,4][1,4][1,4], [1,5][1,5][1,5], [2,2][2,2][2,2], [3,3][3,3][3,3], [4,4][4,4][4,4], [5,5][5,5][5,5]。
原题时限 5 秒, 64M。蓝桥杯 2013 年第四届省赛
分析
题目要求的是连续号区间数,因为这个题目的数据有个特点,就是数据不重复,所以如果说某个区间是连续的,那么这个区间的最大值-最小数必须等于下标差即(max-min==b-a)如果满足这个,则说明(a,b)为连续区间,将res++即可。那么如何求取每个区间的最大和最小值呢,我们不妨定下l,不断地去枚举r,这样我们只需要每次比较最大最小值和新加入元素的大小即可。
代码实现
import java.util.*;
public class Main{static int N = 10010;static int[] a = new int[N];public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();for(int i = 1; i <= n;i++) a[i]=scan.nextInt();int res = 0;for(int i = 1;i <= n;i++){int minv = Integer.MAX_VALUE;int maxv = Integer.MIN_VALUE;for(int j = i;j <= n;j++){minv = Math.min(minv, a[j]);maxv = Math.max(maxv, a[j]);if(maxv - minv == j - i) res ++;}}System.out.println(res);}
}
[蓝桥杯 2015 省 A] 饮料换购
题目描述
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊 C 型饮料,凭 333 个瓶盖可以再换一瓶 C 型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的 nnn 瓶饮料,最后他一共能喝到多少瓶饮料。
输入格式
一个整数 nnn,表示开始购买的饮料数量。(0<n<100000<n<100000<n<10000)
输出格式
一个整数,表示实际得到的饮料数。
样例 #1
样例输入 #1
100
样例输出 #1
149
样例 #2
样例输入 #2
101
样例输出 #2
151
提示
2015 年蓝桥杯省赛 A 组 H 题。
分析
这道题主要是要求思路清晰,直接去算就可以,先喝完手中的饮料,res+=n,剩下n个瓶盖,三个饮料盖可以换一瓶饮料,那么我们就又可以喝n/3瓶饮料,每次我们喝过饮料后会剩下 n/3+n%3个瓶盖,我们只需要不断重复过程,直至n<3
代码实现
import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int res = n;while(n>=3){res+=n/3;n = n / 3 + n%3;}System.out.println(res);}
}
[蓝桥杯 2014 省 AB] 地宫取宝
题目描述
X 国王有一个地宫宝库。是 n×mn \times mn×m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是 kkk 件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这 kkk 件宝贝。
输入格式
输入一行 333 个整数,用空格分开:nnn,mmm,k(1≤n,m≤50,1≤k≤12)k(1 \le n,m \le 50,1 \le k \le 12)k(1≤n,m≤50,1≤k≤12)。
接下来有 nnn 行数据,每行有 mmm 个整数 Ci(0≤Ci≤12)C_i(0 \le C_i \le 12)Ci(0≤Ci≤12) 代表这个格子上的宝物的价值。
输出格式
要求输出一个整数,表示正好取 kkk 个宝贝的行动方案数。该数字可能很大,输出它对 1000000007(109+7)1000000007(10^9+7)1000000007(109+7) 取模的结果。
样例 #1
样例输入 #1
2 2 2
1 2
2 1
样例输出 #1
2
样例 #2
样例输入 #2
2 3 2
1 2 3
2 1 5
样例输出 #2
14
提示
时限 1 秒, 256M。蓝桥杯 2014 年第五届省赛
分析
很明显的dp问题,我们将每个状态划分:
当走到某个格子上的时候:
(1)如果格子上宝贝的价值大于已有宝贝的最大值,那么可以选择拿或者不拿
(2)如果格子上宝贝的价值小于或者等于已有宝贝的最大值,那么只能选择不拿。
必须从左上角走到右下角,且只要到达右下角时物品个数满足条件即算一种方案。
只能选择向下或者向右走
不是必须到出口时,宝贝数量恰好满足条件,而是可以在任意位置就宝贝数量就可以满足条件,只需保证到达出口时宝贝数量仍然满足条件即可
import java.util.Scanner;public class Main {public static void main(String[] args) {int N = 55;int w[][] = new int[N][N];int f[][][][] = new int[N][N][13][14];//所有从起点走到(i, j),且已经取了k件物品,且最后一件物品的价值是C的合法方案的集合。int mod = 1000000007;Scanner sc = new Scanner(System.in);int n = sc.nextInt();int m = sc.nextInt();int k = sc.nextInt();for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {w[i][j] = sc.nextInt();w[i][j]++;//为了初始化,因为最终统计的是方法数}}f[1][1][1][w[1][1]] = 1;f[1][1][0][0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if(i==1 && j==1) continue;for (int u = 0; u <= k; u++) {for (int v = 0; v <= 13; v++) {f[i][j][u][v] = (f[i][j][u][v]+f[i-1][j][u][v])%mod;//最后一步是从上往下走,并且不取这个宝贝f[i][j][u][v] = (f[i][j][u][v]+f[i][j-1][u][v])%mod;//最后一步是从左往右走,并且不取这个宝贝if(u>0 && v==w[i][j])当前的方案数量=上一步的所有价值的方案数量之和{for (int c = 0; c < v; c++) {f[i][j][u][v] = (f[i][j][u][v] + f[i-1][j][u-1][c])%mod;//最后一步是从上往下走,并且取这个宝贝f[i][j][u][v] = (f[i][j][u][v] + f[i][j-1][u-1][c])%mod;//最后一步是从左往右走,并且不取这个宝贝}}}}}}int res = 0;for (int i = 0; i <= 13; i++) {res = (res + f[n][m][k][i])%mod;}System.out.println(res);}
}
相关文章:

蓝桥杯真题2
[蓝桥杯 2013 省 B] 连号区间数 题目描述 小明这些天一直在思考这样一个奇怪而有趣的问题: 在 111 ~ NNN 的某个全排列中有多少个连号区间呢?这里所说的连号区间的定义是: 如果区间 [L,R][L, R][L,R] 里的所有元素(即此排列的…...

PWM互补输出,以及死区时间计算
本文基于野火例程进行解说 实验内容 本次实验输出一对互补的pwm波,且进行死区时间的计算说明。 代码 互补输出对应的定时器初始化代码: bsp_advance_tim.c /********************************************************************************* fi…...

基于深度学习的海洋动物检测系统(Python+YOLOv5+清新界面)
摘要:基于深度学习的海洋动物检测系统使用深度学习技术检测常见海洋动物,识别图片、视频和实时视频中的海洋动物,方便记录、展示和保存结果。本文详细介绍海洋动物检测系统,在介绍算法原理的同时,给出Python的实现代码…...

C# 计算方差
50,100,100,60,50 计算他们的方差 为了计算这些数的方差,需要进行以下步骤: 1. 计算平均值,即将这些数相加,然后除以它们的数量。 平均值 (50 100 100 60 50) / 5 72 2. 计…...

HJZS电源监视继电器HJZS-E202 AC220V
系列型号: HJZS-E202断电延时继电器 HJZS-E002断电延时继电器 一 应用 HJZS-E202电源监视继电器用于直流或交流操作的各种保护和自动控制的装置中,用以增加触点数量。 二 安装结构 导轨安装9壳体结构,具体尺寸参阅外型尺寸图。 三 产品型号…...
dolphinscheduler 2.0.6 资源中心改造方案二:通过NFS挂载共享目录
目录调度资源中心存储概要安装NFS服务器客户端调度验证关闭SFTP开关(可忽略)重新上传资源文件worker执行任务验证服务器woker客户端worker其它nfs共享目录的配置文件/etc/exports说明调度资源中心存储概要 针对现有的单机存储可以做哪些扩展?…...
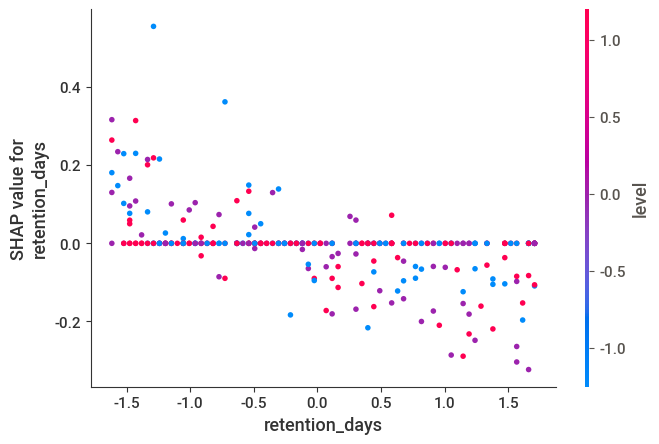
基于集成学习的用户流失预测并利用shap进行特征解释
基于集成学习的用户流失预测并利用shap进行特征解释 小P:小H,如果我只想尽可能的提高准确率,有什么好的办法吗? 小H:优化数据、调参侠、集成学习都可以啊 小P:什么是集成学习啊,听起来就很厉害的…...

【Java版oj 】 day17杨辉三角形的变形、计算某字符出现次数
目录 一、杨辉三角形的变形 (1)原题再现 (2)问题分析 (3)完整代码 二、计算某字符出现次数 (1)原题再现 (2)问题分析 (3)完整代…...

智能驾驶芯片赛道混战:如何看待5类玩家的竞争格局?
智能驾驶芯片赛道,一直是业内关注的焦点。 高工智能汽车注意到,针对L0-L2,业内基本采用智能前视一体机(IFC)方案;要实现高速NOA、城市NOA等更为高阶的智驾功能等,则基本采用域控制器方案。从IF…...

vue antd table表格的增删改查(三)input输入框根据关键字模糊查询【后台管理系统 使用filter与indexOf嵌套】
vue antd table表格的增删改查(三)input输入框根据关键字查询【后台管理系统filter与indexOf嵌套】知识回调场景复现利用filter和indexOf方法实现模糊查询1.查询对象为单层的数组元素2.查询对象为多层的数组元素(两层为例)3.查询对…...

【计组】性能指标——速度
衡量计算机性能的指标之一——速度,是指计算机执行完所有指令所耗费时间的长短。 一、概念: 引出了如下概念:机器字长:指计算机一次能处理的二进制位数,也就是我们通常说的32位64位计算机中的位。 机器字长决定了计算…...

【PC自动化测试-4】inspect.exe 详解
1,inspect.exe图解" 检查 "窗口有几个主要部分:● 标题栏。 显示" 检查 HWND (窗口句柄) 。● 菜单栏。 提供对 检查功能 的访问权限。● 工具 栏。 提供对 检查功能 的访问权限。● 树视图。 将 UI 元素的层次结构呈现为树视图控件&…...

比肩ChatGPT的国产AI:文心一言——有话说
🔗 运行环境:chatGPT,文心一言 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好&am…...

【第13届蓝桥杯】C/C++组B组省赛题目+详解
A.九进制转十进制 题目描述 九进制正整数(2022)9转换成十进制等于多少? 解: 2*9^02*9^12*9^321814581478; B.顺子日期 题目描述 小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456等。顺子日期指的就是在日期的yyyymmdd表示法中&a…...
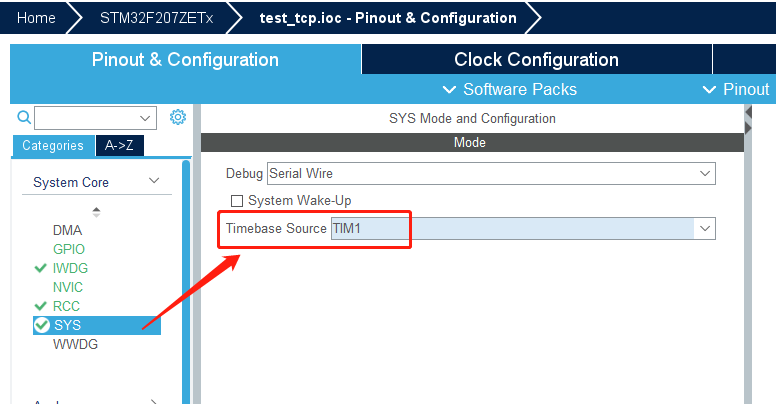
STM32 KEI 调试新手注意事项
记录一下解决问题的经过:1,用STM32 cubeMX 生成的MKD工程,默认的代码优化级别是level3 , 这个级别 会把一些代码给优化掉,造成一些意想不到的结果,最直观的就是 被优化的语句不能打断点调试,当你打了断点 ,…...

Windows权限提升—令牌窃取、UAC提权、进程注入等提权
Windows权限提升—令牌窃取、UNC提权、进程注入等提权1. 前言2. at本地命令提权2.1. 适用范围2.2. 命令使用2.3. 操作步骤2.3.1. 模拟提权2.3.2. at配合msf提权2.3.2.1. 生成木马文件2.3.2.2. 设置监听2.3.2.3. 设置反弹2.3.2.4. 查看反弹效果3. sc本地命令提权3.1. 适用范围3.…...

不做孔乙己也不做骆驼祥子
对教书育人的探讨前言一、为什么要“育人”1.育人为先2.育人是快乐的二、怎么“育人”前言 借着本次师德师风建设的主题,跟各位老师谈一谈对于“育人”的一些观点,和教育的一些看法。本文仅代表自己的观点,有不到位的地方,大家可以…...
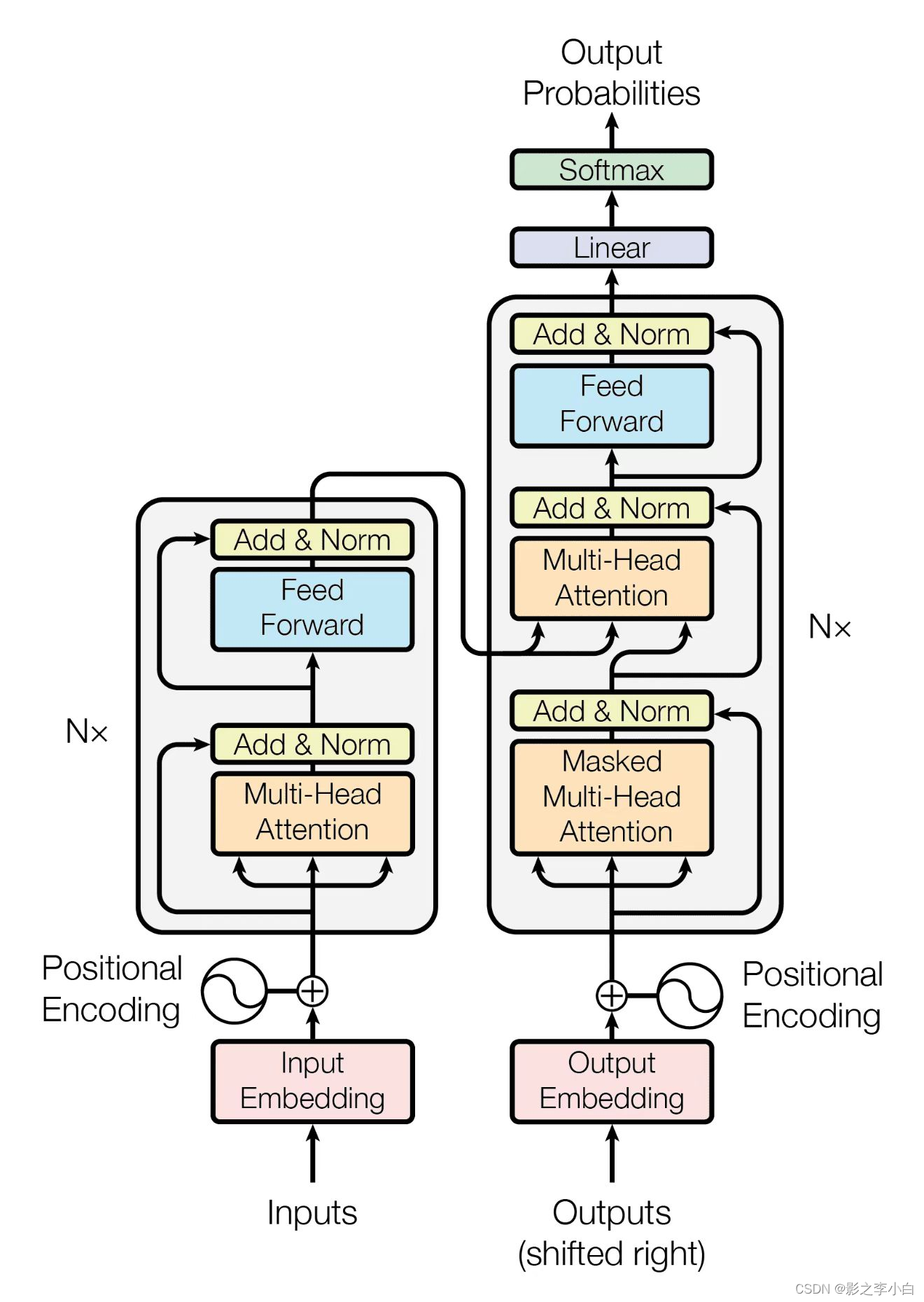
ChatGPT原理解析
文章目录Transformer模型结构构成组件整体流程GPT预训练微调模型GPT2GPT3局限性GPT4相关论文Transformer Transformer,这是一种仅依赖于注意力机制而不使用循环或卷积的简单模型,它简单而有效,并且在性能方面表现出色。 在时序模型中&#…...

常用算法实现【必会】:sort/bfs/dfs
文章目录常用排序算法实现(Go版本)BFS 广度优先遍历,利用queueDFS 深度优先遍历,利用stack前序遍历(根 左 右)中序遍历(左根右)后序遍历(左 右 根)BFS/DFS 总…...
瑟瑟发抖吧——用了这款软件,我的开发效率提升了50%
一、前言 开发中,一直听到有人讨论是否需要重复造轮子,我觉得有能力的人,轮子得造。但是往往开发周期短,用轮子所节省的时间去更好的理解业务,应用到业务中,也能清晰发现轮子的利弊,一定意义上…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...

Linux系统:进程间通信-匿名与命名管道
本节重点 匿名管道的概念与原理匿名管道的创建命名管道的概念与原理命名管道的创建两者的差异与联系命名管道实现EchoServer 一、管道 管道(Pipe)是一种进程间通信(IPC, Inter-Process Communication)机制,用于在不…...
