线性代数基础
Base
对于矩阵 A,对齐做 SVD 分解,即 U Σ V = s v d ( A ) U\Sigma V = svd(A) UΣV=svd(A). 其中 U 为 A A T AA^T AAT的特征向量,V 为 A T A A^TA ATA的特征向量。 Σ \Sigma Σ 的对角元素为降序排序的特征值。显然,U、V矩阵中的列向量相互正交,所以也可以视 V 为svd分解给出了A的列向量空间的正交基,其中最大奇异值(或特征值)对应的特征向量捕捉了数据变化的最大方向。
求满足 Ax=0 的 x
显然该问题等价于 x T A T A x = 0 x^TA^TAx = 0 xTATAx=0.
此问题有非零解 => A不满秩 => 行列式为0 => A T A A^TA ATA 的特征值至少有一个为0.
- 考虑 A A A的秩的为 k-1, 那么 A T A A^TA ATA 的特征值有一个为0。所以svd分解后V矩阵的最后一列 x ∗ x^* x∗ 就是特征值为 0 所对应的特征向量,即 A T A x ∗ = 0 ∗ x ∗ = 0 A^TA x^* = 0 * x^* = 0 ATAx∗=0∗x∗=0.
对于超定方程,极有可能不存在解析解,但存在最小二乘解满足 ∥ A x ∥ 2 \Vert Ax \Vert_2 ∥Ax∥2 最小,即最小的特征值所对应的特征向量。常见的这类问题如:已知一些三维空间中大致落在二维平面上的点,用n*3的矩阵P描述,求这个平面的法向量 n。 - 考虑 A A A的秩的为 k-2,那么那么 A T A A^TA ATA 的特征值有两个为0。
例如,已知一些落在直线上的三维点,用n*3的矩阵描述这些点,求这条线的方向n。那么显然就是求满足 m a x x ∥ A x ∥ 2 max_x \Vert Ax \Vert_2 maxx∥Ax∥2的最小二乘解,也就是最大的特征值对应的特征向量。另外,两个为0的特征值所对应的特征向量反应了在垂直直线方向的趋势,或者说向量投影到垂直直线方向(法平面)的投影。
另一个例子:存在一个bearing vector,由于bearing vector的模长固定为1,因此只能在球面上移动,其自由度为2。为了描述bearing vector的误差,所以采用bearing vector在其切平面的投影作为量化方式。那么对 bearing vectord的转置做SVD分解,则两个为0的奇异值对应的特征向量就是切平面的基。
求解Ax = b的x
此问题等价于求 A x − b = 0 Ax - b = 0 Ax−b=0。
- 当 r a n k ( A ∣ b ) = r a n k ( A ) < k rank(A|b) = rank(A) < k rank(A∣b)=rank(A)<k, 有特解+通解多个解
- 当 r a n k ( A ∣ b ) = r a n k ( A ) = k rank(A|b) = rank(A) = k rank(A∣b)=rank(A)=k, 有唯一解
- 当 r a n k ( A ∣ b ) > r a n k ( A ) rank(A|b) > rank(A) rank(A∣b)>rank(A), 无解
求解线性方程组 ( Ax = b ) 的方法有多种,具体选择取决于矩阵 ( A ) 的特性(例如,是否是方阵、是否是稀疏矩阵、是否满秩等)。以下是常见的几种方法:
1. 直接求解法
适用于方阵 ( A ) 为非奇异矩阵的情况(即 ( A ) 可逆)。
1.1 矩阵逆法
- 如果 ( A ) 是方阵且非奇异(满秩),我们可以通过矩阵的逆求解:
x = A − 1 b x = A^{-1} b x=A−1b - 优点:理论上适用于所有满秩方阵。
- 缺点:计算逆矩阵代价较高,尤其是对于大规模矩阵,数值不稳定性也可能导致精度问题。
1.2 高斯消去法
- 高斯消去法是一种通过初等行变换将 ( A ) 化为上三角矩阵,然后使用回代法求解 ( x ) 的方法。
- 步骤:
- 将 ( A ) 化为上三角矩阵(消元过程)。
- 从最后一个方程开始回代求解各个未知数。
- 优点:适合解决大部分线性方程组问题。
- 缺点:在稀疏矩阵或病态矩阵情况下可能表现不好。
1.3 LU 分解
- 将 ( A ) 分解为两个矩阵 ( L )(下三角矩阵)和 ( U )(上三角矩阵),使得 ( A = LU )。
- 分两步解决:
- 求解 ( Ly = b )(前向替换)。
- 求解 ( Ux = y )(回代)。
- 优点:可以高效地处理多次相同矩阵 ( A ) 但不同向量 ( b ) 的情况。
- 缺点:不适合奇异或病态矩阵。
2. 迭代求解法
适合大规模、稀疏矩阵,特别是在矩阵 ( A ) 具有特殊结构(例如稀疏或对称正定)的情况下。
2.1 Jacobi 方法
- 假设矩阵 ( A ) 可以分解为对角矩阵 ( D ) 和严格三角矩阵 ( L + U ),即 ( A = D + (L + U) )。
- 通过迭代更新:
x ( k + 1 ) = D − 1 ( b − ( L + U ) x ( k ) ) x^{(k+1)} = D^{-1}(b - (L+U)x^{(k)}) x(k+1)=D−1(b−(L+U)x(k)) - 优点:实现简单,适合并行计算。
- 缺点:收敛速度较慢,且不适用于所有矩阵,尤其是条件数较大的矩阵。
2.2 Gauss-Seidel 方法
- 类似于 Jacobi 方法,但在每次更新时使用新的值:
x i ( k + 1 ) = 1 A i i ( b i − ∑ j = 1 i − 1 A i j x j ( k + 1 ) − ∑ j = i + 1 n A i j x j ( k ) ) x_i^{(k+1)} = \frac{1}{A_{ii}} \left( b_i - \sum_{j=1}^{i-1} A_{ij} x_j^{(k+1)} - \sum_{j=i+1}^{n} A_{ij} x_j^{(k)} \right) xi(k+1)=Aii1(bi−j=1∑i−1Aijxj(k+1)−j=i+1∑nAijxj(k)) - 优点:比 Jacobi 方法收敛快。
- 缺点:仍可能在某些条件下收敛缓慢。
2.3 共轭梯度法
- 适用于对称正定矩阵。该方法是一种梯度下降的改进形式,通过寻找共轭方向来加速收敛。
- 步骤:
- 初始化 ( x_0 )。
- 迭代更新:
x k + 1 = x k + α k p k x_{k+1} = x_k + \alpha_k p_k xk+1=xk+αkpk
其中 ( p_k ) 是共轭方向,( \alpha_k ) 是步长。
- 优点:对大规模、稀疏、对称正定矩阵非常高效。
- 缺点:只适用于对称正定矩阵,且需要合适的预条件来保证收敛性。
3. 奇异值分解 (SVD)
适用于任意矩阵 ( A ),包括矩阵不满秩或奇异的情况。
- 奇异值分解将 ( A ) 分解为 ( A = U \Sigma V^T ),其中 ( U ) 和 ( V ) 是正交矩阵,( \Sigma ) 是对角矩阵,包含矩阵的奇异值。
- 求解过程为:
x = V Σ − 1 U T b x = V \Sigma^{-1} U^T b x=VΣ−1UTb - 优点:SVD 能处理任何矩阵,包括奇异矩阵和非方阵,是最为稳定的求解方法之一。
- 缺点:计算复杂度高,不适合大规模问题。
4. QR 分解
- QR 分解将矩阵 ( A ) 分解为正交矩阵 ( Q ) 和上三角矩阵 ( R ),即 ( A = QR )。
- 求解步骤:
- 将方程变为 ( QRx = b )。
- 左乘 ( Q^T ),得到 ( Rx = Q^T b )。
- 用回代法求解上三角矩阵 ( R ) 的方程。
- 优点:稳定性好,特别适用于不满秩的矩阵。
- 缺点:比高斯消去法稍微复杂,计算量略大。
5. 伪逆法(Moore-Penrose 逆)
适用于矩阵 ( A ) 不为方阵或不满秩的情况。
- 如果 ( A ) 是不方的或者不满秩,我们可以通过伪逆矩阵 ( A^+ ) 求解:
x = A + b x = A^+ b x=A+b
其中 ( A^+ ) 是 ( A ) 的 Moore-Penrose 伪逆。 - 优点:适用于任何矩阵(包括矩阵不满秩、奇异的情况),能找到最小范数解。
- 缺点:计算伪逆较复杂,尤其是对于大规模矩阵。
总结
- 对于方阵且 ( A ) 可逆,常用 高斯消去法 或 LU 分解。
- 对于大规模稀疏矩阵或需要迭代求解时,Jacobi 方法、Gauss-Seidel 方法 和 共轭梯度法 适用。
- 对于奇异或不满秩的矩阵,SVD 或 伪逆法 能保证稳定的解。
- QR 分解 和 高斯消去法 常用于数值稳定性要求较高的情境。
相关文章:

线性代数基础
Base 对于矩阵 A,对齐做 SVD 分解,即 U Σ V s v d ( A ) U\Sigma V svd(A) UΣVsvd(A). 其中 U 为 A A T AA^T AAT的特征向量,V 为 A T A A^TA ATA的特征向量。 Σ \Sigma Σ 的对角元素为降序排序的特征值。显然,U、V矩阵…...

LCR 021
题目:LCR 021 解法一:计算链表长度 遍历两次,第一次获取链表长度 L(包括虚拟节点),第二次遍历到第 L-n 个节点(从虚拟节点遍历) public ListNode removeNthFromEnd(ListNode head, …...

【阿雄不会写代码】全国职业院校技能大赛GZ036第四套
也不说那么多了,要用到这篇博客,肯定也知道他是干嘛的,给博主点点关注点点赞!!!这样博主才能更新更多免费的教程,不然就直接丢付费专栏里了,需要相关文件请私聊...

Vue组件:使用$emit()方法监听子组件事件
1、监听自定义事件 父组件通过使用 Prop 为子组件传递数据,但如果子组件要把数据传递回去,就需要使用自定义事件来实现。父组件可以通过 v-on 指令(简写形式“”)监听子组件实例的自定义事件,而子组件可以通过调用内建…...

数据分析-埋点
1、数据埋点的定义 针对特定用户行为或事件进行捕获、处理何发送的相关技术及其实施过程。 2、数据埋点的原理 埋点是数据采集的重要方式。通过在页面上植入代码,监控用户行为(例:页面加载、按钮点击等)。用户一旦触发了该事件,就会根据埋点信息将相关数…...

【文心智能体】通过工作流使用知识库来实现信息查询输出,一键查看旅游相关信息,让出行多一份信心
欢迎来到《小5讲堂》 这是《文心智能体平台》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 目录 创建灵感基本配置头像名称和简介人物设定角色与目标思考路…...

服务器监控工具都是监控服务器的哪些性能和指标
服务器监控工具通常用于确保服务器及其相关服务的正常运行。这些工具可以帮助管理员快速识别并解决问题,从而减少停机时间和性能下降的风险。以下是服务器监控工具通常会监控的一些主要内容: 系统健康状态: CPU使用率 内存(RAM&…...
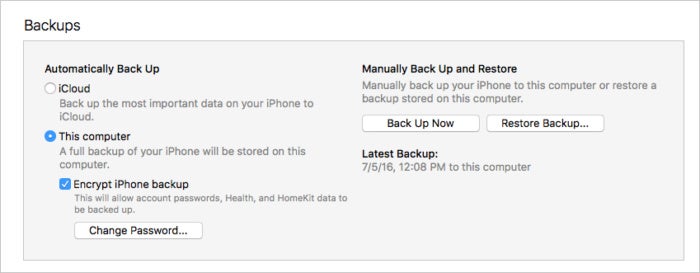
不小心删除丢失了所有短信?如何在 iPhone 上查找和恢复误删除的短信
不小心删除了一条短信,或者丢失了所有短信?希望还未破灭,下面介绍如何在 iPhone 上查找和恢复已删除的短信。 短信通常都是非正式和无关紧要的,但短信中可能包含非常重要的信息。因此,如果您删除了一些短信以清理 iPh…...

【skyvern 快速上手】一句话让AI帮你实现爬虫+自动化
目录 skyvern介绍主要特点工作流程 部署(重点介绍源码部署)源码部署docker快速部署 运行(基于源码)后端前端 快速使用示例总结 skyvern介绍 Skyvern 是一款利用大语言模型(LLM)和计算机视觉技术来自动化浏…...

【C++ Primer Plus习题】14.1
大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream> #include "wine.h" …...

在Ubuntu上运行QtCreator相关程序
背景:希望尝试在Linux系统上跑一下使用QtCreator相关的程序,因为有一些工作岗位要求有Linux上使用Qt的经验。 (1)我是把Windows上的程序移过来的,Windows上文件名称是不区分大小写的。 而Ubuntu上是区分的 所以一部分头文件需要进行修改&am…...

MybatisPlus 快速入门
目录 简介 安装 Spring Boot2 Spring Boot3 Spring 配置 Spring Boot 工程 Spring 工程 常见注解 条件构造器 流式查询 使用示例 批量操作 使用示例 自定义SQL Service接口 CRUD 扩展功能 代码生成 安装插件 通用枚举 配置枚举处理器 插件功能 配置示例…...
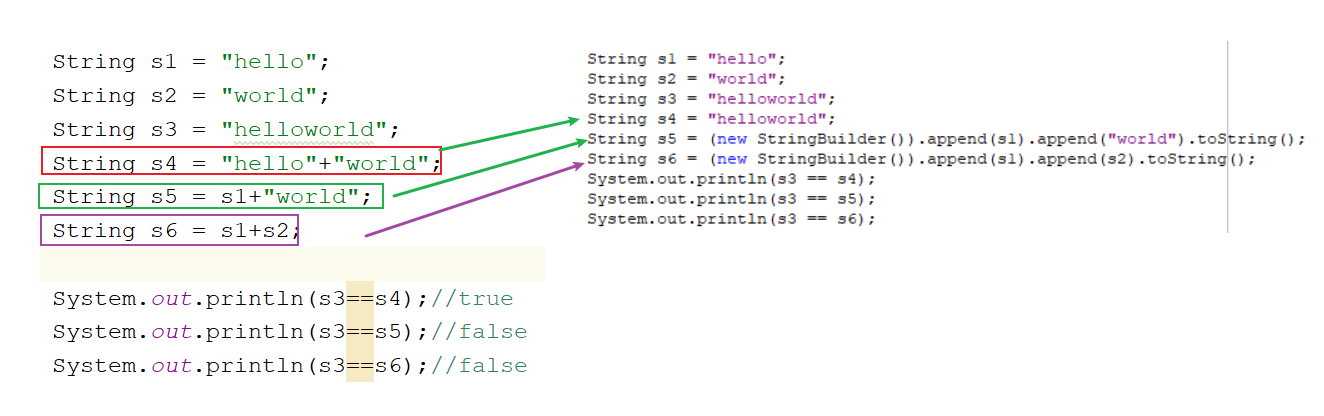
Java.lang中的String类和StringBuilder类介绍和常用方法
目录 Java.lang中的String类和StringBuilder类介绍和常用方法 String类介绍 String类的底层成员介绍 基本介绍 回顾String传址调用问题 String类对象的创建方式 String面试题 创建对象or不创建对象 创建了几个对象and共有几个对象 String常用方法 判断字符串是否相等方法 获取字…...
)
notepad++软件介绍(含安装包)
Notepad 是一款开源的文本编辑器,主要用于编程和代码编辑。它是一个功能强大的替代品,常常被用来替代 Windows 系统自带的记事本。 Notepad win系统免费下载地址 以下是 Notepad 的一些主要特点和功能: 多语言支持:Notepad 支持多…...

chapter13-常用类——(章节小结)——day17
498-常用类阶段梳理...

RTX AI PC 和工作站上部署多样化 AI 应用支持 Multi-LoRA
今天的大型语言模型(LLMs)在许多用例中都取得了前所未有的成果。然而,由于基础模型的通用性,应用程序开发者通常需要定制和调整这些模型,以便专门针对其用例开展工作。 完全微调需要大量数据和计算基础设施࿰…...

C++ STL-deque容器入门详解
1.1 deque容器基本概念 功能: 双端数组,可以对头端进行插入删除操作 deque与vector区别: vector对于头部的插入删除效率低,数据量越大,效率越低deque相对而言,对头部的插入删除速度回比vector快vector访…...

数据结构之折半查找
折半查找(Binary Search),也称为二分查找,是一种在有序数组中查找特定元素的搜索算法。其工作原理是,通过不断将待查找的区间分成两半,并判断待查找的元素可能存在于哪一半,然后继续在存在可能性…...

linux高级学习12
24.9.9学习目录 一.条件变量 一.条件变量 通常条件变量和互斥锁同时使用; 条件变量是用来阻塞线程,其本身并不是锁,直到达到特定的要求; (1)条件变量初始化 #include <pthread.h> int pthread_con…...
)
leetcode:3174 清除数字 使用栈,时间复杂度O(n)
3174 清除数字 题目链接 题目描述 给你一个字符串 s 。 你的任务是重复以下操作删除 所有 数字字符: 删除 第一个数字字符 以及它左边 最近 的 非数字 字符。 请你返回删除所有数字字符以后剩下的字符串。 示例 1: 输入:s "abc…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
