利士策分享,克服生活中的困难:走好勇攀高峰的每一步
利士策分享,克服生活中的困难:走好勇攀高峰的每一步
在这个纷繁复杂的世界里,每个人都是自己生命旅程中的行者,而生活,则是一条既铺满鲜花又布满荆棘的道路。
我们或许会在某个清晨醒来,发现自己正站在一座看似不可逾越的大山前,那就是生活中的困难。
但请记住,正是这些困难,铸就了我们坚韧不拔的品格,让我们在成长的路上更加熠熠生辉。
一、正视困难,拒绝逃避
面对困难的第一步,是勇敢地正视它,而不是选择逃避。
逃避只会让问题像滚雪球般越积越大,最终成为难以承受之重。
我们要学会像勇士一样,直面挑战,即使心中充满恐惧与不安,也要迈出那一步。
记住,每一个勇敢的开始,都是通往成功的必经之路。
二、分解目标,步步为营
当困难显得如此庞大而复杂时,不妨尝试将其分解成若干个小目标。
这样,原本看似不可完成的任务就变得具体而可行。
每完成一个小目标,都是对自己的一次肯定,也是向最终胜利迈进的一大步。
就像攀登高峰,我们需要一步步脚踏实地,才能最终站在山巅,领略那“会当凌绝顶,一览众山小”的壮阔。
三、寻求帮助,团队的力量
没有人是一座孤岛,在解决困难的过程中,我们不应孤军奋战。
家人、朋友、同事,甚至是陌生人,都可能是我们前进路上的助力。
适时地寻求帮助,不仅可以加快解决问题的速度,还能在过程中收获温暖与友谊。
记住,团队的力量是无穷的,它能让我们的路走得更远、更稳。
四、保持乐观,心态决定一切
乐观的心态是战胜困难的重要法宝。
即使前路坎坷,我们也要相信,风雨之后必有彩虹。
保持一颗积极向上的心,用笑容面对每一个挑战,你会发现,困难其实并没有想象中那么可怕。
乐观不仅能帮助我们更好地应对眼前的困境,更能激发我们内在的潜能,让我们在逆境中绽放出更加耀眼的光芒。
五、反思总结,不断成长
每一次克服困难的过程,都是一次宝贵的学习和成长经历。
在问题解决后,不妨花点时间进行反思和总结,分析自己在这场“战役”中的得与失。
这样,我们不仅能从经验中汲取教训,避免重蹈覆辙,还能在未来的道路上更加从容不迫地面对新的挑战。
六、培养韧性,逆境中的“弹簧人”
想象一下,你正站在一片荒芜的沙漠中,烈日炙烤着大地,水源几乎耗尽。
但就在这时,你发现自己体内仿佛藏着一个“弹簧”,每当跌倒,都能迅速弹起,继续前行。
这就是韧性——在逆境中不屈不挠的力量。
通过一次次的挑战与失败,你的“弹簧”越来越有弹性,让你在生活的沙漠中也能找到绿洲。
七、创新思维,点亮“脑洞”的火花
你是否曾有过这样的时刻:面对一道难题,苦思冥想却不得其解,突然灵光一闪,找到了一个前所未有的解决方案?
这就是创新思维的魅力所在。
它像一颗流星划过夜空,点亮了你的“脑洞”,让你在困境中看到了新的可能。
不妨试着从不同的角度思考问题,或者将看似不相关的事物联系起来,说不定就能激发出意想不到的创意火花。
八、自我成长的“秘密花园”
在你的内心深处,藏着一个“秘密花园”,里面种满了知识的种子、智慧的果实和情感的花朵。
当你感到疲惫或迷茫时,不妨走进这个花园,静下心来阅读一本好书、学习一项新技能或者进行一场心灵的冥想。
你会发现,随着时间的推移,这个花园会变得越来越茂盛,你的内在力量也会随之增强。
九、感恩与回馈的“温暖循环”
想象一下,你正站在一座高山的山顶,俯瞰着脚下的世界。
你心中充满了感激之情,因为你知道,没有那些在你攀登过程中给予帮助和支持的人,你就无法站在这里。
于是,你决定将自己的感激之情转化为行动,去帮助那些还在山脚下挣扎的人。
你分享自己的经验和故事,激励他们继续前行。
而你的善举又激发了更多人的感恩之心和回馈行动,形成了一个温暖的循环。
十、耐心与坚持的“时间魔法”
在时间的长河中,我们都是匆匆过客。
但正是这份短暂与珍贵,让我们更加珍惜每一个当下。
当你面对困难时,不妨想象一下时间这位魔法师正在为你施展“时间魔法”。
它让你的努力逐渐积累成河,让你的坚持在岁月的洗礼下绽放出耀眼的光芒。
记住,成功往往不是一蹴而就的,它需要时间的沉淀和积累。
只要你保持耐心、坚持不懈地努力下去,终有一天你会看到自己所付出的努力开花结果。
在人生的广阔舞台上,我们就像一群勇敢的探险家,手持名为“勇气”的火把,穿梭在名为“生活”的密林之中。
而那些不时出现的困难,就像是密林深处隐藏的巨兽,既让人心生畏惧,又激发了我们探索未知的渴望。
总之,生活中的困难就像是一场场精彩绝伦的冒险旅程。
它们让我们学会了坚韧、创新、成长、感恩和坚持。
在这个过程中,我们不断挖掘自己的潜力、拓展自己的视野、丰富自己的人生。
让我们以更加积极的心态去面对生活中的每一个挑战吧!
因为只有这样,我们才能在这场人生的冒险中留下属于自己的精彩篇章。
相关文章:

利士策分享,克服生活中的困难:走好勇攀高峰的每一步
利士策分享,克服生活中的困难:走好勇攀高峰的每一步 在这个纷繁复杂的世界里,每个人都是自己生命旅程中的行者,而生活,则是一条既铺满鲜花又布满荆棘的道路。 我们或许会在某个清晨醒来,发现自己正站在一座…...

PurchasereturnController
目录 1、 PurchasereturnController 1.1、 反审核退货单 1.1.1、 //配件ID 1.1.2、 //配件编码 1.1.3、 //修改后仓库 1.1.4、 //修改配件信息表库存量 PurchasereturnController using QXQPS.Models; using QXQPS.Vo; using System; using System.Collection…...

mysql 学习笔记 八
总结 自动提交 查看自动提交状态:SELECT AUTOCOMMIT ; 设置自动提交状态:SET AUTOCOMMIT 0 。 手动提交 AUTOCOMMIT 0 时,使用 COMMIT 命令提交事务。 事务回滚 AUTOCOMMIT 0 时,使用 ROLLBACK 命令回滚事务。 …...

反序列化漏洞练习2
拿到题目,发现目标是获得flag.php的内容,且sis中admin和passwd等于sis2407时会输出fag的内容 根据源码编写序列化代码 <?php error_reporting(0); class sis{public $admin;public $passwd;public function __construct(){$this->admin "sis2407"…...

基于SpringBoot的社区医院管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 基于JavaSpringBootVueMySQL的社团管理系统【附源码文档】、…...

YOLOv8安装配置教程(Windows版)
YOLOv8安装配置教程(Windows版) 简介:最近由于选择了人工智能方向的专业选修课,课程需要安装配置YOLOv8,经过查阅各种资料后才发现,许多教程都比较老旧,并且文件位置也发生了变化,所…...

Linux的历史,版本,Linux的环境安装、简单学习4个基本的Linux指令等的介绍
文章目录 前言一、Linux的历史二、版本三、Linux的环境安装1. 腾讯云服务器的申请2. xshell的安装与使用 四、 简单学习4个基本的Linux指令1. ls2. pwd3. mkdir4. cd 总结 前言 Linux的历史,版本,Linux的环境安装、简单学习4个基本的Linux指令等的介绍 …...

【论文阅读】01-Survey on Temporal Knowledge Graph
原文名称:Survey on Temporal Knowledge Graph 1 Introduction 目前有两种方法:基于距离模型的嵌入变换方法和基于语义匹配模型的双线性模型。它们的思想都是将包含实体和关系的知识图谱嵌入到连续的低纬度实向量空间中 时间知识图的推理有两种,第一种是…...

【AIGC】InstructPixPix:基于文本引导的图像编辑技术
github:diffusers/examples/instruct_pix2pix/train_instruct_pix2pix_sdxl.py at main huggingface/diffusers GitHub 论文:https://arxiv.org/pdf/2211.09800 摘要 我们提出了一种从人类指令编辑图像的方法:给定一个输入图像和告诉模型做什么的书面…...

无人机动力系统设计之桨叶推力计算
无人机动力系统设计之桨叶推力计算 1. 源由2. 关键参数2.1 特性参数2.1.1 材质(Material)2.1.2 叶片数量(Number of Blades)2.1.3 重量(Weight)2.1.4 噪音水平(Noise Level) 2.2 安装…...
LabVIEW重构其他语言开发的旧系统
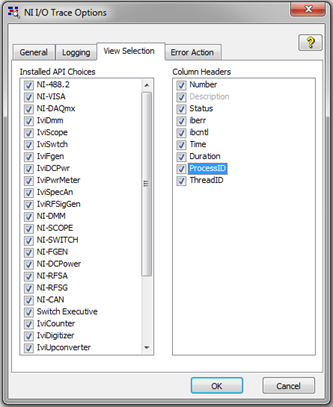
在面对一个运行已久、代码不清晰的项目时,如果该项目涉及复杂的通讯协议(如串口和488通讯),重新开发并优化成LabVIEW版本可以极大提升系统的易用性和维护性。为了确保通讯协议的顺利解析和移植,借助专业工具分析现有通…...

[晕事]今天做了件晕事43 python-byte串长度与转义字符
今天办了一件晕事,导致测试结果与预期不一致。 过程是,组装byte串的时候,整个字符串里有转义字符\x0d。 from scapy.all import IPv6, UDP pkt IPv6(src"2002:db8:a0b:12f0::157", dst"2002:db8:a0b:12f0::13")/UDP(sp…...

初识redis(String,Hash,List,Set,SortedSet)
认识NoSql sql关系型数据库 nosql非关系型数据库 nosql具有非结构化,Key/Value,Document,Draph 无关联的,非sql,BASE(原子性,持久性,一致性,隔离性) 认识r…...

Ton与ETH的一些独特的区别
文章目录 前言一、智能合约需要收取租金。二、从数据到大数据的转变三、智能合约不能运行其他合约的getter方法四、合约不是无法改变的五、Ton取消了无限制的数据结构六、钱包和地址具有独立性 前言 TON区块链是一个现代化的区块链,它为智能合约开发带来了一些全新…...

C++ | Leetcode C++题解之第396题旋转图像
题目: 题解: class Solution { public:int maxRotateFunction(vector<int>& nums) {int f 0, n nums.size();int numSum accumulate(nums.begin(), nums.end(), 0);for (int i 0; i < n; i) {f i * nums[i];}int res f;for (int i …...

前向渲染路径
1、前向渲染路径处理光照的方式 前向渲染路径中会将光源分为以下3种处理方式: 逐像素处理(需要高等质量处理的光)逐顶点处理(需要中等质量处理的光)球谐函数(SH)处理(需要低等质量…...

Python画笔案例-040 绘制五角星顶圆
1、绘制五角星顶圆 通过 python 的turtle 库绘制五角星顶圆,如下图: 2、实现代码 绘制五角星顶圆,以下为实现代码: """五角星顶圆.py """ import turtledef draw_circle(d):turtle.left(90)for _ …...

【区块链 + 人才服务】可信教育区块链治理系统 | FISCO BCOS应用案例
伴随着区块链技术的不断完善,其在教育信息化中的应用也在持续发展。利用区块链数据共识、不可篡改的特性, 将与教育相关的数据要素在区块链上进行存证确权,在确保数据可信的前提下,促进教育的公平、透明、开放,为教育教…...
)
期货量化-群体优化算法:混合蛙跳算法(SFL)
1. 概述 混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFL)由 M. Eusuff 等人在2003年提出。这一算法结合了模因算法与粒子群优化算法的原理,灵感来源于一群青蛙在觅食过程中的行为模式。 SFL 最初作为一种求解组合优化问题的元启发式方法…...

tensorflow-线性回归python入门
目录 读入库 构造数据 建立训练和测试数据 创建第一层到最后一层的神经网络 开始测试 sin函数回归 读入库 import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import time 构造数据 X np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
