电子技术——共模抑制
电子技术——共模抑制

我们在之前学习过,无论是MOS还是BJT的差分输入对,共模信号并不会改变漏极电流的大小,因此我们说差分输入对共模信号无响应。但是实际上由于各种客观非理想因素,例如电流源有限阻抗等,此时共模是影响差分输入对的。
MOS的情况
RSSR_{SS}RSS 的影响
下图是一个MOS的差分输入对,但是电流源是有限阻抗的,阻抗大小为 RSSR_{SS}RSS ,而且我们输入端有两个电压,一是信号本身固有的共模电压 VCMV_{CM}VCM ,另外一个是外界干扰的共模电压 vicmv_{icm}vicm 可能是干扰信号,也可能是噪波。我们的目的就是讨论 vicmv_{icm}vicm 对输出电压的影响:
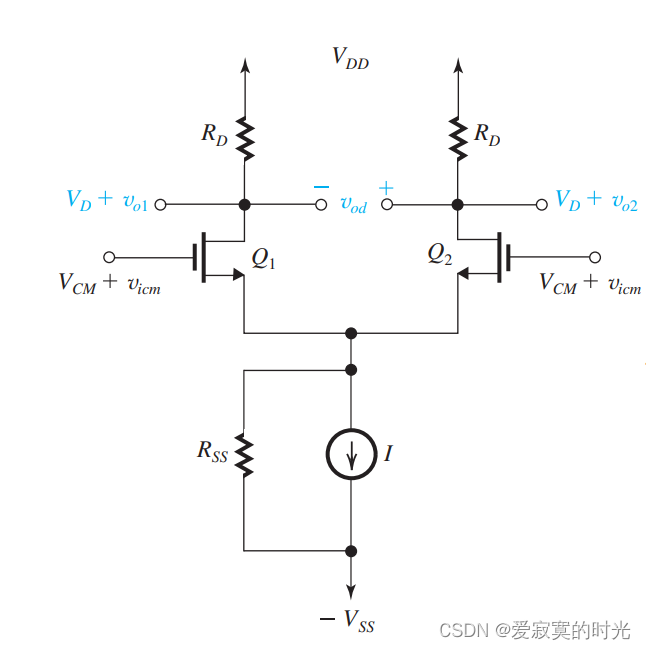
首先我们讨论一下 RSSR_{SS}RSS 对偏置的影响,由于 RSSR_{SS}RSS 的存在,流过MOS的电流要比 I/2I/2I/2 稍稍大一些。然而一般情况下 RSSR_{SS}RSS 都是非常巨大的,因此超出 I/2I/2I/2 的那一部分几乎可以忽略。其次 RSSR_{SS}RSS 对 AdA_dAd 也是没有影响的,这是因为假设MOS都是完全相同的,此时源极永远都是虚拟地, RSSR_{SS}RSS 无影响。
现在我们讨论 vicmv_{icm}vicm 存在的影响,考虑下面的电路:
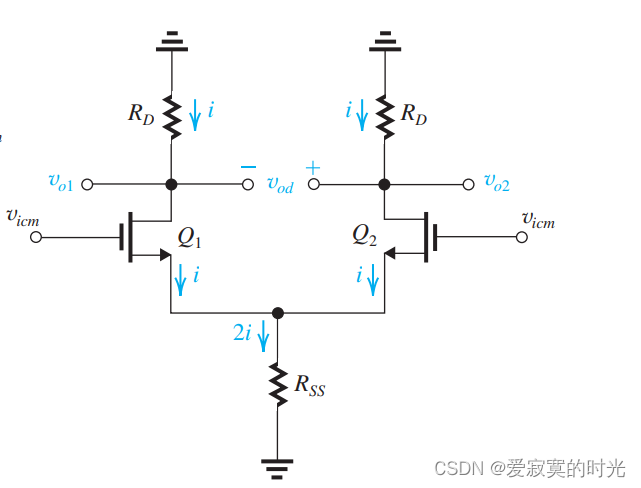
我们移除了所有的DC分量,只考虑信号作用,此时电路仍然是完全对称的,我们将MOS的漏极信号电流记为 iii 则流过 RSSR_{SS}RSS 的电流为 2i2i2i 。我们使用等效T模型分析:
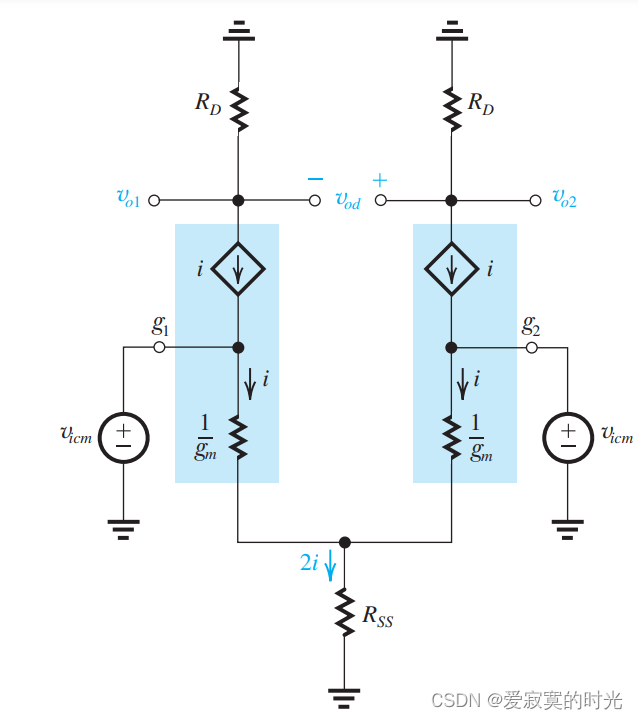
则有:
vicm=igm+2iRSSv_{icm} = \frac{i}{g_m} + 2iR_{SS} vicm=gmi+2iRSS
所以:
i=vicm1/gm+2RSSi = \frac{v_{icm}}{1/g_m + 2R_{SS}} i=1/gm+2RSSvicm
输出信号电压为:
vo1=vo2=−RD1/gm+2RSSvicmv_{o1} = v_{o2} = -\frac{R_D}{1/g_m + 2R_{SS}}v_{icm} vo1=vo2=−1/gm+2RSSRDvicm
这就说明 vo1v_{o1}vo1 和 vo2v_{o2}vo2 是受 vicmv_{icm}vicm 影响的,影响的比例大约为:
vovicm≃−RD2RSS\frac{v_o}{v_{icm}} \simeq -\frac{R_D}{2R_{SS}} vicmvo≃−2RSSRD
这里我们假设 2RSS≫1/gm2R_{SS} \gg 1/g_m2RSS≫1/gm ,尽管如此,其差分输出信号仍然为零。
vod=vo2−vo1=0v_{od} = v_{o2} - v_{o1} = 0 vod=vo2−vo1=0
MOS差分输入对抑制了全部的共模信号,是我们想要的结果。但是事实上并不总是如此,特别是电路不对称的情况。由于现在电路的对称性,我们仍然可以使用半电路分析:
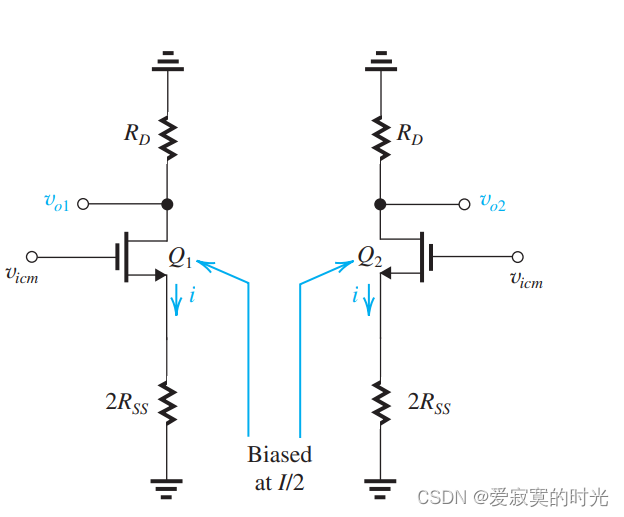
这种半电路我们称为 共模半电路 。
RDR_DRD 不匹配的影响
另一种非理想因素是 RDR_DRD 不匹配,我们假设 Q1Q_1Q1 为 RDR_DRD 而 Q2Q_2Q2 为 RD+ΔRDR_D + \Delta R_DRD+ΔRD ,此时的输出端信号电流为:
vo1≃−RD2RSSvicmv_{o1} \simeq -\frac{R_D}{2R_{SS}} v_{icm} vo1≃−2RSSRDvicm
vo2≃−RD+ΔRD2RSSvicmv_{o2} \simeq -\frac{R_D + \Delta R_D}{2R_{SS}} v_{icm} vo2≃−2RSSRD+ΔRDvicm
所以差分信号电压为:
vod=vo2−vo1=−ΔRD2RSSvicmv_{od} = v_{o2} - v_{o1} = -\frac{\Delta R_D}{2R_{SS}}v_{icm} vod=vo2−vo1=−2RSSΔRDvicm
我们记其 共模增益 为:
Acm≡vodvicm=−ΔRD2RSSA_{cm} \equiv \frac{v_{od}}{v_{icm}} = -\frac{\Delta R_D}{2R_{SS}} Acm≡vicmvod=−2RSSΔRD
还可以表示为:
Acm=−(RD2RSS)(ΔRDRD)A_{cm} = -(\frac{R_D}{2R_{SS}})(\frac{\Delta R_D}{R_D}) Acm=−(2RSSRD)(RDΔRD)
这说明 RDR_DRD 不匹配会影响 vodv_{od}vod 的输出,即 vodv_{od}vod 存在 vicmv_{icm}vicm 分量,这个分量是我们不想要的。为了衡量 vicmv_{icm}vicm 的占比,我们引入 共模抑制比 定义为:
CMRR≡∣Ad∣∣Acm∣CMRR \equiv \frac{|A_d|}{|A_{cm}|} CMRR≡∣Acm∣∣Ad∣
经常使用分贝来表示:
CMRR(dB)=20log∣Ad∣∣Acm∣CMRR(dB) = 20 \log{\frac{|A_d|}{|A_{cm}|}} CMRR(dB)=20log∣Acm∣∣Ad∣
RDR_DRD 不匹配带来的共模抑制比为:
CMRR=(2gmRSS)/(ΔRDRD)CMRR = (2g_mR_{SS}) / (\frac{\Delta R_D}{R_D}) CMRR=(2gmRSS)/(RDΔRD)
为了获得更大的共模抑制比,我们可以增大偏置电流,或者增大电流源输出阻抗,以及尽可能使得电路匹配,即 (ΔRDRD)(\frac{\Delta R_D}{R_D})(RDΔRD) 尽量小。
gmg_mgm 不匹配的影响
另外一种非理想因素是两个MOS管本身不匹配,可以看做是 gmg_mgm 不匹配的影响。我们假设:
gm1=gm+12Δgmg_{m1} = g_m + \frac{1}{2}\Delta g_m gm1=gm+21Δgm
gm2=gm−12Δgmg_{m2} = g_m - \frac{1}{2}\Delta g_m gm2=gm−21Δgm
也就是:
gm1−gm2=Δgmg_{m1} - g_{m2} = \Delta g_m gm1−gm2=Δgm
虽然此时电路不对称,我们无法使用半电路法分析,我们可以使用直接计算得到:
Acm≃(RD2RSS)(Δgmgm)A_{cm} \simeq (\frac{R_D}{2R_{SS}})(\frac{\Delta g_m}{g_m}) Acm≃(2RSSRD)(gmΔgm)
则共模抑制比为:
CMRR=(2gmRSS)/(Δgmgm)CMRR = (2g_mR_{SS}) / (\frac{\Delta g_m}{g_m}) CMRR=(2gmRSS)/(gmΔgm)
这个形式和 RDR_DRD 不匹配的影响一样。同样的为了获得更大的共模抑制比,我们可以增大偏置电流,或者增大电流源输出阻抗,以及尽可能使得电路匹配,即 (Δgmgm)(\frac{\Delta g_m}{g_m})(gmΔgm) 尽量小。
差分输出和单端输出
以上的讨论都是基于差分输出而言的,如果使用的是单端输出,则CMRR会大大降低,这是因为在本节一开始我们就分析了,即使如果电路是对称的,那么 vicmv_{icm}vicm 也会出现在输出端的两端,如果使用单端输出 vicmv_{icm}vicm 就会出现在输出电压上。如果我们想获得较大的CMRR,我们推荐使用差分输出。之后我们会介绍如何保持CMRR无损的将差分信号转换为单端信号。
BJT的情况
同样对于BJT也存在共模抑制的情况,我们使用如下图的电路以及对应的半电路:
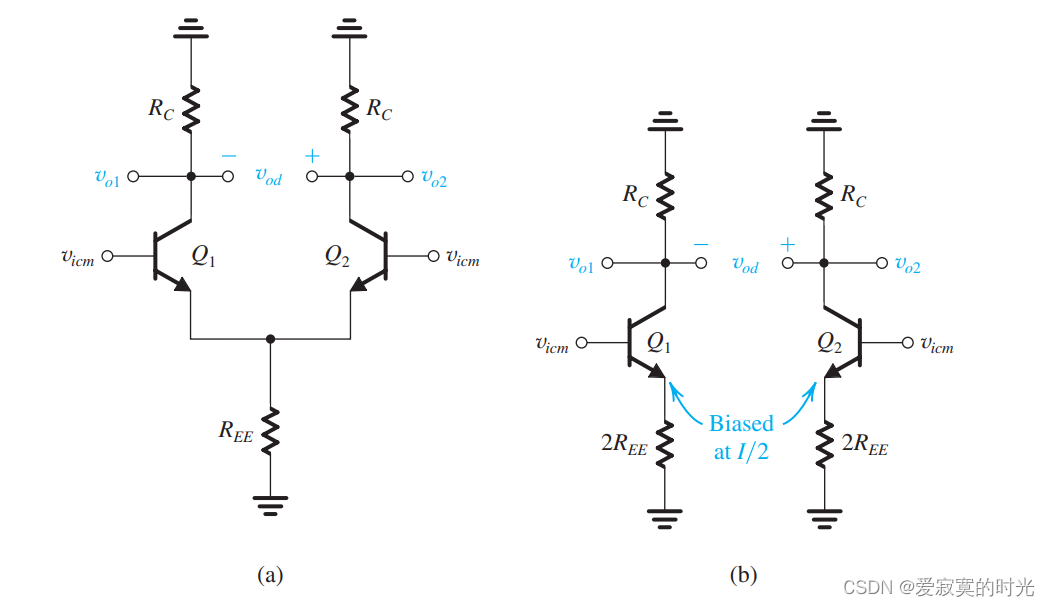
输出信号电压为:
vo1=vo2=−αRCre+2REEvicmv_{o1} = v_{o2} = -\frac{\alpha R_C}{r_e + 2R_{EE}}v_{icm} vo1=vo2=−re+2REEαRCvicm
说明BJT的同样抑制共模信号。但是当出现电路不匹配的情况下,例如存在 ΔRC\Delta R_CΔRC :
Acm=−αΔRC2REE+reA_{cm} = -\frac{\alpha \Delta R_C}{2R_{EE} + r_e} Acm=−2REE+reαΔRC
因为 α≃1,re≪2REE\alpha \simeq 1,r_e \ll 2R_{EE}α≃1,re≪2REE 所以:
Acm≃−(RC2REE)(ΔRCRC)A_{cm} \simeq - (\frac{R_C}{2R_{EE}})(\frac{\Delta R_C}{R_C}) Acm≃−(2REERC)(RCΔRC)
因此共模抑制比为:
CMRR=(2gmREE)/(ΔRCRC)CMRR = (2g_m R_{EE}) / (\frac{\Delta R_C}{R_C}) CMRR=(2gmREE)/(RCΔRC)
与MOS具有相同的形式。
BJT的输入阻抗是有限的,因此对于 vicmv_{icm}vicm 来说也存在输入阻抗,如图:
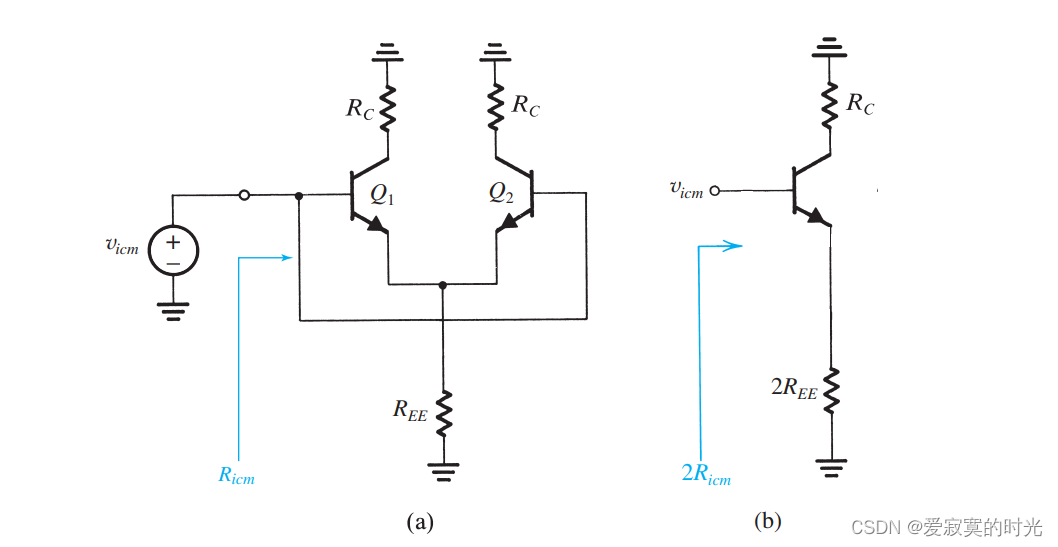
我们定义 RicmR_{icm}Ricm 是共模信号的输入阻抗,对应的等效半电路输入阻抗为 2Ricm2R_{icm}2Ricm 我们有:
Ricm≃βREE1+RC/βro1+RC+2REEroR_{icm} \simeq \beta R_{EE} \frac{1 + R_C / \beta r_o}{1 + \frac{R_C + 2R_{EE}}{r_o}} Ricm≃βREE1+roRC+2REE1+RC/βro
相关文章:

电子技术——共模抑制
电子技术——共模抑制 我们在之前学习过,无论是MOS还是BJT的差分输入对,共模信号并不会改变漏极电流的大小,因此我们说差分输入对共模信号无响应。但是实际上由于各种客观非理想因素,例如电流源有限阻抗等,此时共模是影…...

对KMP简单的理解
声明:下边的例子均表示下标从1开始的数组 ne数组的定义: next[i] 就是使子串 s[1…i] 有最长相等前后缀的前缀的最后一位的下标。ne[i]也可以表示相等子串的长度 准备执行jne[j]时, 表示当前s[i]!p[j1] , 如果ne[j]1 ,那么下…...

Hibernate不是过时了么?SpringDataJpa又是什么?和Mybatis有什么区别?
一、前言 ps: 大三下学期,拿到了一份实习。进入公司后发现用到的技术栈有Spring Data Jpa\Hibernate,但对于持久层框架我只接触了Mybatis\Mybatis-Plus,所以就来学习一下Spring Data Jpa。 1.回顾MyBatis 来自官方文档的介绍:MyBatis 是一款…...
数学建模拓展内容:卡方检验和Fisher精确性检验(附有SPSS使用步骤)
卡方检验和Fisher精确性检验卡方拟合度检验卡方独立性检验卡方检验的前提假设Fisher精确性检验卡方拟合度检验 卡方拟合度检验概要:卡方拟合度检验也被称为单因素卡方检验,用于检验一个分类变量的预期频率和观察到的频率之间是否存在显著差异。 卡方拟…...

【Python学习笔记之七大数据类型】
Python数据类型:Number数字、Boolean布尔值、String字符串、list列表、tuple元组、set集合、dictionary字典 int整数 a1 print(a,type(a))float浮点数 b1.1 print(b,type(b))complex复数 c100.5j print(c,type(c))bool布尔值:True、False,true和false并非Python…...

Android系统之onFirstRef自动调用原理
前言:抽丝剥茧探究onFirstRef究竟为何在初始化sp<xxx>第一个调用?1.onFirstRef调用位置<1>.system/core/libutils/RefBase.cpp#include <utils/RefBase.h>//1.初始化强指针 void RefBase::incStrong(const void* id) const {weakref_i…...
ipv6上网配置
一般现在的宽带都已经支持ipv6了,但是需要一些配置才能真正用上ipv6。记录一下配置过程。 当前测试环境为移动宽带,光猫下面接了一个路由器,家里所有的设备都挂到这个路由器下面的。 1. 光猫改桥接 光猫在使用路由模式下,ipv6无…...

python实现聚类技术—复杂网络社团检测 附完整代码
实验内容 某跆拳道俱乐部数据由 34 个节点组成,由于管理上的分歧,俱乐部要分解成两个社团。 该实验的任务即:要求我们在给定的复杂网络上检测出两个社团。 分析与设计 实验思路分析如下: 聚类算法通常可以描述为用相似度来衡量两个数据的远近,搜索可能的划分方案,使得目标…...
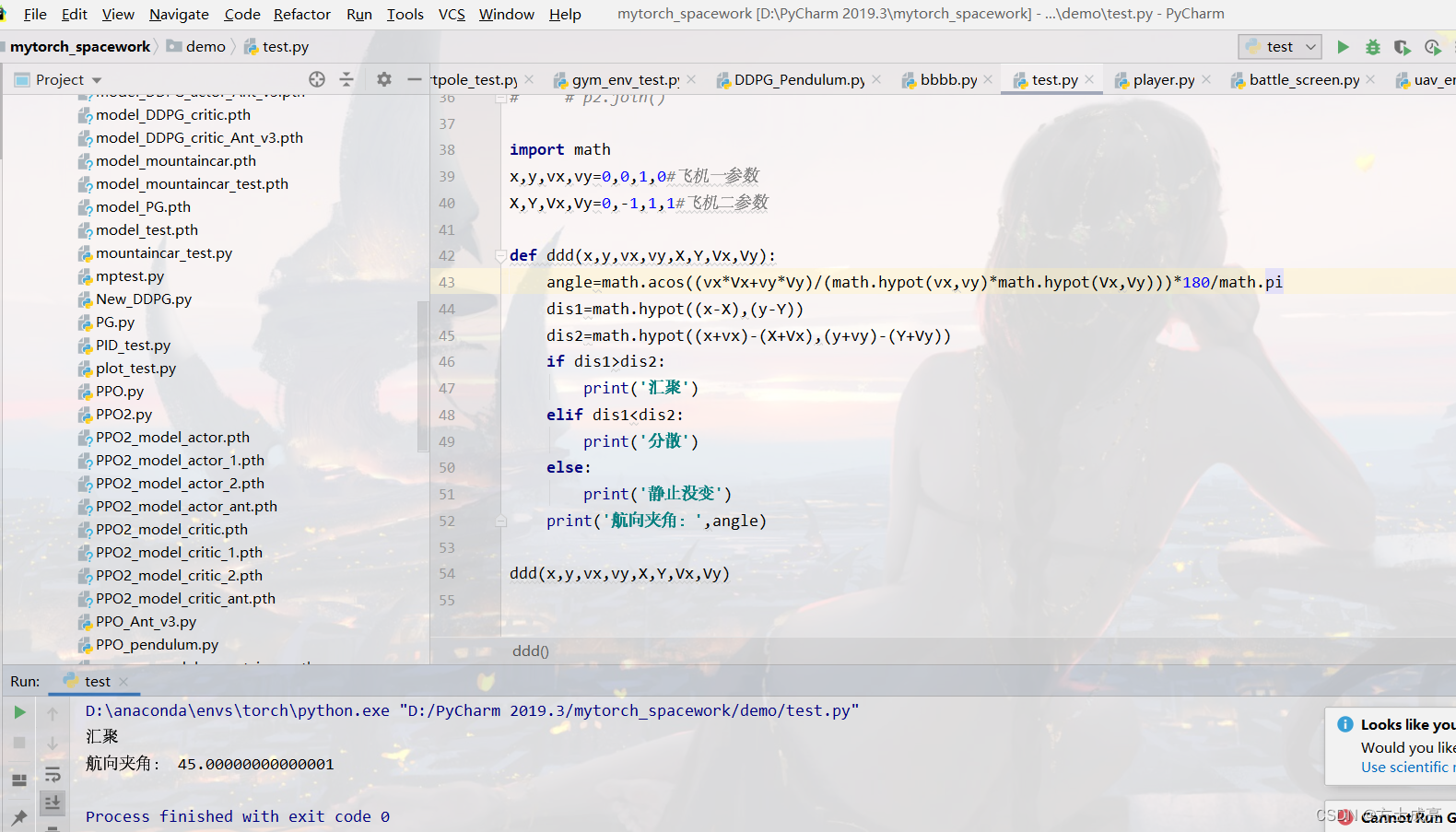
如何判断两架飞机在汇聚飞行?(如何计算两架飞机的航向夹角?)内含程序源码
ok,在开始一切之前,让我先猜一猜,你是不是想百度“二维平面下如何计算两个移动物体的航向夹角?”如果是,那就请继续往下看。 首先,我们要明确一个概念:航向角≠航向夹角!࿰…...

Scipy稀疏矩阵bsr_array
文章目录基本原理初始化内置方法基本原理 bsr,即Block Sparse Row,bsr_array即块稀疏行矩阵,顾名思义就是将稀疏矩阵分割成一个个非0的子块,然后对这些子块进行存储。通过输入维度,可以创建一个空的bsr数组࿰…...

LeetCode笔记:Weekly Contest 332
LeetCode笔记:Weekly Contest 332 1. 题目一 1. 解题思路2. 代码实现 2. 题目二 1. 解题思路2. 代码实现 3. 题目三 1. 解题思路2. 代码实现 4. 题目四 1. 解题思路2. 代码实现 比赛链接:https://leetcode.com/contest/weekly-contest-332/ 1. 题目一…...

autox.js在vscode(win7)与雷神模拟器上的开发环境配置
目录 下载autox.js 安装autox.js? 在电脑上搭建autox.js开发环境 安装vscode 安装autox.js插件 雷神模拟器连接vscode 设置雷神模拟器IP 设置autox.js应用IP地址等 下载autox.js 大体来说,就是一个运行在Android平台上的JavaScript 运行环境 和…...

创建阿里云物联网平台
创建阿里云物联网平台 对云平台设备创建过程做记录,懒得再看视频 文章参考视频:https://www.bilibili.com/video/BV1jP4y1E7TJ?p26&vd_source50694678ae937a743c59db6b5ff46c31 阿里云:https://www.aliyun.com 1.物联网平…...
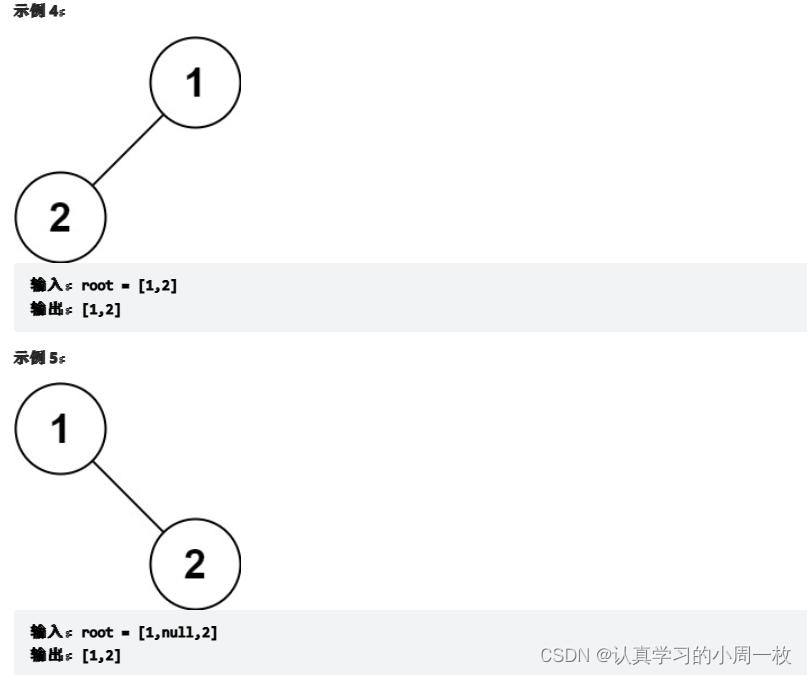
【链式二叉树】数据结构链式二叉树的(万字详解)
前言: 在上一篇博客中,我们已经详解学习了堆的基本知识,今天带大家进入的是二叉树的另外一种存储方式----“链式二叉树”的学习,主要用到的就是“递归思想”!! 本文目录1.链式二叉树的实现1.1前置说明1.2结…...

Koa2篇-简单介绍及使用
一.简介koa2是基于 Node.js 平台的下一代 web 开发框架, 致力于成为一个更小、更富有表现力、更健壮的 Web 框架。 可以避免异步嵌套. express中间件是异步回调,Koa2原生支持async/await二.async/awaitconst { rejects } require("assert"); const { resolve } req…...
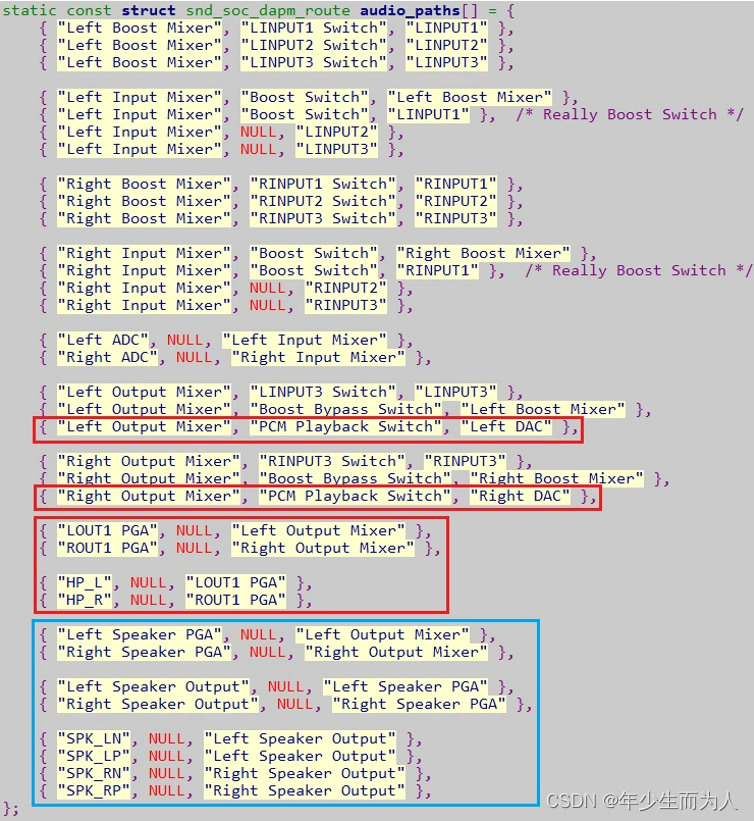
Linux ALSA 之十一:ALSA ASOC Path 完整路径追踪
ALSA ASOC Path 完整路径追踪一、ASoc Path 简介二、ASoc Path 完整路径2.1 tinymix 设置2.2 完整路径 route一、ASoc Path 简介 如前面小节所描述,ASoc 中 Machine Driver 是 platform driver 和 codec driver 的粘合剂,audio path 离不开 FE/BE/DAI l…...

【Spring Cloud总结】1、服务提供者与服务消费者快速上手
目录 文件结构 代码 1、api 1.1实体类(Dept ) 1.2数据库 2、provider 2.1 DeptController 2.2 DeptDao 2.3 DeptService 2.4 DeptServiceImpl 2.5 application.yml 3、consumer 3.1 ConfigBean 3.2 DeptConsumerController 测试 1.启动…...

若依项目学习之登录生成验证码
若依项目学习之登录生成验证码 使用DefaultKaptcha生成验证码 /*** 验证码配置* * author ruoyi*/ Configuration public class CaptchaConfig {/*** 生成字符类型的验证码**/Bean(name "captchaProducer")public DefaultKaptcha getKaptchaBean(){DefaultKaptcha…...
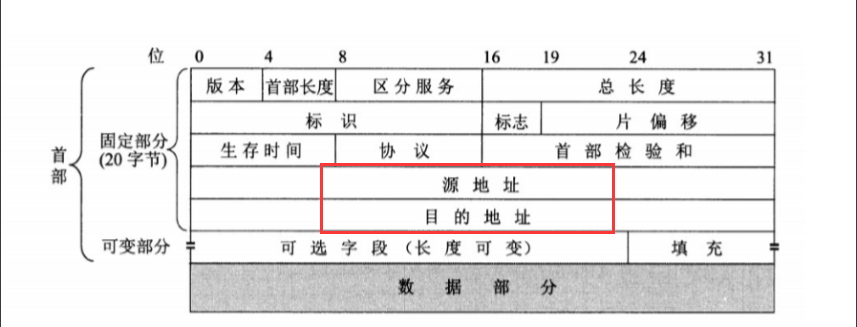
计算机网络5:数据在两台计算机之间是怎样传输的?
数据在两台计算机之间的传输总的来说包括了封装和解封两个过程 封装(5层协议) 以传送一张图片为例 **应用层:**将jpg格式的图片数据转化成计算机可以识别的0101的二进制的比特流 **传输层:**将应用层传输下来的数据进行分段&…...

就现在!为元宇宙和Web3对互联网的改造做准备!
欢迎来到Hubbleverse 🌍 关注我们 关注宇宙新鲜事 📌 预计阅读时长:8分钟 本文仅代表作者个人观点,不代表平台意见,不构成投资建议。 如今,互联网是各种不同的网站、应用程序和平台的集合。由于彼此分离…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
