OFDM信号PARP的CCDF图
文章目录
- 引言
- 代码
- 代码疑难解答
- 参考文献
引言
本书主要参考了文献1,但实际上该书中符号和表述的错误非常多(只能说棒子是这样的);同时因为发表时间的关系,很多MATLAB代码进行了更新,原书提供的代码已经无法正常运行。我将修补后的代码给出,并且给出了疑难问题的理解。
代码
% plot_CCDF.m
% Plot the CCDF curves of Fig. 7.3.clear all; clc; clf
N_OFDM = 2.^[6:10]; %N_OFDM代表OFDM中做IFFT点的数量
b=2; M=2^b;
Nblk = 1e4; % Nblk Number of Blocks
PARP_dB = [4:0.1:10];
N_PARP_dB = length(PARP_dB);CCDF_formula=inline('1-((1-exp(-z.^2/(2*s2))).^N)','N','s2','z'); % Eq.(7.9) 构造一个内联函数对象for n = 1:length(N_OFDM) N=N_OFDM(n); x = zeros(Nblk,N); sqN=sqrt(N);for k = 1:NblkX = mapper(b,N); % 生成 N 个 2^b QAM modulated symbols x(k,:) = ifft(X,N)*sqN; % 确保IFFT变换后能量一致CFx(k) = PAPR(x(k,:)); % 计算信号的PAPRend% 通过锐利信道特性计算平均的σ^2的值sigma2 = mean(mean(abs(x)))^2/(pi/2);% 计算CCDF的理论值 the maximum of Zn is equivalent to the crest factor, sqrt(PAPR)CCDF_theoretical=CCDF_formula(N,sigma2,10.^(PARP_dB/20)); for i = 1:N_PARP_dBCCDF_simulated(i) = sum(CFx>PARP_dB(i))/Nblk;end% 绘制对数图semilogy(PARP_dB,CCDF_theoretical,'k-'); hold on; grid on;semilogy(PARP_dB(1:3:end),CCDF_simulated(1:3:end),'k:*');
endaxis([PARP_dB([1 end]) 1e-2 1]); % 确认坐标轴范围
title('OFDM system with N-point FFT');
xlabel('PAPR0[dB]'); ylabel('CCDF=Probability(PAPR>PAPR0)');
legend('Theoretical','Simulated');
function [modulated_symbols,Mod] = mapper(b,N)
% If N is given, it generates a block of N random 2^b-PSK/QAM modulated symbols.
% Otherwise, it generates a block of 2^b-PSK/QAM modulated symbols for [0:2^b-1].M=2^b; % Modulation order or Alphabet (Symbol) size% 生成一个相移键控 PSK 调制器对象
if b==1, Mod='BPSK'; A=1; mod_object=comm.PSKModulator('ModulationOrder', M);
elseif b==2, Mod='QPSK'; A=1;%QPSK 调制的信号星座图是一个单位圆的 4 个点,表示 0 度、90 度、180 度和 270 度的相位mod_object=comm.PSKModulator('ModulationOrder', M,'PhaseOffset',pi/4);
else% 生成一个 QAM 调制器对象Mod=[num2str(2^b) 'QAM']; Es=1; A=sqrt(3/2/(M-1)*Es);mod_object=comm.RectangularQAMModulator('ModulationOrder', M, 'SymbolMapping', 'Gray');
end% 虽然这里是用了A来做功率归一化,实际上调制器函数本身就自带有归一化功能
if nargin==2 % generates a block of N random 2^b-PSK/QAM modulated symbolsmodulated_symbols = A*mod_object(randi([0 M-1], N, 1));
elsemodulated_symbols = A*mod_object([0:M-1]');
end
function [PAPR_dB, AvgP_dB, PeakP_dB] = PAPR(x)
% PAPR_dB : PAPR[dB]
% AvgP_dB : Average power[dB]
% PeakP_dB : Maximum power[dB]%MIMO-OFDM Wireless Communications with MATLAB㈢ Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte LtdNx=length(x); xI=real(x); xQ=imag(x);
Power = xI.*xI + xQ.*xQ;
PeakP = max(Power); PeakP_dB = 10*log10(PeakP);
AvgP = sum(Power)/Nx; AvgP_dB = 10*log10(AvgP);
PAPR_dB = 10*log10(PeakP/AvgP);
代码疑难解答
- 为什么要使用
x(k,:) = ifft(X,N)*sqN;这个IFFT公式
这是为了是变换前后时域和频率域的能量保持一致。
- σ 2 \sigma^2 σ2 这个式子是如何计算,这个计算是必须的吗?
根据锐利分布的公式,平均值 E ( X ) = σ π / 2 E(X)=\sigma\sqrt{\pi/2} E(X)=σπ/2。详细推导可以参考概率分布的教科书。但实际上, σ 2 \sigma^2 σ2 根据默认的设置应该是 σ 2 = 0.5 \sigma^2=0.5 σ2=0.5。因为我们对输入功率在
mapper函数中就进行了归一化处理。sigma2 = mean(mean(abs(x)))^2/(pi/2);这一行代码实际上是没有必要的。下图是设置 σ 2 = 0.5 \sigma^2=0.5 σ2=0.5 后仿真结果图。
- 为什么横坐标要改成PARP0[dB],而不是原本的z[dB]?
实际上,这主要取决于代码。原书本中的图是明显错误的。
参考文献
- MIMO-OFDM无线通信技术及MATLAB实现
- 初识OFDM(八):OFDM中的PAPR计算和通频带仿真
相关文章:

OFDM信号PARP的CCDF图
文章目录 引言代码代码疑难解答参考文献 引言 本书主要参考了文献1,但实际上该书中符号和表述的错误非常多(只能说棒子是这样的);同时因为发表时间的关系,很多MATLAB代码进行了更新,原书提供的代码已经无法…...

LeetCode之高频SQL50题
查询 1757. 可回收且低脂的产品 584. 寻找用户推荐人 595. 大的国家 1148. 文章浏览 I 1683. 无效的推文 连接 1378. 使用唯一标识码替换员工ID 1068. 产品销售分析 I 1581. 进店却未进行过交易的顾客 197. 上升的温度 1661. 每台机器的进程平均运行时间 577. 员工…...

echarts多组堆叠柱状图
一、效果图 二、代码实现 1、创建容器 <el-card class"box-card"><div slot"header" class"clearfix"><span>课堂学习</span></div><div id"class-learning" style"height: 360px">&l…...
打造安心宠物乐园:EasyCVR平台赋能猫咖/宠物店的智能视频监控解决方案
随着宠物经济的蓬勃发展,宠物店与猫咖等场所对顾客体验、宠物安全及健康管理的需求日益提升。然而,如何确保这些场所的安全与秩序,同时提升顾客体验,成为了经营者们关注的焦点。引入高效、智能的视频监控方案,不仅能够…...
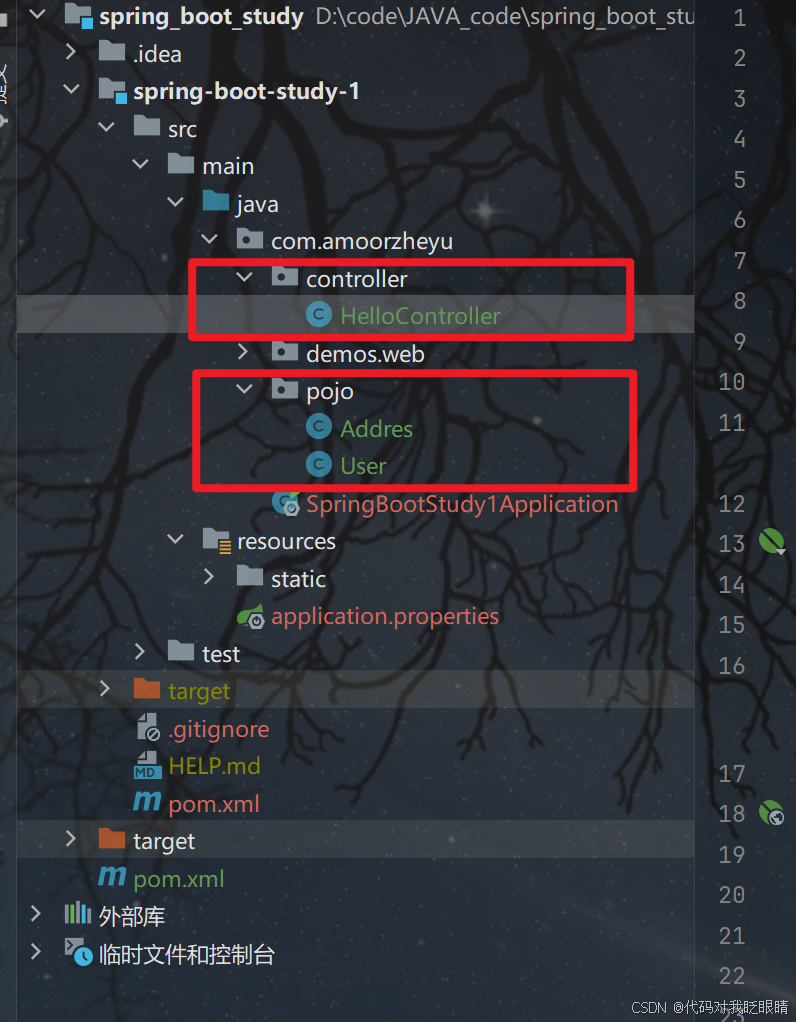
springboot请求传参常用模板
注释很详细,直接上代码 项目结构 源码 HelloController package com.amoorzheyu.controller;import com.amoorzheyu.pojo.User; import org.springframework.format.annotation.DateTimeFormat; import org.springframework.web.bind.annotation.*;import java.ti…...
HTML/CSS/JS学习笔记 Day4(HTML--C3 表格)
跟着该视频学习,记录笔记:【黑马程序员pink老师前端入门教程,零基础必看的h5(html5)css3移动端前端视频教程】https://www.bilibili.com/video/BV14J4114768?p12&vd_source04ee94ad3f2168d7d5252c857a2bf358 Day4 内容梳理:…...

WPF中创建横向的ListView
在WPF中,要创建横向的ListView,您可以通过设置ItemsControl的ItemsPanel来改变其项的排列方向。以下是一个简单的示例,展示了如何将ListView的项横向排列: 在这个例子中,WrapPanel用于横向排列其子元素,而…...

A表和B表公共元素产生链表C
设A和B是两个单链表(带头节点),其中元素递增有序。设计一个算法从A到B的公共元素产的C表(交集),要求不破坏A,B的节点。 思想:依次比较A,B表中的元素,相同时&…...

Rust运算符
【图书介绍】《Rust编程与项目实战》-CSDN博客 《Rust编程与项目实战》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 (jd.com) https://blog.csdn.net/brucexia/category_12779443.html 前面已经学习了变量和常量,本节开始对它们进行操作,…...

Oracle rman 没有0级时1级备份和0级大小一样,可以用来做恢复 resetlogs后也可以
文档说了 full backup 不能 用于后续的level 1,没说level 1没有level 0 是不是level 1就是level 0? 1级备份变0级的原因 及 Enabling Change Tracking生效没有-CSDN博客 这个文档说明1级备份时没有找到0级就是0级备份,可以用来完整恢复的。…...
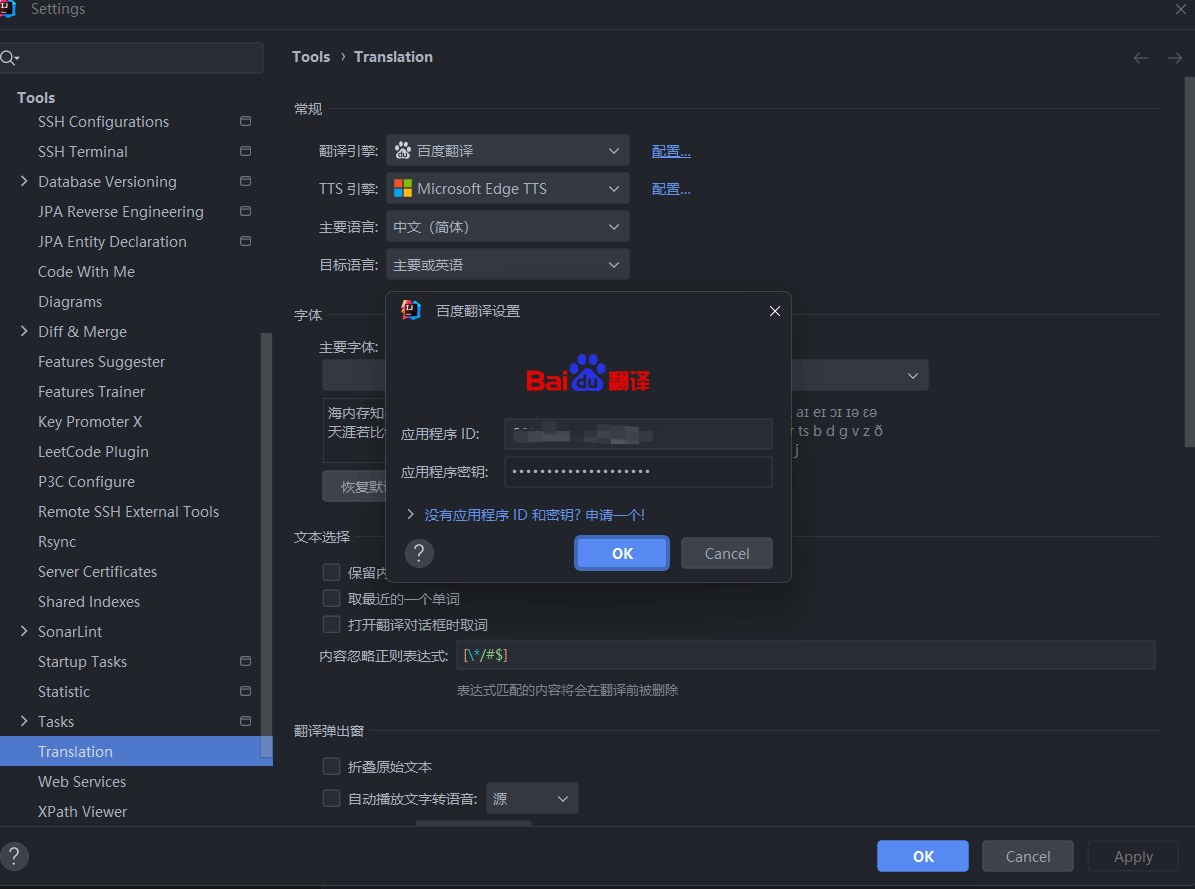
idea中配置Translation插件完成翻译功能
文章目录 idea下载插件配置有道云阿里云百度翻译开放平台 idea下载插件 idea中安装Translation插件 使用方法:右下角选择翻译引擎,鼠标选中想翻译的部分,右键翻译即可 之前一直用的微软的翻译,不需要配置,但是最近微软…...

如何看待:低代码开发平台的兴起无需经验?
在当今快速发展的技术时代,软件开发的需求日益增长,而专业开发人员的数量却远远跟不上需求的步伐。为了解决这一矛盾,低代码开发平台应运而生,它通过提供可视化的开发环境和拖拽式的编程方式,使得没有编程经验的用户也…...

OpenCV-轮廓检测
文章目录 一、简介1. 意义2.具体步骤 二、代码实现三、总结 一、简介 1. 意义 在OpenCV中,轮廓检测是图像处理中一个非常重要的环节,它允许我们识别图像中的形状。这个过程通常涉及几个步骤:读取图像、转换为灰度图、应用阈值处理ÿ…...

vue页面使用自定义字体
一、准备好字体文件 一般字体问价格式为 .tff,可以去包图网等等网站去下载,好看的太多了!!! 下载下来就是单个的 .tff文件,下载下来后可以进行重命名,但是不要改变他的后缀名,我把他…...
)
C++——list常见函数的使用和模拟实现(2)
在list的上一篇博客里实现了list基本的初始化、插入数据、删除数据的基本功能,这些功能的实现方式只是在原先链表的实现里加入了模版而已,但是list作为一个容器,它还有一个基础的东西——迭代器。list的迭代器和之前实现的string和vector很大…...

C 标准库 - `<float.h>`
C 标准库 - <float.h> 概述 <float.h> 是 C 标准库中的一个头文件,它定义了与浮点数类型相关的宏。这些宏提供了关于浮点数的属性信息,如精度、最小和最大值、以及舍入误差等。这个头文件对于需要精确控制浮点数行为的程序非常有用&#x…...

【机器人工具箱Robotics Toolbox开发笔记(二)】Matlab中机器人工具箱的下载与安装
Matlab机器人工具箱(Robotics Toolbox)可从Peter Corke教授提供的网站上免费下载。网址为:http://www.petercorke.com/Robotics_Toolbox.html。 图1 网站所提供的机器人工具箱版本 在Downloading the Toolbox栏目中单击here按钮进入下载页面,然后在该页面中填写国家、组织…...

ROS2 Nav2 - Smac 规划器
系列文章目录 前言 SmacPlanner 是 Nav2 Planner 服务器的插件。它目前包括 3 个不同的插件: SmacPlannerHybrid:高度优化的完全可重新配置的 Hybrid-A* 实现,支持 Dubin 和 Reeds-Shepp 模型(足式、阿克曼和汽车模型)…...
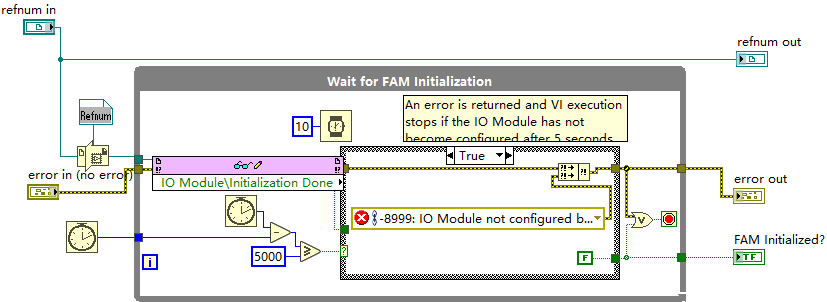
LabVIEW环境中等待FPGA模块初始化完成
这个程序使用的是LabVIEW环境中的FPGA模块和I/O模块初始化功能,主要实现等待FAM(Field-Programmable Gate Array Module,FPGA模块)的初始化完成,并处理初始化过程中的错误。让我们逐步分析各部分的功能: 1.…...

手机TF卡格式化后数据恢复:方法、挑战与预防措施
在现代生活中,手机已经成为我们不可或缺的一部分,而TF卡(即MicroSD卡)作为手机存储的扩展,更是承载了我们大量的重要数据。然而,不慎的格式化操作往往导致数据丢失,给用户带来不…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
