pytorch torch.norm函数介绍
torch.norm 函数用于计算张量的范数(norm),可以理解为张量的“长度”或“大小”。根据范数的不同类型,它可以衡量不同的张量性质。该函数可以计算 向量 和 矩阵 的多种范数,如 L1范数、L2范数、无穷范数 等。
1. 函数签名
torch.norm(input, p='fro', dim=None, keepdim=False, dtype=None, out=None)
-
input: 需要计算范数的输入张量。
-
p: 范数的类型,常用值包括:
'fro'(默认值):Frobenius 范数(矩阵的元素平方和开平方,类似于 L2 范数)。p=1:L1 范数,元素的绝对值和。p=2:L2 范数,元素的平方和的平方根(也称为欧几里得范数)。p=float('inf'):无穷范数,张量元素的最大绝对值。- 其他 p 值可以表示不同的 p-范数(如 p=3 表示元素的三次方和的开三次方根)。
-
dim: 计算范数的维度。如果不指定维度,默认计算整个张量的范数。可以指定一个或多个维度。
-
keepdim: 是否保持计算后的张量的维度。
-
dtype: 可选,指定输出张量的数据类型。
-
out: 可选,用于存储输出的张量。
2. 范数类型的解释
3. 示例
计算向量的 L2 范数
import torcha = torch.tensor([3.0, 4.0])# 计算 L2 范数 (默认 p=2)
l2_norm = torch.norm(a)
print(f"L2 范数: {l2_norm.item()}")
计算 L1 范数
# 计算 L1 范数
l1_norm = torch.norm(a, p=1)
print(f"L1 范数: {l1_norm.item()}")
计算无穷范数
# 计算无穷范数
inf_norm = torch.norm(a, p=float('inf'))
print(f"无穷范数: {inf_norm.item()}")
计算矩阵的 Frobenius 范数
b = torch.tensor([[1.0, 2.0], [3.0, 4.0]])# 计算 Frobenius 范数
fro_norm = torch.norm(b, p='fro')
print(f"Frobenius 范数: {fro_norm.item()}")
指定维度计算范数
# 计算矩阵每一行的 L2 范数
row_norms = torch.norm(b, p=2, dim=1)
print(f"每行的 L2 范数: {row_norms}")
4. 应用场景
- L1 范数:用于稀疏性约束或正则化(Lasso 回归等)。
- L2 范数:广泛用于优化问题、深度学习中的权重正则化、距离测量等。
- 无穷范数:用于估计最大值(如误差上界的评估)。
- Frobenius 范数:通常用于矩阵运算中,衡量矩阵的整体大小。
通过 torch.norm 函数,可以灵活选择不同的范数类型和维度,满足各种计算需求。
相关文章:

pytorch torch.norm函数介绍
torch.norm 函数用于计算张量的范数(norm),可以理解为张量的“长度”或“大小”。根据范数的不同类型,它可以衡量不同的张量性质。该函数可以计算 向量 和 矩阵 的多种范数,如 L1范数、L2范数、无穷范数 等。 1. 函数…...

【lc_hot100】刷题心得
链表 二叉树 二叉树相关的题目基本都有个基本的框架,基本框架就是二叉树的四种遍历方法:前序遍历、中序遍历、后序遍历、层序遍历 往往常用的是前序遍历和中序遍历 图 图跟二叉树一样都有自己的的基本框架,基本框架就是图的两种遍历方法&am…...

FANUC 数控 A06B-6058-H227 伺服放大器
发那科伺服放大器是一种控制电机的电子装置,属于电机控制系统的一部分,用于将输入信号放大并转换成电动机可以理解的信号,从而实现运动控制和定位。 发那科伺服放大器的主要作用包括: 实现运动控制:通过控制…...
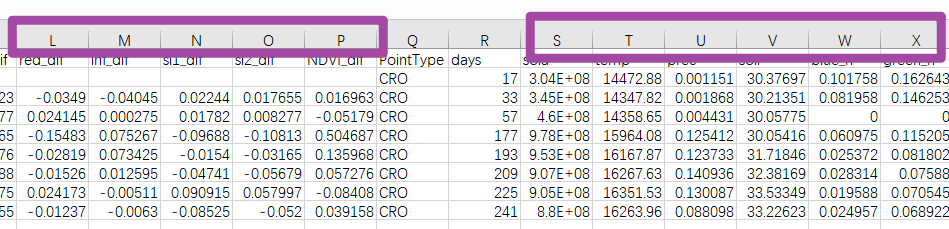
Python将表格文件中某些列的数据整体向上移动一行
本文介绍基于Python语言,针对一个文件夹下大量的Excel表格文件,对其中的每一个文件加以操作——将其中指定的若干列的数据部分都向上移动一行,并将所有操作完毕的Excel表格文件中的数据加以合并,生成一个新的Excel文件的方法。 首…...

基于YOLOv8的PCB缺陷检测算法,加入一种基于内容引导注意力(CGA)的混合融合方案(一)
💡💡💡本文内容:针对基于YOLOv8的PCB缺陷检测算法进行性能提升,加入各个创新点做验证性试验。 1)提出了一种基于内容引导注意力(CGA)的混合融合方案,mAP0.5由原始的0.966提升至0.975 1.PCB缺陷…...

如何在红米手机中恢复已删除的照片?(6 种方式可供选择)
凭借出色的相机和实惠的价格,小米红米系列已成为全球知名品牌。但是,最近有些人抱怨他们在 红米设备上丢失了许多珍贵的图片或视频,并希望弄清楚如何从小米手机恢复已删除的照片。好吧,在小米设备上恢复已删除的视频/照片并不难。…...

嵌入式实时操作系统(RTOS):原理、应用与发展
摘要:本文围绕嵌入式实时操作系统(RTOS)展开。首先介绍嵌入式系统与实时操作系统的概念,阐述嵌入式 RTOS 的体系结构。接着分析其关键特性,包含任务管理(如任务的创建与删除、调度、同步与通信)…...

C#里使用位图容器BitArray
由于经常需要操作一些位表示的数据结构,那么就需要采用位图的管理方式。 在C#里就是使用BitArray来管理位图数据结构,这样就比较方便处理。 这个类可以有多种构造函数,可以满足绝大部分的要求。 比如从网络协议里传送过来的字节流,就可以直接写入到里面,就可以直接获取…...

如何在 Kali Linux 上安装 pip3
如何在 Kali Linux 上安装 pip3 在 Kali Linux 上安装 pip3 的过程非常简单。按照以下步骤,你可以轻松完成安装并开始使用 pip3 管理 Python 软件包。 步骤 1:打开终端 首先,打开你的 Kali Linux 终端。 步骤 2:更新软件包列表…...

5.2 排列与代数余子式
一、求行列式的方法 计算机是利用主元计算行列式的。本节介绍其它两种计算行列式的方法。一是 “大公式”(big formula),它使用了全部 n ! n! n! 个排列计算;二是 “代数余子式公式”(cofactor formula)&…...

java框架第五课(终极版本)SpringBoot
一.关于SpringBoot (1)回忆Spring 传统的Spring由Spring 框架(ioc,aop)加mybatis加Springweb组成,虽然相比原生的java程序Spring框架帮我们大大减少了代码量,减少了冗余,提高了开发效率但是由于Spring框架下的配置和相关的jar包依赖过多&am…...

聚类案例——汽车是否值得购买
对汽车是否值得购买,进行聚类分析: 1、数据指标解释: buying, 购买费用 maint, 维修费用 doors, 车门数量 person, 乘坐人数 lug_boot, 行李箱容量 safety, 安全性 2、对数据进行转换 将字符串转换映射量化为数字 数据加载:…...

网络编程9.10
使用数据库完成工人管理系统: ubuntuubuntu:DB$ ubuntuubuntu:DB$ cat 2.c #include <myhead.h> #include <sqlite3.h> #include <string.h>typedef struct {int id;char name[20];double salary; } Worker;int do_insert(sqlite3 *ppDb) {Worker work;pri…...
如何在SQL Server中恢复多个数据库?
一次性恢复多个 SQL数据库吗可以吗? "是的,可以一次性恢复多个 SQL 数据库。通常情况下,只要备份文件的名称与相应的数据库匹配,且没有附加的日期或时间信息,就可以通过有效的 T-SQL 脚本来完成恢复。如果你希望…...
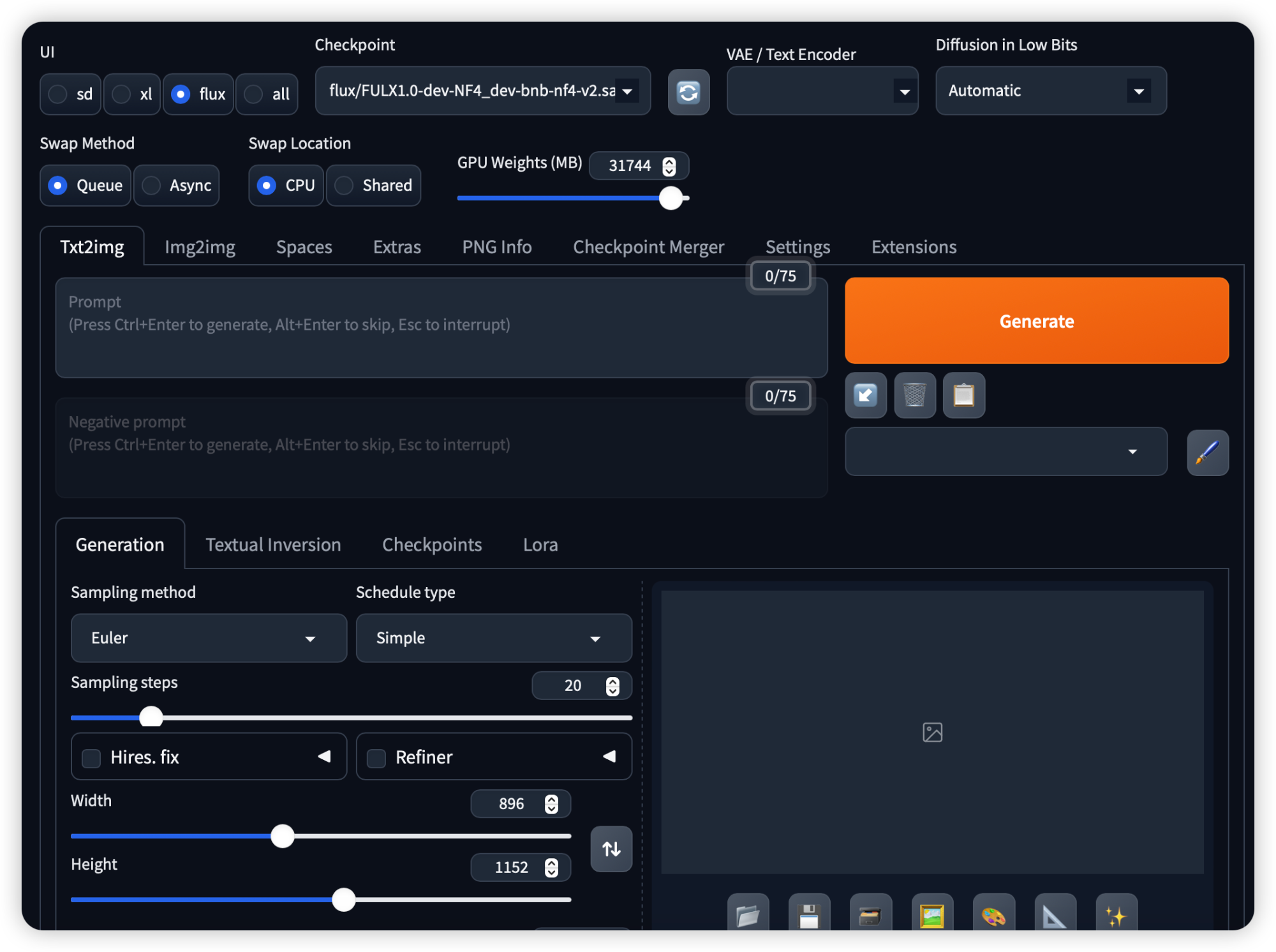
炸裂!新版 SD WebUI Forge 出图速度更快!支持最新Flux 模型!(保姆级安装教程)
大家是不是经常为SD WebUI卡顿、爆显存而苦恼?一启动SD 电脑就开始发烫, 尤其低显存用户屡屡"中招",不得不一遍遍重启。作为AI绘画的必备工具,WebUI却还有这么多"坑",着实让人不爽!😠 好消息是,…...

laserOdometry.cpp源码注释
本博客用于a-loam源码学习,用于和slam初学者一起学习。 #include <cmath>#include <nav_msgs/Odometry.h>#include <nav_msgs/Path.h> //这两行代码是C中包含头文件的指令,它们用于在ROS(Robot Operating System…...

STM32时钟配置图详解
一图概述: 左侧输入时钟源 Input Frequency (LSE/LSI/HSI/HSE) LSE (Low-Speed External):外部32.768 kHz晶体振荡器,通常用于RTC(实时时钟)。LSI (Low-Speed Internal):内部低速时钟,频率为…...

Vscode——调试时,修改变量值
第一步:点击变量,鼠标右键 第二步:点击 设置值...
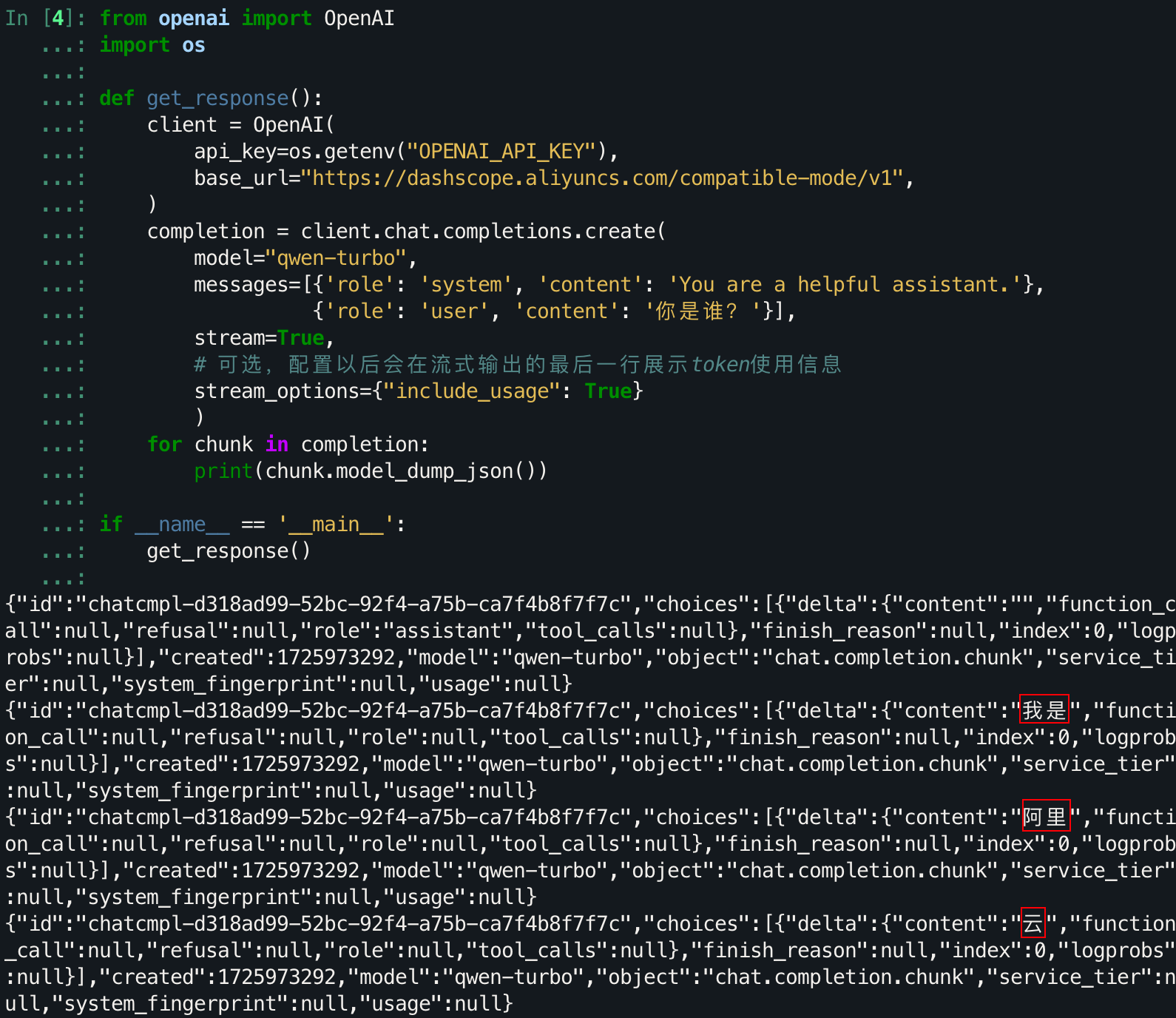
1. 初识LLM API:环境配置与多轮对话演示
其实AI应用并不是一个什么很高大上的东西,你可以将它当作一个文字的“调库”行为,“调库”只需要知道库名就行了,这里实际也是如此。甚至你只需要知道你想问什么,将你的消息作为输入,就能从大模型得到输出。而这个“库…...

【AI编程助手】VsCode插件--通义灵码
目录 摘要 一、插件安装 二、“通义灵码” 使用 三、官网教程 四、总结 五、参考信息 摘要 通义灵码是一款强大的 AI 编程助手。它能够理解编程相关的复杂逻辑,为开发者提供高效、准确的代码生成与优化建议。在编程过程中,它可以辅助处理各种任务&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
