出处不详 取数游戏
目录
- 取数游戏
- 题目描述
- 背景
- 输入
- 输出
- 数据范围
- 题解
- 解法
- 优化
- 打赏
取数游戏
题目描述
背景
两人将 n n n个正整数围成一个圆环,规则如下:
- 第一名玩家随意选取数字;
- 第二名玩家从与第一名玩家相邻的两个数字中选择一个;
- 而后依次在到目前为止所取的任何数字旁边取一个数字,直到数字用完,选择更多奇数的玩家获胜
第一个选取数字的玩家想知道他能做出多少不同的第一步,使他有机会获胜
输入
- 第一行一个整数 n n n;
- 第二行 n n n个整数 n u m i num_i numi,表示围在地上的数字
输出
输出一个整数,表示有机会获胜的不同的第一步的数量
数据范围
1 ≤ n ≤ 100 , 1 ≤ n u m i ≤ 1000 1 \le n \le 100 , 1 \le num_i \le 1000 1≤n≤100,1≤numi≤1000
题解
解法
由于要算的是有机会获胜的不同第一步的数量,所以对于每个可能的第一步,只要后续所有选择情况中,第一名玩家获得最多奇数的那一种情况下超过了第二名玩家即可
为此可以定义一个二维数组 f [ ] [ ] f[][] f[][], f [ i ] [ j ] f[i][j] f[i][j]表示在第 i i i至 j j j个数已经被选择后( i i i可以大于 j j j),直到所有数都被选择,该过程中第一名得到的奇数最多可超出第二名多少
使用动态规划来更新这个数组,先由大到小枚举已经被选的数的数量 i ( n − 1 ≥ i ≥ 1 ) i(n - 1 \ge i \ge 1) i(n−1≥i≥1),再枚举被选数的区间,定义变量 l , r l , r l,r表示枚举到的区间的左右边界下标,变量 l l , r r ll , rr ll,rr分别表示表示圆环中 l l l的前一个数和 r r r的后一个数,再根据 i + 1 i + 1 i+1的奇偶判断接下来是第一名还是第二名玩家选数,这样就得到了状态转移方程: f [ l ] [ r ] = m a x ( f [ l l ] [ r ] ± n u m [ l l ] % 2 , f [ l ] [ r r ] ± n u m [ r r ] % 2 ) f[l][r] = max(f[ll][r] \pm num[ll] \% 2 , f[l][rr] \pm num[rr] \% 2) f[l][r]=max(f[ll][r]±num[ll]%2,f[l][rr]±num[rr]%2)( i + 1 i + 1 i+1为奇时取 + + +,反之取 − - −)
全部更新完后,统计满足 f [ i ] [ i ] + n u m [ i ] % 2 > 0 f[i][i] + num[i] \% 2 > 0 f[i][i]+num[i]%2>0(因为第一个数一定是第一名玩家选的)的 i i i有几个即可
代码如下:
#include<cstdio>#define il inlineconst int M = 105;int f[M][M], num[M];int main() {int n, ans = 0;scanf("%d%", &n);for(int i = 1; i <= n; ++i) scanf("%d%", &num[i]);for(int i = n - 1; i >= 1; --i) {if(i % 2 ^ 1) //等于(i + 1)%2for(int l = 1, r = i; l <= n; ++l) {int ll = l - 1 ? l - 1 : n, rr = r + 1 <= n ? r + 1 : 1;int s1 = f[ll][r] + num[ll] % 2, s2 = f[l][rr] + num[rr] % 2;f[l][r] = s1 > s2 ? s1 : s2, r = rr;}else for(int l = 1, r = i; l <= n; ++l) {int ll = l - 1 ? l - 1 : n, rr = r + 1 <= n ? r + 1 : 1;int s1 = f[ll][r] - num[ll] % 2, s2 = f[l][rr] - num[rr] % 2;f[l][r] = s1 < s2 ? s1 : s2, r = rr;}}for(int i = 1; i <= n; ++i) ans += num[i] % 2 + f[i][i] > 0;printf("%d", ans);return 0;
}
优化
可以发现全程只用到了 n u m [ i ] num[i] num[i]的奇偶性,所以可以在输入时就把 n u m [ i ] num[i] num[i]处理成 0 0 0或 1 1 1,这样 n u m [ ] num[] num[]只需要为 b o o l bool bool数组
代码如下:
#include<cstdio>#define il inlineconst int M = 105;il int read() {int x = 0;char c = getchar();while(c < '0' || c > '9') c = getchar();while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();return x;
}bool num[M];
int f[M][M];int main() {int n = read(), ans = 0;for(int i = 1; i <= n; ++i) num[i] = read() % 2;for(int i = n - 1; i >= 1; --i) {if(i % 2 ^ 1)for(int l = 1, r = i; l <= n; ++l) {int ll = l - 1 ? l - 1 : n, rr = r + 1 <= n ? r + 1 : 1;int s1 = f[ll][r] + num[ll], s2 = f[l][rr] + num[rr];f[l][r] = s1 > s2 ? s1 : s2, r = rr;}else for(int l = 1, r = i; l <= n; ++l) {int ll = l - 1 ? l - 1 : n, rr = r + 1 <= n ? r + 1 : 1;int s1 = f[ll][r] - num[ll], s2 = f[l][rr] - num[rr];f[l][r] = s1 < s2 ? s1 : s2, r = rr;}}for(int i = 1; i <= n; ++i) ans += num[i] + f[i][i] > 0;printf("%d", ans);return 0;
}
打赏
制作不易,若有帮助,欢迎打赏!


相关文章:

出处不详 取数游戏
目录 取数游戏题目描述背景输入输出数据范围 题解解法优化 打赏 取数游戏 题目描述 背景 两人将 n n n个正整数围成一个圆环,规则如下: 第一名玩家随意选取数字;第二名玩家从与第一名玩家相邻的两个数字中选择一个;而后依次在…...

拉取ros2_control_demos存储库
目录 克隆存储库 方法 1: 使用 git clone 和 rosdep 安装依赖 方法 2: 使用 vcs 工具管理多个存储库 区别总结 rosdep 和 APT 的关系 网络问题 安装依赖 克隆存储库 方法 1: 使用 git clone 和 rosdep 安装依赖 下载存储库: mkdir -p ~/ros2_ws/src cd ~/ros…...

Apache Doris Flink Connector 24.0.0 版本正式发布
亲爱的社区伙伴们,Apache Doris Flink Connector 24.0.0 版本已于 2024 年 9 月 5 日正式发布。该版本新增了对 Flink 1.20 的支持,并支持通过 Arrow Flight SQL 高速读取 Doris 中数据。此外,整库同步所依赖的 FlinkCDC,也需升级…...

语音控制小夜灯的实现方案介绍
语音控制小夜灯的实现方案组成部分 语音控制小夜灯的实现方案主要包括硬件组装和软件编程两个部分。 硬件组装涉及将语音声控模块、灯泡、USB连接线等组件正确连接。首先,使用螺丝刀和螺丝将四个隔离柱固定在底板四个拐角处,同时将语音声控模…...

万龙觉醒免费辅助:VMOS云手机辅助巴克尔阵容搭配攻略!
《万龙觉醒》是一款策略类手游,选择合适的英雄阵容搭配能够极大提升战斗效果。而借助VMOS云手机的辅助功能,玩家可以更加轻松地管理游戏进程,优化操作体验。以下是VMOS云手机的三大核心功能,帮助你更好地掌控《万龙觉醒》战局。 V…...

【English】长难句翻译
这里写目录标题 技巧知识点1. 定语从句 和 状从区别2. 定从 修饰词3. who 和 whom 区别4. 除了定从、状从,还有啥?5. 怎么在长难句快速定位到主谓宾而不被各种从句中的动词影响判断6. 没有,的那种一大堆从句连起来的长难句怎么办7. 时态怎么放在翻译里总结技巧 知识点 1. 定语…...

npm login 或者 npm publish 超时timeout
场景:空闲时间想自己尝试下npm发布包,毕竟这东西可以不用,但不能不会 步骤很简单 1.npm login 2.npm publish 这里有个坑。。。因为想发布到npm上,所以这里的镜像源要换回https://registry.npmjs.org,不能使用淘宝镜像…...
)
Python的openpyxl使用記錄(包含合併單元格,圖片下載和圖片插入,設置邊框,設置背景顏色)
背景 因為公司最近要求我做一份自動化導出報告,內容有點多,為了省事,我選用了python,後面估計要自建在線辦公系統,這個後續再講 需要的庫 openpyxl 和Pandas 開始 Execl導入 from openpyxl import load_workbook …...

基于springboot+vue实现的在线商城系统
系统主要功能: (1)商品管理模块:实现了商品的基本信息录入、图片上传、状态管理等相关功能。 (2)商品分类模块:实现了分类的增删改查、分类层级管理、商品分类的关联等功能。 (3&…...

fastjson漏洞--以运维角度进行修复
文章目录 前言一、漏洞详情二、修复过程1.通过脚本方式修复1.1.脚本修复原理1.2.脚本演示1.3.执行脚本 2. 手动升级包2.1.修复步骤2.2.遇到的问题 前言 该漏洞是三个月前由安全团队扫描出来的,主要影响是: FastJSON是阿里巴巴的开源JSON解析库,它可以解…...
82页精品PPT | 构建数字化工厂的智能制造-数字化智能制造
新模式、新技术 、新制造的挑战 中国制造业正处于转型升级的关键时期,面临着多方面的挑战。创新能力不足导致产品同质化严重,缺乏核心竞争力;质量管理水平参差不齐,影响着产品的可靠性和安全性;品牌价值不高ÿ…...

Python的10个日期和时间操作的实用技巧
在Python中,处理日期和时间是一项常见且重要的任务。datetime模块提供了丰富的功能来执行这些操作。以下是10个日期和时间操作的实用技巧及其代码演示: 1. 获取当前日期和时间 from datetime import datetimenow datetime.now() print(f"当前日期…...

关于大模型在产品开发中所面临的问题,利用大模型技术解决很简单!
“ 具体问题具体分析,大模型技术没有统一的解决方案 ” 有人说2024年是大模型应用的元年,而大模型在未来的发展潜力毋庸置疑,这也就意味着人工智能技术是下一个风口,因此各种各样基于大模型技术的创业公司如雨后春笋般涌现。 从…...

SpringBoot2:请求处理原理分析-利用内容协商功能实现接口的两种数据格式(JSON、XML)
文章目录 一、功能说明二、案例实现1、基于请求头实现2、基于请求参数实现 一、功能说明 我们知道,用ResponseBody注解标注的接口,默认返回给页面的是json数据。 其实,也可以返回xml结构的数据给页面。 这一篇就来实现一下这个小功能。 二、…...

BUUCTF 之Basic 1(BUU LFI COURSE 1)
1、启动靶场,会生成一个URL地址,打开给的URL地址,会看到一个如下界面 可以看到是一个PHP文件,非常的简单,就几行代码,判断一下是否有一个GET的参数,并且是file名字,如果是并且加载&a…...

Android 蓝牙三方和动态权限三方
记录一下最近用到的简单的框架 蓝牙 FastBle:Android BLE通信库的介绍与高级用法 - 简书 https://github.com/Jasonchenlijian/FastBle 动态权限: GitHub - googlesamples/easypermissions: Simplify Android M system permissions 位置权限举例,arrayOf中多个…...

点餐|基于java的电子点餐系统小程序(源码+数据库+文档)
电子点餐系统|小程序|在线点餐 目录 基于java的电子点餐系统小程序 一、前言 二、系统设计 三、系统功能设计 系统功能实现 前台: 后台: 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: …...

18、Gemini-Pentest-v1
难度 中 (个人认为是高) 目标 root权限 一个flag 靶机启动环境为VMware kali 192.168.152.56 靶机 192.168.152.64 信息收集 突破点大概就是web端了 web测试 访问主页直接就是目录遍历 不过进去后是一个正常的网页 简单的试了几个弱口令无果继续信息…...
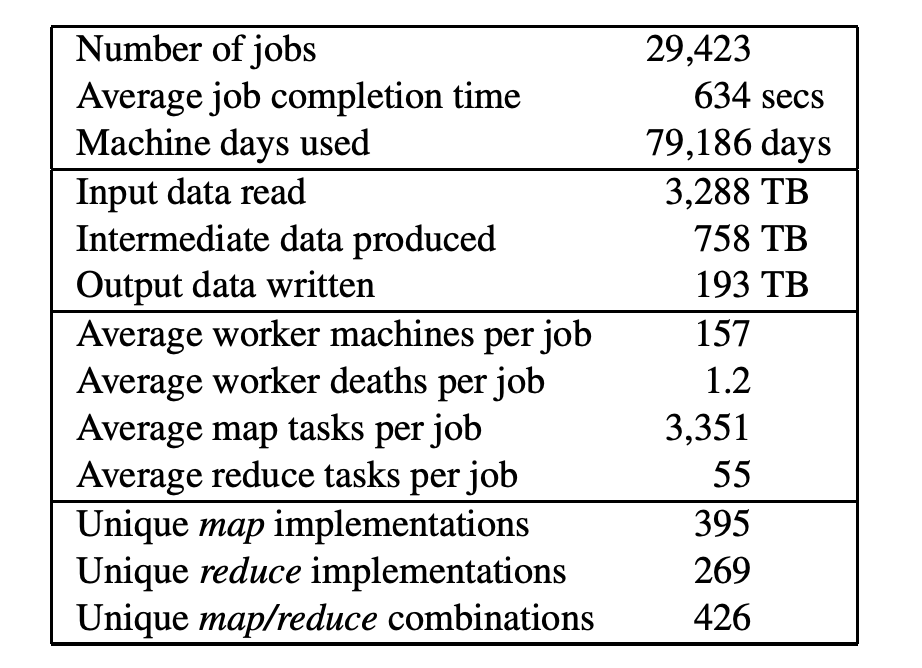
MIT6.824 课程-MapReduce
MapReduce:在大型集群上简化数据处理 概要 MapReduce是一种编程模型,它是一种用于处理和生成大型数据集的实现。用户通过指定一个用来处理键值对(Key/Value)的map函数来生成一个中间键值对集合。然后,再指定一个reduce函数, 它用…...

7个 C# 高阶用法详解:从基础到实战
C# 高阶用法详解:从基础到实战 在实际开发中,C# 提供了很多高级特性和设计模式,帮助我们写出更加简洁、灵活和高效的代码。本篇将深入探讨 C# 中的高阶用法,通过丰富的示例,带你掌握这些工具的精髓。 1. LINQ&#x…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
