光纤的两种模式
光纤主要分为两种模式:单模光纤(Single-Mode Fiber, SMF)和多模光纤(Multi-Mode Fiber, MMF)。这两种光纤在传输特性、应用场景以及传输距离上存在显著差异。12
单模光纤
定义:单模光纤是一种只用来传输一种模式光(但可以含有多种波长的光)的光纤。
特点:
纤芯直径较小,通常为8~10μm,光缆外径为125μm。
允许与光纤轴方向一致的光线通过,即只允许通过一个模式的光。
适用于长距离、高速率的数据传输。
应用:主要用于长距离通信、城域网、广域网等。
多模光纤
定义:多模光纤是一种可以传输多种模式光波的光纤。
特点:
纤芯直径较大,一般为50μm或62.5μm。
允许光以多个入射角射入并传播。
传输距离较短,一般在500米以内。
适用于短距离通信、局域网等。
应用:主要用于建筑物内的布线、数据中心内部连接等。
区分方法
颜色区分:单模光纤通常为黄色,多模光纤多为橘红色或灰色。
传输距离和速率:单模光纤适用于长距离、高速率传输,而多模光纤适用于短距离、较低速率传输。
选择依据
根据传输距离和速率要求选择合适类型的光纤。长距离、高速率通信选择单模光纤;短距离、低速率通信选择多模光纤。
通过了解单模光纤和多模光纤的定义、特点、应用场景以及区分方法,可以更好地根据实际需求选择合适的光纤类型,以满足不同的通信需求。
相关文章:

光纤的两种模式
光纤主要分为两种模式:单模光纤(Single-Mode Fiber, SMF)和多模光纤(Multi-Mode Fiber, MMF)。这两种光纤在传输特性、应用场景以及传输距离上存在显著差异。12 单模光纤 定义:单模光纤…...
SpringMVC的初理解
1. SpringMVC是对表述层(Controller)解决方案 主要是 1.简化前端参数接收( 形参列表 ) 2.简化后端数据响应(返回值) 1.数据的接受 1.路径的匹配 使用RequestMapping(可以在类上或在方法上),支持模糊查询,在内部有method附带…...
Python 基本库用法:数学建模
文章目录 前言数据预处理——sklearn.preprocessing数据标准化数据归一化另一种数据预处理数据二值化异常值处理 numpy 相关用法跳过 nan 值的方法——nansum和nanmean展开多维数组(变成类似list列表的形状)重复一个数组——np.tile 分组聚集——pandas.…...

Android Greendao的数据库复制到设备指定位置
方法如下: private void export() {// 确保您已经请求并获得了WRITE_EXTERNAL_STORAGE权限// 获取要储存的设备路径String picturesDirPath Environment.getExternalStoragePublicDirectory(Environment.DIRECTORY_PICTURES).getAbsolutePath();// 在公共目录下创建…...
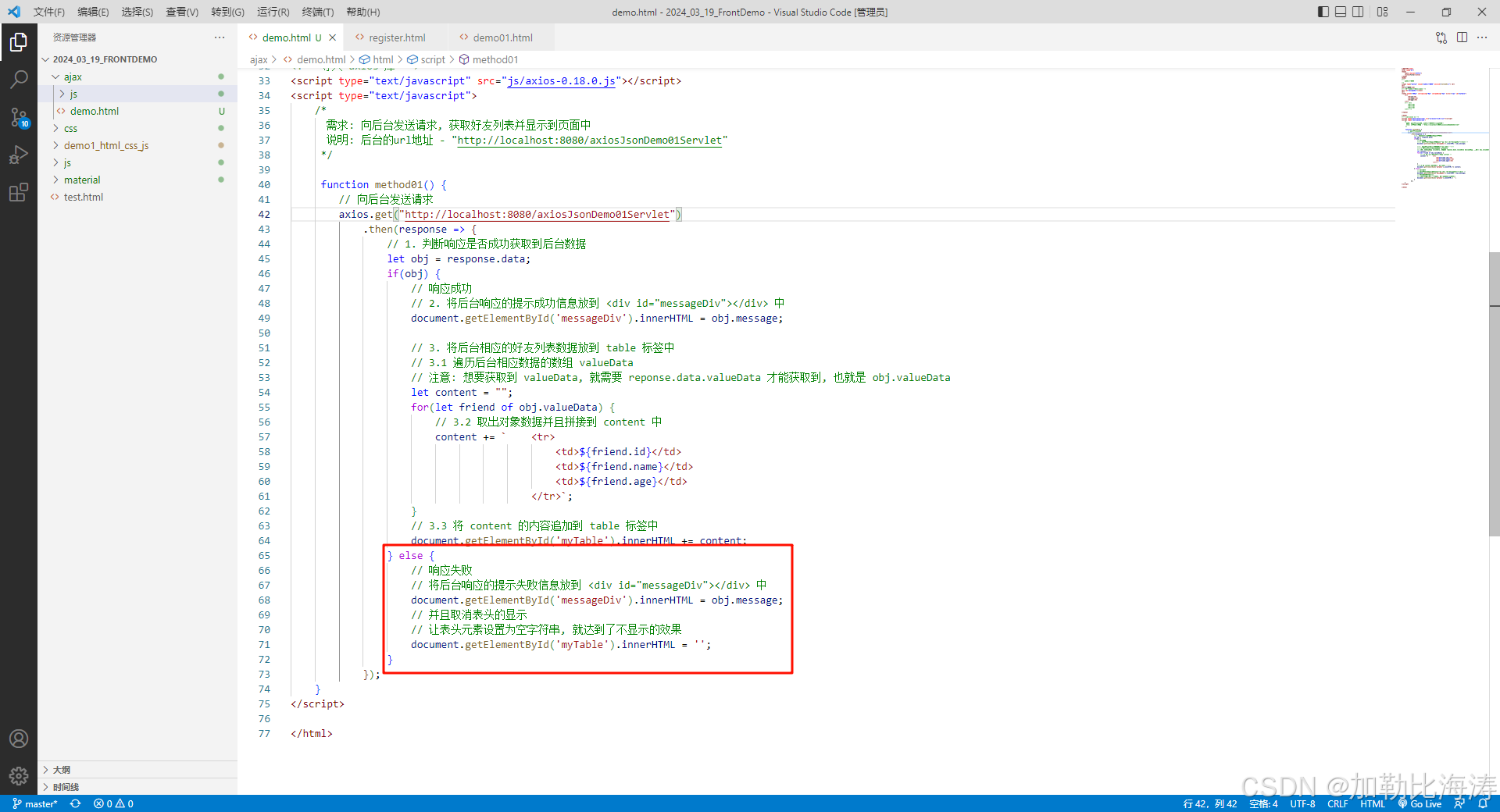
Ajax 揭秘:异步 Web 交互的艺术
Ajax 揭秘:异步 Web 交互的艺术 一 . Ajax 的概述1.1 什么是 Ajax ?1.2 同步和异步的区别1.3 Ajax 的应用场景1.3.1 注册表单的用户名异步校验1.3.2 内容自动补全 二 . Ajax 的交互模型和传统交互模型的区别三 . Ajax 异步请求 axios3.1 axios 介绍3.1.1 使用步骤3…...

TitleBar:打造高效Android标题栏的新选择
在Android应用开发中,标题栏是用户界面的重要组成部分。一个好的标题栏不仅能够提升应用的专业感,还能增强用户体验。然而,传统的标题栏实现方式往往存在代码冗余、样式不统一、性能开销大等问题。今天,我们将介绍一个名为TitleBa…...

Lua协同程序Coroutine
Lua 协同程序(Coroutine) 定义 Lua 协同程序(Coroutine)与线程类似:拥有独立的堆栈、局部变量、指令指针,同时又与其它协同程序共享全局变量和其它大部分东西。 协同程序可以理解为一种特殊的线程,可以暂停和恢复其执行,从而允…...

【vue+帆软】帆软升级,从版本9升级到版本11,记录升级过程
帆软要升级,记录下过程 1、帆软官网地址必不可少,戳这里,跳转帆软官网 点击前端开发指南 点击JS API 跳转过来就是版本11 一直往下翻,在最底部有个2.2 在Web中使用,圈起来的就是要引入到index.html中的脚本 在项…...

linux从0到1 基础完整知识
1. Linux系统概述 Linux是一种开源操作系统,与Windows或macOS等操作系统不同,Linux允许用户自由地查看、修改和分发其源代码。以下是Linux系统的一些显著的优势。 稳定性和可靠性: 内核以其稳定性而闻名,能够持续运行数月甚至数…...

“人大金仓”正式更名为“电科金仓”; TDSQL-C支持回收站/并行DDL等功能; BigQuery支持直接查询AlloyDB
重要更新 1. “人大金仓”正式更名为“电科金仓”,完整名称“中电科金仓(北京)科技股份有限公司”,突出金仓是中国电子科技集团有限公司在基础软件领域产品( [1] ) 。据悉人大金仓在上半年营收入为9056万元,净利润约21…...

大模型微调 - 用PEFT来配置和应用 LoRA 微调
大模型微调 - 用PEFT来配置和应用 LoRA 微调 flyfish PEFT(Parameter-Efficient Fine-Tuning)是一种参数高效微调库,旨在减少微调大型预训练模型时需要更新的参数量,而不影响最终模型的性能。它支持几种不同的微调方法ÿ…...
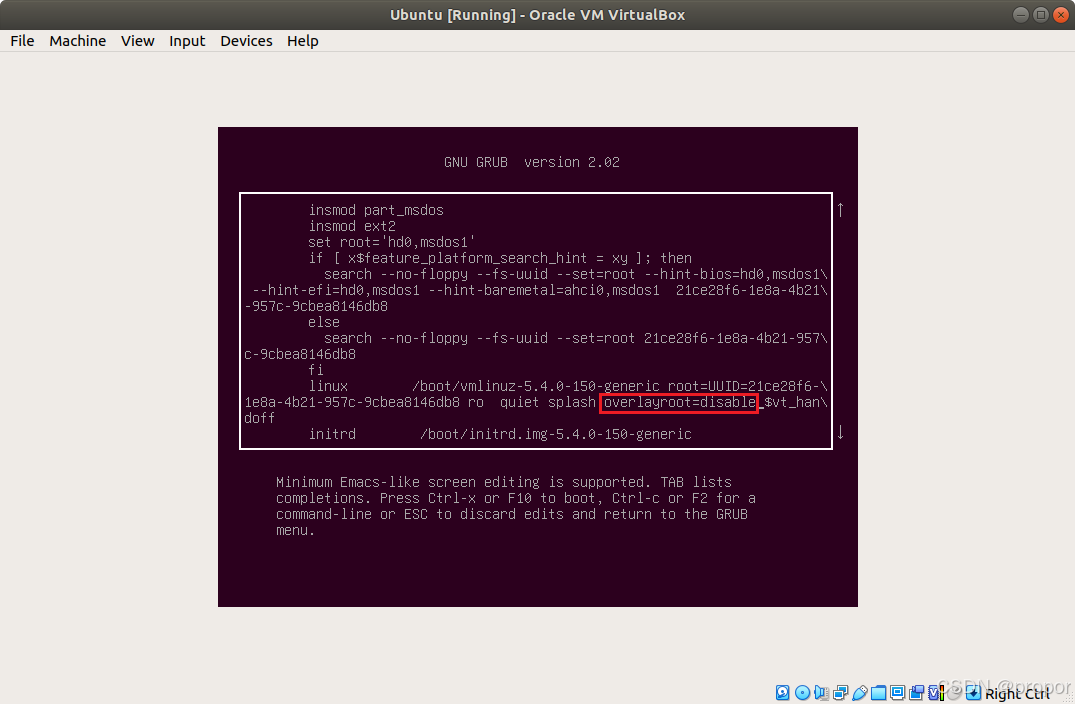
Ubuntu构建只读文件系统
本文介绍Ubuntu构建只读文件系统。 嵌入式系统使用过程中,有时会涉及到非法关机(比如直接关机,或意外断电),这可能造成文件系统损坏,为了提高系统的可靠性,通常将根文件系统设置为只读…...

【黑金系】金融UI/UX体验设计师面试作品集 Figma源文件分享
在数字金融时代,UI/UX体验设计师扮演着至关重要的角色。他们不仅塑造着产品的界面,更引领着用户的使用体验。我们的面试作品集,正是这样一部展现金融UI/UX设计魅力的宝典。 这套作品集汇聚了众多经典案例,每一处设计都经过精心雕…...

Golang | Leetcode Golang题解之第392题判断子序列
题目: 题解: func isSubsequence(s string, t string) bool {n, m : len(s), len(t)f : make([][26]int, m 1)for i : 0; i < 26; i {f[m][i] m}for i : m - 1; i > 0; i-- {for j : 0; j < 26; j {if t[i] byte(j a) {f[i][j] i} else {…...

Liunx常用指令
1. 文件和目录管理 ls 用法:ls [选项] [文件/目录]示例:ls -l(以长列表格式显示),ls -a(显示所有文件,包括隐藏文件)。 cd 用法:cd [目录]示例:cd ..…...
如何使用清楚以及代替方法)
CSS基础:浮动(float)如何使用清楚以及代替方法
浮动元素在 CSS 中主要通过 float 属性来控制,影响元素的排列方式。浮动用于创建流式布局,常用于实现图文混排、布局列等效果。以下是浮动元素的相关属性和使用方法: 1. 基本浮动属性 float: 控制元素的浮动方向,可以设置为 left…...

margin重叠该怎么解决?
在CSS中,当两个或多个垂直相邻的块级元素(如<div>)的margin相遇时,它们不会叠加成两个margin的和,而是会取两个margin中的较大值,这种现象被称为“margin重叠”(margin collapsing&#x…...

Linux学习笔记(黑马程序员,前四章节)
第一章 快照 虚拟机快照: 通俗来说,在学习阶段我们无法避免的可能损坏Linux操作系统,如果损坏的话,重新安装一个Linux操作系统就会十分麻烦。VMware虚拟机支持为虚拟机制作快照。通过快照将当前虚拟机的状态保存下来,…...

tekton pipeline resources
PipelineResource 代表着一系列的资源,主要承担作为 Task 的输入或者输出的作用。它有以下几种类型: git:代表一个 git 仓库,包含了需要被构建的源代码。将 git 资源作为 Task 的 Input,会自动 clone 此 git 仓库。pu…...

使用Python实现多个PDF文件的合并
使用Python可以很方便地实现多个PDF文件的合并。我们可以使用PyPDF2库来完成这个任务。以下是一个实现PDF合并的Python脚本: import os from PyPDF2 import PdfMergerdef merge_pdfs(input_dir, output_filename):# 创建一个PdfMerger对象merger PdfMerger()# 获取…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
