3C电子胶黏剂在手机制造方面有哪些关键的应用
3C电子胶黏剂在手机制造方面有哪些关键的应用

3C电子胶黏剂在手机制造中扮演着至关重要的角色,其应用广泛且细致,覆盖了手机内部组件的多个层面,确保了设备的可靠性和性能。以下是电子胶在手机制造中的关键应用:
手机主板用胶:
芯片封装与粘接:使用环氧胶黏剂、导热导电胶,确保芯片与主板的稳定连接和散热。
灌封与散热:通过导热胶系列,提高热管理性能,减少热应力。
底部填充胶与UV胶:用于精确粘接和快速固化,增强电路板上元件的固定。
摄像头模组:
使用UV胶和低温固化环氧胶固定镜头与底座,确保光学性能不受影响。
侧按键与FPC天线:
UV胶和快干胶用于固定音量键、开关机键,以及FPC天线与机壳的粘接。
显示模组:
屏幕与边框粘接采用聚氨酯热熔胶、UV胶等,确保密封性和防尘防水。
光学透明胶(OCA):用于粘接触摸屏与LCD或OLED显示屏,提供高透明度和良好的触控性能。
摄像模组与马达连线:
UV胶、快干胶、环氧树脂胶用于摄像模组内部组件的粘接,以及马达连线的固定。
音腔盒与LOGO:
音腔盒盖固定使用UV胶、瞬干胶等,LOGO固定则偏好热熔压敏胶、有机硅胶黏剂。
粘接与固定:
双组分结构胶系列,提供高粘接强度,确保组件长期可靠性。
导热与散热:
导热凝胶系列,有效降低热阻,优化散热路径。
防护与密封:
UV湿气三防胶等,提供防潮、防腐蚀保护,增强电子组件的环境适应性。
密封胶用于电池盖粘接,确保电气绝缘和物理密封。
窄边距Underfill技术:
解决0.2mm极窄溢胶宽度挑战,确保芯片与PCB间无空穴、无气泡,采用斜式喷胶技术提高精度。
元器件包封:
Switch点胶技术,如tact switch的焊包封,实现100%通过率和精准溢胶控制。
窄边框热熔胶应用:
在屏幕边框粘接中,应对小间隙挑战,确保牢固粘接同时不影响显示效果。
这些应用不仅提高了手机的组装效率,还增强了产品的耐用性和用户使用体验。这些胶水和粘合剂的选择不仅基于它们的物理化学性能,还考虑到了环保要求以及生产工艺的兼容性。随着技术的不断进步,对电子胶的性能要求也在不断提高,包括更高的耐温性、更强的粘接力、更快的固化速度以及更好的环保特性,以适应更小型化、高性能的手机设计需求。
相关文章:

3C电子胶黏剂在手机制造方面有哪些关键的应用
3C电子胶黏剂在手机制造方面有哪些关键的应用 3C电子胶黏剂在手机制造中扮演着至关重要的角色,其应用广泛且细致,覆盖了手机内部组件的多个层面,确保了设备的可靠性和性能。以下是电子胶在手机制造中的关键应用: 手机主板用胶&…...
)
Oracle数据库中的动态SQL(Dynamic SQL)
Oracle数据库中的动态SQL是一种在运行时构建和执行SQL语句的技术。与传统的静态SQL(在编写程序时SQL语句就已经确定)不同,动态SQL允许开发者在程序执行过程中根据不同的条件或用户输入来构建SQL语句。这使得动态SQL在处理复杂查询、存储过程中…...

Python判断两张图片的相似度
在Python中,判断两张以numpy的ndarray格式存储的图片的相似度,通常可以通过多种方法来实现,包括但不限于直方图比较、像素差比较、结构相似性指数(SSIM)、特征匹配等。以下是一些常见方法的简要介绍和示例代码。 1. 像…...

MySQL高级功能-窗口函数
背景 最近遇到需求,需要对数据进行分组排序并获取每组数据的前三名。 一般涉及到分组,第一时间就是想到使用group by对数据进行分组,但这样分组,到最后其实只能获取到每组数据中的一条记录。 在需要获取每组里面的多条记录的时候…...

9.12总结
今天学了树状dp和tarjan 树状dp 树状dp,是一种在树形数据结构上应用的动态规划算法。动态规划(DP)通常用于解决最优化问题,通过将问题分解为相对简单的子问题来求解。在树形结构中,由于树具有递归和子结构的特性&…...

小众创新组合!LightGBM+BO-Transformer-LSTM多变量回归交通流量预测(Matlab)
小众创新组合!LightGBMBO-Transformer-LSTM多变量回归交通流量预测(Matlab) 目录 小众创新组合!LightGBMBO-Transformer-LSTM多变量回归交通流量预测(Matlab)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现LightGBMBO-Transformer-L…...

《CSS新世界》书评
《CSS新世界》是由张鑫旭所著,人民邮电出版社在2021年8月10日出版的一本专门讲解CSS3及其之后版本新特性的进阶读物。这本书是“CSS世界三部曲”中的最后一部,全书近600页,内容丰富,涵盖了CSS的全局知识、已有属性的增强、新布局方…...

python 实现euler modified变形欧拉法算法
euler modified变形欧拉法算法介绍 Euler Modified(改进)变形欧拉法算法,也被称为欧拉修改法或修正欧拉法(Euler Modified Method),是一种用于数值求解微分方程的改进方法。这种方法在传统欧拉法的基础上进…...

strcpy 函数及其缺点
目录 一、概念 二、strcpy 函数有什么缺点 1. 缺乏边界检查 2. 容易引发未定义行为 3. 不适合动态和未知长度的字符串操作 4. 替代方案的可用性 5. 效率问题 一、概念 strcpy 是 C 语言中的一个标准库函数,用于将源字符串复制到目标字符串中。它定义在 <…...

区块链-P2P(八)
前言 P2P网络(Peer-to-Peer Network)是一种点对点的网络结构,它没有中心化的服务器或者管理者,所有节点都是平等的。在P2P网络中,每个节点都可以既是客户端也是服务端,这种网络结构的优点是去中心化、可扩展…...
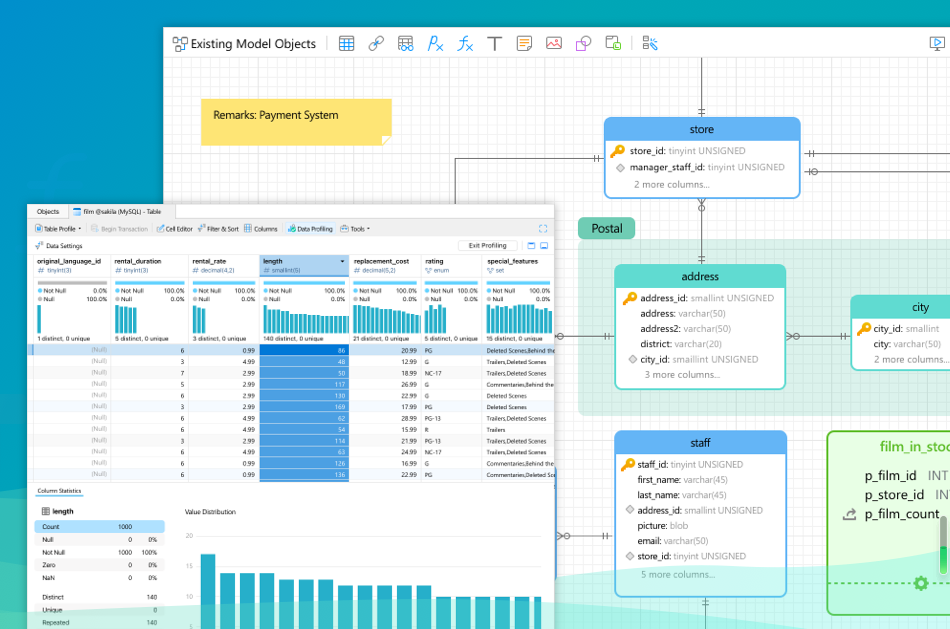
数据库管理的利器Navicat —— 全面测评与热门产品推荐
在数据库管理领域,Navicat无疑是一款深受欢迎的软件。作为一个强大的数据库管理和开发工具,它支持多种数据库类型,包括MySQL、MariaDB、MongoDB、SQL Server、Oracle、PostgreSQL等。本文将全面测评Navicat的核心功能,同时推荐几款…...

如何让Google收录我的网站?
其实仅仅只是收录,只要在GSC提交网址,等个两三天,一般就能收录,但收录是否会掉,这篇内容收录了是否有展现,排名,就是另外一个课题了,如果不收录,除了说明你的网站有问题&…...

03 Flask-添加配置信息
回顾之前学习的内容 02 Flask-快速上手 Flask 中最简单的web应用组成 1. 导入核心库 Flask from flask import Flask2. 实例化 web应用 注意:不要漏了 app Flask(__name__) 中的 __name__ 表示:是从当前的py文件实例化 app Flask(__name__)3. 创…...
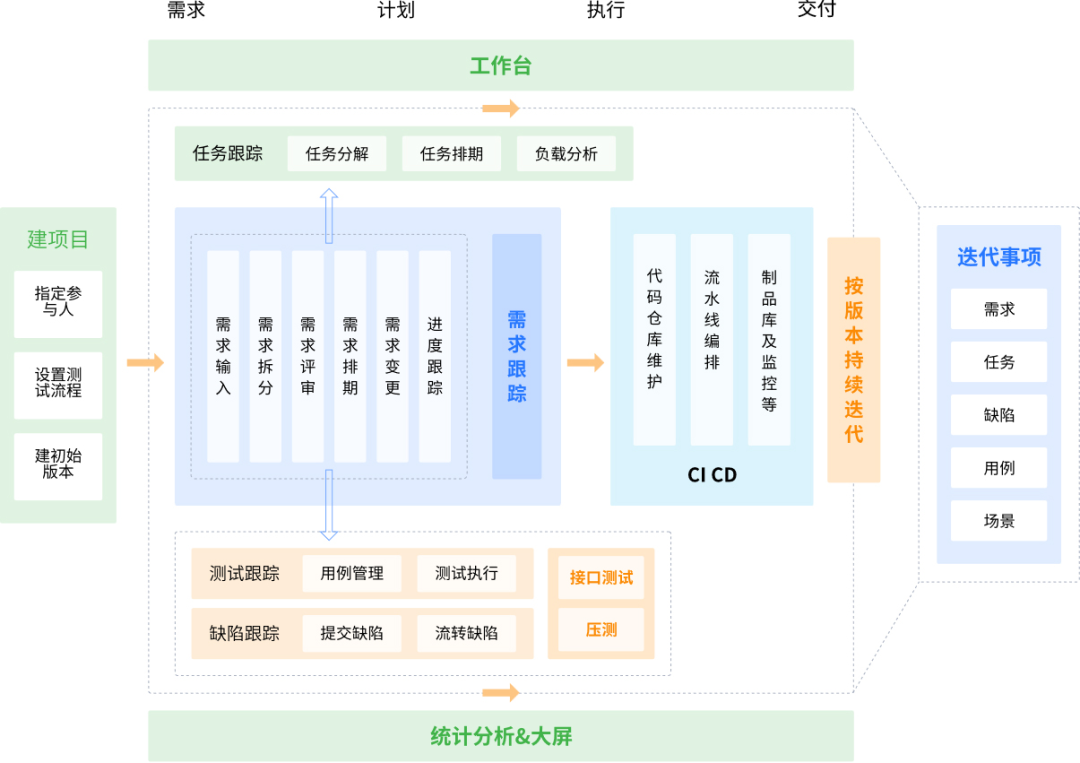
Codes 开源研发项目管理平台——敏捷测试管理创新解决方案
前言 Codes 是国内首款重新定义 SaaS 模式的开源项目管理平台,支持云端认证、本地部署、全部功能开放,并且对30人以下团队免费。它通过整合迭代、看板、度量和自动化等功能,简化测试协同工作,使敏捷测试更易于实施。并提供低成本的…...
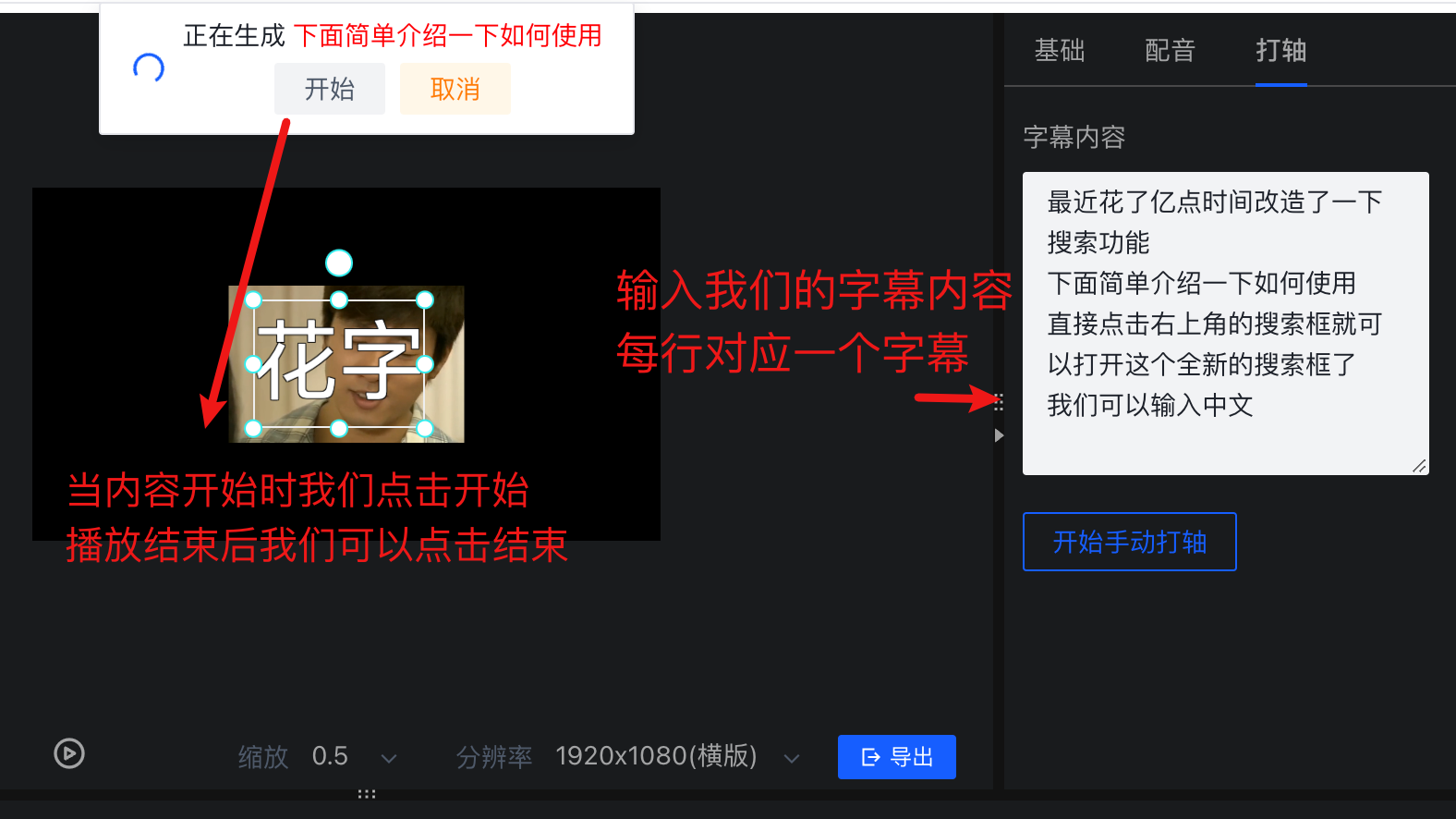
耗时一个月,我做了一个网页视频编辑器
最近又肝了一个多月,终于把这个网页视频编辑器做好了,下面我来简单介绍一下如何使用 注意目前该功能还处在测试阶段,可能会有很多问题,后续我会不断修复 体验地址 app.zyjj.cc 界面介绍 整个剪辑界面包括4个区,左边是…...

uniapp 做一个查看图片的组件,图片可缩放移动
因为是手机端,所以需要触摸可移动,双指放大缩小。 首先在components里建个组件 查看图片使用 uni-popup 弹窗 要注意 transform的translate和scale属性在同一标签上不会一起生效 移动就根据触摸效果进行偏移图片 缩放就根据双指距离的变大变小进行缩…...

卡车配置一键启动无钥匙进入手机控车
卡车智能一键启动无钥匙进入手机控车,通过手机应用程序与汽车内置硬件、软件的无线通信,实现对汽车的远程控制。 卡车改装一键启动的步骤包括安装门把手的感应装置、拆卸仪表台和门板,取出内部的待接线束,并将一键启动…...

计算机网络基础概念 交换机、路由器、网关、TBOX
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、VLAN是什么?二 、交换机三、路由器四、网关五、TBOX六、问题1 、网关和交换机的区别2、网关和路由器的区别 总结 前言 工作有感而发࿰…...

labview禁用8080端口
需求背景 最近电脑上安装了labview全家桶,发现idea的8080端口项目启动报错,一直提示8080端口被占用。最简单的办法就是找到8080端口的服务,然后关闭这个服务。但是我不想这么做,我想把labview的web服务器的端口给修改了。 操作教程 1、cmd查看8080端口 2、windows进程 同…...

字符串的KMP算法详解及C/C++代码实现
1. 原由 紧接上文,我们知道了暴力匹配的算法在时间运行上的缺陷,假设字符串T的长度为n,字符串P的长度为m,则整个算法的时间复杂度为O( n * m ),而对于一个复杂的现实情况而言 n >> m >> 2 (即…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
