Matplotlib - Statistical Distribution作图
1. 前言

在数据分析和统计学中,绘制统计分布图是非常重要的,因为它帮助我们直观地理解数据的特性,并为进一步的分析提供基础。统计分布图能够揭示数据集的结构、趋势、集中趋势和离散程度等信息,从而使我们更容易做出合理的假设、判断和决策。
2. hist直方图
适用于不同样本来源的比较,小数据集,不同样本间的数据分布比较
或同一来源数据集作图选择合适统计模型
直方图是一个常用的工具,用于展示单个变量的分布。它将数据按区间(bins)划分,并通过条形图展示每个区间内数据的频率或数量。
2.1 直方图的使用场景
1. 查看数据分布
直方图最常用的场景是查看数值型数据的分布情况。通过直方图可以直观了解数据是偏向于正态分布、偏态分布,还是存在多个峰值(多峰分布)
2. 选择合适的统计模型
通过直方图的形状,可以帮助确定数据是否适合某种统计模型。例如,判断数据是否符合正态分布、均匀分布或指数分布等。
3. 比较多个数据集的分布
直方图还可以用于比较多个数据集的分布。通过叠加或并排显示不同数据集的直方图,可以对比它们的分布差异
2.2 代码与图
import matplotlib.pyplot as plt
import numpy as np# 生成随机数据
data = np.random.randn(1000)# 绘制直方图
plt.hist(data, bins=30, alpha=0.7, color='b')# 添加标题和标签
plt.title('Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')# 显示图像
plt.show()

2.3 常见参数
| bins | 指定数据区间的数量 |
| alpha | 用于设置透明度,多个图形叠加时最好使用 |
| color | 用于设置柱形的颜色 |
| edgecolor | 设置图形元素的边缘颜色 |
| linewidth | 控制线条的宽度,单位为point |
3. boxplot箱形图
适用于同一样本来源,大小数据集皆可,内部不同时间/状况的样本比较
显示一组数据的分布情况和统计特征,特别是用于比较不同数据集的分布。它通过显示数据的 五个数值摘要(最小值、下四分位数、中位数、上四分位数、最大值),以及识别异常值,帮助我们快速了解数据的分布、离散程度、中心趋势等信息。
3.1 使用场景
1. 数据分布的可视化
同时展示多个数据集的分布情况(如不同实验组、不同变量的结果)。
适合用来查看数据的对称性、偏态以及是否存在异常值。
2. 数据的对比
可以通过比较多个箱线图,直观地对比不同组数据的中心趋势、变异性和分布
例如,比较两个班级的考试成绩分布、不同产品的销售额分布。
3. 检测异常值
快速发现数据中的异常值(outliers)。位于箱线图“胡须”之外的数据点即为异常值,帮助分析潜在的极端情况。
4. 查看数据的集中趋势和离散程度
直观地看到数据的中位数和四分位数,判断数据的集中趋势和离散程度。
适合用于非对称分布数据的可视化,例如工资分布、房价分布等。
3.2 异常点分析
是的,boxplot 中的异常值通常是指超出 1.5 倍四分位距(IQR, Interquartile Range)范围的数据点。具体来说,IQR 是上四分位数(Q3)和下四分位数(Q1)之间的距离,即:


1.5 倍的 IQR 是一个常用的标准,用于标识数据中的异常值。这个标准来源于统计学中对数据分布的一个经验法则。
3.3 代码与作图
import matplotlib.pyplot as plt
import numpy as np# 生成随机数据
np.random.seed(10)
data1 = np.random.normal(100, 10, 200)
data2 = np.random.normal(90, 20, 200)
data3 = np.random.normal(80, 15, 200)# 绘制箱线图
plt.boxplot([data1, data2, data3], patch_artist=True, widths=0.6, boxprops=dict(facecolor='lightblue'), medianprops=dict(color='red', linewidth=2), whiskerprops=dict(color='green'))# 添加标题
plt.title("Boxplot Example")
plt.xticks([1,2,3],['A','B','C']) #指定修改标签# 显示图形
plt.show()
3.4 相关参数
| vert | 设置箱线图的方向。True为垂直,False为水平 |
| patch_artist | 是否填充箱体,为True则填充 |
| showfliers | 是否显示异常值 |
| widths | 箱线图的宽度 |
| positions | 图所在的位置。position=[1,2,4] |
| boxprops | 控制箱体的样式,boxprops=dict(facecolor='',color='') |
| flierprops | 设置异常值的样式,传入字典 |
| showmeans | 是否显示数据的均值 |
4. errorbar误差条
适用于同一样本来源,小数据集,比较内部数据
误差条是用来展示每个数据的浮动误差,显示测量误差或者不确定性
4.1 使用场景
-
测量误差:当你有测量数据时,通常需要显示每个数据点的误差范围。error可以在数据点上添加误差条,帮助显示这些测量误差。
-
数据的不确定性:在科学实验或数据分析中,数据的准确性可能受到各种因素的影响,
errorbar可以帮助你表示这些不确定性。 -
比较数据:当你比较不同实验组或条件下的数据时,误差条可以帮助你更好地理解数据的变异性和可靠性。
4.2 代码与作图
#errorbar
x = [2,4,6]
y = [3,7,11]
yerr = [0.3,0.5,0.9]fig,ax = plt.subplots()
ax.errorbar(x,y,yerr,fmt='o',linewidth=3,capsize=10)

4.3 相关参数
| fmt | 设置数据点的标记样式 |
| ecolor | 设置误差线的颜色 |
| linewidth | 设置误差线的宽度 |
| capsize | 设置误差端点的长度 |
| xerr | x轴数据的误差 |
| yerr | y轴数据的误差 |
5. violinplot小提琴图
5.1 简介
同一样本或不同样本比较均可使用
Violin图是结合了箱线图和核密度线的图片,展示数据的分布情况。
核密度线(KDE):Violin的形状代表数据的分布密度。越宽表示该值附近的数据点多,窄就表示越少
两侧对称:左右分布是一样的,使图形更容易解读
5.2 代码与作图
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np# 生成随机数据
data = np.random.normal(size=100)# 使用 seaborn 绘制 violin 图
sns.violinplot(data=data)# 显示图形
plt.show()

6. pie饼状图
适用于同一样本来源,小数据集,内部种类比较
饼图适用于展示数据中各部分在整体中所占比例的场景。它能够直观地展示每个部分的相对大小,适合少量分类数据的可视化。
6.1 使用场景
1. 比例分析
当你想展示数据集中不同类别的占比,如市场份额、预算分配、人口构成等,饼图是很合适的选择。例如,展示公司不同产品线的销售额占比。
2. 数据种类较少
饼图通常只适用于少量分类数据(一般不超过 5-6 类)。如果分类过多,饼图会显得杂乱且难以阅读。
6.2 代码与作图
import matplotlib.pyplot as plt# 数据
sizes = [15, 30, 45, 10]
labels = ['Apples', 'Bananas', 'Cherries', 'Dates']
colors = ['gold', 'yellowgreen', 'lightcoral', 'lightskyblue']
explode = (0, 0.1, 0, 0) # 'Bananas' 部分稍微爆开# 绘制饼图
plt.pie(sizes, explode=explode, labels=labels, colors=colors,autopct='%1.1f%%', shadow=True, startangle=140)# 确保饼图为圆形
plt.axis('equal')# 添加标题
plt.title("Fruit Consumption Pie Chart")# 显示图形
plt.show()

6.3 相关参数
| labels | label=['A','B'],添加标签 |
| color | 自定义块的颜色 |
| autopct | 显示每个部分的百分比 |
| explode | explode=[0,0.1,0,0],设置每部分是否分离,分离的距离 |
| shadow | 添加阴影效果 |
| radius | 设置饼图的半径 |
| pctdistance | 设置百分比标签与饼图中心的距离 |
7. hist2d二维直方图
适用于大数据集,同一样本来源的内部数据分布比较
适用于将两个变量的分布情况在二维平面上进行可视化。该函数会根据传入的两个变量,将数据按网格进行划分,并统计每个网格中的数据点数,最终生成一个二维热图。
7.1 使用场景
1. 分析两个连续变量之间的关系
当你有两个连续变量并想观察它们之间的相关性或分布模式时,hist2d() 是很好的工具。它会把数据分成网格(bins),并显示每个网格内的数据点数量。
2. 大规模数据集
将数据分箱处理,把数据点密集的区域以颜色浓度来表示,能够更加清晰地显示数据分布。
3. 数据量大的情况下替代散点图
如果数据量过大,散点图的点可能会重叠,导致图形难以解释。hist2d() 可以通过统计数据点数量,以颜色的深浅来表示点的密集程度,能够更好地处理数据重叠的问题。
7.2 代码与作图
import matplotlib.pyplot as plt
import numpy as np# 生成一些随机数据
x = np.random.randn(10000) # 横轴数据
y = np.random.randn(10000) # 纵轴数据# 绘制二维直方图
plt.hist2d(x, y, bins=30, cmap='Blues')# 添加颜色栏
plt.colorbar(label='Counts')# 显示图形
plt.show()

7.3 相关参数
| bins | 设置每个维度上的箱子数,也决定了网格的分辨率,(3,4) |
| range | 定义二维直方图的范围 |
| cmap | 颜色映射,用于指定不同箱子计数的颜色,'Blues','Reds' |
| density | 返回的数据归一化,总面积为1 |
| cmin | 设定颜色强度的最小值,小于将被设置为透明 |
8. hexbin蜂窝图
适用于大数据集,同一样本来源的内部数据分布比较
8.1 简介
与hist2d效果相似,都用于可视化二维数据的分布情况
使用的是 六边形网格,将数据划分为蜂窝状的六边形区域。这使得视觉上更加紧凑,六边形网格在表示连续数据分布时可以减少“边界效应”,在某些情况下能比矩形网格更好地展示数据分布。
8.2 代码与作图
import numpy as np
import matplotlib.pyplot as plt# 生成随机数据
x = np.random.randn(10000)
y = np.random.randn(10000)# 绘制六边形分箱图
plt.hexbin(x, y, gridsize=30, cmap='Blues')
plt.colorbar(label='Counts')
plt.title('hexbin Example')
plt.show()

9. ecdf累计概率密度图
适用于小数据集,同一样本来源中数据大小分布比较
展示了数据集中每个数据点的值在整体数据中的累积百分比,即有多少比例的数据点小于等于某个值。
9.1 特点
-
1. 累积分布:ECDF 图展示的是每个数据点的值和它在整个数据集中的相对排名(累积百分比)。因此,纵轴(y 轴)表示的是累积概率,范围从 0 到 1,横轴(x 轴)是数据点的值。
-
2. 每个数据点对应一个累积概率:图中的每一个点表示一个数据点和它在数据集中所占的比例。例如,某个点的 y 值是 0.6,意味着 60% 的数据点小于或等于这个点的 x 值。
-
3. 对数据分布的完整描述:与直方图和密度图不同,ECDF 图展示了 每个数据点 的信息,避免了由于数据分箱导致的失真,因此它保留了数据的精确信息,适合小数据集。
9.2 代码与作图
a = np.random.normal(4,2,10)
print(a)
fig,ax = plt.subplots()
ax.ecdf(a)
相关文章:

Matplotlib - Statistical Distribution作图
1. 前言 在数据分析和统计学中,绘制统计分布图是非常重要的,因为它帮助我们直观地理解数据的特性,并为进一步的分析提供基础。统计分布图能够揭示数据集的结构、趋势、集中趋势和离散程度等信息,从而使我们更容易做出合理的假设、…...

【机器学习】9 ——最大熵模型的直观理解
系列文章目录 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前奏例子硬币垃圾邮件代码 前奏 【机器学习】6 ——最大熵模型 例子 硬币 假设我们有一枚硬币,可能是公平的,…...

1.单例模式
目录 简介 饿汉式 懒汉式 双重检测锁式 静态内部类式 枚举单例 测试 测试单例模式: 测试五种单例模式在多线程环境下的效率 问题(拓展) 例:反射破解单例模式 例:反序列化破解单例模式 总结:如何…...

数据倾斜问题
数据倾斜:主要就是在处理MR任务的时候,某个reduce的数据处理量比另外一些的reduce的数据量要大得多,其他reduce几乎不处理,这样的现象就是数据倾斜。 官方解释:数据倾斜指的是在数据处理过程中,由于某些键…...

大龄焦虑?老码农逆袭之路:拥抱大模型时代,焕发职业生涯新活力!
其实我很早就对大龄程序员这个话题感到焦虑,担心自己35岁之后会面临失业,有时和亲戚朋友聊天时,也会经常拿这个出来调侃。现在身边已经有很多35岁左右的同事,自己过两年也会步入35岁的行列,反倒多了一份淡定和从容。 …...

Vue 页面反复刷新常见问题及解决方案
Vue 页面反复刷新常见问题及解决方案 引言 Vue.js 是一个流行的前端框架,旨在通过其响应式的数据绑定和组件化的开发模式简化开发。然而,在开发 Vue.js 应用时,页面反复刷新的问题可能会对用户体验和开发效率产生负面影响。本文将深入探讨 …...
Windows上指定盘符-安装WSL虚拟机(机械硬盘)
参考来自于教程1:史上最全的WSL安装教程 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/386590591#%E4%B8%80%E3%80%81%E5%AE%89%E8%A3%85WSL2.0 教程2:Windows 10: 将 WSL Linux 实例安装到 D 盘,做成移动硬盘绿色版也不在话下 - 知乎 (z…...
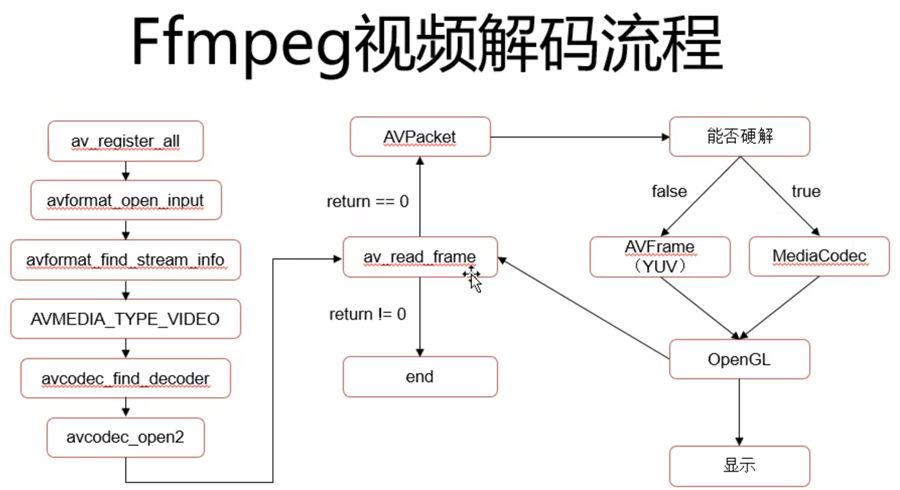
ffmpeg实现视频的合成与分割
视频合成与分割程序使用 作者开发了一款软件,可以实现对视频的合成和分割,界面如下: 播放时,可以选择多个视频源;在选中“保存视频”情况下,会将多个视频源合成一个视频。如果只取一个视频源中一段视频…...

团体标准的十大优势
一、团体标准是什么 团体标准是指由社会团体(行业协会、联合会、企业联盟等)按照自己确立的制定程序,自主制定、发布、采纳,并由社会自愿采用的标准。简单的说,就是社会团体为了满足市场和创新需要,协调相…...
任务、动态添加停止单个cron任务)
java spring boot 动态添加 cron(表达式)任务、动态添加停止单个cron任务
java spring boot 动态添加 cron(表达式)任务、动态添加停止单个cron任务 添加对应的maven <dependency><groupId>org.quartz-scheduler</groupId><artifactId>quartz</artifactId><version>2.3.0</version…...

sqlgun靶场漏洞挖掘
1.xss漏洞 搜索框输入以下代码,验证是否存在xss漏洞 <script>alert(1)</script> OK了,存在xss漏洞 2.SQL注入 经过测试,输入框存在SQL注入漏洞 查询数据库名 查询管理员账号密码 此处密码为MD5加密,解码内容如下 找…...

好用的 Markdown 编辑器组件
ByteMD bytedance/bytemd: ByteMD v1 repository (github.com) 这里由于我的项目是 Next,所以安装 bytemd/react, 阅读官方文档,执行命令来安装编辑器主体、以及 gfm(表格支持)插件、highlight 代码高亮插件…...

uniapp vite3 require导入commonJS 的js文件方法
vite3 导入commonJS 方式导出 在Vite 3中,你可以通过配置vite.config.js来实现导入CommonJS(CJS)风格的模块。Vite 默认支持ES模块导入,但如果你需要导入CJS模块,可以使用特定的插件,比如originjs/vite-pl…...
通义灵码用户说:“人工编写测试用例需要数十分钟,通义灵码以毫秒级的速度生成测试代码,且准确率和覆盖率都令人满意”
通过一篇文章,详细跟大家分享一下我在使用通义灵码过程中的感受。 一、定义 通义灵码,是一个智能编码助手,它基于通义大模型,提供代码智能生成、研发智能问答能力。 在体验过程中有任何问题均可点击下面的连接前往了解和学习。 …...

MySQL中的约束
约束概述 1.1 为什么需要约束 数据完整性(Data Integrity)是指数据的精确性(Accuracy)和可靠性(Reliability)。它是防止数据库中存在不符合语义规定的数据和防止因错误信息的输入输出造成无效操作或错误信…...

Leetcode 寻找重复数
可以使用 位运算 来解决这道题目。使用位运算的一个核心思想是基于数字的二进制表示,统计每一位上 1 的出现次数,并与期望的出现次数做比较。通过这种方法,可以推断出哪个数字重复。 class Solution { public:int findDuplicate(vector<i…...

大一新生以此篇开启你的算法之路
各位大一计算机萌新们,你们好,本篇博客会带领大家进行算法入门,给各位大一萌新答疑解惑。博客文章略长,可根据自己的需要观看,在博客中会有给大一萌新问题的解答,请不要错过。 入门简介: 算法…...

【AI大模型】ChatGPT模型原理介绍(上)
目录 🍔 什么是ChatGPT? 🍔 GPT-1介绍 2.1 GPT-1模型架构 2.2 GPT-1训练过程 2.2.1 无监督的预训练语言模型 2.2.2 有监督的下游任务fine-tunning 2.2.3 整体训练过程架构图 2.3 GPT-1数据集 2.4 GPT-1模型的特点 2.5 GPT-1模型总结…...

基于UE5和ROS2的激光雷达+深度RGBD相机小车的仿真指南(五):Blender锥桶建模
前言 本系列教程旨在使用UE5配置一个具备激光雷达深度摄像机的仿真小车,并使用通过跨平台的方式进行ROS2和UE5仿真的通讯,达到小车自主导航的目的。本教程默认有ROS2导航及其gazebo仿真相关方面基础,Nav2相关的学习教程可以参考本人的其他博…...

C++竞赛初阶L1-15-第六单元-多维数组(34~35课)557: T456507 图像旋转
题目内容 输入一个 n 行 m 列的黑白图像,将它顺时针旋转 90 度后输出。 输入格式 第一行包含两个整数 n 和 m,表示图像包含像素点的行数和列数。1≤n≤100,1≤m≤100。 接下来 n 行,每行 m 个整数,表示图像的每个像…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
