Games101图形学笔记——光栅化
这里写目录标题
- Rasterization光栅化
- 屏幕空间
- 隔行扫描
- 三角形
- 采样
- 采样产生的问题
- 反走样处理方法:采样前模糊
- 频率,时域
- 傅里叶级数展开
- 傅里叶变换
- 滤波
- 高通滤波
- 低通滤波
- 卷积
- 卷积的一些定理
- 反走样
- MSAA(Multisample Anti-Aliasing)多重采样抗锯齿
Rasterization光栅化
把三维空间的几何形体显示在屏幕上

在进行了上节课的操作之后,所有物体都处在了[-1,1]³的立方体中,接下来就要把他画在屏幕上,这一步就叫做光栅化
在做透视投影时候需要将一个四棱梯挤压成正方体,就需要先定义一个视锥(四棱锥)
如何定义视锥?

从摄像机看向一个地方,我们把它当作近平面,宽和高是可以定义的,所以宽高比就是可以定义的
- 宽高比 Aspect ratio
- 可视角度 FOV (垂直角度和水平角度可以互相转换)
通过以上两点即可定义一个视锥

要把图像投影到屏幕上就需要先定义屏幕,在图形学中,屏幕就认为是一个装了像素的二维数组。如数组大小1920*1080
像素是最小单位,每个像素由RBG构成
屏幕空间
屏幕坐标系如下图

像素的坐标以左下角为准,如图中蓝色像素坐标为(2,1)
像素的中心为(x+0.5,y+0.5)
继续上节课的话题
如何将[-1,1]³中的东西显示到屏幕上呢?

- 暂时忽略z
- 如果只将[-1,1]²中的东西显示到[0,width] x [0,height],那么就很简单了
做个缩放并平移就可以,这个变换就被称为视口变换

隔行扫描

以前的显示设备要成像,都是在屏幕上画很多线,画满整个屏幕就形成了一帧画面
隔行扫描就是说
在第一帧只画1、3、5等奇数线
在第二帧只画2、4、6等偶数线
利用人眼的视觉残留特性,这样人们即发现不了画面的异常,还能使机器工作量减半
如今还有某些视频压缩技术采用了这个思想
(但是隔行扫描会造成严重的画面撕裂,特别是对高速运动的画面来说)
三角形

- 为什么光栅化选择了三角形?
- 三角形是最基本的多边形,没有比三角形边更少的多边形 其他多边形都可以拆分为三角形 三角形必定在一个平面内
- 容易定义三角形的里外 三角形的三个点定义好后,三角形内任意一点可以通过线性的插值来计算得到(重心坐标的插值方法)
如:定义好三个点的颜色,三角形内任意一点的颜色可以通过三个点的颜色来进行插值计算得到
如何将三角形转化为一个一个的像素?

简单近似采样
给定一个连续的函数f(x),当x等于1时得到的f(1)就是1的采样
所以采样就是把一个函数离散化的过程
只要有一个定义在屏幕空间的函数,那么我们就能算出来不同像素中心的值是多少
我们要采样的东西就是
给定一个三角形,在像素的中心进行采样,来判断中心是否落在三角形内

逐像素遍历,判断该像素中心是否在三角形内部,输出到屏幕显示

但是遍历所有像素开销太大,如下图中白色那一列的像素根本没有碰到三角形,所以只要遍历蓝色区域就可以了
我们知道三角形三个顶点的坐标,有了Xmin,Ymin,Xmax,Ymax就可以得到蓝色的区域
蓝色区域就叫做包围盒(轴向包围盒/BoundingBox/AABB)

采样完成后,因为每个像素都是最小单位,像素内的颜色必须一样,所以我们会得到这样一副图

这看起来和初始的三角形差别很大,有一个个的明显锯齿(Jaggies/Aliasing)
采样
把到达光学元件上的光,产生的信息,离散成了像素,对这些像素采样,形成了照片
采样不只发生在位置上还能发生在时间上,对图像在时间上进行采样,形成了视频
采样产生的问题
- 走样
- 摩尔纹
- 车轮效应
原因就是信号的变化太快了,以至于采样的速度跟不上
反走样处理方法:采样前模糊

不能先采样再模糊!只能先模糊在采样
频率,时域
频域和时域是对信号或系统的两种不同的表示方式。
频域表示是通过分析信号的频率分布来表示信号的方式。在频域中,信号被分解为一系列不同频率的分量,每个分量对应着信号中的一种特定的周期性成分。
时域表示是通过直接分析信号在时间上的变化情况来表示信号的方式。在时域中,信号的变化被直接表示为在时间上的变化,而不是在频率上的变化。

傅里叶级数展开
任何一个周期性的函数都可以变成一系列正弦/余弦的线性组合和一个常数项

傅里叶变换
可以把一个函数f(x)通过变化变成F(w),F(w)还能通过逆变换变成f(x)

对五个不同频率的函数波形进行采样
通过f1(x)、f2(x)的采样点,我们可以大致还原出f1(x)\f2(x)的函数波形
但是从f3(x)开始,还原出的波形和原来的函数有较大出入,越往下越明显
这里就可以理解什么叫采样的频率跟不上信号变化的频率了

我们对蓝色函数进行采样,得到黑色的函数
但假如原本就有这样一个黑色的函数
我们同时对蓝色和黑色进行采样,两个截然不同的函数,得到的采样结果完全相同
这就被称为走样(Aliases)

滤波
滤波就是抹掉一些特定的频率
对应的信号如何发生变化
傅里叶变换可以把一个函数从时域变到频域
右边的图像就是左边的照片通过傅里叶变换得到的
右边图像表示的就是有多少信息
中间部分是低频信息,越往外越高频

高通滤波
在频域空间内完全抹掉低频信号,将结果还原成图像,形成左图
高频的东西在图像上表示的就是图像的边界
为什么高频信息代表着边界?
当某一图像的周围突然发生发生了变化,我们就认为他是边界
比如图中人物的衣服和背景就是由黑色突然变成了灰色
相当于颜色信号突然从黑色变成了灰色,就是出现了高频的变化,即边界

低通滤波
同理高通滤波,得到模糊的图像

去除高频和低频,只留一部分


卷积
移动窗口(Filter),将窗口中三个数和覆盖信号的三个数做点乘,填到结果中


其实就是信号在任意一个地方,在他的周围做了个平均操作
卷积的一些定理
时域的卷积 == 频域的乘积
- 可以拿到一幅图直接用一个卷积滤波器进行卷积操作
- 也可以
1. 先傅里叶变换这幅图,将这幅图变到频域
2. 将卷积滤波器变到频域上
3. 将两者相乘,乘完后得到的频域的结果,将其逆傅里叶变换,变到时域上

将3*3的滤波器乘1/9是为了不让图像整体的颜色发生变化
如果不乘1/9,那么每个像素就会是原来这个像素周围九个像素的和,图像就会越滤波越明亮了


左边一列是时域,右边一列是频域
对a图像进行c的采样,得到e
对应的操作在频域中就是bdf
时域的采样在频域中就就体现为频域信号的复制
(这里老师说左边时域进行乘积=右边频域的卷积,和前文说的不一致,我去查了一下,好像两种说法是相互的,都可以,这里不太懂,但是不影响整体的理解)
为什么会产生走样呢?
采样不同的间隔,会引起频谱不同间隔进行复制,所相交的部分就是走样

反走样
先对图像做模糊(把高频信息拿掉),再采样

把高频信息砍掉,砍掉虚线方块以外,在以原始采样频率进行采样
这样频域图像就不会发生混叠,也就没有走样了

对覆盖面积求平均,也就是卷积

MSAA(Multisample Anti-Aliasing)多重采样抗锯齿
通过更多的样本来近似三角形的覆盖率,并不是提高采样频率
把一个像素划分为几个小点,判断这些小点是否在三角形内,再把结果平均起来,就知道三角形覆盖了这个像素的百分之多少



并不是简单的提高了采样的频率,只是用来做第一步模糊,求三角形的覆盖率,平均之后是什么
MSAA解决的其实是对信号的模糊操作
在工业界并不是直接将每个像素平均分了四份,而是采用了一些独特的图形,而且一些边缘的像素还会被复用


相关文章:

Games101图形学笔记——光栅化
这里写目录标题 Rasterization光栅化屏幕空间隔行扫描三角形采样采样产生的问题反走样处理方法:采样前模糊 频率,时域傅里叶级数展开傅里叶变换 滤波高通滤波低通滤波 卷积卷积的一些定理 反走样MSAA(Multisample Anti-Aliasing)多…...

2024年汉字小达人区级自由报名的几个最新问题和真题练一练
2024年第十一届汉字小达人的区级活动的时间9月25-30日正式开赛,还有不到两周。 今天继续回答家长和孩子们的几个问题,并给大家看看一些真题,让孩子对汉字小达人的题型和比赛有直观的了解,从而更好地备考。 本专题在比赛前持续更…...

从简单分析到智能问数,Smartbi AIChat让数据回归业务
大数据产业创新服务媒体 ——聚焦数据 改变商业 在某科技公司,资深数据分析师李晨(化名)正忙于分析新产品的市场表现。面对传统自助式BI工具,李晨在功能界面中手动设置各种查询条件,进行了一番复杂的拖拉拽操作&#…...
基于SpringBoot+Vue+MySQL的考编论坛网站
系统展示 用户前台界面 管理员后台界面 系统背景 在当前信息化高速发展的时代,考编已成为众多求职者的重要选择。然而,备考过程中信息获取、经验交流及资源分享的需求日益凸显。基于SpringBoot、Vue.js与MySQL构建的考编论坛网站应运而生,旨在…...
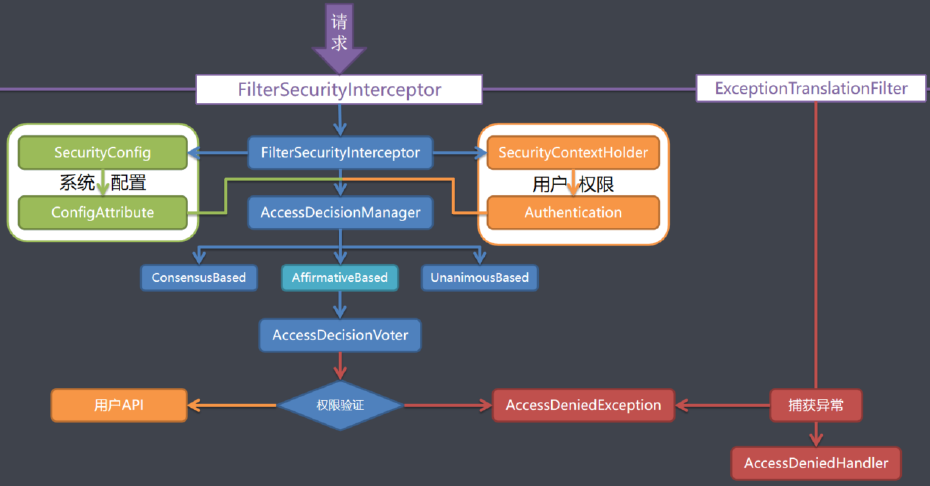
SpringSecurity剖析
1、SpringSecurity 入门 1.1、简介 Spring Security是一个功能强大且高度可定制的身份验证和访问控制框架。它是用于保护基于Spring的应用程序的实际标准。Spring Security是一个框架,致力于为Java应用程序提供身份验证和授权。与所有Spring项目一样,Sp…...

一文搞懂 Flink Graph 构建过程源码
一文搞懂 Flink Graph 构建过程 1. StreamGraph构建过程1.1 transform(): 构建的核心1.2 transformOneInputTransform1.3 构造顶点1.4 构造边1.5 transformSource1.6 transformPartition1.7 transformSink 1. StreamGraph构建过程 链接: 一文搞懂 Flink 其他重要源码点击我 e…...
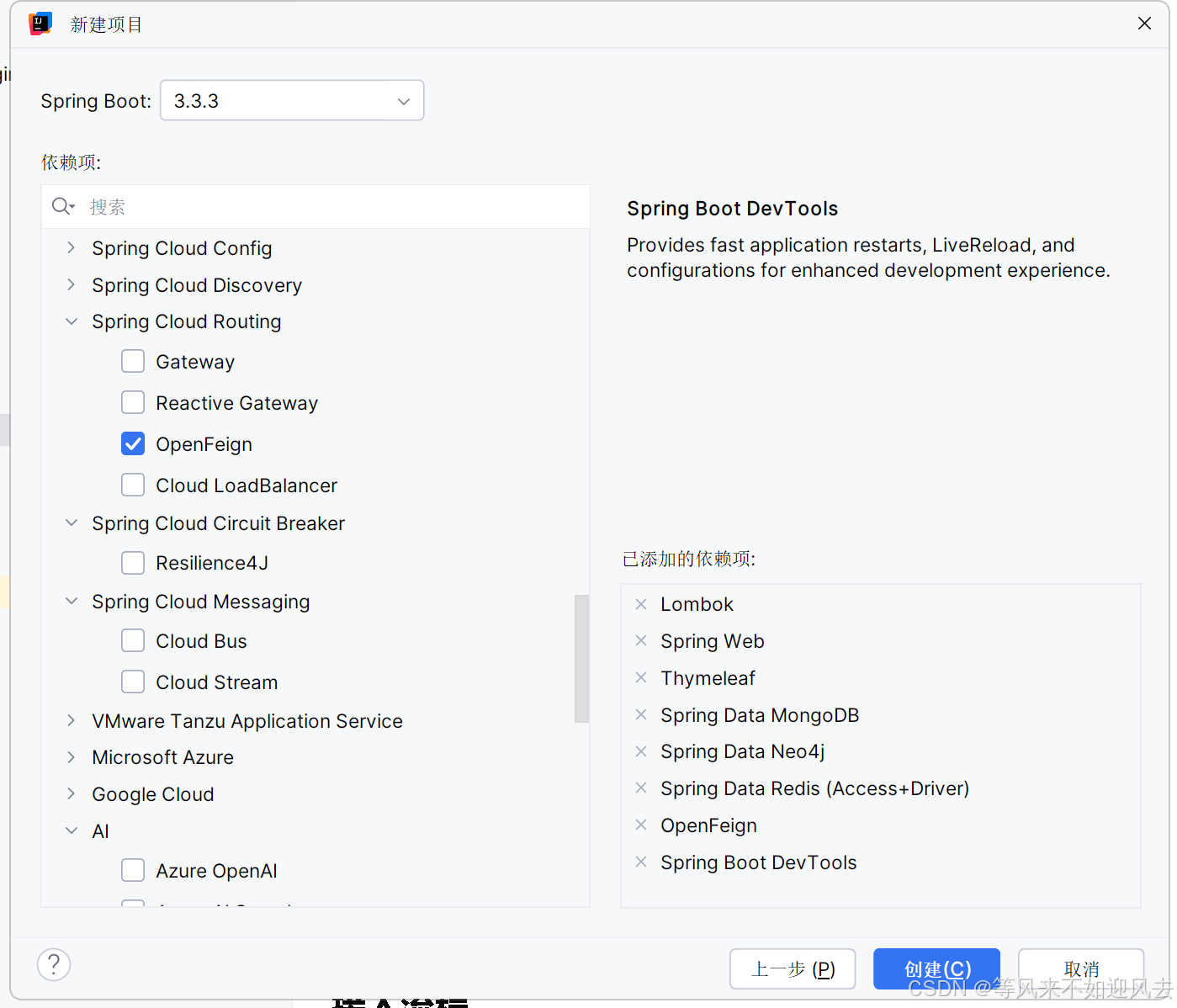
【spring】IDEA 新建一个spring boot 项目
参考新建项目-sprintboot 选择版本、依赖,我选了一堆 maven会重新下载一次么?...

LeetCode[简单] 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 思路:类似与二分查找 唯一需要注意的是,搜索…...
Bootstrap框架的HTML示例)
(代码可运行)Bootstrap框架的HTML示例
Bootstrap:一套流行的前端开发框架,基于HTML、CSS和JavaScript,适用于快速构建响应式Web应用。 以下是一个使用Bootstrap构建的简单响应式Web应用的HTML示例: <!DOCTYPE html> <html lang"en"> <head&…...

IntelliJ IDEA 2024创建Java项目
一、前言 本文将带领大家手把手创建纯Java项目,不涉及Maven。如有问题,欢迎大家在评论区指正说明! 二、环境准备 名称版本jdk1.8idea2024 1.4操作系统win10 jdk的安装教程 idea的安装教程 三、创建项目 首先我们点击新建项目 然后我们…...

Python之 条件与循环(Python‘s Conditions and loops)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:Linux运维老纪的首页…...

C++学习,多态纯虚函数
多态字面意思是多种形态,当类之间存在层次结构,并且类之间是通过继承时,就会用到多态。多态允许通过基类指针或引用来调用派生类中的成员函数。这种机制允许函数,在运行时根据对象的实际类型来确定执行哪个函数,从而实…...

飞速(FS)与西门子联合打造交换机自动化灌装测试生产线
2024年9月,备受信赖的信息通信技术(ICT)解决方案提供商飞速(FS)与工业自动化领域的领先企业西门子公司正式宣布,双方共同打造的ILTP(智能灌装测试平台)和自动化生产线将正式启动。此…...

Vue组合式API:setup()函数
1、什么是组合式API Vue 3.0 中新增了组合式 API 的功能,它是一组附加的、基于函数的 API,可以更加灵活地组织组件代码。通过组合式 API 可以使用函数而不是声明选项的方式来编写 Vue 组件。因此,使用组合式 API 可以将组件代码编写为多个函…...

Redis底层数据结构(详细篇)
Redis底层数据结构 一、常见数据结构的底层数据结构1、动态字符串SDS(Simple Dynamic String)组成 2、IntSet组成如何保证动态如何确保有序呢? 底层如何查找的呢? 3、Dict(dictionary)3.1组成3.2 扩容3.3 收缩3.4 rehash 4、ZipList连锁更新问题总结特…...

树和二叉树基本术语、性质
总结二叉树的度、树高、结点数等属性之间的关系(通过王道书 5.2.3 课后小题来复习“二叉 树的性质”) 树的相关知识 叶子结点的度0 层次默认从1开始 有些题目从0 开始也不要奇怪 常见考点1:结点数总度数+1 常见考点2࿱…...

FEDERATED引擎
入门 MySQL引擎主要有以下几种: MyISAM:这是MySQL 5.5.5之前的默认存储引擎,不支持事务、外键约束和聚簇索引,适用于读多写少的场景。InnoDB:这是MySQL 5.5.5之后的默认存储引擎,支持事务、外键约束、行级…...

Android NDK工具
Android NDK工具 Android NDK Crash 日志抓取及定位 NDK-STACK 定位 NDK Crash 位置 只要执行如下代码就行: adb logcat | ndk-stack -sym /yourProjectPath/obj/local/armeabi-v7aPS: 必须是带symbols的so,也就是在’\app\src\main\obj\local\下面的…...

使用 Docker 进入容器并运行命令的详细指南
Docker 是一款开源的容器化平台,它可以将应用程序和依赖环境打包到一个可移植的“容器”中,以保证应用不受运行环境的影响。使用 Docker 容器化应用后,有时需要进入容器内部执行一些命令进行调试或管理。 一、Docker 基础命令 在开始进入容…...

【人工智能】OpenAI最新发布的o1-preview模型,和GPT-4o到底哪个更强?最新分析结果就在这里!
在人工智能的快速发展中,OpenAI的每一次新模型发布都引发了广泛的关注与讨论。2023年9月13日,OpenAI正式推出了名为o1的新模型,这一模型不仅是其系列“推理”模型中的首个代表,更是朝着类人人工智能迈进的重要一步。本文将综合分析…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
