【蓝桥杯真题】包子凑数(裴蜀定理、动态规划、背包问题)
题意
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入与数据范围
第一行包含一个整数NNN。(1<=N<=100)(1 <= N <= 100)(1<=N<=100)
以下NNN行每行包含一个整数AiAiAi。(1<=Ai<=100)(1 <= Ai <= 100)(1<=Ai<=100)
算法(裴蜀定理,背包问题)
先给出两个数xxx,yyy是否能凑出最大数的问题。
- 如果xxx和yyy的最大公约数是1,那么它们存在不能够凑出的最大数,并且它们不能凑出的最大数是:(x−1)×(y−1)−1(x - 1) \times (y - 1) - 1(x−1)×(y−1)−1
- 在本题中,不能够凑出最大数意味着:他们不能凑出的数是有限的,因为不能够凑出的最大数为upupup,等价着大于upupup的所有数都能够被凑出,那么不能够凑出的数只可能在区间[1,up][1, up][1,up]中,显然,这个区间中的数是有限的。
所以我们先把所有蒸笼所装的包子数的最大公约数ddd给算出来。
// 最大公约数代码
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}
如果ddd不等于1,那么他们不存在不能够凑出的最大数,等价于不能够凑出的包子数量为无限个INF(infinity)。
否则我们就用动态规划来解决ddd等于1的情况,其实这种情况很简单。我们大致估计一下最大的不能够被凑出的包子数量的量级为:(100−1)×(100−1)−1(100 - 1) \times (100 - 1) - 1(100−1)×(100−1)−1,即为100001000010000量级。
我们定义状态数组:boolf[110][10010]bool \enspace f[110][10010]boolf[110][10010]
其中f[i][j]f[i][j]f[i][j]表示这A1∼AiA1 \sim AiA1∼Ai这些iii个蒸笼是否能够凑出数量为jjj的包子。
起初f[0][0]=truef[0][0] = truef[0][0]=true表示着000个包子可以被凑出,因为我们不需要选择任何蒸笼就已经凑出000个包子。
状态计算:f[i][j]=f[i−1][j]f[i][j] = f[i - 1][j]f[i][j]=f[i−1][j] 和 f[i][j]=f[i][j−a[i]](j>=a[i])f[i][j] = f[i][j - a[i]] \enspace (j >= a[i])f[i][j]=f[i][j−a[i]](j>=a[i])
AC代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, M = N * N;int n;
int a[N];
bool f[N][M];int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}int main() {cin >> n;for (int i = 1; i <= n; i ++) cin >> a[i];int d = 0;for (int i = 1; i <= n; i ++) d = gcd(d, a[i]);if(d != 1) cout << "INF" << "\n";else {f[0][0] = true;for (int i = 1; i <= n; i ++ ) {for (int j = 0; j < M; j ++) {f[i][j] = f[i - 1][j];if(j >= a[i]) {f[i][j] |= f[i][j - a[i]];}}}int res = 0;for (int i = 0; i < M; i ++)if(!f[n][i]) res ++ ;cout << res << "\n";}return 0;
}
相关文章:
)
【蓝桥杯真题】包子凑数(裴蜀定理、动态规划、背包问题)
题意 小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干…...

一种免费将PDF转word的方式
pdf转word的需求对我来说很重要,我经常会有PDF转word的方式,但是网上搜索到的方式,要么收费、要么限制pdf大小或者限制转换次数。这里我分享一种免费转换的方式:用Acrobat Pro 来做转换。Adobe Acrobat Pro拥有强大的功能…...
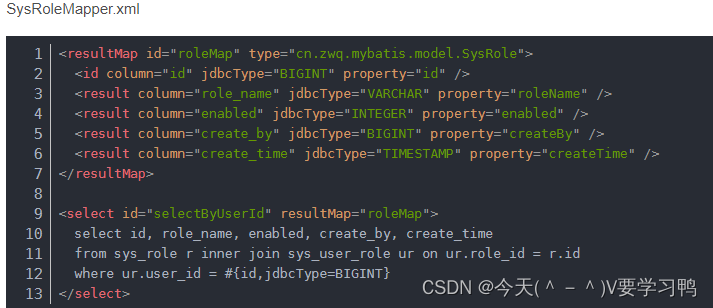
MyBatis-面试题
文章目录1.什么是MyBatis?2.#{}和${}的区别是什么?3.MyBatis的一级、二级缓存4.MyBatis的优缺点5.当实体类中的属性名和表中的字段名不一样 ,怎么办 ?6.模糊查询like语句该怎么写?7.Mybatis是如何进行分页的?分页插件的原理是什…...
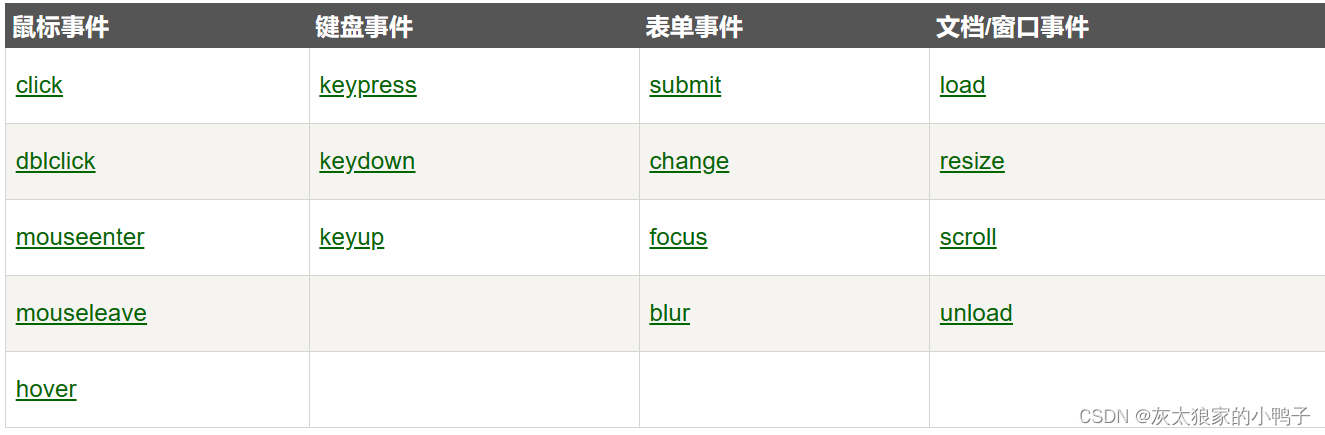
jQuery一些问题和ajax操作
jQuery语法: 文档就绪事件:文档加载之后运行jQuery代码,相当于jQuery的入口函数。 $(document).ready(function(){// 开始写 jQuery 代码...}); 简写: $(function(){// 开始写 jQuery 代码...}); jQuery选择器: …...

Pytorch构建自己的数据集
1.Pytorch内置的Dataset Pytorch中内置了许多数据集,我们可以从torchvision库中进行导入。比如,我们可以导入Fashion-MNIST数据集 import torch from torch.utils.data import Dataset from torchvision import datasets from torchvision.transforms …...
)
信息论小课堂:纠错码(海明码在信息传输编码时,通过巧妙的信道编码保证有了错误能够自动纠错。)
文章目录 引言I 纠错1.1 信息纠错的前提:信息冗余1.2 发现抄写错误的方法1.3 计算机的信息校验原理:奇偶校验1.4 有效的纠错编码II 案例2.1 例子1:自身DNA的编码2.2 例子2:海明码引言 预则立,不预则废:不确定性是我们这个世界自然的属性,在解决问题之前,要考虑到世界的不…...

MySQL执行计划(explain)
MySQL执行计划(explain) 1.什么是执行计划 2.如何分析执行计划 执行计划一共有12列,每一列都有着特殊的含义,接下来我们逐一分析 id select语句的查询顺序,包含一组数字,如果数字相同则从上到下,如果数字不同则从大到小。 select_type …...

思必驰回复第二轮审核问询,如何与科大讯飞、阿里巴巴“虎口夺食”?
数据智能产业创新服务媒体——聚焦数智 改变商业3月21日,思必驰科技股份有限公司(以下简称“思必驰”)更新上市申请审核动态,已回复上交所第二轮审核问询函,回复了涵盖关于实际控制人的认定、关于预计持续亏损及关于…...

基于Spring、SpringMVC、MyBatis的汽车租赁系统设计
文章目录 项目介绍主要功能截图:前台首页汽车信息列表汽车租赁留言反馈个人信息管理后台汽车类型管理汽车信息管理租赁信息管理用户管理续租信息管理归还信息管理保险信息管理违章登记管理部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创…...

读《刻意练习》后感,与原文好句摘抄
第一章,有目的的练习 所谓“天真的练习”,基本上只是反复的做某件事情,并指望只靠这种反复的练习,就能够提高表现和水平。 有目的练习的四个特点 有目的的练习具有定义明确的特定目标有目的的练习是专注的有目的的练习包含反馈…...

华为OD机试用java实现 -【选座位】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:选座位 题目 疫情期间需要大…...

国产蓝牙耳机怎么挑选?口碑最好的国产蓝牙耳机
蓝牙耳机已经成为现代人生活中必不可少的设备之一,因此市场上涌现出了众多的品牌和型号。但是,在这个竞争激烈的市场中,哪些品牌的蓝牙耳机更受欢迎呢?以下是几款口碑不错的蓝牙耳机品牌。 一、南卡小音舱蓝牙耳机 推荐系数&…...
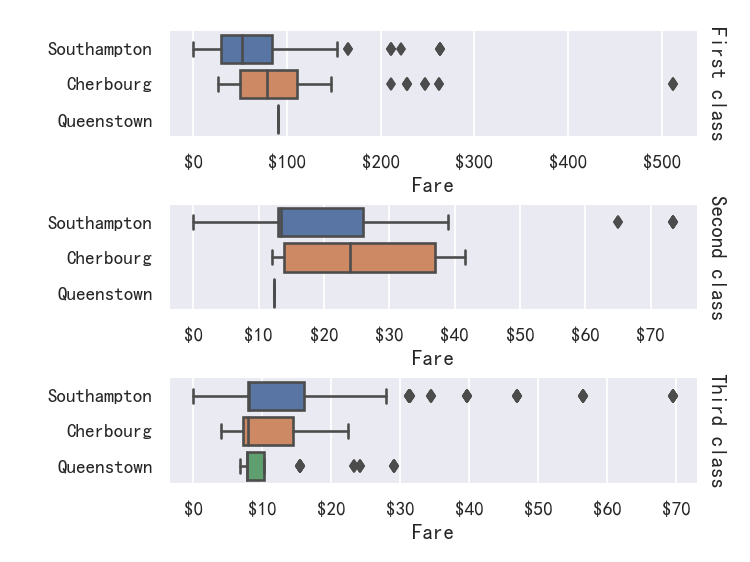
seaborn从入门到精通03-绘图功能实现02-分类绘图Categorical plots
seaborn从入门到精通03-绘图功能实现02-分类绘图Categorical plots总结参考关系-分布-分类分类绘图-Visualizing categorical data图形级接口catplot--figure-level interface导入库与查看tips和diamonds 数据分类散点图参考分布散点图stripplot分布密度散点图-swarmplot&#…...

❤️独特的算法❤️:一文解决编辑距离问题
编辑距离问题 题目关键点115. 不同的子序列 - 力扣(LeetCode)*dp数组定义,情况讨论583. 两个字符串的删除操作 - 力扣(LeetCode)两个字符串删除,情况讨论多加一种72. 编辑距离 - 力扣(LeetCode…...

三次样条样条:Bézier样条和Hermite样条
总结 What is the Difference Between Natural Cubic Spline, Hermite Spline, Bzier Spline and B-spline? 1.多项式拟合中的 Runge Phenomenon 找到一条通过N1个点的多项式曲线 ,需要N次曲线。通过两个点的多项式曲线为一次,三个点的多项式曲线为二…...
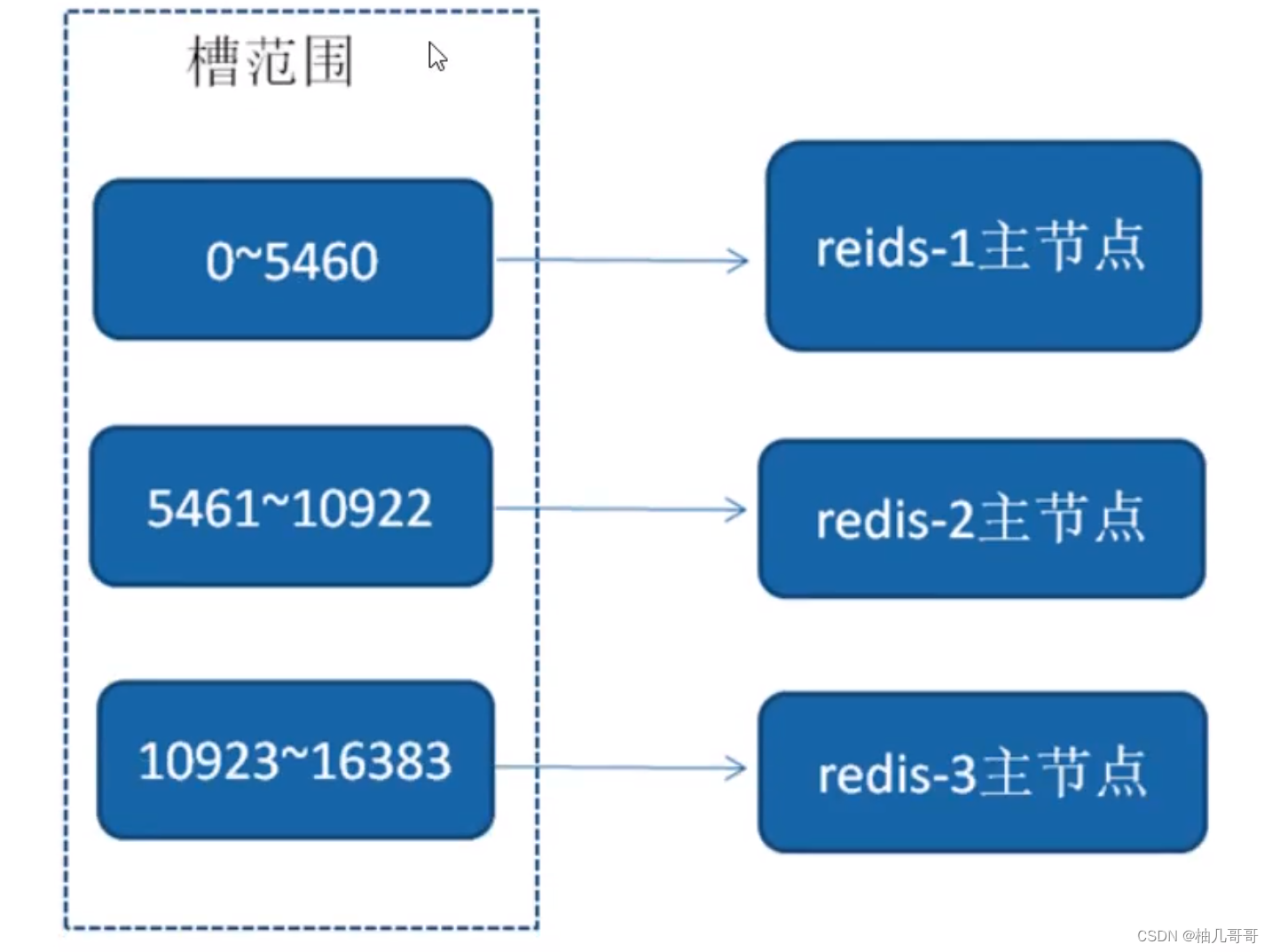
Redis面试题 (2023最新版)
文章目录一、Redis为什么快?1、纯内存访问2、单线程,避免上下文切换3、渐进式ReHash、缓存时间戳(1)渐进式ReHash:(2)缓存时间戳:二、Redis合适的应用场景常用基本数据类型ÿ…...

基于springboot实现家乡特色食品景点推荐系统【源码+论文】分享
基于springboot实现家乡特色推荐系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&…...
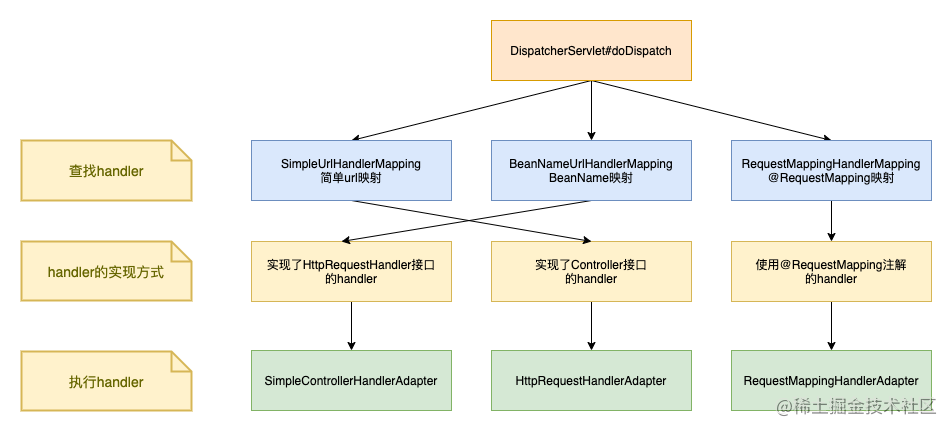
Spring MVC 启动之 HandlerMapping
在上一篇文章中,我们介绍了 Spring MVC 的启动流程,接下来我们将发分多个篇章详细介绍流程中的重点步骤 今天我们从 HandlerMapping 开始分析,HandlerMapping 是框架中的一个非常重要的组件。它的作用是将URL请求映射到合适的处理程序&#x…...

基于YOLOv5的停车位检测系统(清新UI+深度学习+训练数据集)
摘要:基于YOLOv5的停车位检测系统用于露天停车场车位检测,应用深度学习技术检测停车位是否占用,以辅助停车场对车位进行智能化管理。在介绍算法原理的同时,给出Python的实现代码、训练数据集以及PyQt的UI界面。博文提供了完整的Py…...

【Linux系统编程】5.vim基本操作命令
目录 跳转到指定行 命令模式 末行模式 跳转行首 跳转行尾 自动格式化代码 大括号、中括号、小括号对应 光标移至行首 光标移至行尾 删除单个字符 删除一个单词 删除光标至行尾 删除光标至行首 替换单个字符 删除指定区域 删除指定1行 删除指定多行 复制一行 …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
