代码随想录算法训练营第五十八天 | 拓扑排序精讲-软件构建

目录

软件构建

思路

拓扑排序的背景

拓扑排序的思路

模拟过程

判断有环

写代码

方法一： 拓扑排序

---

软件构建

• 题目链接：卡码网：117. 软件构建

• 文章讲解：代码随想录 

某个大型软件项目的构建系统拥有 N 个文件，文件编号从 0 到 N - 1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件 A 依赖于文件 B，则必须在处理文件 A 之前处理文件 B （0 <= A, B <= N - 1）。请编写一个算法，用于确定文件处理的顺序。

输入描述：

第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。

后续 M 行，每行两个正整数 S 和 T，表示 T 文件依赖于 S 文件。

输出描述：

输出共一行，如果能处理成功，则输出文件顺序，用空格隔开。

如果不能成功处理（相互依赖），则输出 -1。

输入示例：

5 4
0 1
0 2
1 3
2 4

输出示例：

0 1 2 3 4

提示信息：

文件依赖关系如下：

​

所以，文件处理的顺序除了示例中的顺序，还存在

0 2 4 1 3

0 2 1 3 4

等等合法的顺序。

数据范围：

• 0 <= N <= 10 ^ 5
• 1 <= M <= 10 ^ 9

思路

拓扑排序的背景

本题是拓扑排序的经典题目。

一聊到 拓扑排序，一些录友可能会想这是排序，不会想到这是图论算法。

其实拓扑排序是经典的图论问题。

先说说 拓扑排序的应用场景。

大学排课，例如 先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。

拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现 复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。

如果给出一条线性的依赖顺序来下载这些文件呢？

有录友想上面的例子都很简单啊，我一眼能给排序出来。

那如果上面的依赖关系是一百对呢，一千对甚至上万个依赖关系，这些依赖关系中可能还有循环依赖，你如何发现循环依赖呢，又如果排出线性顺序呢。

所以 拓扑排序就是专门解决这类问题的。

概括来说，给出一个 有向图，把这个有向图转成线性的排序 就叫拓扑排序。

当然拓扑排序也要检测这个有向图 是否有环，即存在循环依赖的情况，因为这种情况是不能做线性排序的。

所以拓扑排序也是图论中判断有向无环图的常用方法。

拓扑排序的思路

拓扑排序指的是一种 解决问题的大体思路， 而具体算法，可能是广搜也可能是深搜。

大家可能发现 各式各样的解法，纠结哪个是拓扑排序？

其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。

实现拓扑排序的算法有两种：卡恩算法（BFS）和DFS

卡恩1962年提出这种解决拓扑排序的思路

一般来说我们只需要掌握 BFS （广度优先搜索）就可以了，清晰易懂，如果还想多了解一些，可以再去学一下 DFS 的思路，但 DFS 不是本篇重点。

接下来我们来讲解BFS的实现思路。

以题目中示例为例如图：

​

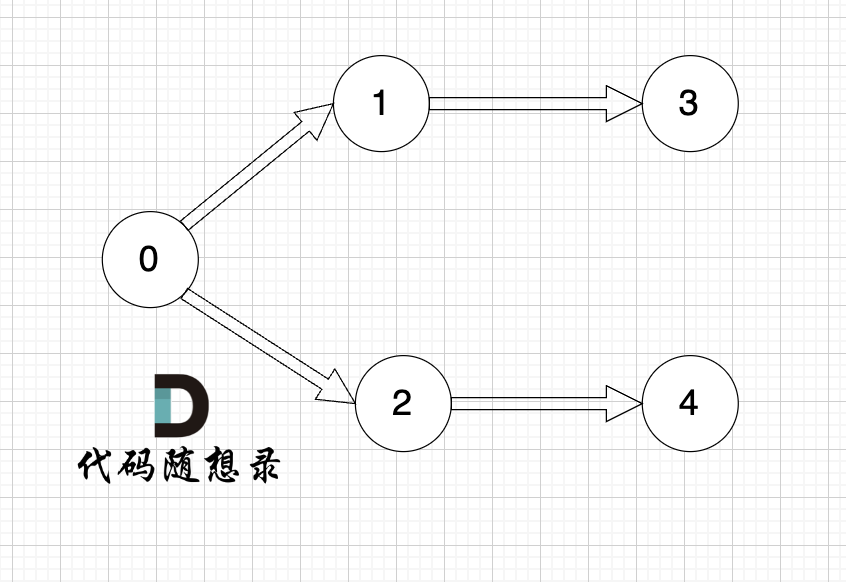
做拓扑排序的话，如果肉眼去找开头的节点，一定能找到 节点0 吧，都知道要从节点0 开始。

但为什么我们能找到 节点0呢，因为我们肉眼看着 这个图就是从 节点0出发的。

作为出发节点，它有什么特征？

你看节点0 的入度 为0 出度为2， 也就是 没有边指向它，而它有两条边是指出去的。

节点的入度表示 有多少条边指向它，节点的出度表示有多少条边 从该节点出发。

所以当我们做拓扑排序的时候，应该优先找 入度为 0 的节点，只有入度为0，它才是出发节点。 理解以上内容很重要！

接下来我给出 拓扑排序的过程，其实就两步：

1. 找到入度为0 的节点，加入结果集
2. 将该节点从图中移除

循环以上两步，直到 所有节点都在图中被移除了。

结果集的顺序，就是我们想要的拓扑排序顺序 （结果集里顺序可能不唯一）

模拟过程

用本题的示例来模拟这一过程：

1、找到入度为0 的节点，加入结果集

​

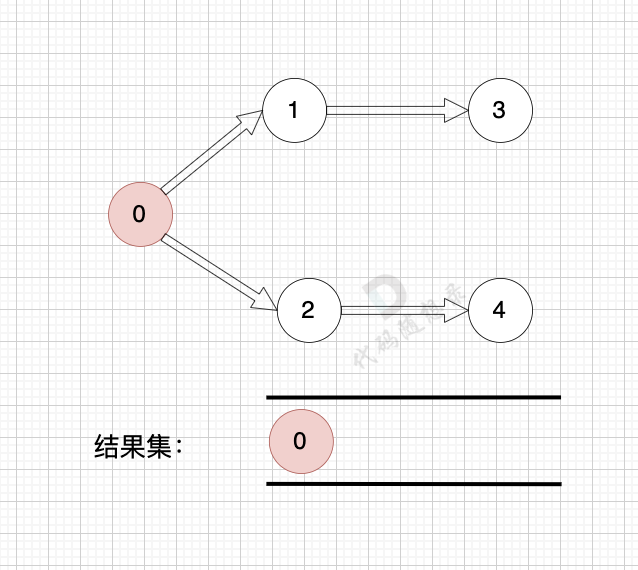
2、将该节点从图中移除

​

---

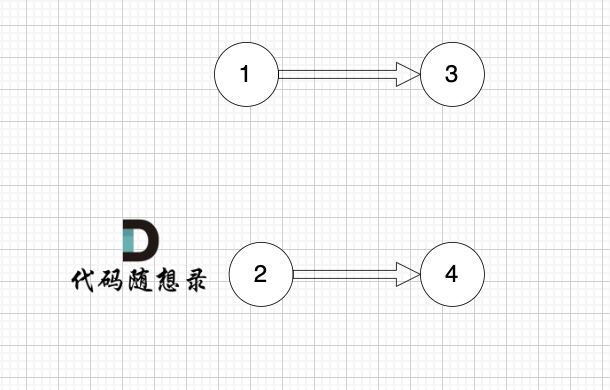
1、找到入度为0 的节点，加入结果集

​

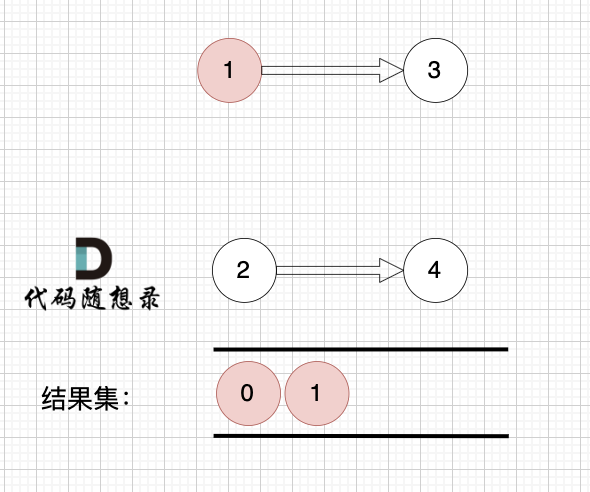
这里大家会发现，节点1 和 节点2 入度都为0， 选哪个呢？

选哪个都行，所以这也是为什么拓扑排序的结果是不唯一的。

2、将该节点从图中移除

​

---

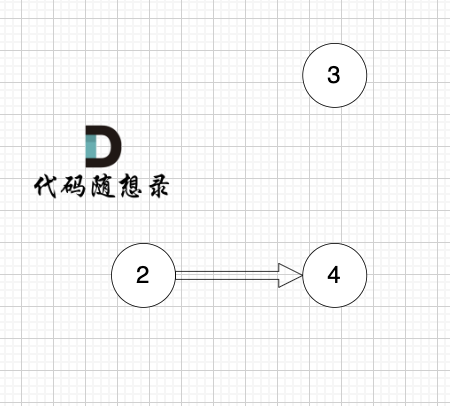
1、找到入度为0 的节点，加入结果集

​

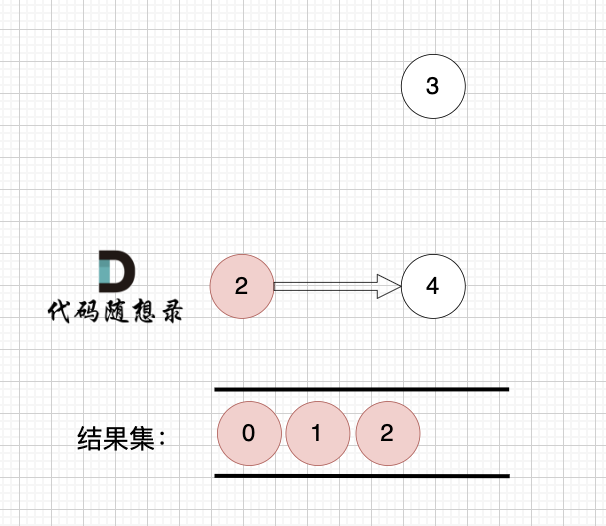
节点2 和 节点3 入度都为0，选哪个都行，这里选节点2

2、将该节点从图中移除

​

---

后面的过程一样的，节点3 和 节点4，入度都为0，选哪个都行。

最后结果集为： 0 1 2 3 4 。当然结果不唯一的。

判断有环

如果有 有向环怎么办呢？例如这个图：

​

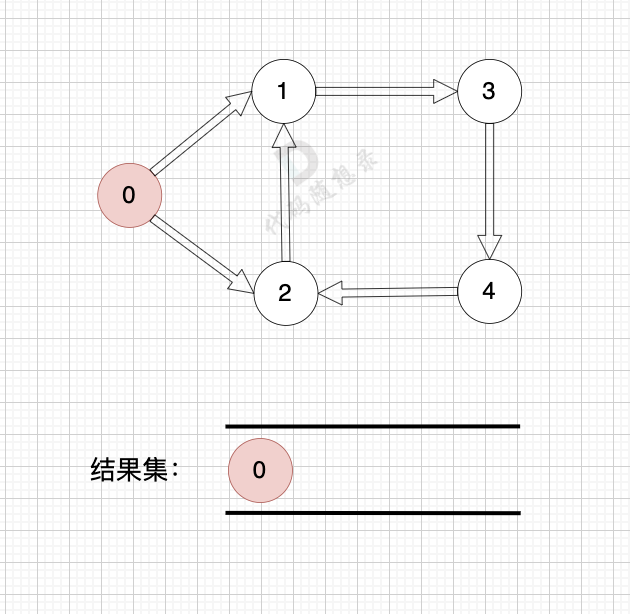
这个图，我们只能将入度为0 的节点0 接入结果集。

之后，节点1、2、3、4 形成了环，找不到入度为0 的节点了，所以此时结果集里只有一个元素。

那么如果我们发现结果集元素个数 不等于 图中节点个数，我们就可以认定图中一定有 有向环！

这也是拓扑排序判断有向环的方法。

通过以上过程的模拟大家会发现这个拓扑排序好像不难，还有点简单。

写代码

理解思想后，确实不难，但代码写起来也不容易。

为了每次可以找到所有节点的入度信息，我们要在初始化的时候，就把每个节点的入度 和 每个节点的依赖关系做统计。

代码如下：

# 记录每个文件的入度
inDegree = [0] * n
# 记录文件的依赖关系
ucamp = defaultdict(list)# s->t，先有s才能有t
for s,t in edges:#t的入度加一inDegree[t] += 1# 记录s指向哪些文件ucamp[s].append(t)

找入度为0 的节点，我们需要用一个队列放存放。

因为每次寻找入度为0的节点，不一定只有一个节点，可能很多节点入度都为0，所以要将这些入度为0的节点放到队列里，依次去处理。

代码如下：

# 初始化队列，加入入度为0的节点
que = deque([i for i in range(len(inDegree)) if inDegree[i] == 0])

 开始从队列里遍历入度为0 的节点，将其放入结果集。

while que:# 当前选中的文件cur = que.popleft()result.append(cur)

 这里面还有一个很重要的过程，如何把这个入度为0的节点从图中移除呢？

首先我们为什么要把节点从图中移除？

为的是将 该节点作为出发点所连接的边删掉。

删掉的目的是什么呢？

要把 该节点作为出发点所连接的节点的 入度 减一。

如果这里不理解，看上面的模拟过程第一步：

​

这事节点1 和 节点2 的入度为 1。

将节点0删除后，图为这样：

​

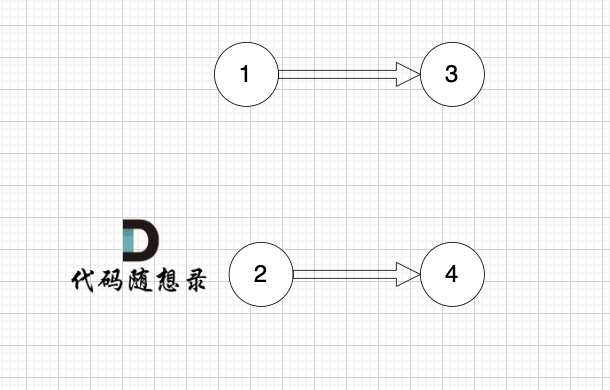
那么 节点0 作为出发点 所连接的节点的入度 就都做了 减一 的操作。

此时 节点1 和 节点 2 的入度都为0， 这样才能作为下一轮选取的节点。

所以，我们在代码实现的过程中，本质是要将 该节点作为出发点所连接的节点的 入度 减一 就可以了，这样好能根据入度找下一个节点，不用真在图里把这个节点删掉。

方法一： 拓扑排序

from collections import deque, defaultdictdef topological_sort(n, edges):inDegree = [0] * n # inDegree 记录每个文件的入度umap = defaultdict(list) # 记录文件依赖关系# 构建图和入度表for s, t in edges:inDegree[t] += 1umap[s].append(t)# 初始化队列，加入所有入度为0的节点queue = deque([i for i in range(n) if inDegree[i] == 0])result = []while queue:cur = queue.popleft()  # 当前选中的文件result.append(cur)for file in umap[cur]:  # 获取该文件指向的文件inDegree[file] -= 1  # cur的指向的文件入度-1if inDegree[file] == 0:queue.append(file)if len(result) == n:print(" ".join(map(str, result)))else:print(-1)if __name__ == "__main__":n, m = map(int, input().split())edges = [tuple(map(int, input().split())) for _ in range(m)]topological_sort(n, edges)