【算法】常用的基础数论
作者:指针不指南吗
专栏:算法篇🐾或许会很慢,但是不可以停下🐾
文章目录
- 1.GCD&LCM
- 2.判断素数(质数)
- 3.分解质因子
1.GCD&LCM
最大公约数&最小共倍数
欧几里得算法——高效
//最大公约数
int gcd(int x,int y)
{return y?gcd(y,x%y):x;
}//最小公倍数
int lcm(int x,int y)
{return x*y/gcd(x,y);
}
2.判断素数(质数)
孪生素数法——高效
- 分析过程如下
首先看一个关于质数分布的规律:大于等于5的质数一定和6的倍数相邻。例如5和7,11和13,17和19等等;
证明:令x≥1,将大于等于5的自然数表示如下:
······ 6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1 ······
可以看到,不在6的倍数两侧,即6x两侧的数为6x+2,6x+3,6x+4,由于2(3x+1),3(2x+1),2(3x+2),所以它们一定不是素数,再除去6x本身,显然,素数要出现只可能出现在6x的相邻两侧。这里要注意的一点是,在6的倍数相邻两侧并不是一定就是质数。此时用一个循环判断质数,可以以6为单元快进,i+=6,加快判断速度。
原因是,假如要判定的数为n,则n必定是6x-1或6x+1的形式,对于循环中6i-1,6i,6i+1,6i+2,6i+3,6i+4,其中如果n能被 6i,6i+2,6i+4整除,则n至少得是一个偶数,但是6x-1或6x+1的形式明显是一个奇数,故不成立;另外,如果n能被6i+3整除,则n至少能被3整除,但是6x能被3整除,故6x-1或6x+1(即n)不可能被3整除,故不成立。
综上,循环中只需要考虑6i-1和6i+1的情况,即循环的步长可以定为6,每次判断循环变量k和k+2的情况即可
bool isprime(int n)
{if(n<=3) //特判几个较小的数return n>1;if(n%6!=1&&n%6!=5) //不在6的倍数的两侧,一定不是素数return 0;for(int i=5;i<=sqrt(n);i+=6) //判断在6的倍数的两侧的数,是不是素数if(n%i==0||n%(i+2)==0)return 0;return 1;
}
3.分解质因子
直接看例题吧
-
题目
链接: AcWing 867. 分解质因数–解释+代码注释 - AcWing
给定 n 个正整数 ai,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
对于每个正整数 ai,按照从小到大的顺序输出其分解质因数后,每个质因数的底数和指数,每个底数和指数占一行。
每个正整数的质因数全部输出完毕后,输出一个空行。
数据范围
1≤n≤100,
2≤ai≤2×10910^9109输入样例:
2 6 8输出样例:
2 1 3 12 3 -
分析
- x 的质因子最多只包含一个大于 根号x 的质数。如果有两个,这两个因子的乘积就会大于 x,矛盾。
- i 从 2 遍历到 根号x。 用 x / i,如果余数为 0,则 i 是一个质因子。
- s 表示质因子 i 的指数,x /= i 为 0,则 s++, x = x / i 。
- 最后检查是否有大于 根号x 的质因子,如果有,输出。
-
代码实现
#include<bits/stdc++.h> using namespace std;void divide(int x) {for (int i = 2; i <= x / i; i ++ )//i <= x / i:防止越界,速度大于 i < sqrt(x)if (x % i == 0)//i为底数{int s = 0;//s为指数while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;//输出}if (x > 1) cout << x << ' ' << 1 << endl;//如果x还有剩余,单独处理cout << endl; }int main() {int n;cin >> n;while (n -- ){int x;cin >> x;divide(x);}return 0; }

相关文章:

【算法】常用的基础数论
作者:指针不指南吗 专栏:算法篇 🐾或许会很慢,但是不可以停下🐾 文章目录1.GCD&LCM2.判断素数(质数)3.分解质因子1.GCD&LCM 最大公约数&最小共倍数 欧几里得算法——高效 //最大公约数 int gcd(int x,i…...

云原生场景下的容器网络隔离技术
云原生场景下的容器网络隔离技术 一、研究背景 随着云计算时代的到来,尤其是容器化技术的飞速发展,云原生作为云计算的未来阶段,其安全势必成为云安全的主要战场。从目前的云原生环境来看,云原生网络安全问题层出不穷࿰…...

用python绘制有向图
目录 添加边权重的有向图思路介绍代码实现效果图设置不同的样式节点和边的有向图思路介绍代码实现效果图下面的Python代码用于绘制有向图,其中使用了 networkx和 matplotlib.pyplot等库。 添加边权重的有向图 思路介绍 首先,创建了一个空的有向图像对象G,并添加了4个节点…...
—官方原版)
Spring MongoDB 开发教程(一)—官方原版
MongoDB支持包含一系列功能:Spring配置支持基于Java的configuration类或Mongo驱动程序实例和副本集的XML命名空间。MongoTemplate帮助类,在执行常见的Mongo操作时提高生产力。包括文档和POJO之间的集成对象映射。将异常转换为Spring的可移植数据访问异常…...
数据结构——二叉搜索树
一、二叉搜索树概念 二叉搜索树又叫二叉排序树,它或是空树,或是具有以下性质的二叉树: (1)若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值; (2)若它的…...

23年5月高项学习笔记3---项目管理概述
项目是创造独特的产品、服务或成果而进行的临时性的工作 独特:每个项目都不一样 可交付成果:某一过程,阶段或项目完成时形成的独特的并且可验证的产品、服务或成果。 临时的:明确的起点和终点、 -------- 项目集: 相…...

【组织架构】中国铁路成都局集团有限公司
0 参考 中国铁路成都局集团有限公司 1 公司介绍 中国铁路成都局集团有限公司,是中国国家铁路集团有限公司管理的18个铁路局集团有限公司之一,简称“成局”,地处中国西南,管辖范围辐射四川、贵州、重庆地区。管内地形复杂&#x…...

剧前爆米花--爪哇岛寻宝】java多线程案例——单例模式、阻塞队列及生产者消费者模型、定时器、线程池
作者:困了电视剧 专栏:《JavaEE初阶》 文章分布:这是关于java多线程案例的文章,进行了对单例模式、阻塞队列及生产者消费者模型、定时器和线程池的讲解,希望对你有所帮助! 目录 单例模式 懒汉模式实现 饿…...

Guitar Pro8中文版更新说明及系统要求介绍
Guitar Pro吉他软件是初学作曲,特别是同时又初学吉他的朋友们的良师益友,是一款极佳的初级软件,是非实时作曲软件之中的一件佳作。Guitar Pro在吉他和弦、把位的显示、推算、查询、调用等方面,也异常方便、简洁、直观和浩瀚&#…...

【id:19】【20分】A. 三数论大小(引用)
题目描述 输入三个整数,然后按照从大到小的顺序输出数值。 要求:定义一个函数,无返回值,函数参数是三个整数参数的引用,例如int &a, int &b, int &c。在函数内对三个参数进行排序。主函数调用这个函数进行…...
)
To_Heart—总结——FWT(快速沃尔什变换)
目录闲话拿来求什么或与异或闲话 这个比FFT简单了很多呢,,大概是我可以学懂的水平! 好像是叫 快速沃尔什变换 ? 拿来求什么 以 FFT 来类比。我们 FFT 可以在 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的复杂度下实现求解࿱…...

Google巨大漏洞让Win10、11翻车,小姐姐马赛克白打了
早年间电脑截图这项技能未被大多数人掌握时,许多人应该都使用过手机拍屏幕这个原始的方式。 但由于较低的画面质量极其影响其他用户的观感,常常受到大家的调侃。 但到了 Win10、11 ,预装的截图工具让门槛大幅降低。 WinShiftS 就能快速打开…...
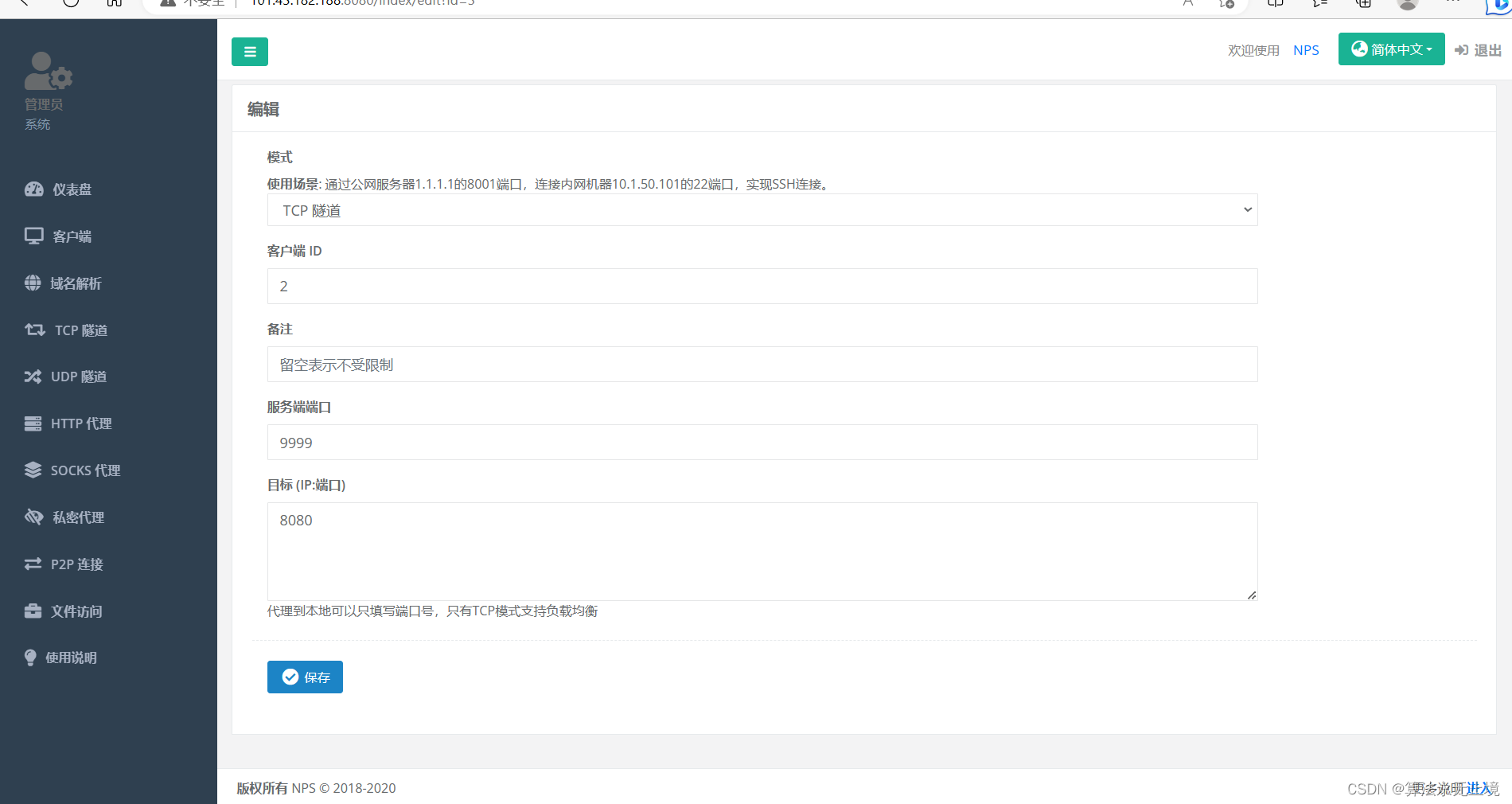
腾讯云服务器部署内网穿透(让其他人在不同ip可以访问我们localhost端口的主机项目)(nps开源项目)
首先打开shell连接我们的云服务器 然后我们再opt目录下面创建一个文件夹用来存放我们的压缩包和文件 mkdir /opt/nps 这个是它官方的安装图解.所以我们按照这个docker安装过程来: 然后我们用docker安装镜像.这样的话比较简单一点 docker pull ffdfgdfg/nps 然后我们查看docker…...

IDS、恶意软件、免杀技术、反病毒技术、APT、对称加密、非对称加密以及SSL的工作过程的技术介绍
IDS的简单介绍IDS是:入侵检测系统(intrusion detection system,简称“IDS”)是一种对网络传输进行即时监视,在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。它与其他网络安全设备的不同之处便在于&…...
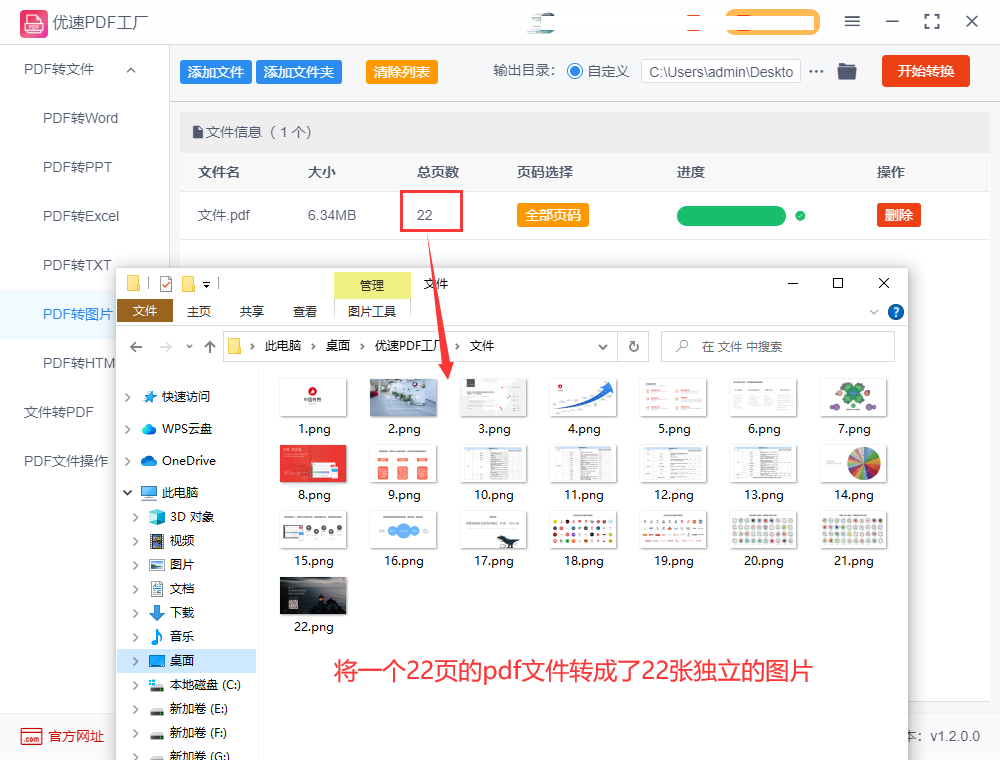
怎么把pdf转换成高清图片
怎么把pdf转换成高清图片?可以使用以下两种方法: 方法一:使用Adobe Acrobat Pro DC 1、打开需要转换的PDF文件,点击“文件”菜单中的“导出为”,在弹出的菜单中选择“图像”,然后选择“JPEG”。 2、在“…...
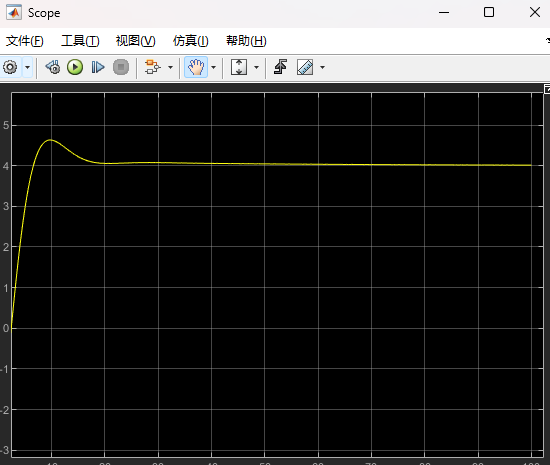
MATLAB 系统辨识 + PID 自动调参
系统辨识 PID 自动调参 文章目录系统辨识 PID 自动调参1. 导入数据1.1 从 Excel 中导入数据2. 系统辨识3. PID 自动调参1. 导入数据 1.1 从 Excel 中导入数据 如果不是从Excel中导入可以跳过该步骤 导入函数: [num,txt,raw]xlsread(xxx\xxx.xlsx);num返回的是…...

【vue3】组合式API之setup()介绍与reactive()函数的使用·上
>😉博主:初映CY的前说(前端领域) ,📒本文核心:setup()概念、 reactive()的使用 【前言】vue3作为vue2的升级版,有着很多的新特性,其中就包括了组合式API,也就是是 Composition API。学习组合…...

爬虫Day3 csv和bs4
爬虫Day3 csv和bs4 一、CSV的读和写 1. 什么是csv文件 csv文件叫做:逗号分隔值文件,像Excel文件一样以行列的形式保存数据,保存数据的时候同一行的多列数据用逗号隔开。 2. csv文件的读写操作 1) csv文件读操作 from csv import reader…...
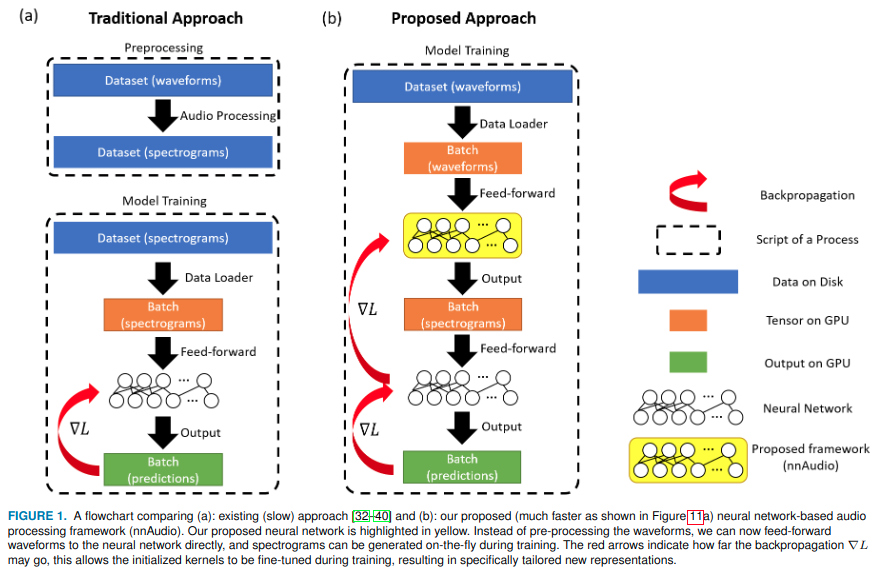
nnAudio的简单介绍
官方实现 https://github.com/KinWaiCheuk/nnAudio; 论文实现: nnAudio: An on-the-Fly GPU Audio to Spectrogram Conversion Toolbox Using 1D Convolutional Neural Networks; 以下先对文章解读: abstract 在本文中&#x…...
)
【id:134】【20分】B. 求最大值最小值(引用)
题目描述 编写函数void find(int *num,int n,int &minIndex,int &maxIndex),求数组num(元素为num[0],num[1],...,num[n-1])中取最小值、最大值的元素下标minIndex,maxIndex(若有相同最值࿰…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
