电子技术——BJT差分输入对
电子技术——BJT差分输入对

本节我们来讨论BJT差分输入对。
共模输入
下图是BJT差分输入对的基本原理图:
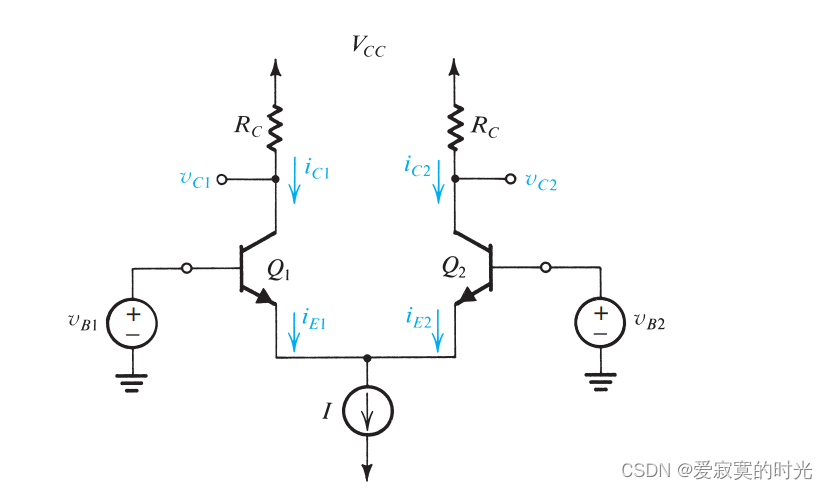
首先我们考虑两端输入共模信号 VCMV_{CM}VCM :
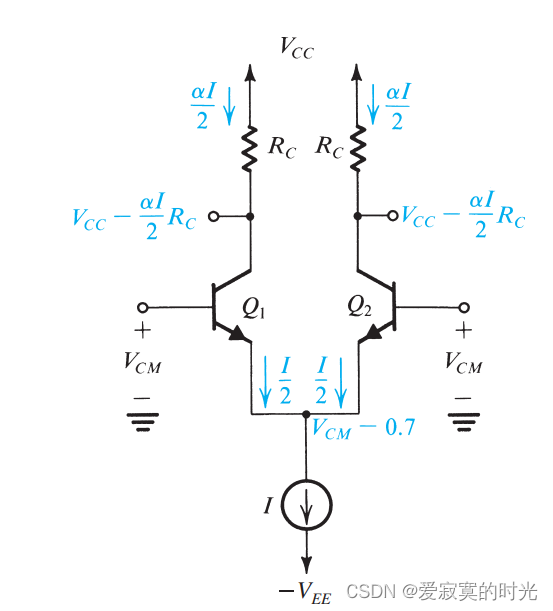
此时 vB1=vB2=VCMv_{B1} = v_{B2} = V_{CM}vB1=vB2=VCM 因为电路的对称结构,所以 iE1=iE2=I/2i_{E1} = i_{E2} = I/2iE1=iE2=I/2 ,发射极电压为 VCM−VBEV_{CM} - V_{BE}VCM−VBE 这里 VBEV_{BE}VBE 是满足电流 iE1=iE2=I/2i_{E1} = i_{E2} = I/2iE1=iE2=I/2 的基极电压(大约在0.7V)。输出的集电极电压为:
vo=VCC−αI2RCv_o = V_{CC} - \frac{\alpha I}{2}R_C vo=VCC−2αIRC
输出端两端电压相同,差值为零。这说明BJT差分输入对同样对共模信号无响应。
对于BJT差分输入对的共模信号输入范围,存在上限,当 Q1Q_1Q1 和 Q2Q_2Q2 处于饱和区边界的时候,此时:
VCMmax≃VC+0.4=VCC−αI2RC+0.4V_{CMmax} \simeq V_C + 0.4 = V_{CC} - \frac{\alpha I}{2}R_C + 0.4 VCMmax≃VC+0.4=VCC−2αIRC+0.4
存在下限,使得电流源 III 有最小的压降 VCSV_{CS}VCS :
VCMmin=−VEE+VCS+VBEV_{CMmin} = -V_{EE} + V_{CS} + V_{BE} VCMmin=−VEE+VCS+VBE
大信号模型
根据BJT的电压电流传导关系,我们知道:
iE1=ISαevB1−vE/VTi_{E1} = \frac{I_S}{\alpha} e^{v_{B1} - v_{E}/V_T} iE1=αISevB1−vE/VT
iE2=ISαevB2−vE/VTi_{E2} = \frac{I_S}{\alpha} e^{v_{B2} - v_{E}/V_T} iE2=αISevB2−vE/VT
做除法得到:
iE1iE2=e(vB1−vB2)/VT\frac{i_{E1}}{i_{E2}} = e^{(v_{B1} - v_{B2})/V_T} iE2iE1=e(vB1−vB2)/VT
以及我们有 iE1+iE2=Ii_{E1} + i_{E2} = IiE1+iE2=I ,解得:
iE1=I1+e−vid/VTi_{E1} = \frac{I}{1 + e^{-v_{id}/V_T}} iE1=1+e−vid/VTI
iE2=I1+evid/VTi_{E2} = \frac{I}{1 + e^{v_{id}/V_T}} iE2=1+evid/VTI
这里 vid=vB1−vB2v_{id} = v_{B1} - v_{B2}vid=vB1−vB2 ,集电极电流等于发射极电流的 α\alphaα 倍,非常接近单位一。
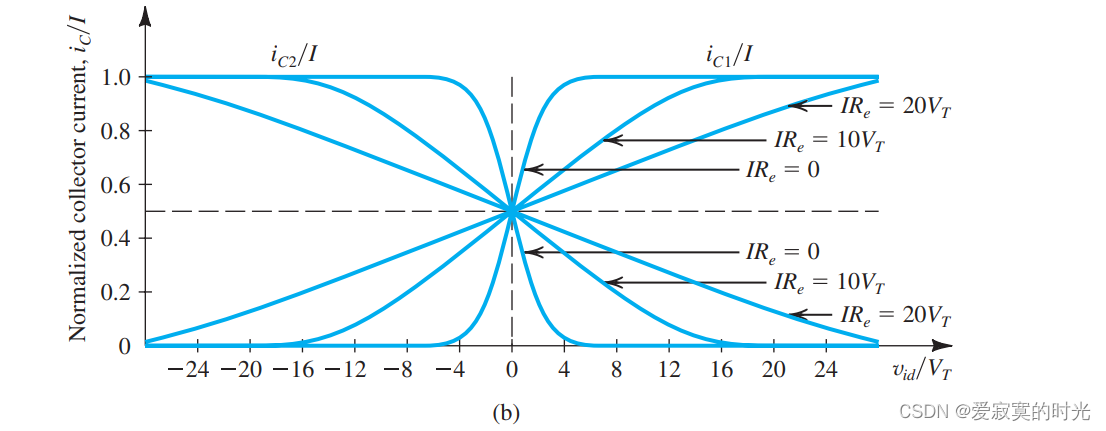
下图展示了归一化之后的差分响应的图形表示:
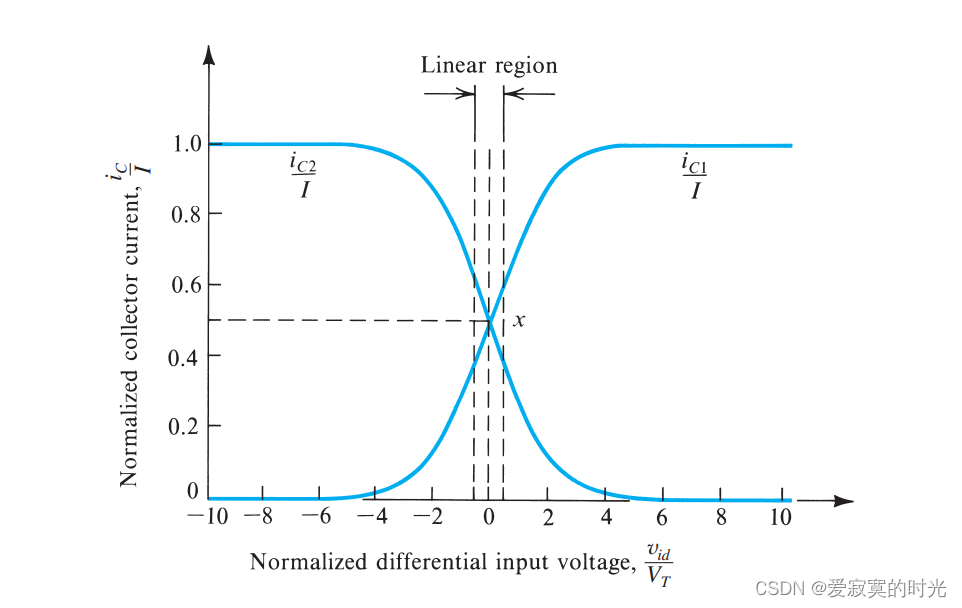
我们发现,当 vid=4VTv_{id} = 4V_Tvid=4VT (100mV)的时候,就会出现一个BJT截止另一个BJT完全导通的的情况,这比MOS的边界 2VOV\sqrt{2}V_{OV}2VOV 要小。实际上,BJT具有从一边切换到另一边更快的速度。
若获得较好的线性区域,必须让输入的差分信号小于 VT/2V_T/2VT/2 。最后,我们介绍一种扩宽BJT线性区域的方法,我们使用发射极电阻,如图所示:
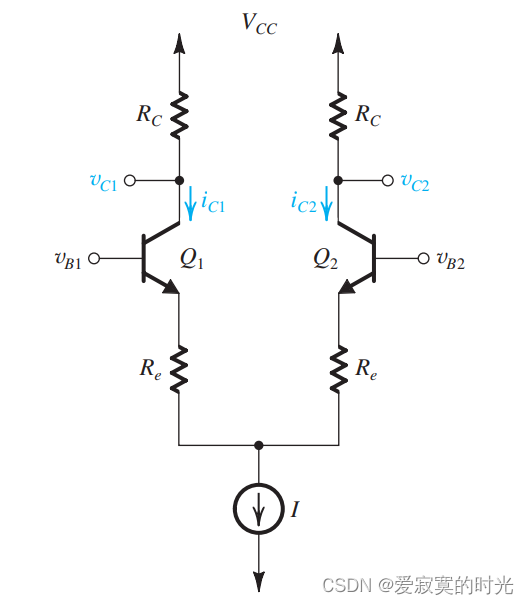
我们之前在BJT章节学习过,引入BJT的发射极电阻之后,由于发射极电阻的分压作用,可以扩大我们信号的幅值范围,进而扩宽BJT线性区域,结果可以参考下图:
但是代价是降低了增益系数。这种方法对于MOS差分输入对同样有效。
小信号模型
下图展示了我们小信号模型的原始电路图:
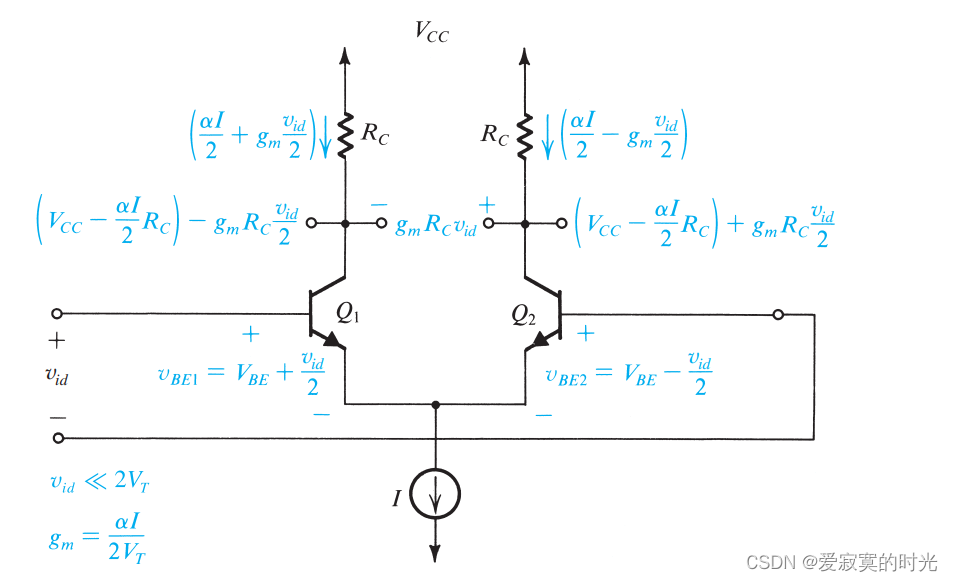
差分信号输入 vidv_{id}vid 通过互补输入到BJT差分输入对。此时集电极的信号电流为:
ic1=αI1+e−vid/VTi_{c1} = \frac{\alpha I}{1 + e^{-v_{id}/V_T}} ic1=1+e−vid/VTαI
ic2=αI1+evid/VTi_{c2} = \frac{\alpha I}{1 + e^{v_{id}/V_T}} ic2=1+evid/VTαI
将 ic1i_{c1}ic1 的分子分母同时乘以 evid/2VTe^{v_{id}/2V_T}evid/2VT :
ic1=αIevid/2VTevid/2VT+e−vid2/VTi_{c1} = \frac{\alpha I e^{v_{id}/2V_T}}{e^{v_{id}/2V_T} + e^{-v_{id}2/V_T}} ic1=evid/2VT+e−vid2/VTαIevid/2VT
假设 vid≪2VTv_{id} \ll 2V_Tvid≪2VT ,我们 exe^xex 展开只保留前两项:
ic1≃αI(1+vid/2VT)1+vid/2VT+1−vid/2VT=αI2+αI2VTvid2i_{c1} \simeq \frac{\alpha I(1+v_{id}/2V_T)}{1+v_{id}/2V_T + 1-v_{id}/2V_T} = \frac{\alpha I}{2} + \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic1≃1+vid/2VT+1−vid/2VTαI(1+vid/2VT)=2αI+2VTαI2vid
同理:
ic1≃αI2−αI2VTvid2i_{c1} \simeq \frac{\alpha I}{2} - \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic1≃2αI−2VTαI2vid
所以BJT差分输入对的差分电流为:
ic=αI2VTvid2i_c = \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic=2VTαI2vid
这表明,当应用差分信号输入 vidv_{id}vid 的时候, ic1i_{c1}ic1 会增加 ici_cic 而 ic2i_{c2}ic2 会降低 ici_cic 但保持总量不变一直为 III 。
另外一种解释为,BJT的互导系数为:
gm=ICVT=αI/2VTg_m = \frac{I_C}{V_T} = \frac{\alpha I/2}{V_T} gm=VTIC=VTαI/2
对于每一个BJT的输入信号电压都是 vid2\frac{v_{id}}{2}2vid ,故写作是:
ic=gmvid2i_c = g_m \frac{v_{id}}{2} ic=gm2vid
同样我们可以使用T模型解释:
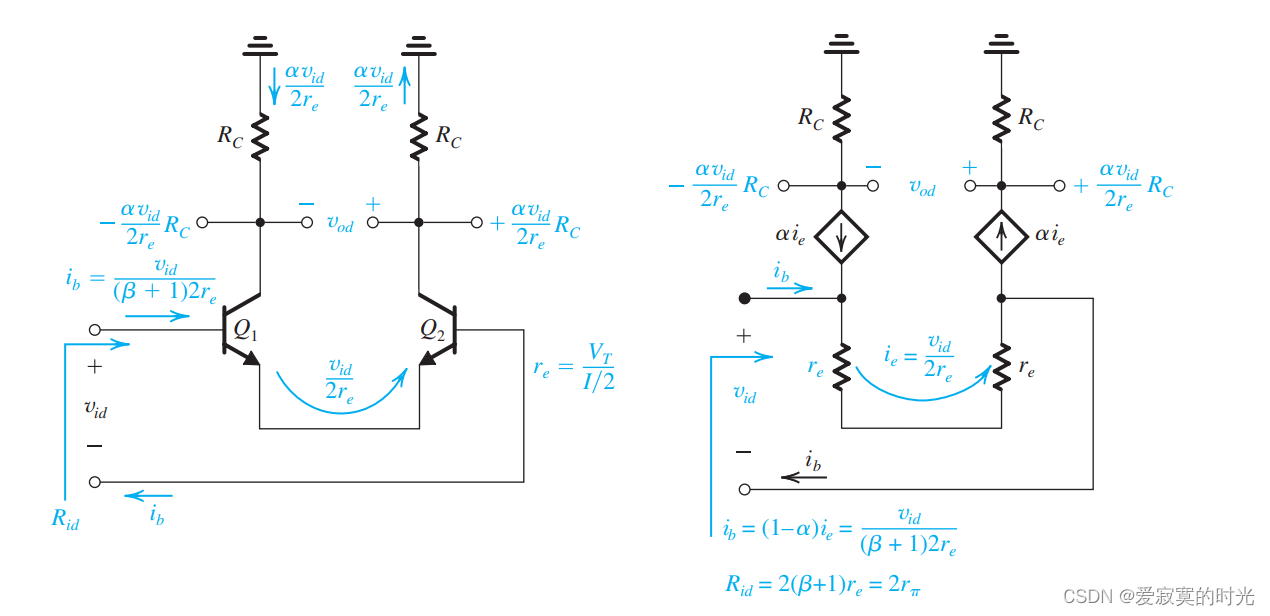
根据基尔霍夫定律,电压 vidv_{id}vid 作用在 2re2r_e2re 的总电阻中,此时:
ie=vid2rei_e = \frac{v_{id}}{2 r_e} ie=2revid
则此时的集电极电流为:
ic=αvid2re=gmvid2i_c = \alpha \frac{v_{id}}{2 r_e} = g_m \frac{v_{id}}{2} ic=α2revid=gm2vid
同样的分析方法适用于分析带发射极电阻的情况,如图:
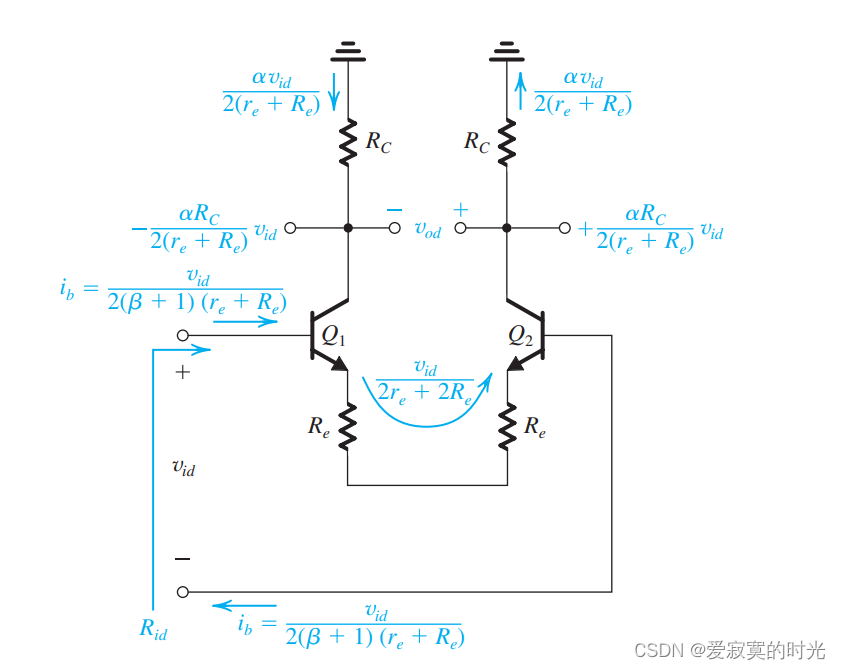
此时:
ie=vid2re+2Rei_e = \frac{v_{id}}{2r_e + 2R_e} ie=2re+2Revid
BJT不像MOS存在无穷大阻抗,现在让我们来计算BJT差分输入对的输入阻抗,我们知道两个输入端的基极电流相等,且都为:
ib=ieβ+1=vid/2reβ+1i_b = \frac{i_e}{\beta + 1} = \frac{v_{id}/2r_e}{\beta + 1} ib=β+1ie=β+1vid/2re
因此输入阻抗为:
Rid≡vidib=(β+1)2re=2rπR_{id} \equiv \frac{v_{id}}{i_b} = (\beta + 1)2r_e = 2r_\pi Rid≡ibvid=(β+1)2re=2rπ
这同样遵循电阻反射定律,即从两个基极看过去的电阻等于发射极电阻的 β+1\beta + 1β+1 倍。所以带发射极电阻的输入阻抗为:
Rid=2(β+1)(re+Re)R_{id} = 2(\beta + 1)(r_e + R_e) Rid=2(β+1)(re+Re)
接下来考虑电压增益,我们知道输出端的电压为:
vC1=(VCC−ICRC)−gmRCvid2v_{C1} = (V_{CC} - I_CR_C) - g_mR_C\frac{v_{id}}{2} vC1=(VCC−ICRC)−gmRC2vid
vC2=(VCC−ICRC)+gmRCvid2v_{C2} = (V_{CC} - I_CR_C) + g_mR_C\frac{v_{id}}{2} vC2=(VCC−ICRC)+gmRC2vid
这里 gmg_mgm 是BJT偏置在电流为 ICI_CIC 处的互导系数,且 ICI_CIC 为:
IC=αI2I_C = \frac{\alpha I}{2} IC=2αI
当使用差分输出的时候,此时电压增益为:
Ad=vodvid=gmRCA_d = \frac{v_{od}}{v_{id}} = g_mR_C Ad=vidvod=gmRC
当使用发射极电阻的时候,电压增益为:
Ad=α(2RC)2re+2Re≃RCre+ReA_d = \frac{\alpha (2R_C)}{2r_e + 2R_e} \simeq \frac{R_C}{r_e + R_e} Ad=2re+2Reα(2RC)≃re+ReRC
这同样满足电压增益为集电极总电阻比上发射极总电阻。
下图展示了一个不同的BJT差分输入对:
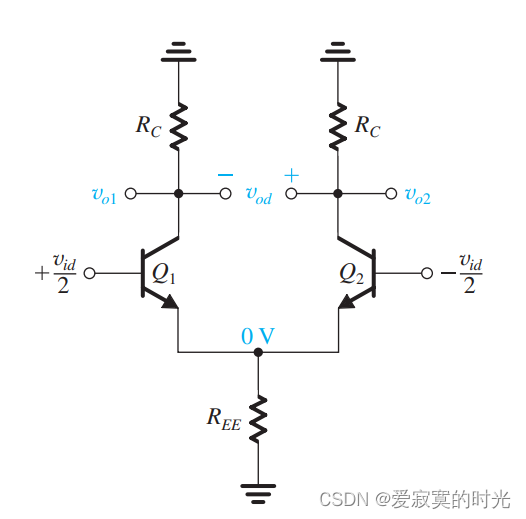
图中我们使用的互补输入方式,而且我们使用共发射极电阻 REER_{EE}REE 来代替偏置的恒流源,因为电路总是对称的,所以共发射极节点处的电压总是是为零,因此上面的电路等效于下面的半电路:
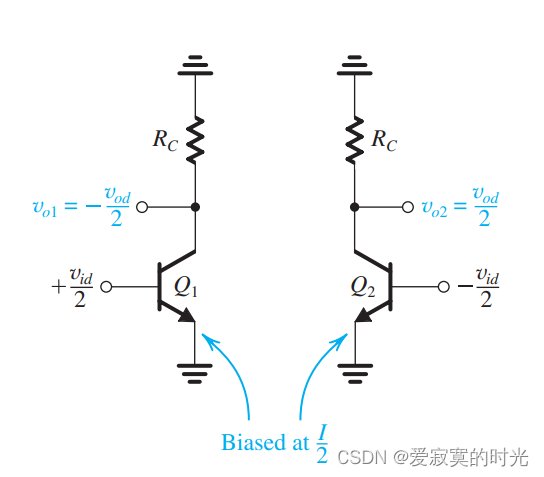
虽然 REER_{EE}REE 的阻抗是有限的,但是这并不影响信号分析中,BJT的发射极永远是虚拟AC地,因此 REER_{EE}REE 的有限阻抗不影响BJT差分输入对。
有时候,并不总是使用互补输入方式,另一种可能的输入方式是一端接地,一端输入,如图:
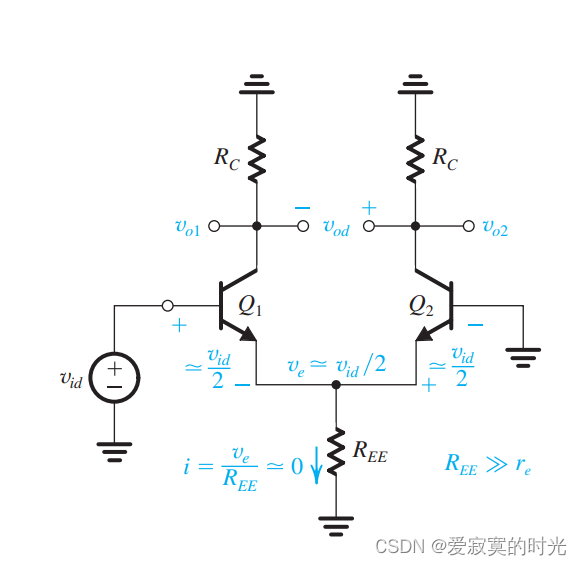
此时发射极电压不再是零,电阻 REER_{EE}REE 对信号存在影响。若假设 REE≫reR_{EE} \gg r_eREE≫re 则可以近似的看成是 ve=vid/2v_e = v_{id} / 2ve=vid/2 ,此时整个电路等价于互补输入方式,半电路分析仍可以使用,如上图。
互补输入方式中,两个半电路完全一致,因此只需要分析电路的一半即可,这种方法称为 差分半电路 。我们将其中一个半电路使用混合 π\piπ 模型:
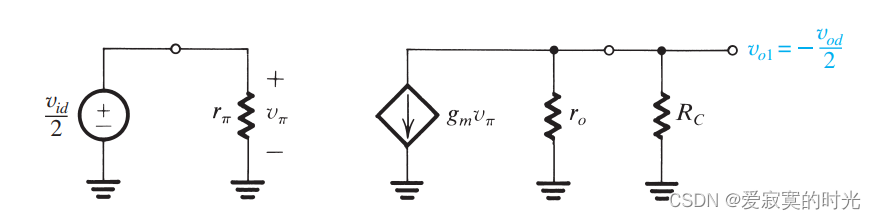
分析方法和我们之前分析共发射极电路分析方法一致,此时偏置电流为 I/2I/2I/2 。若考虑 ror_oro 的影响,我们有:
Ad=gm(RC∣∣ro)A_d = g_m(R_C || r_o) Ad=gm(RC∣∣ro)
BJT差分输入对的输入阻抗是半电路输入阻抗的两倍。
相关文章:

电子技术——BJT差分输入对
电子技术——BJT差分输入对 本节我们来讨论BJT差分输入对。 共模输入 下图是BJT差分输入对的基本原理图: 首先我们考虑两端输入共模信号 VCMV_{CM}VCM : 此时 vB1vB2VCMv_{B1} v_{B2} V_{CM}vB1vB2VCM 因为电路的对称结构,所以 i…...
[MySQL教程②] - MySQL介绍和发展史
目录 ❤ MySQL介绍 ❤ 什么是数据库 ❤ 什么是数据 ❤ 数据库管理系统 ❤ NoSQL特性总览 ❤ NoSQL的分类、特点、典型产品 ❤ 常见的数据库产品有哪些? ❤ Oracle公司产品介绍 Oracle数据库版本介绍 Oracle的市场应用 MySQL数据库版本介绍 MyS…...

多表查询--实例
1 创建student和score表 CREATE TABLE student ( id INT(10) NOT NULL UNIQUE PRIMARY KEY , name VARCHAR(20) NOT NULL , sex VARCHAR(4) , birth YEAR, department VARCHAR(20) , address VARCHAR(50) ); 创建score表。SQL代码如下: CREATE TABLE score ( id INT…...

Differentially Private Grids for Geospatial Data
文章目录abstractintroabstract 在本文中,我们解决了为二维数据集(如地理空间数据集)构建差异私有概要的问题。目前最先进的方法通过执行数据域的递归二进制分区和构造分区的层次结构来工作。我们表明,基于分区的概要方法的关键挑战在于选择正确的分区粒…...

Java学习记录day8
类与对象 继承例题 https://www.bilibili.com/video/BV1PU4y1E7nX?p55&vd_source8f80327daa664c039f5c342a25bcbbae(B站千峰马剑威Java基础入门视频第P55,记录的重要学习内容之一) final关键字 作用: 声明一个常量&…...

Solon2 开发之容器,三、注入或手动获取 Bean
1、如何注入Bean? 先了解一下Bean生命周期的简化版: 运行构建函数尝试字段注入(有时同步注入,没时订阅注入。不会有相互依赖而卡住的问题)Init 函数(是在容器初始化完成后才执行)…释放&#…...

微信小程序_调用openAi搭建虚拟伙伴聊天
微信小程序_调用openAi搭建虚拟伙伴聊天背景效果关于账号注册接口实现8行python搞定小程序实现页面结构数据逻辑结速背景 从2022年的年底,网上都是chagpt的传说,个人理解这个chatgpt是模型优化训练,我们在用chatgpt的时候就在优化这个模型&a…...
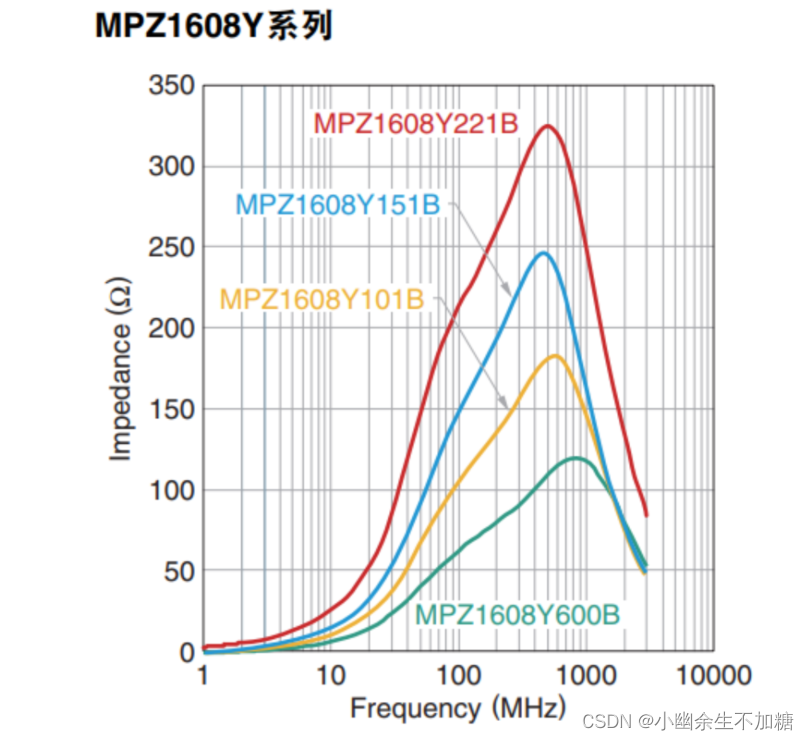
硬件工程师入门基础知识(一)基础元器件认识(一)
硬件工程师入门基础知识 (一)基础元器件认识(一) 今天水一篇hhh。介绍点基础但是实用的东西。 tips:学习资料和数据来自《硬件工程师炼成之路》、百度百科、网上资料。 1.贴片电阻 2.电容 3.电感 4.磁珠 1.贴片电…...
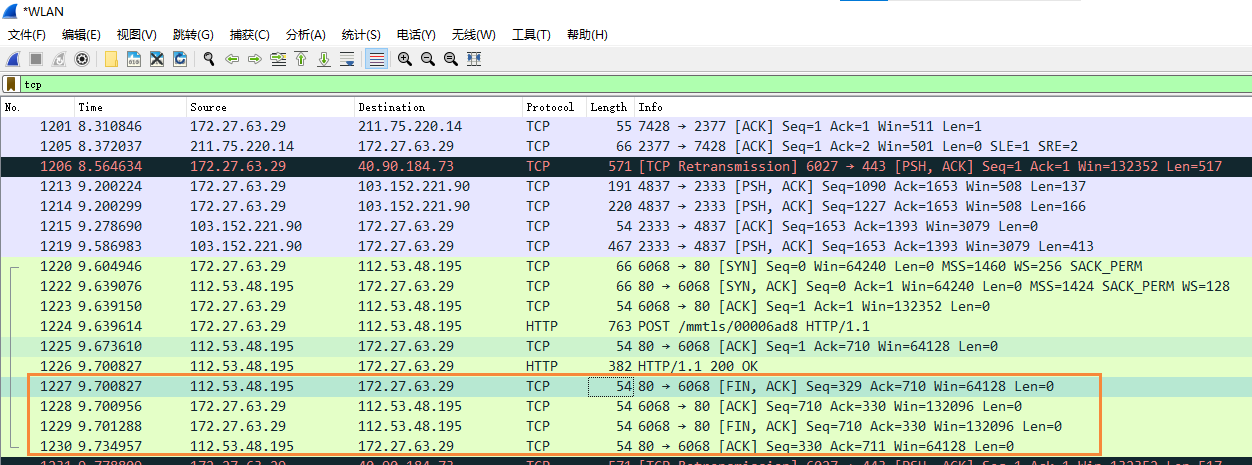
TCP的运输连接管理
TCP的运输连接管理 文章目录TCP的运输连接管理TCP报文格式简介首部各个字段的含义控制位(flags)TCP的连接建立抓包验证一些细节及解答TCP连接释放抓包验证一些细节及解答参考TCP是面向连接的协议。运输连接是用来传送TCP报文的。TCP运输连接的建立和释放时每一次面向连接的通信…...

地级市用电、用水、用气数据指标
用电用水量和煤气及液化石油气供应及利用情况可以反映出城市基础设施的建设情况!之前我们基于历年的《中国城市统计年鉴》整理了1999—2020年的人口数量数据指标、人口变动数据指标、用地相关数据指标、污染物排放和环境治理相关数据指标、地区生产总值及一二三产构…...

安装deepinlinuxV20.8配置docker和vscode开发c语言
# 重装的原因 某个开发任务时,发现需要glibc2.25,本机版本比较低,就下载源码configure make makeinstall,结果失败了, 看来与系统用的glibc有冲突,造成部分库版本不一致,打开终端出现段错误&#x…...
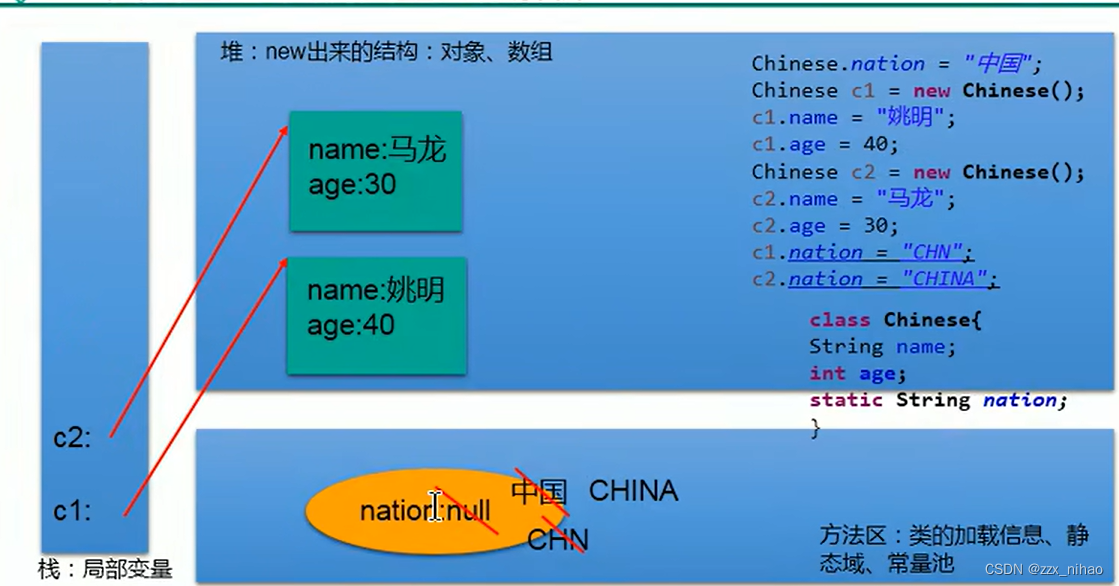
java08-面向对象3
一:static 关键字:静态的 1.可以用来修饰的结构:主要用来修饰类的内部结构 属性、方法、代码块、内部类 2. static 修饰属性:静态变量(或类变量) 2.1 属性,是否使用static修饰,又分为静态属…...
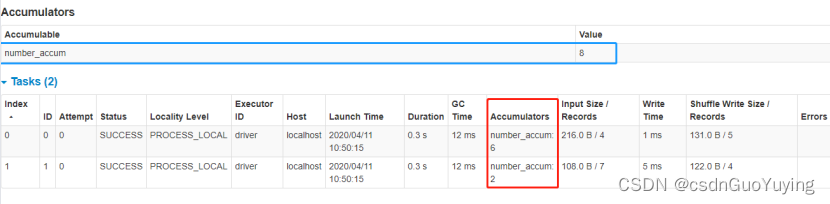
【Spark分布式内存计算框架——Spark Core】8. 共享变量
第七章 共享变量 在默认情况下,当Spark在集群的多个不同节点的多个任务上并行运行一个函数时,它会把函数中涉及到的每个变量,在每个任务上都生成一个副本。但是,有时候需要在多个任务之间共享变量,或者在任务(Task)和…...

C++多态常见面试题
1.什么是多态 简单点说,就是多种形态,具体就是完成某个行为,当不同的对象去完成时产生的不同形态。多态分为静态多态和动态多态,静态多态一般指的是函数重载,在编译阶段通过函数名修饰规则,不同类型调用不同…...
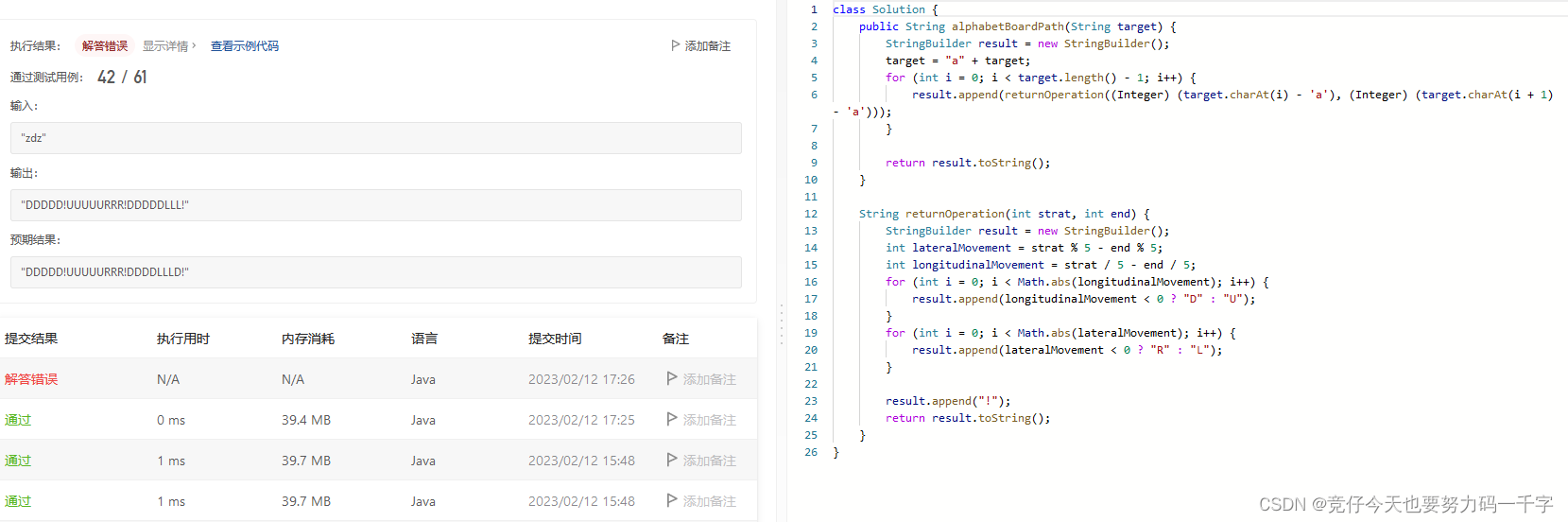
字母板上的路径 题解,力扣官方出来挨打(小声)
字母板上的路径 我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board [“abcde”, “fghij”, “klmno”, “pqrst”, “uvwxy”, “z”],如下所示。 我们可以按下面的指令规则行动:…...
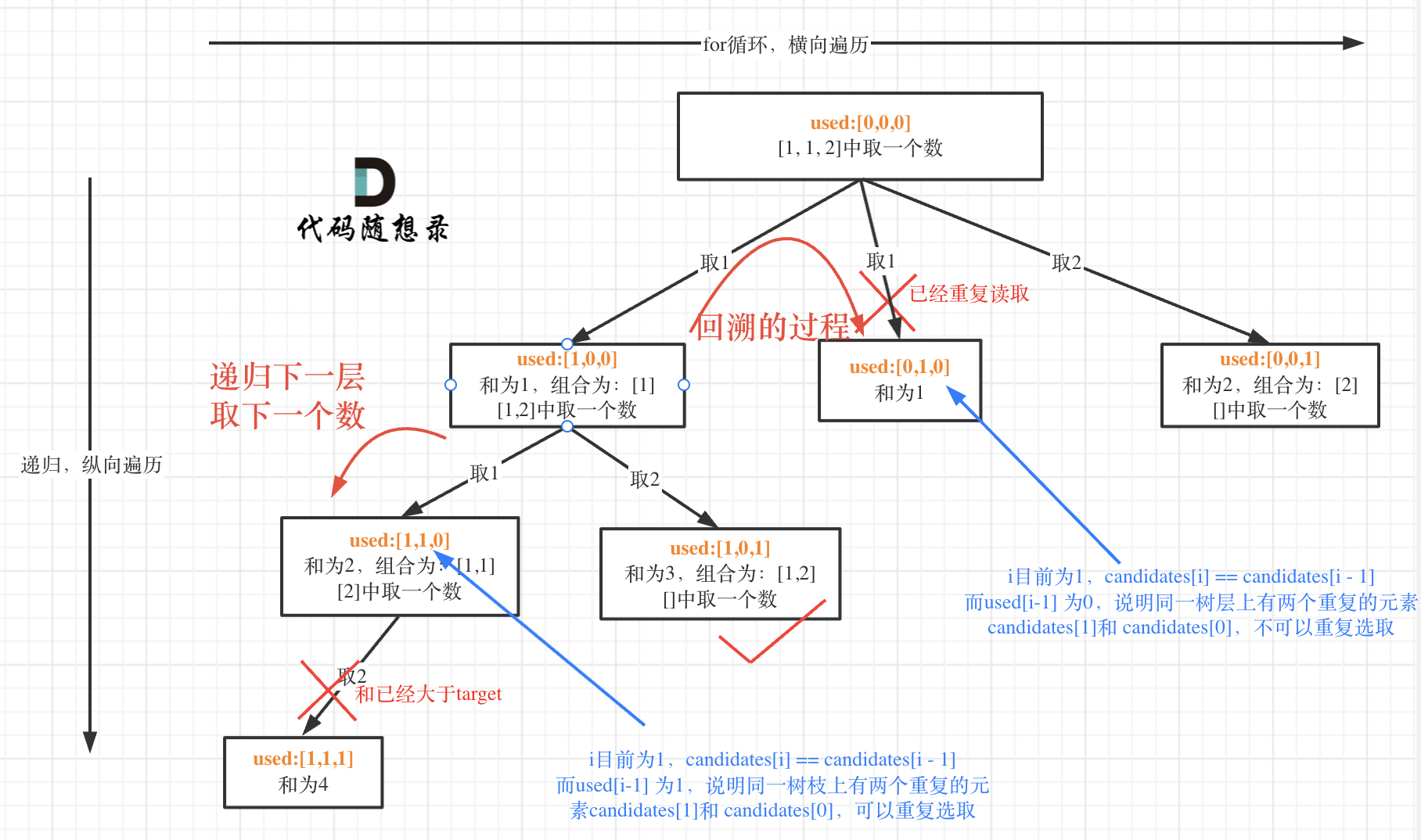
代码随想录算法训练营第二十六天 | 39. 组合总和,40.组合总和II,131.分割回文串
一、参考资料组合总和题目链接/文章讲解:https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html 视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ 组合总和II题目链接/文章讲解:https://programmercarl.com/004…...

vueday01-脚手架安装详细
一、vue脚手架安装命令npm i -g vue/cli 或 yarn global add vue/cli安装上面的工具,安装后运行 vue --version ,如果看到版本号,说明安装成功或 vue -V工具安装好之后,就可以安装带有webpack配置的vue项目了。创建项目之前&#…...
)
初识cesium3d(一)
使用ViteVue3.2Cesium。Vite需要Node.js版本14.18及以上版本。Vite命令创建的工程会自动生成vite.config.js文件,来配置一些相关的参数。 1、使用Vite创建vue3项目 # npm npm init vitelatest cesium-app -- --template vue # yarn yarn create vite cesium-app…...

点云转3D网格【Python】
推荐:使用 NSDT场景设计器 快速搭建 3D场景。 在本文中,我将介绍我的 3D 表面重建过程,以便使用 Python 从点云快速创建网格。 你将能够导出、可视化结果并将结果集成到您最喜欢的 3D 软件中,而无需任何编码经验。 此外࿰…...
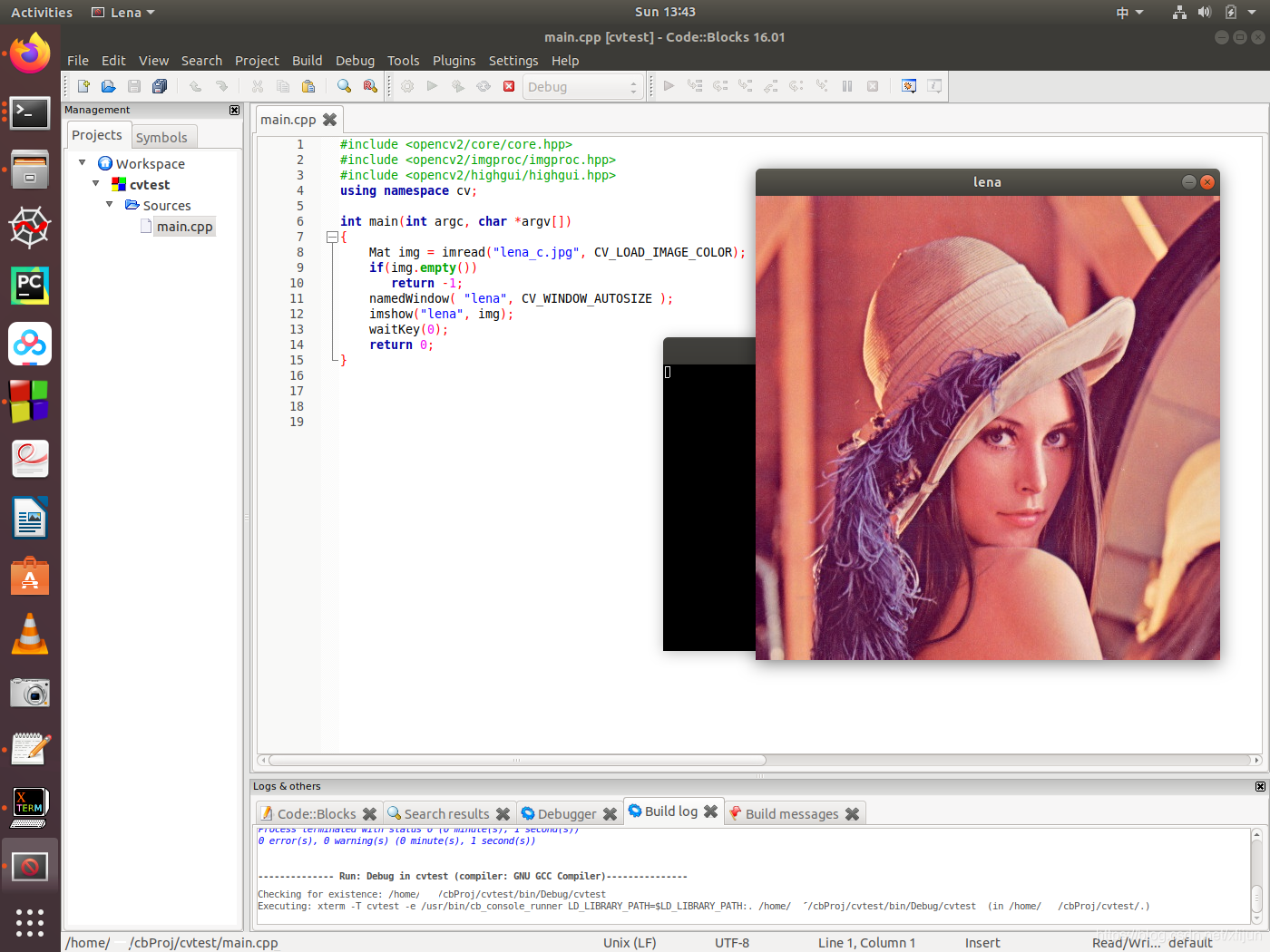
【OpenCV图像处理系列一】OpenCV开发环境的安装与搭建(Ubuntu + Window都适用)
🔗 运行环境:OpenCV,Ubuntu,Windows 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### &#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
