堆排序,快速排序
目录
1.堆排序
2.快速排序
1.hoare版本
2.挖坑法
3.前后指针法
注意点
1.堆排序
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
void adjustdown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);}else{break;}parent = child;child = parent * 2 + 1;}
}
void heapsort(int* a, int n)
{for (int i = (n - 1 -1) / 2; i >= 0; i--){adjustdown(a, n, i);}for (int i = n-1; i > 0; i--){Swap(&a[0], &a[i]);adjustdown(a, i, 0);}
}void printarr(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
void heaptest()
{int arr[] = { 4,7,1,9,3,6,5,8,3,2,0 };printarr(arr, sizeof(arr)/sizeof(int));heapsort(arr, sizeof(arr)/sizeof(int));printarr(arr, sizeof(arr)/sizeof(int));
}
我们先用向下调整算法建堆。
使用向下调整算法建堆的前提是,该节点的子树都是堆。那么我们从最后一个节点的父节点开始向下调整算法,这样因为两个子树都是叶子节点,因此满足条件。从后往前,一直遍历到父节点为根节点,那么就建好堆了。
然后只需要不断将第一个和最后一个节点的值交换,把最大值放到末尾,然后不断从根节点向下建堆,即可每次都挑选出最大值,我们依次把他们放到末尾即可。
2.快速排序
主逻辑,递归

1.hoare版本
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void printarr(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}int partsort(int* a, int left, int right)
{int keyi = left;while (left < right){while (left < right &&a[left] <= a[keyi]){left++;}while (left < right && a[right] >= a[keyi]){right--;}Swap(&a[left], &a[right]);//如果是因为left==right结束,交换值也并不影响结果}Swap(&a[keyi], &a[left]);return left;
}void quicksort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = partsort(a, begin, end);quicksort(a, begin, keyi-1);quicksort(a, keyi + 1, end);
}void quicktest()
{int arr[] = { 4,7,1,9,3,6,5,8,3,2,0 };printarr(arr, sizeof(arr) / sizeof(int));quicksort(arr,0, sizeof(arr) / sizeof(int)-1);printarr(arr, sizeof(arr) / sizeof(int));
}我们以左边第一个下标为keyi,因此先从右边开始找
1.先从右往左找到比a【keyi】小的值
2.再从左往右找到比a【keyi】大的值
交换这两个值。
3.不断重复以上过程直到相遇left == right
4.交换a【keyi】和a【left】
注意点
1.我们在移动下标时,判断条件是a[left] <= a[keyi]left++
a[right] >= a[keyi] right--
这是为了防止遇到与a【keyi】相等的值的时候,陷入死循环

2.我们在寻找下标的小循环中也加入left<right的判断是因为防止极端情况。
如果不判断就会越界,而且如果是因为left==right结束,交换值也并不影响结果
同时因为这个极端情况原因,我们遍历是从最左边keyi处开始遍历,不然会忽略掉这种情况。也是注意点1中判断条件需要加=的原因

3.我们再来谈谈为什么从一边开始调整要从另一边开始找起
以上面的情况为例子,
因为这样可以保证他们相遇时候所处在的值一定比a【keyi】小
情况1、left不动,right先移动与left相遇,此时a【keyi】还在原位
情况2. right移动后找到小值,left移动后与right相遇,此时该位置的值比a【keyi】小
情况3,left与right先各自移动并且交换一次,然后right再移动和left相遇,此时因为已经交换过,a【left】处储存的值小于a【keyi】因此也符合
综上
2.挖坑法
int partsort(int* a, int left, int right)
{int key = a[left];while (left < right){while (left < right && a[right] >= key){right--;}a[left] = a[right];while (left < right && a[left] <= key){left++;}a[right] = a[left];}a[left] = key;return left;}





把a【keyi】的位置先挖走,记录这个key值。
1.从右边往左找小,把这个值填入坑中,同时这个位置形成一个新的坑
2.从左边往右找大 把这个值填入坑中,同时这个位置形成一个新的坑
3.重复以上操作,直到left==right,然后把key值填入这个坑中,此时这个位置一定是坑,因为left和right永远有一个是坑
3.前后指针法
int partsort(int* a, int left, int right)
{int prev = left;int cur = left + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)//这里直接判断一下,相等就不交换,并且在判断条件 //的地方就更新prev{Swap(&a[prev], &a[cur]);}++cur;//cur就是一直往前走,直到结束,遇到相应位置才有操作,因此直接放到循环中}Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;}cur一直向后找小于key的位置
如果a【cur】< key
++prev,然后交换a【prev】和a【cur】
如果cur所在位置的值都比key小,那么cur和prev拉不开差距.++prev后和cur交换就是自身交换

如果遇到比key大的值,就会拉开差距,此时如果cur遇到比key小的值,这个值就会和一个比key大的值交换,因为prev和cur原本中间隔着的都是大于key的值,++prev后再交换就会是这样的结果


这样相当于把大的往右推,小的往左推

cur走出数组结束,key与a【prev】交换即可
注意点
以上三种方法只是实现形式不同,时间复杂度是完全相同的,并且主逻辑的代码不需要更改,就是一个递归,只需要把部分排序修改即可
相关文章:

堆排序,快速排序
目录 1.堆排序 2.快速排序 1.hoare版本 2.挖坑法 3.前后指针法 注意点 1.堆排序 void Swap(int* a, int* b) {int tmp *a;*a *b;*b tmp; } void adjustdown(int* a, int n, int parent) {int child parent * 2 1;while (child < n){if (child 1 < n &&am…...

系统架构师---数据库设计的四个阶段
需求分析、概念设计、逻辑设计和物理设计是数据库设计中的四个关键阶段,每个阶段都有其独特的任务和目标,以下是对这四个阶段的区别的详细阐述: 需求分析阶段 目标:全面理解用户对数据库系统的需求,包括业务需求、信…...

MySQL_简介及安装、配置、卸载(超详细)
课 程 推 荐我 的 个 人 主 页:👉👉 失心疯的个人主页 👈👈入 门 教 程 推 荐 :👉👉 Python零基础入门教程合集 👈👈虚 拟 环 境 搭 建 :…...

大数据处理技术:分布式文件系统HDFS
目录 1 实验名称: 2 实验目的 3 实验内容 4 实验原理 5 实验过程或源代码 5.1 HDFS的基本操作 5.2 HDFS-JAVA接口之读取文件 5.3 HDFS-JAVA接口之上传文件 5.4 HDFS-JAVA接口之删除文件 6 实验结果 6.1 HDFS的基本操作 6.2 HDFS-JAVA接口之读取文件 6.…...
组合数(模板)
1.杨辉三角求组合数,最高只能求几千内的组合数。 #include<bits/stdc.h> using namespace std; #define int long long int C[1005][1005]; signed main() {//求 1000 以内的组合数 for(int i0;i<1000;i){C[i][0]C[i][i]1;for(int j1;j<i;j){C[i][j]C[…...
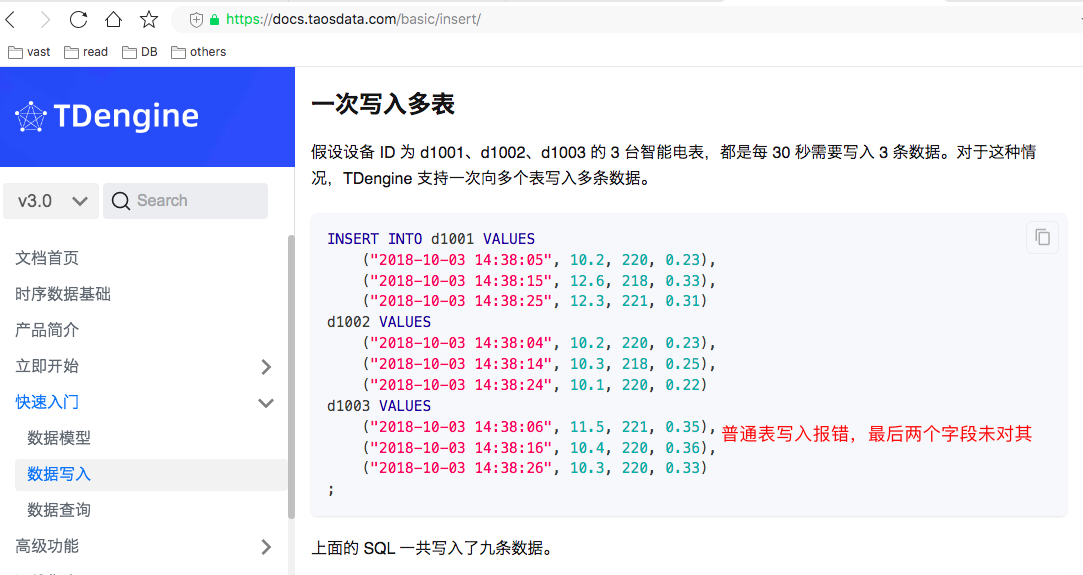
时序数据库 TDengine 的入门体验和操作记录
时序数据库 TDengine 的学习和使用经验 什么是 TDengine ?什么是时序数据 ?使用RPM安装包部署默认的网络端口 TDengine 使用TDengine 命令行(CLI)taosBenchmark服务器内存需求删库跑路测试 使用体验文档纠错 什么是 TDengine &…...

Qt-QPushButton按钮类控件(22)
目录 描述 使用 给按钮添加图片 给按钮添加快捷键 添加槽函数 添加快捷键 添加组合键 开启鼠标的连发功能 描述 经过上面的一些介绍,我们也尝试的使用过了这个控件,接下来我们就要详细介绍这些比较重要的控件了 使用 给按钮添加图片 我们创建…...

镜舟科技与中启乘数科技达成战略合作,共筑数据服务新生态
当今企业数据管理日益规范化,数据应用系统随着数据类型与数量的增长不断细分,为了提升市场竞争力与技术实力,数据领域软件服务商与上下游伙伴的紧密对接与合作显得尤为重要。通过构建完善的生态系统,生态内企业间能够整合资源、共…...

蒸!--数据在内存中的存储
一.整数在内存中的存储 对于整形来说:数据存放内存中其实存放的是补码。 为什么? 在计算机系统中,数值⼀律⽤补码来表⽰和存储。 原因在于,使⽤补码,可以将符号位和数值域统⼀处理; 同时,加法和…...

利用AI增强现实开发:基于CoreML的深度学习图像场景识别实战教程
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

每个企业都需要 (但未使用) 的 BYOD 安全解决方案
远程办公模式的转变彻底改变了组织管理员工设备的方式。如今,员工希望能够灵活地在任何地方使用任何设备工作,这导致自带设备 (BYOD) 政策被广泛采用。 但随着越来越多的企业采用BYOD,一个问题依然摆在眼前:如何在不侵犯个人隐私…...

【多系统萎缩患者必看】科学锻炼秘籍,让生命之树常青
亲爱的小红书朋友们,👋 今天我们要聊一个温暖而坚韧的话题——关于多系统萎缩(MSA)患者的锻炼指南。在这个充满挑战的旅程中,锻炼不仅是身体的锻炼,更是心灵的滋养,是对抗病魔的勇敢姿态&#x…...

【Android】Room—数据库的基本操作
引言 在Android开发中,数据持久化是一个不可或缺的部分。随着应用的复杂度增加,选择合适的数据存储方式变得尤为重要。Room数据库作为Android Jetpack架构组件之一,提供了一种抽象层,使得开发者能够以更简洁、更安全的方式操作SQ…...

「数组」堆排序 / 大根堆优化(C++)
目录 概述 核心概念:堆 堆结构 数组存堆 思路 算法过程 up() down() Code 优化方案 大根堆优化 Code(pro) 复杂度 总结 概述 在「数组」快速排序 / 随机值优化|小区间插入优化(C)中,我们介绍了三种基本排序中的冒泡…...

Edegex Foundry docker和源码安装
edgex文档下载 https://github.com/edgexfoundry/edgex-docs/branches/all 在线文档查看 首先要安装python3环境 然后后安装 打开超级终端 #pip3 install mkdocs #mkdocs serve 在浏览器中输入 http://127.0.0.1:8000/edgex-docs/2.3/ 即可打开在线文档 edgex入门可以参考…...

阿里P8和P9级别有何要求
阿里巴巴的P8和P9级别,代表着公司的资深技术专家或管理者岗位,要求候选人具有丰富的职业经历、深厚的技术能力以及出色的领导力。以下是对P8和P9级别的要求、考察点以及准备建议的详细分析。 P8 级别要求 1. 职业经历: 8年以上的工作经验&a…...
【目标检测数据集】锯子数据集1107张VOC+YOLO格式
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):1107 标注数量(xml文件个数):1107 标注数量(txt文件个数):1107 标注…...

移动产业处理器接口(MIPI)协议是什么?
未来汽车的宏伟愿景备受瞩目,特别是驱动这些汽车的技术更是成为焦点。如今,传感器对于汽车视觉和安全技术的下一阶段至关重要,因为驾驶员和乘客都依赖于它们。这些传感器能够支持众多应用,这些应用往往基于人工智能(AI…...
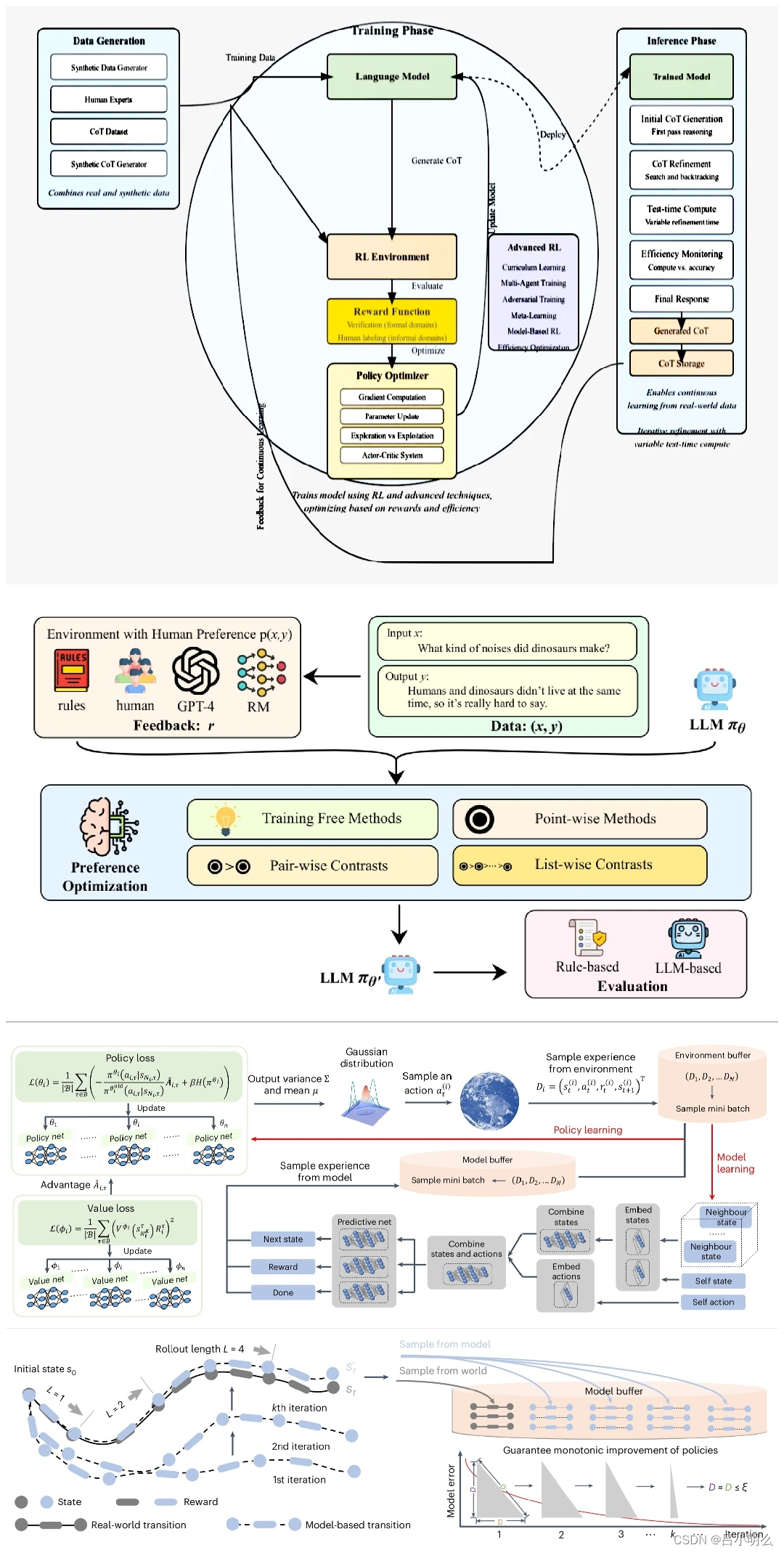
OpenAI o1:隐含在训练与推理间的动态泛化与流形分布
随着OpenAI o1发布,进一步激发了产业与学术各界对AGI的期待以及new scaling law下的探索热情,也看到来自社区和专业机构对o1的阐释,但总感觉还差点什么,因此决定以自己的角度分篇幅梳理下,并分享给大伙: O…...

沉浸式体验和评测Meta最新超级大语言模型405B
2024年7月23日, 亚马逊云科技的AI模型托管平台Amazon Bedrock正式上线了Meta推出的超级参数量大语言模型 - Llama 3.1模型,小李哥也迫不及待去体验和试用了该模型,那这么多参数量的AI模型究竟强在哪里呢?Llama 3.1模型是Meta&…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
