python-素数中的等差数列
题目描述
质数是在数论中很有意思的数,有很多题都可以围绕它来出,就如你眼前所见的这道题。
给定一个闭区间 [a,b] ,将此范围内的所有素数进行从小到大排序,对于连续的素数,我们可以发现很多等差数列(元素个数大于等于 3 ),现在就请你完成这个任务。
对于给定的闭区间 [a,b] ,你要找出里面所有的等差数列,并输出所有的等差数列。
这里有一个要求,同一个数不能同时存在于两个等差数列中。
比如 a,b,c,d,e 中, a,b,c 是一个等差数列, c,d,e 也是一个等差数列,后一个等差数列就不能以 c 开始,所以 c,d,e 在本题不构成等差数列。
输入格式
输入占一行,只包含两个数 a 和 b ,并用空格隔开。
输出格式
输出占若干行,每行为一个等差数列,每个数用空格隔开。
样例输入输出
样例输入
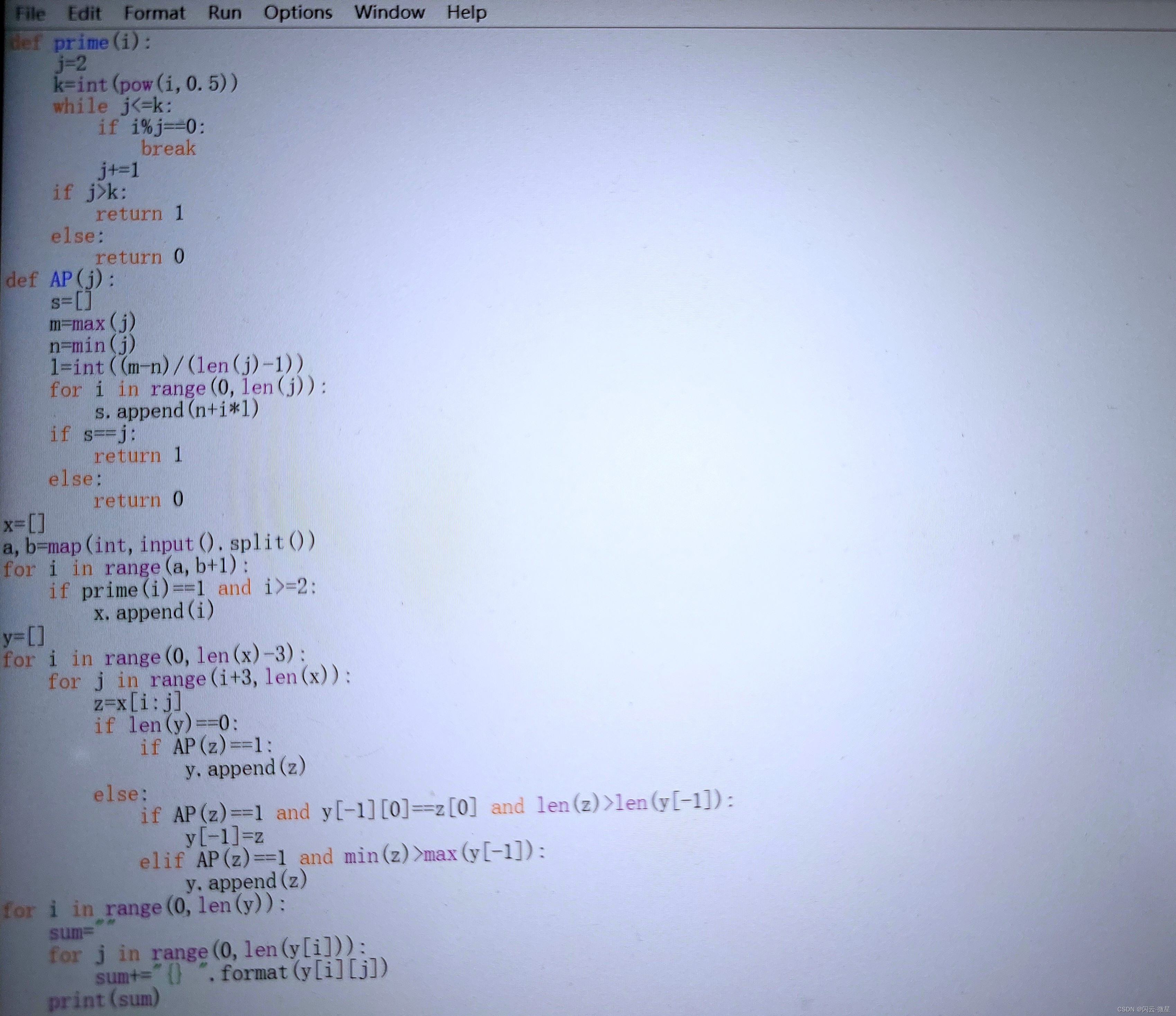
141 400
样例输出
151 157 163
167 173 179
199 211 223
251 257 263 269
367 373 379
数据范围
对于 100% 的数据,保证 a<b,a≤1000,b≤100000 。
来源/分类(难度系数:三星)
质数 模拟 NOIP普及组
完整代码展示:
def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k:
return 1
else:
return 0
def AP(j):
s=[]
m=max(j)
n=min(j)
l=int((m-n)/(len(j)-1))
for i in range(0,len(j)):
s.append(n+i*l)
if s==j:
return 1
else:
return 0
x=[]
a,b=map(int,input().split())
for i in range(a,b+1):
if prime(i)==1 and i>=2:
x.append(i)
y=[]
for i in range(0,len(x)-3):
for j in range(i+3,len(x)):
z=x[i:j]
if len(y)==0:
if AP(z)==1:
y.append(z)
else:
if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):
y[-1]=z
elif AP(z)==1 and min(z)>max(y[-1):
y.append(z)
for i in range(0,len(y)):
sum=""
for j in range(0,len(y[i])):
sum+="{} ".format(y[i][j])
print(sum)
def prime(i):j=2k=int(pow(i,0.5))while j<=k:if i%j==0:breakj+=1if j>k:return 1else:return 0
def AP(j):s=[]m=max(j)n=min(j)l=int((m-n)/(len(j)-1))for i in range(0,len(j)):s.append(n+i*l)if s==j:return 1else:return 0
x=[]
a,b=map(int,input().split())
for i in range(a,b+1):if prime(i)==1 and i>=2:x.append(i)
y=[]
for i in range(0,len(x)-3):for j in range(i+3,len(x)):#将i+3错误写为3,导致出现:ZeroDivisionErrorz=x[i:j]if len(y)==0:if AP(z)==1:y.append(z)else:if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):#尽可能地延长等差数列y[-1]=zelif AP(z)==1 and min(z)>max(y[-1]):#保证数列符合所给条件y.append(z)
for i in range(0,len(y)):sum=""for j in range(0,len(y[i])):sum+="{} ".format(y[i][j])print(sum)
代码解释:
“def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k:
return 1
else:
return 0 ”,根据素数的定义自定义一个函数prime(),用于判断prime()函数中实参是否为素数:如果是,则返回值1,否则返回值0。
“def AP(j):
s=[]
m=max(j)
n=min(j)
l=int((m-n)/(len(j)-1))
for i in range(0,len(j)):
s.append(n+i*l)
if s==j:
return 1
else:
return 0 ”,根据等差数列的定义自定义一个函数AP(),用于判断AP()中的实参是否为等差数列,如果是:则返回值1,否则返回值0。
“x=[]
a,b=map(int,input().split())
for i in range(a,b+1):
if prime(i)==1 and i>=2:
x.append(i) ”,建立一个空列表x,接着导入用户给定的闭区间[a,b]。遍历a~b的所有数字,将属于素数的数字添加进列表x中。
“y=[]
for i in range(0,len(x)-3):
for j in range(i+3,len(x)):
z=x[i:j]
if len(y)==0:
if AP(z)==1:
y.append(z)
else:
if AP(z)==1 and y[-1][0]==z[0] and len(z)>len(y[-1]):
y[-1]=z
elif AP(z)==1 and min(z)>max(y[-1]):#保证数列符合所给条件
y.append(z) ”,建立一个空列表y,接着遍历x中元素,按顺序截取元素个数大于等于三的数列。如果y列表为空,则将第一个符合等差数列的数列添加进y中;否则1:判断新查找得到的等差数列与y中的最后一个数列y[-1]是否有重复元素,如果没有,则将其添加进y中。2:判断新查找得到的等差数列的第一个元素与y中最后一个元素y[-1]的第一个元素相同且该数列的长度大于y[-1],如果是,则将该数列替换y[-1]。
“for i in range(0,len(y)):
sum=""
for j in range(0,len(y[i])):
sum+="{} ".format(y[i][j])
print(sum) ”,遍历y中元素:建立一个空字符串sum,sum依次连接y[i]中的元素,最终打印sum。
运行效果展示:
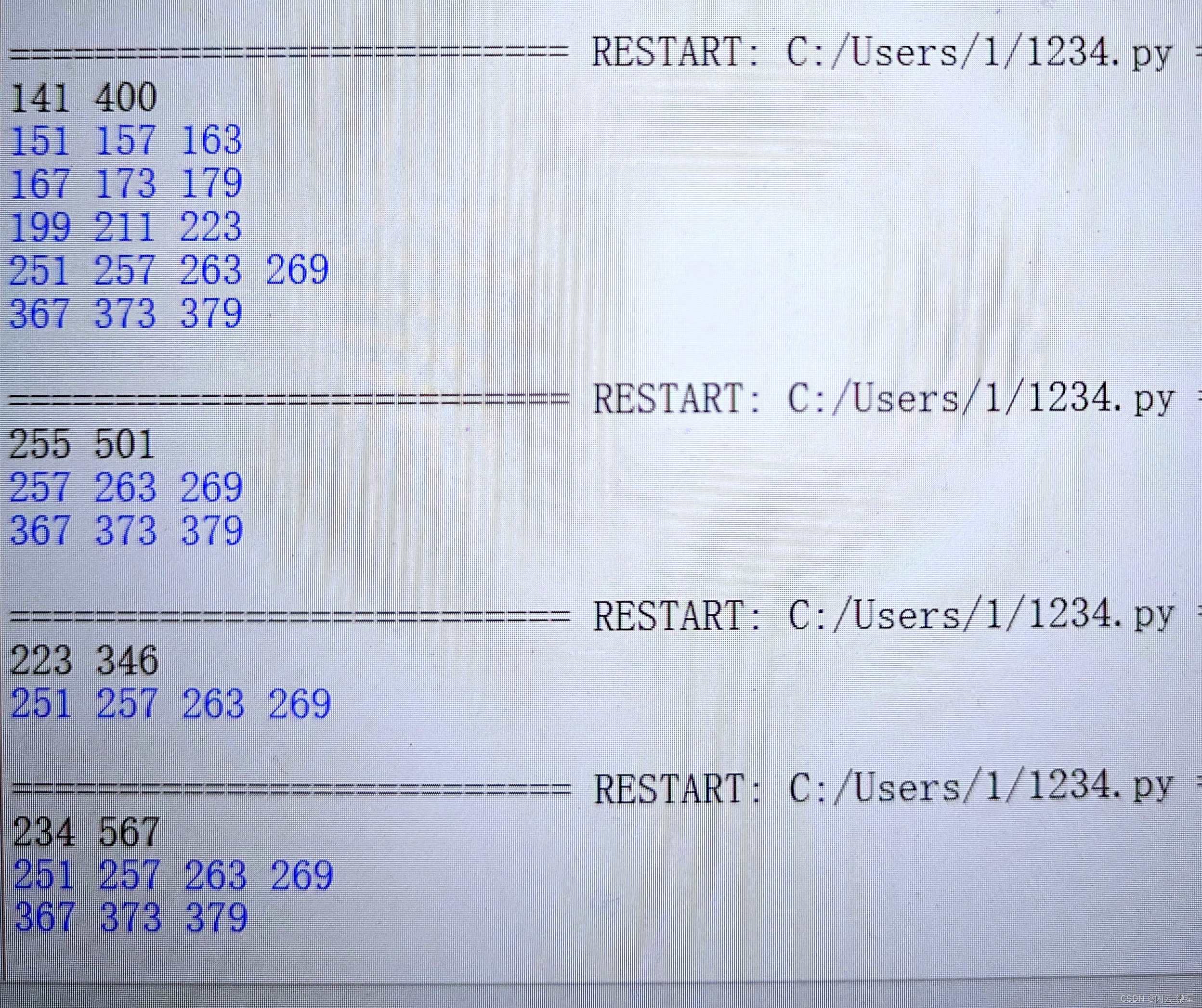
(声明:以上内容均为原创)
相关文章:

python-素数中的等差数列
题目描述 质数是在数论中很有意思的数,有很多题都可以围绕它来出,就如你眼前所见的这道题。 给定一个闭区间 [a,b] ,将此范围内的所有素数进行从小到大排序,对于连续的素数,我们可以发现很多等差数列(元素个数大于等于 3 )&#x…...

Unity3D 服务器AStar寻路客户端位置同步显示验证详解
在游戏开发中,经常需要在服务器和客户端之间同步玩家的位置信息,以便其他玩家可以看到他们的移动。本文将详细介绍如何在Unity 3D中使用AStar算法进行路径规划,并在服务器和客户端之间同步玩家的位置信息。 对惹,这里有一个游戏开…...

无人机之悬停精度篇
无人机的悬停精度是指无人机在无GPS信号或其他外部定位辅助下,能够保持在一个固定空间位置时的精度。这一精度受到多种因素的影响,包括但不限于风速、气压、温度、湿度以及无人机自身的姿态稳定性等。以下是对无人机悬停精度的详细分析: 一、…...

力扣题解2848
大家好,欢迎来到无限大的频道。 今日继续给大家带来力扣题解。 题目描述(简单): 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] &…...

电子电气架构---智能汽车应该是怎么样的架构?
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不…...

无心剑七绝《中秋相思》
七绝中秋相思 中秋月满意深长 百代江阳老窖香 莫道天涯情不尽 相思寸寸赋华章 2023年9月29日 平水韵七阳平韵 这首诗七绝《中秋相思》由无心剑所作,以其深情的笔触描绘了中秋夜的相思之情。 诗中首句“中秋月满意深长”即以中秋圆月为起点,勾勒出了一幅…...

Python画笔案例-051 绘制赵爽弦图
1、绘制赵爽弦图 通过 python 的turtle 库绘制 赵爽弦图,如下图: 2、实现代码 绘制 赵爽弦图,以下为实现代码: """赵爽弦图.py本程序演录了如何自定义形状,如何把它添加到造型字典。赵爽弦图是用来证明…...

SEGGERS实时系统embOS推出Linux端模拟器
SEGGER 发布了两个新的 embOS 仿真模拟器:embOS Sim Linux 和 embOS-MPU Sim Linux。 通过模拟 Linux 主机系统上的硬件,取代物理硬件,为开发人员提供了一种无缝的方式来构建原型和测试应用程序。 embOS Sim Linux 端口支持 32 位和 64 位系…...

HTML + CSS - 网页布局之一般布局浮动布局
1. 一般布局 1.1 一般布局相关参数 元素内容常常可以想像为放在一个盒子里,然后在周边加上内边距,边框和外边距,是盒子模型 默认一个块级区域会填充父类所有的行向空间,并且沿着块伸长容纳其内容,可以为块状体设置某…...

python定时任务,定时爬取水质和天气
定时爬取水质和天气 代码 代码 from apscheduler.schedulers.background import BackgroundScheduler import requests import datetimeurlweather "http://localhost:8000/CrwalingViewWeather" # 天气接口 urlwater "http://localhost:8000/CrwalingViewW…...

ARM驱动学习之基础小知识
ARM驱动学习之基础小知识 • sch原理图工程师工作内容 – 方案 – 元器件选型 – 采购(能不能买到,价格) – 原理图(涉及到稳定性) • layout画板工程师 – layout(封装、布局,布线,…...

【字幕】恋上数据结构与算法之019动态数组07打印数组
是吧?什么意思呢?你看啊我们刚刚已经加了三个东西了,我现在希望能够打印一下这个速度,希望能把它里面所有元素打出来,那我们试一下,看它默认是怎么打,这个时候我们右击你会发现它打出来长这样子…...

Python基础语法(3)下
列表和元组 列表是什么,元组是什么 编程中,经常需要使用变量,来保存/表示数据。变量就是内存空间,用来表示或者存储数据。 如果代码中需要表示的数据个数比较少,我们直接创建多个变量即可。 num1 10 num2 20 num3…...
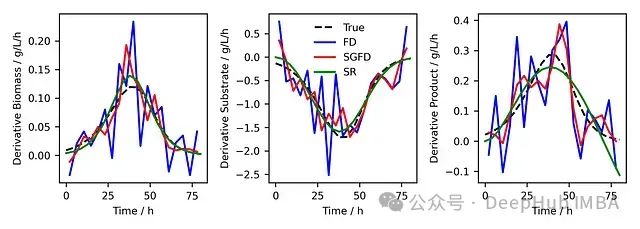
数据稀缺条件下的时间序列微分:符号回归(Symbolic Regression)方法介绍与Python示例
时间序列概况在日常生活和专业研究中都很常见。简而言之,时间序列概况是一系列连续的数据点 y(0), y(1), …, y(t) ,其中时间 t 的点依赖于时间 t-1 的前一个点(或更早的时间点)。 在许多应用中,研究者致力于预测时间序列概况的未来行为。存在各种建模方法。这些模型通常基于过…...
XML_Tomcat_HTTP
第四章 XML_Tomcat10_HTTP 一 XML XML是EXtensible Markup Language的缩写,翻译过来就是可扩展标记语言。所以很明显,XML和HTML一样都是标记语言,也就是说它们的基本语法都是标签。 可扩展 三个字表面上的意思是XML允许自定义格式。但这不代…...

GPT Prompt
Reference https://help.openai.com/en/articles/6654000-best-practices-for-prompt-engineering-with-the-openai-apihttps://platform.openai.com/docs/guides/prompt-engineeringbilibili 8分钟系统学习提示工程,别再说大模型还不够聪明!Prompt Engineering,提示词,Few…...

go基础知识归纳总结
无缓冲的 channel 和有缓冲的 channel 的区别? 在 Go 语言中,channel 是用来在 goroutines 之间传递数据的主要机制。它们有两种类型:无缓冲的 channel 和有缓冲的 channel。 无缓冲的 channel 行为:无缓冲的 channel 是一种同步…...

【字幕】恋上数据结构与算法之014动态数组02接口设计
申请表数组英文单词叫away,而这个数组是怎么样的申请表?数组是一种顺序存储的申请表,什么叫顺序存储?就是数组里面的所有元素,它的内存地址是连续的,大家的内存是连续的,比如说举个例子…...

ffmpeg硬件解码一般流程
流程 根据硬件名称,查询是否是支持的类型 const char *device_name "qsv"; //cuda enum AVHWDeviceType type av_hwdevice_find_type_by_name(device_name); if(type AV_HWDEVICE_TYPE_NONE) {//如果一个硬件类型是不支持的,打印所有支持…...

微信支付开发-程序开发
一、操作流程图 二、后端代码实现 1、题库实现 a、列表、所有、详情、保存、启禁用、导入答题 b、获取奖品信息、保存奖品信息、 class Question extends Base {// 列表public function getList(){$param $this->request->param();$where [];if(!empty($param[title])…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

年度峰会上,抖音依靠人工智能和搜索功能吸引广告主
上周早些时候举行的第五届年度TikTok World产品峰会上,TikTok推出了一系列旨在增强该应用对广告主吸引力的功能。 新产品列表的首位是TikTok Market Scope,这是一个全新的分析平台,为广告主提供整个考虑漏斗的全面视图,使他们能够…...
