补题篇--codeforces
传送门:Problem - 1881C - Codeforces
题目大意:

思路:
首先解决这个问题要知道 一个 ( x , y ) 顺时钟旋转 90 , 180 , 270可以得到 ( y , n - x + 1 ) ,
( n - x + 1 , n - y + 1 ) ,( n - y + 1 , x )
由于一个字符只能增大,所以可以找到旋转位置的最大字符,每个字符都要变成最大字符,因此求出答案
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{int n; cin >> n;vector<vector<char>> arr(n + 1, vector<char>(n + 1));for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++) cin >> arr[i][j];}int ans = 0;for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){int temp1 = max({ arr[i][j] , arr[j][n - i + 1] , arr[ n - j + 1 ][i] , arr[n - i + 1][n - j + 1] }) - 'a';int temp2 = arr[i][j] + arr[j][n - i + 1] + arr[n - j + 1][i] + arr[n - i + 1][n - j + 1] - 4 * 'a';ans += 4 * temp1 - temp2;}}cout << ans / 4 << endl;
}
signed main()
{int tt; cin >> tt;while (tt--)solve();return 0;
}传送门:Problem - 1879C - Codeforces
题目大意:

思路:
如何计算最小操作次数: 相同的区间段只能保留一个数字 00011101001111 -> 3 3 1 1 2 4
需要删除的数字个数 sum = ( len1 - 1 ) + ( len2 - 1 ) + ( len3 - 1 ) ......
如何计算最短操作序列的个数:C( len - 1 , len ) == len,一个区间段需要删除的数字序列是 len,
而这些数 ( sum )做全排列,sum的阶乘 答案就是 len * sum!
0110110001 -> 1 2 1 2 3 1 ->第一个序列不用删除,第二个序列 11 可以删除 2 个(第二个或第三个1) ,第三个序列不用删除,第四个序列删除 3 个 ,第五个序列不用删除,删除的这些数还有做全排列
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
const int mod = 998244353;
int f[N];
void solve()
{string s; cin >> s;int n = s.size();s = " " + s;int ans = 1;int sum = 0;int len = 1;for( int i = 2; i <= n; i++){if( s[i] != s[i-1] ) {ans = ans * len % mod ; sum += ( len - 1 ); len = 1;}else len++;}ans = ans * len % mod;sum += ( len - 1 );cout << sum << " " << ans * f[sum] % mod << endl;
}
signed main()
{f[0] = 1;for( int i = 1; i <= 2e5 ; i++ ) f[i] = f[i-1] * i % mod;// 预处理阶乘int tt; cin >> tt;while(tt--)solve();return 0;
}相关文章:

补题篇--codeforces
传送门:Problem - 1881C - Codeforces 题目大意: 思路: 首先解决这个问题要知道 一个 ( x , y ) 顺时钟旋转 90 , 180 , 270可以得到 ( y , n - x 1 ) , ( n - x 1 , n - y 1 ) ,( n - y …...

【字幕】恋上数据结构与算法之015动态数组03简单接口的实现
我们先来看一下,不要着急啊大家不要着急,这些东西我肯定会一点一点会给大家去实现,最终实现到跟Java官方版本差不多,只要我们自己实现了,偶尔类似的,你会发现你倒回去看Java官方的那个源码,你会…...

基于2023年网络赛赛题了解OpenCv
一、OpenCv图像读取与显示 1.图像的读取与显示 cv.imread() 图像读取,第一个参数是照片的位置一般是完整路径,第二个参数是指定图片输出的样式 cv.IMREAD_COLOR: 加载彩色图像。任何图像的透明度都会被忽视。(默认模式)。cv.I…...

你到底更适合买虚拟主机还是服务器?
前言 在当今数字化的时代,选择合适的网络服务平台对于个人和企业来说至关重要。无论是搭建个人博客、运营企业网站还是开发游戏,服务器的选择都会直接影响到项目的成本、性能以及用户体验。那么,你到底适合虚拟主机还是服务器呢?…...

linux手册翻译 addr2line
名称 addr2line 将地址转换为文件名和代码行数 简介 addr2line [-a|--addresses][-b bfdname|--targetbfdname][-C|--demangle[style]][-r|--no-recurse-limit][-R|--recurse-limit][-e filename|--exefilename][-f|--functions] [-s|--basename][-i|--inlines][-p|--pretty-…...
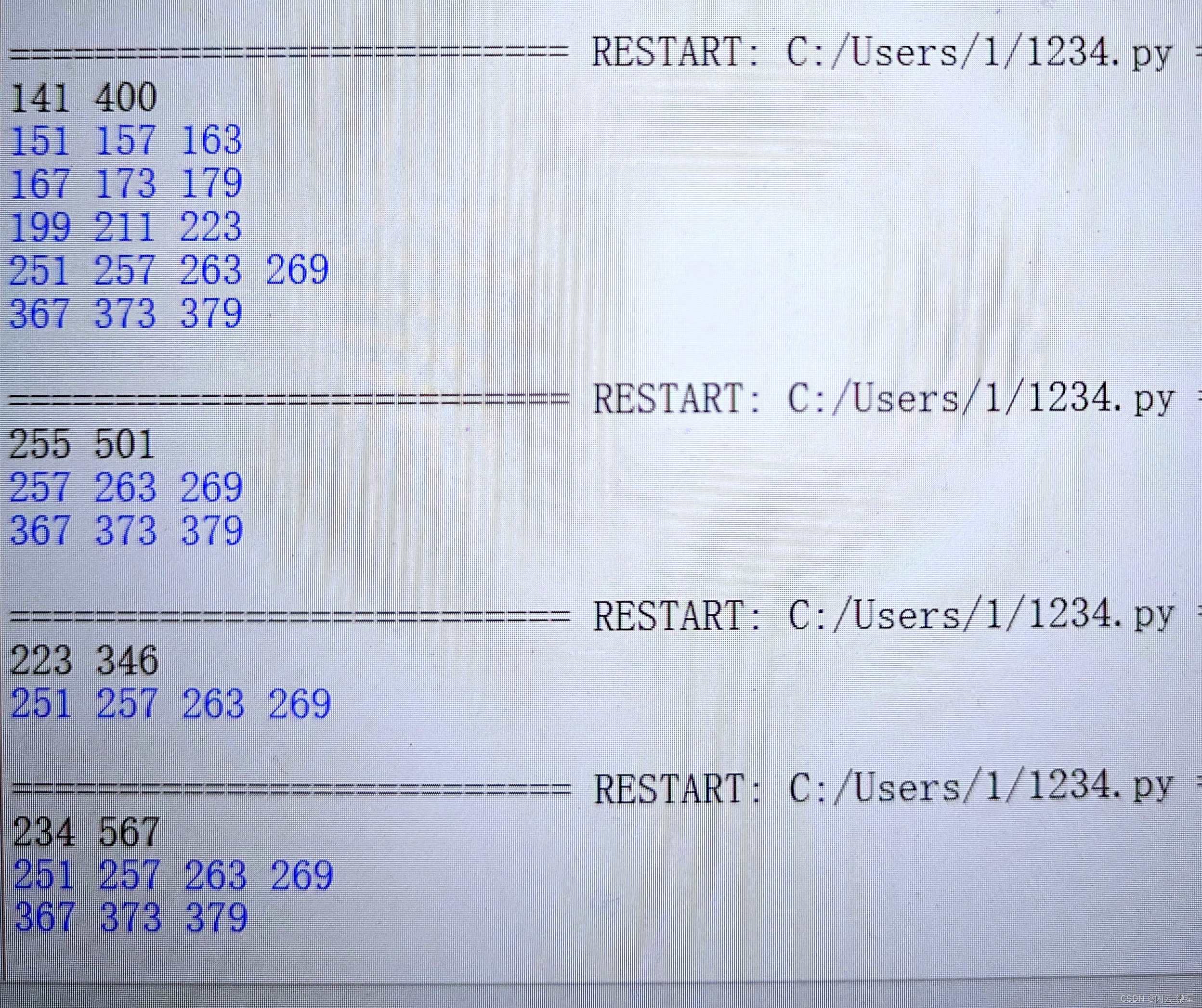
python-素数中的等差数列
题目描述 质数是在数论中很有意思的数,有很多题都可以围绕它来出,就如你眼前所见的这道题。 给定一个闭区间 [a,b] ,将此范围内的所有素数进行从小到大排序,对于连续的素数,我们可以发现很多等差数列(元素个数大于等于 3 )&#x…...

Unity3D 服务器AStar寻路客户端位置同步显示验证详解
在游戏开发中,经常需要在服务器和客户端之间同步玩家的位置信息,以便其他玩家可以看到他们的移动。本文将详细介绍如何在Unity 3D中使用AStar算法进行路径规划,并在服务器和客户端之间同步玩家的位置信息。 对惹,这里有一个游戏开…...

无人机之悬停精度篇
无人机的悬停精度是指无人机在无GPS信号或其他外部定位辅助下,能够保持在一个固定空间位置时的精度。这一精度受到多种因素的影响,包括但不限于风速、气压、温度、湿度以及无人机自身的姿态稳定性等。以下是对无人机悬停精度的详细分析: 一、…...

力扣题解2848
大家好,欢迎来到无限大的频道。 今日继续给大家带来力扣题解。 题目描述(简单): 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] &…...

电子电气架构---智能汽车应该是怎么样的架构?
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不…...

无心剑七绝《中秋相思》
七绝中秋相思 中秋月满意深长 百代江阳老窖香 莫道天涯情不尽 相思寸寸赋华章 2023年9月29日 平水韵七阳平韵 这首诗七绝《中秋相思》由无心剑所作,以其深情的笔触描绘了中秋夜的相思之情。 诗中首句“中秋月满意深长”即以中秋圆月为起点,勾勒出了一幅…...

Python画笔案例-051 绘制赵爽弦图
1、绘制赵爽弦图 通过 python 的turtle 库绘制 赵爽弦图,如下图: 2、实现代码 绘制 赵爽弦图,以下为实现代码: """赵爽弦图.py本程序演录了如何自定义形状,如何把它添加到造型字典。赵爽弦图是用来证明…...

SEGGERS实时系统embOS推出Linux端模拟器
SEGGER 发布了两个新的 embOS 仿真模拟器:embOS Sim Linux 和 embOS-MPU Sim Linux。 通过模拟 Linux 主机系统上的硬件,取代物理硬件,为开发人员提供了一种无缝的方式来构建原型和测试应用程序。 embOS Sim Linux 端口支持 32 位和 64 位系…...

HTML + CSS - 网页布局之一般布局浮动布局
1. 一般布局 1.1 一般布局相关参数 元素内容常常可以想像为放在一个盒子里,然后在周边加上内边距,边框和外边距,是盒子模型 默认一个块级区域会填充父类所有的行向空间,并且沿着块伸长容纳其内容,可以为块状体设置某…...

python定时任务,定时爬取水质和天气
定时爬取水质和天气 代码 代码 from apscheduler.schedulers.background import BackgroundScheduler import requests import datetimeurlweather "http://localhost:8000/CrwalingViewWeather" # 天气接口 urlwater "http://localhost:8000/CrwalingViewW…...

ARM驱动学习之基础小知识
ARM驱动学习之基础小知识 • sch原理图工程师工作内容 – 方案 – 元器件选型 – 采购(能不能买到,价格) – 原理图(涉及到稳定性) • layout画板工程师 – layout(封装、布局,布线,…...

【字幕】恋上数据结构与算法之019动态数组07打印数组
是吧?什么意思呢?你看啊我们刚刚已经加了三个东西了,我现在希望能够打印一下这个速度,希望能把它里面所有元素打出来,那我们试一下,看它默认是怎么打,这个时候我们右击你会发现它打出来长这样子…...

Python基础语法(3)下
列表和元组 列表是什么,元组是什么 编程中,经常需要使用变量,来保存/表示数据。变量就是内存空间,用来表示或者存储数据。 如果代码中需要表示的数据个数比较少,我们直接创建多个变量即可。 num1 10 num2 20 num3…...
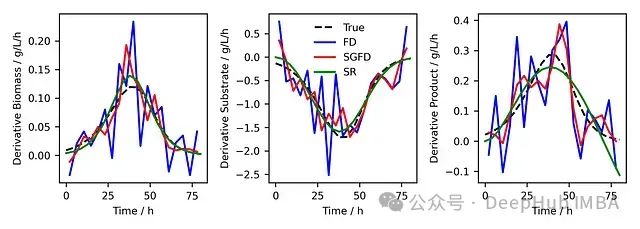
数据稀缺条件下的时间序列微分:符号回归(Symbolic Regression)方法介绍与Python示例
时间序列概况在日常生活和专业研究中都很常见。简而言之,时间序列概况是一系列连续的数据点 y(0), y(1), …, y(t) ,其中时间 t 的点依赖于时间 t-1 的前一个点(或更早的时间点)。 在许多应用中,研究者致力于预测时间序列概况的未来行为。存在各种建模方法。这些模型通常基于过…...
XML_Tomcat_HTTP
第四章 XML_Tomcat10_HTTP 一 XML XML是EXtensible Markup Language的缩写,翻译过来就是可扩展标记语言。所以很明显,XML和HTML一样都是标记语言,也就是说它们的基本语法都是标签。 可扩展 三个字表面上的意思是XML允许自定义格式。但这不代…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
