06_Python数据类型_元组

Python的基础数据类型
- 数值类型:整数、浮点数、复数、布尔
- 字符串
- 容器类型:列表、元祖、字典、集合
元组
- 元组(Tuple)是一种不可变的序列类型,与列表类似,但有一些关键的区别。
- 本质:只读的列表(list)
定义元组
元组是由圆括号 () 包围的元素集合,元素之间用逗号分隔。元组一旦创建,其内容不能被修改。
# 创建一个空元组
empty_tuple = ()# 创建一个包含几个元素的元组
my_tuple = (1, 2, 3, 'a', 'b', 'c')
访问元组元素
与列表一样,元组中的元素是有序的,可以通过索引来访问。
# 访问第一个元素
first_element = my_tuple[0] # 结果是 1
print(first_element)
# 访问最后一个元素
last_element = my_tuple[-1] # 结果是 'c'
print(last_element)
元组切片
元组也支持切片操作。
# 获取从索引1到索引3(不包括索引3)的元素
sub_tuple = my_tuple[1:4] # 结果是 (2, 3, 'a')
print(sub_tuple)
元组不可变性
元组是不可变的,这意味着你不能修改元组中的元素。
# 尝试修改元组中的元素会导致TypeError
# my_tuple[0] = 'one' # 这行代码会抛出错误
元组与列表的转换
可以使用 tuple() 函数将列表转换为元组,使用 list() 函数将元组转换为列表。
# 将列表转换为元组
my_list = [1, 2, 3]
my_tuple = tuple(my_list)
print(my_tuple)
# 将元组转换为列表
my_list_again = list(my_tuple)
print(my_list_again)
元组的优势
尽管元组是不可变的,但它们在以下情况下非常有用:
- 当你需要确保数据不会被意外修改时。
- 当你需要一个不可变的序列作为字典的键时。
- 当你从函数返回多个值时。
元组运算符
元组支持以下运算符:
- 索引运算符 []
- 切片运算符 [:]
- 成员运算符 in 和 not in
- 身份运算符 is 和 is not
元组与浅拷贝、深拷贝
由于元组是不可变的,通常不需要对元组进行浅拷贝或深拷贝。当你尝试对元组进行浅拷贝或深拷贝时,实际上会返回元组本身,因为它的内容无法改变。
import copy# 浅拷贝和深拷贝元组
my_tuple = (1, 2, 3)
shallow_copied_tuple = copy.copy(my_tuple) # 返回元组本身
deep_copied_tuple = copy.deepcopy(my_tuple) # 也返回元组本身
# 在这里,shallow_copied_tuple 和 deep_copied_tuple 都是 my_tuple 的引用,因为元组不可变,所以没有必要创建副本。
print(id(shallow_copied_tuple))
print(id(deep_copied_tuple))
附件
本文对应的jupyter notebook源码链接,欢迎下载练习:https://download.csdn.net/download/fx_yzjy101/89757860
如有问题请留言。
相关文章:

06_Python数据类型_元组
Python的基础数据类型 数值类型:整数、浮点数、复数、布尔字符串容器类型:列表、元祖、字典、集合 元组 元组(Tuple)是一种不可变的序列类型,与列表类似,但有一些关键的区别。本质:只读的列表…...

【Vue】- ref获取DOM元素和购物车案例分析
文章目录 知识回顾前言源码分析1. ref2. 购物车案例分析3. 购物车计算、全选 拓展知识数据持久化localStorage 总结 知识回顾 前言 元素上使用 ref属性关联响应式数据,获取DOM元素 步骤 ● 创建 ref > const hRef ref(null) ● 模板中建立关联 > <h1 re…...

【AI大模型】ChatGPT模型原理介绍(下)
目录 🍔 GPT-3介绍 1.1 GPT-3模型架构 1.2 GPT-3训练核心思想 1.3 GPT-3数据集 1.4 GPT-3模型的特点 1.5 GPT-3模型总结 🍔 ChatGPT介绍 2.1 ChatGPT原理 2.2 什么是强化学习 2.3 ChatGPT强化学习步骤 2.4 监督调优模型 2.5 训练奖励模型 2.…...

Python数据分析与可视化实战指南
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。 一、环境准…...

react18基础教程系列-- 框架基础理论知识mvc/jsx/createRoot
react的设计模式 React 是 mvc 体系,vue 是 mvvm 体系 mvc: model(数据)-view(视图)-controller(控制器) 我们需要按照专业的语法去构建 app 页面,react 使用的是 jsx 语法构建数据层,需要动态处理的的数据都要数据层支持控制层: 当我们需要…...
)
牛客周赛 Round 60 折返跑(组合数学)
题目链接:题目 大意: 在 1 1 1到 n n n之间往返跑m趟,推 m − 1 m-1 m−1次杆子,每次都向中间推,不能推零次,问有多少种推法(mod 1e97)。 思路: 一个高中学过的组合数…...

深入浅出Java匿名内部类:用法详解与实例演示
匿名内部类(Anonymous Inner Class)在Java中是一种非常有用的特性,它允许你在一个类的定义中直接创建并实例化一个内部类,而不需要为这个内部类指定一个名字。匿名内部类通常用于以下几种情况: 实现接口:当…...

数据库MySQL、Mariadb、PostgreSQL、MangoDB、Memcached和Redis详细介绍
以下是一些常见的后端开发数据库选型: 关系型数据库(RDBMS):关系型数据库是最常见的数据库类型,使用表格和关系模型来存储和管理数据。常见的关系型数据库包括MySQL、PostgreSQL和Oracle等。这些数据库适合处理结构化数…...

【ArcGIS Pro实操第七期】栅格数据合并、裁剪及统计:以全球不透水面积为例
【ArcGIS Pro实操第七期】批量裁剪:以全球不透水面积为例 准备:数据下载ArcGIS Pro批量裁剪数据集1 数据拼接2 数据裁剪3 数据统计:各栅格取值3.1 栅格计算器-精确提取-栅格数据特定值3.2 数据统计 4 不透水面积变化分析 参考 准备࿱…...

【Linux】Image、zImage与uImage的区别
1、Image 1.1 什么是 Image Image 是一种未压缩的 Linux 内核镜像文件,包含了内核的所有代码、数据和必要的元信息。它是 Linux 内核在编译过程中生成的一个原始的二进制文件,未经过任何压缩或额外的封装处理。由于未压缩,Image 文件相对较…...
:自定义cuda扩展)
算子加速(3):自定义cuda扩展
需要自定义某个层,或有时候用c++实现你的操作(c++扩展)可能会更好: 例如:需要实现一个新型的激活函数例如: bevfusion用cuda实现bevpool加速自定义扩展的步骤 (1) 首先用纯pytorch和python 实现我们所需的功能,看看效果再决定要不要进一步优化(2) 明确优化方向,用C++ (或CU…...

信息安全数学基础(14)欧拉函数
前言 在信息安全数学基础中,欧拉函数(Eulers Totient Function)是一个非常重要的概念,它与模运算、剩余类、简化剩余系以及密码学中的许多应用紧密相关。欧拉函数用符号 φ(n) 表示,其中 n 是一个正整数。 一、定义 欧…...

7-17 汉诺塔的非递归实现
输入样例: 3输出样例: a -> c a -> b c -> b a -> c b -> a b -> c a -> c 分析: 不会汉罗塔的uu们,先看看图解: 非递归代码: #include<iostream> #include<stack> using namespace std; s…...

word文档无损原样转pdf在windows平台使用python调用win32com使用pip安装pywin32
前提: windows环境下,并且安装了office套装,比如word,如果需要调用excel.也需要安装。在另外的文章会介绍。这种是直接调用word的。所以还原度会比较高。 需求: word文档转pdf,要求使用命令行形式,最终发布为api接口…...

海康威视相机在QTcreate上的使用教程
文章目录 前言:基础夯实:效果展示:图片展示:视频展示: 参考的资料:遇到问题:问题1:int64 does not问题2:LNK2019配置思路(这个很重要)配置关键图片:配置具体过…...
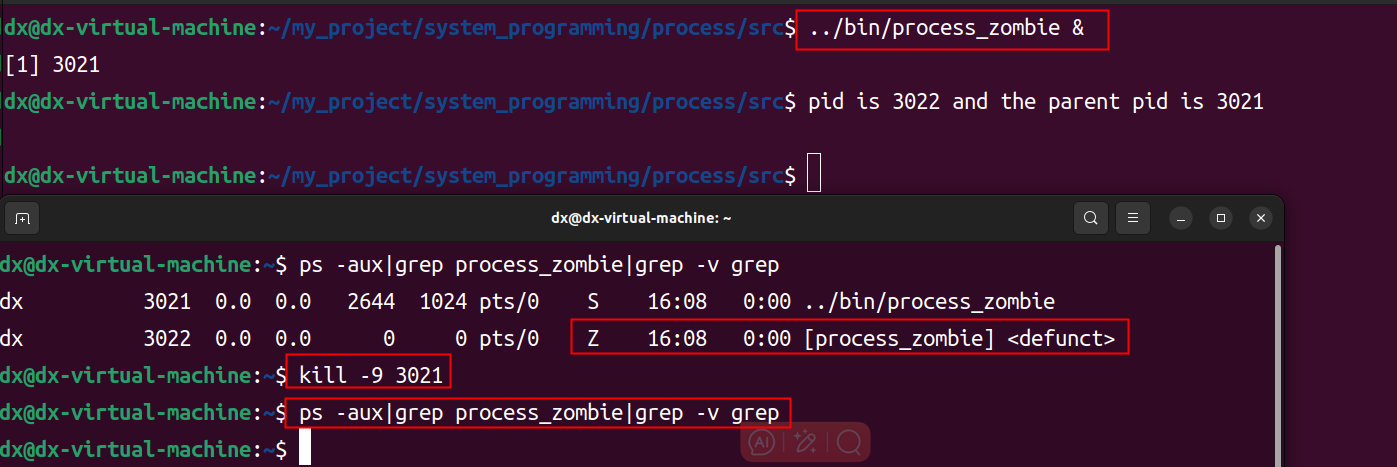
进程状态、进程创建和进程分类
文章目录 进程进程常见的状态进程调度进程状态变化关系 进程标识示例--进程标识的使用以及简介 进程创建fork函数vfork函数示例--使用fork函数创建子进程,并了解进程之间的关系 创建进程时发生的变化虚拟内存空间的变化示例--验证fork函数创建进程时的操作 对文件IO…...

java后端请求调用三方接口
java后端请求调用三方接口 /*** param serverURL http接口地址(例:http://www.iwsu.top:8016/dataSyn/bay/statsCar)* param parm 参数(可以是json,也可以是json数组)*/ public void doRestfulPostBody(St…...
)
C#使用TCP-S7协议读写西门子PLC(三)
接上篇 C#使用TCP-S7协议读写西门子PLC(二)-CSDN博客 这里我们进行封装读写西门子PLC的S7协议命令以及连接西门子PLC并两次握手 新建部分类文件SiemensS7ProtocolUtil.ReadWrite.cs 主要方法: 连接西门子PLC并发送两次握手。两次握手成功后,才真正连…...

铝型材及其常用紧固件、连接件介绍
铝型材介绍(包括紧固件和连接件以及走线) 铝型材 铝型材一般是6063铝合金挤压成型,分为欧标和国标两个标准。(左边国标,右边欧标,欧标槽宽一点) 由于槽型不一样,相关的螺栓和螺母也…...
-安装开发所需工具)
【裸机装机系列】7.kali(ubuntu)-安装开发所需工具
如果你是后端或是人工智能AI岗,可以安装以下推荐的软件: 1> sublime sublime官网 下载deb文件 安装命令 sudo dpkg -i sublime-text_build-4143_amd64.deb2> vscode 安装前置软件 sudo apt install curl gpg software-properties-common apt-t…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
