【学习笔记】「NOI2018」冒泡排序
从题解的角度来说,这是一道简单题。不过考场上在没有任何人提示的情况下要想出正确的结论其实并不容易。
我自己做这道题的时候,因为没有想清楚题目给出的下界能取到的充要条件是什么,所以到了很晚才猜到结论,以至于难以为继。
结论:当且仅当一个排列不含有长度为333的下降子序列,冒泡排序的交换次数取到下界。这也非常好理解,因为如果一个位置存在前面一个数比它大,后面一个数比它小,那么至少会向左/向右移动一次,因此取不到下界。
证明需要运用Dilworth\text{Dilworth}Dilworth定理,我们可以把原序列划分成两个上升子序列 ,其中一个子序列的数只会往左移,另一个子序列的数只会往右移,然后就证完了。
先不考虑字典序的限制。我们将限制转化一下,变成不存在一个位置iii,使得存在前面的一个数比它大,后面的一个数比它小。这直接导出了下面的dpdpdp:设dpi,jdp_{i,j}dpi,j表示前iii个位置,最大值为jjj的方案数。如果[1:i−1][1:i-1][1:i−1]的最大值为jjj,那么pip_ipi只能是[1:j][1:j][1:j]中没填的最小的那一个,方案数dpi−1,jdp_{i-1,j}dpi−1,j。否则,若[1:i−1][1:i-1][1:i−1]最大值为k(k<j)k(k<j)k(k<j),那么pip_ipi填jjj总是合法的。那么,dpi,j=∑k≤jdpi−1,k(i≤j)dp_{i,j}=\sum_{k\le j}dp_{i-1,k}(i\le j)dpi,j=∑k≤jdpi−1,k(i≤j) 。我们发现这就是从(1,1)(1,1)(1,1)走到(n,n)(n,n)(n,n)且不穿过对角线x=yx=yx=y的方案数,也就是(2nn)−(2nn−1)\binom{2n}{n}-\binom{2n}{n-1}(n2n)−(n−12n)。
回到原题,我们枚举lcp\text{lcp}lcp,然后就变成了求从(i,j)(i,j)(i,j)走到(n,n)(n,n)(n,n)的方案数,同样可以组合数计算。然后就做完了。
复杂度O(n)O(n)O(n)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int mod=998244353;
const int N=2e6+5;
int T,n,p[N],vs[N];
ll fac[N],inv[N],bit[N],res;
void add(ll &x,ll y){x=(x+y)%mod;
}
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
void init(int n){fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;inv[n]=fpow(fac[n]);for(int i=n;i>=1;i--)inv[i-1]=inv[i]*i%mod;
}
ll binom(ll x,ll y){return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
ll G(int a,int b,int c,int d){if(c>=a&&d>=b)return binom(c+d-a-b,c-a);return 0;
}
ll F(int a,int b,int c,int d){if(c>=a&&d>=b&&b>=a){return G(a,b,c,d)-G(b+1,a-1,c,d);}return 0;
}
int main(){ ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);init(2e6);cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>p[i],vs[i]=0;res=0;int tp=0,j=1;for(int i=0;i<n;i++){add(res,F(i,max(tp,p[i+1])+1,n,n));while(j<=n&&vs[j])j++;if(j<tp&&j>p[i+1]){add(res,F(i+1,tp,n,n));}if(p[i+1]<tp&&p[i+1]!=j){break;}tp=max(tp,p[i+1]);vs[p[i+1]]=1;}cout<<(res+mod)%mod<<"\n";}
}相关文章:

【学习笔记】「NOI2018」冒泡排序
从题解的角度来说,这是一道简单题。不过考场上在没有任何人提示的情况下要想出正确的结论其实并不容易。 我自己做这道题的时候,因为没有想清楚题目给出的下界能取到的充要条件是什么,所以到了很晚才猜到结论,以至于难以为继。 …...
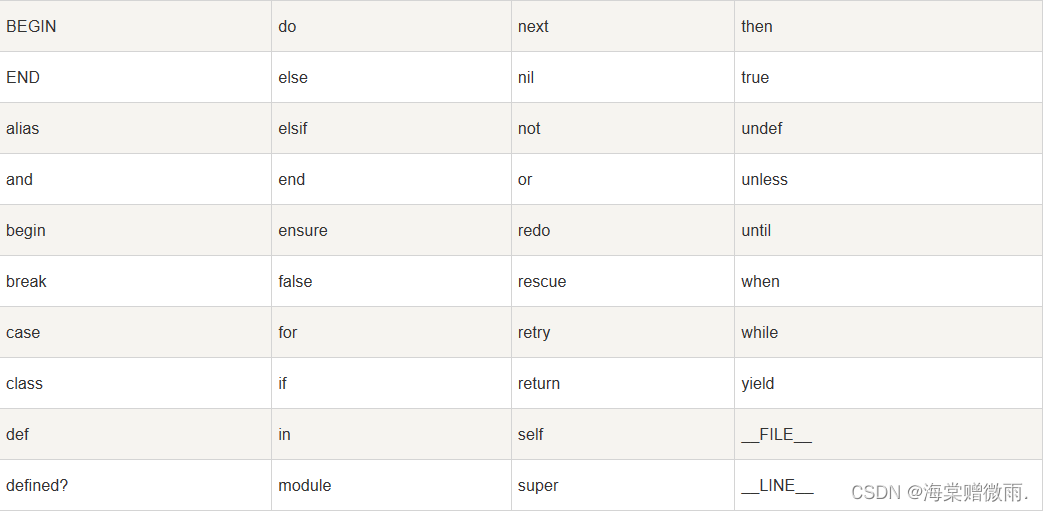
【Ruby学习笔记】3.Ruby 语法及数据类型
前言 本章介绍Ruby的语法和数据类型。 Ruby 语法 让我们编写一个简单的 Ruby 程序。所有的 Ruby 文件扩展名都是 .rb。所以,把下面的源代码放在 test.rb 文件中。 实例 #!/usr/bin/ruby -wputs "Hello, Ruby!";在这里,假设您的 /usr/bin …...

华为OD机试题【字符匹配】用 Java 解 | 含解题说明
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典本篇题目:字符匹配 题目 给你一个字符串…...
实现对象深拷贝的方法(5种))
JavaScript数组对象的浅拷贝与深拷贝(二)实现对象深拷贝的方法(5种)
JavaScript实现对象深拷贝的方法(5种)知识回调(不懂就看这儿!)场景复现实现对象深拷贝的五种方法1.json暴力转化2.es6扩展运算符3.for in循环遍历对象4.Object.assign()对象的合并5.利用循环和递归的方式实现对象浅拷贝…...

iPhone屏幕适配(之屏幕尺寸)
Device screen size 各设备屏幕尺寸 DeviceDimensions (portrait)iPhone 14 Pro Max430x932 pt (1290x2796 px 3x)iPhone 14 Pro393x852 pt (1179x2556 px 3x)iPhone 14 Plus428x926 pt (1284x2778 px 3x)iPhone 14390x844 pt (1170x2532 px 3x)iPhone 13 Pro Max428x926 pt (…...
手机变砖修复神器之 8 个的 Android手机系统修复工具
如果您经常在 Android 设备上遇到问题,则需要找到最好的 Android 系统修复应用程序并使用它来一劳永逸地解决您的问题。如果您不确定执行此操作的好应用是什么,我们在这里为您列出了一些最好的 Android 修复软件。 虽然现在出货的 Android 手机相当稳定…...
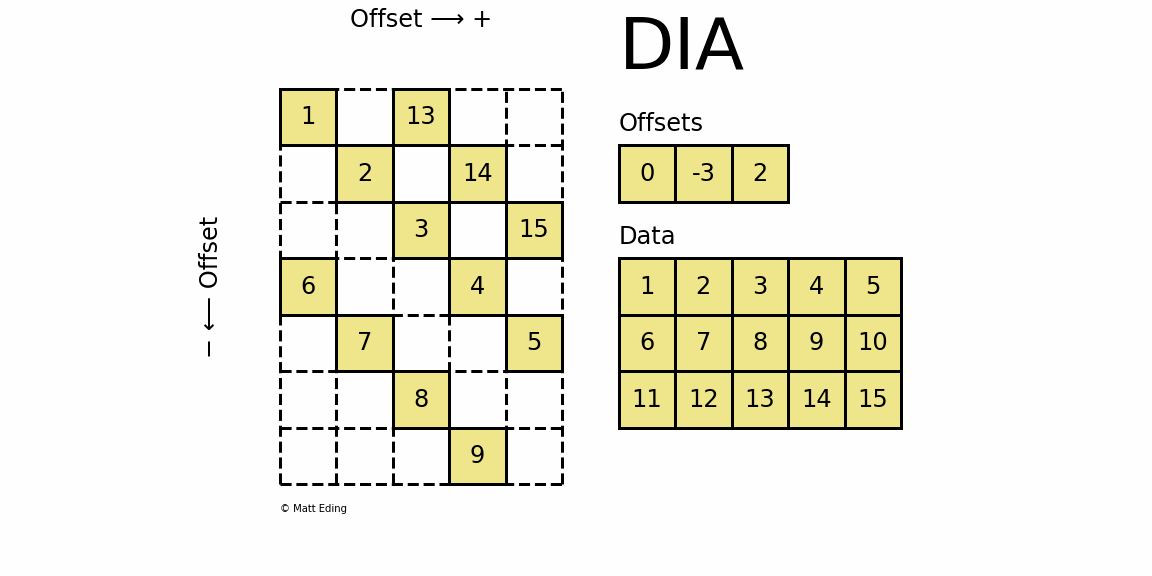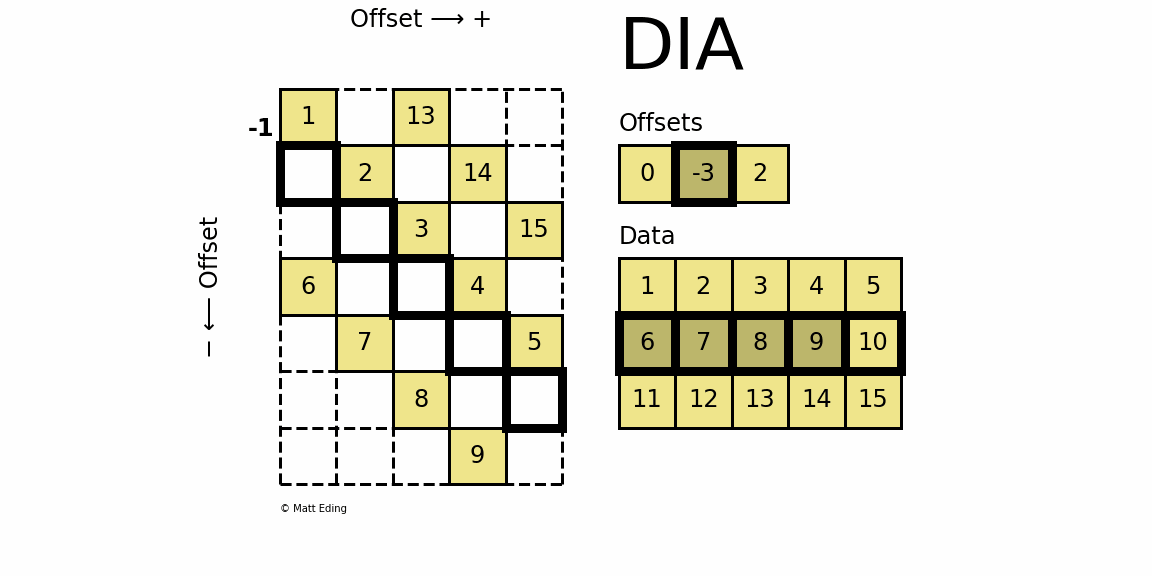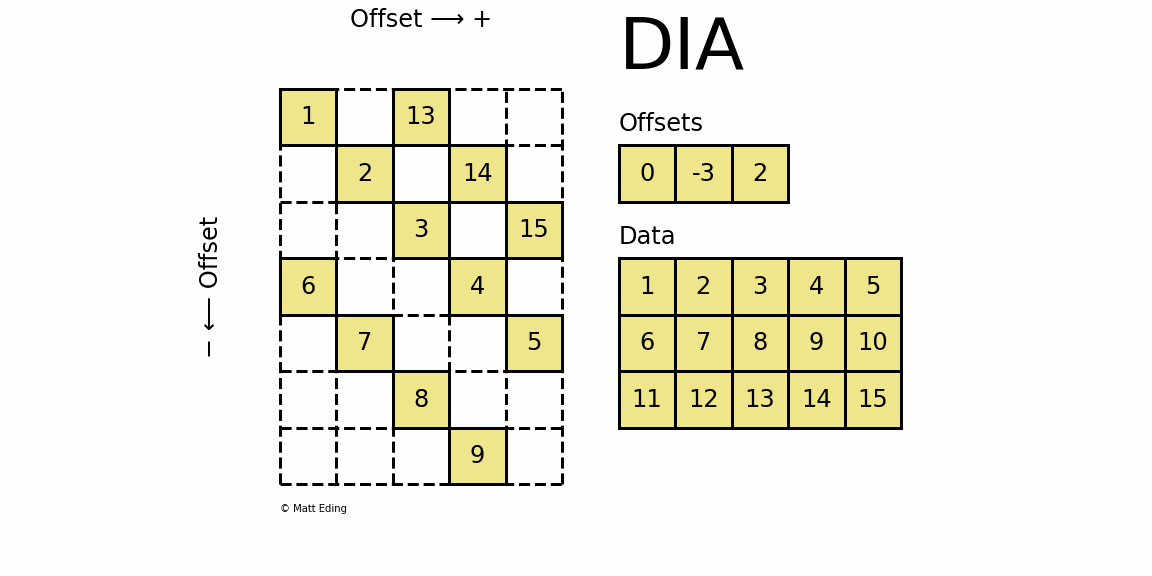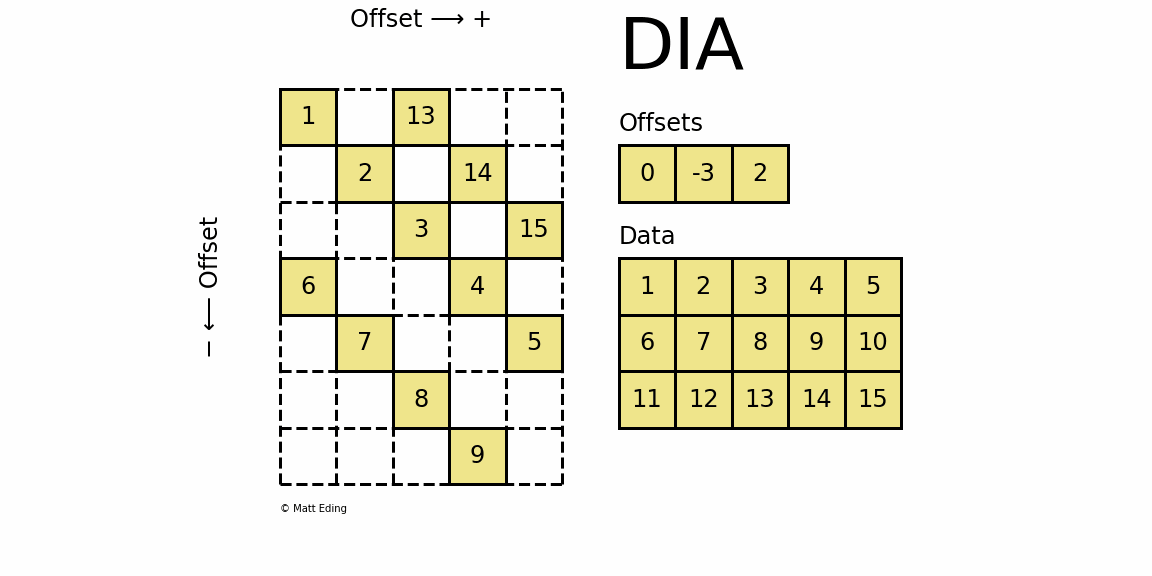
稀疏矩阵(Sparse Matrix)
1.背景 在数据科学和深度学习等领域常会采用矩阵格式来存储数据,但当矩阵较为庞大且非零元素较少时, 如果依然使用dense的矩阵进行存储和计算将是极其低效且耗费资源的。所以,通常我们采用Sparse稀疏矩阵的方式来存储矩阵,提高存储…...

深度学习中的损失函数
文章目录一. Loss函数1. 均方差损失(Mean Squared Error Loss)2. 平均绝对误差损失(Mean Absolute Error Loss)3.(Huber Loss)4. 分位数损失(Quantile Loss)5. 交叉熵损失࿰…...

English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [ð] Day29 2023.3.21 周二
English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [] Day29 2023.3.21 周二💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [θ]…...

【原始者-综述】
目录知识框架No.1 AcwingNo.2 LeetcodeNo.3 PTANo.4 蓝桥No.5 牛客网No.6 代码随想录知识框架 No.1 Acwing 那就点击这里转向自己的Acwing题解咯 单调栈,动态规划,贪心,回溯,二叉树,站与队列,双指针&#…...

C++内存模型
目录 一.内存分区 二,分区顺序 1 程序运行前 2 程序运行后 3.new操作符 一.内存分区 内存分区意义:不同区域存放的数据,赋予不同的生命周期, 给我们更大的灵活编程 内存可以分为以下几个区: 代码区:存放函数体的二进制代码…...
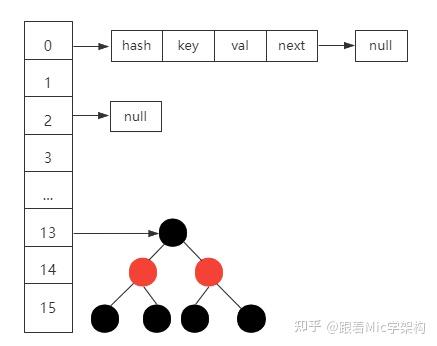
八股+面经
文章目录项目介绍Java基础MapHashMap v.s Hashtable(5点)ConcurrentHashMap v.s Hashtable(2点)代理模式1. 静态代理2. 动态代理2.1 JDK 动态代理机制2.2 CGLIB 动态代理机制Java并发线程volatilesynchronized线程池JVM类加载机制垃圾回收(GC)1. 引用类型…...
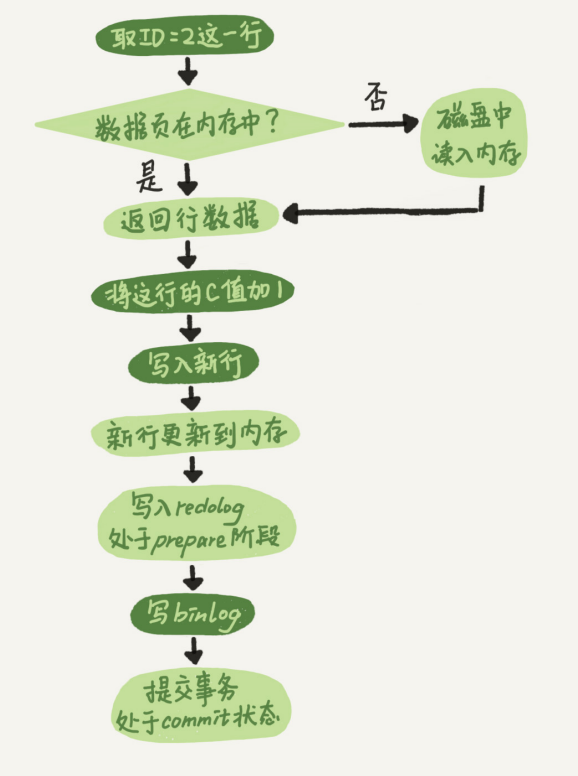
MySQL更新数据流程
1.mysql三种重要日志 redo log(重做日志):存在于引擎层,物理存储,通过设置innodb_flush_log_at_trx_xommit1 让其持久化到磁盘,保证引擎的crash-safe能力,遵从WAL技术(Write-Ahead …...
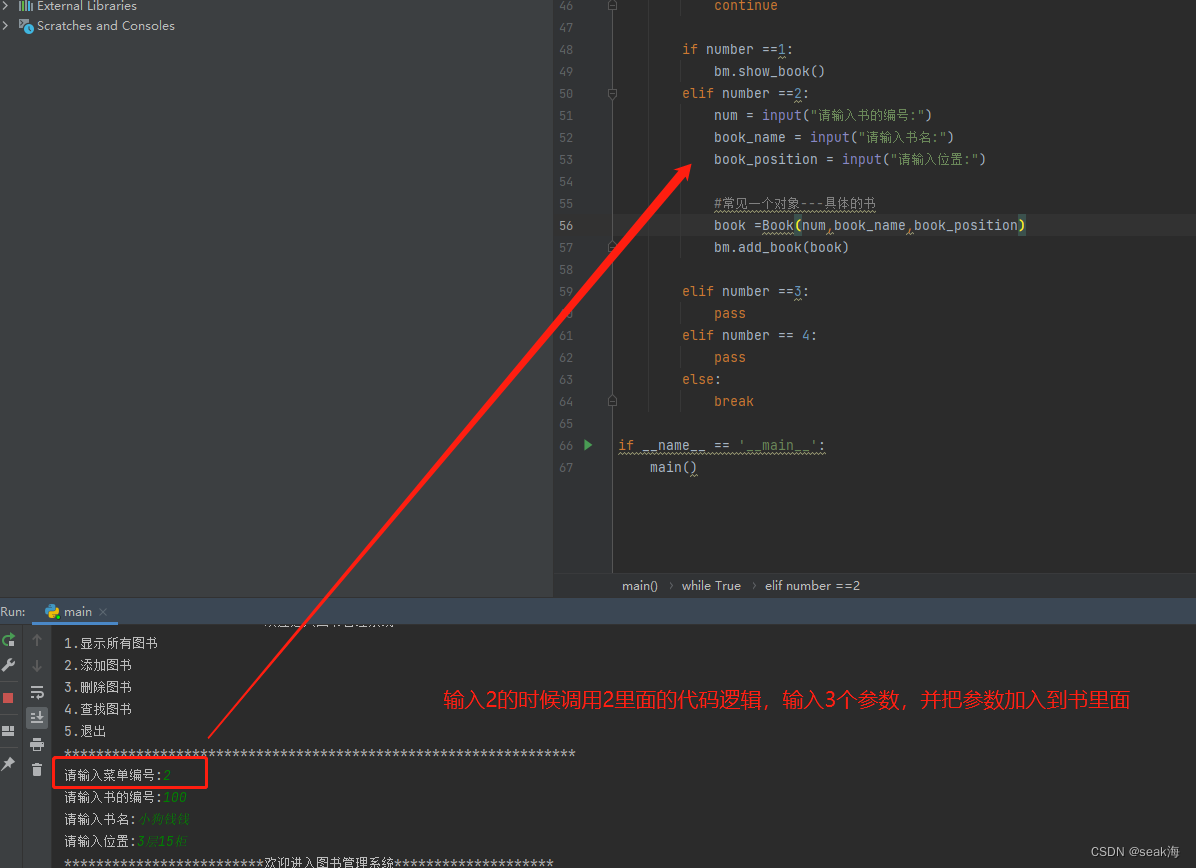
测试开发进阶系列课程
测试开发系列课程1.完善程序思维--------案列:图书管理系统的创建**(一)图书管理系统的创建**1.完善程序思维--------案列:图书管理系统的创建 (一)图书管理系统的创建 1.在main中写入主函数,…...
 对象树管理)
Qt源码阅读(三) 对象树管理
对象树管理 个人经验总结,如有错误或遗漏,欢迎各位大佬指正 😃 文章目录对象树管理设置父对象的作用设置父对象(setParent)完整源码片段分析对象的删除夹带私货时间设置父对象的作用 众所周知,Qt中,有为对象设置父对象…...
【Python入门第四十二天】Python丨NumPy 数组裁切
裁切数组 python 中裁切的意思是将元素从一个给定的索引带到另一个给定的索引。 我们像这样传递切片而不是索引:[start:end]。 我们还可以定义步长,如下所示:[start:end:step]。 如果我们不传递 start&…...
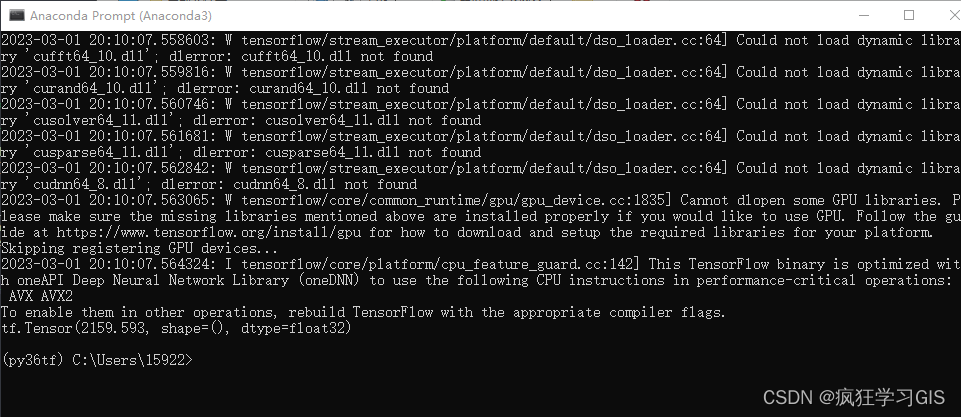
Anaconda配置Python新版本tensorflow库(CPU、GPU通用)的方法
本文介绍在Anaconda环境中,下载并配置Python中机器学习、深度学习常用的新版tensorflow库的方法。 在之前的两篇文章基于Python TensorFlow Estimator的深度学习回归与分类代码——DNNRegressor(https://blog.csdn.net/zhebushibiaoshifu/article/detail…...
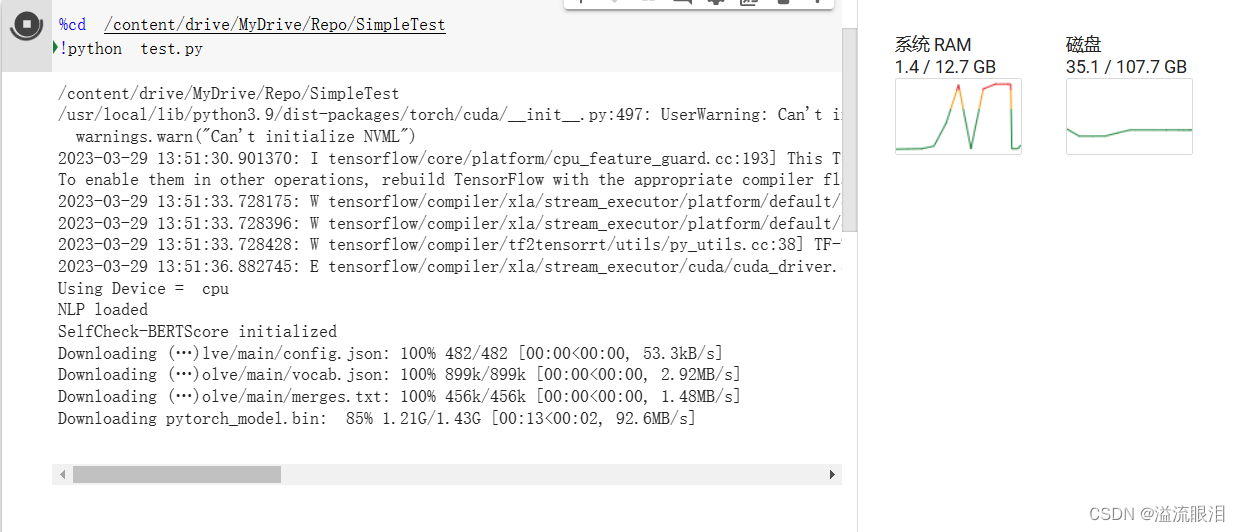
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决报错信息原因查明网传解决措施好消息我的解决措施报错信息 查了下,在网上还是个比较常见的报错 一般为加载某模型时突然报错 原因查明 一般为下载某个 XXX_model.bin 的…...

sessionStorage , localStorage 和cookie的区别
一.sessionStorage(临时存储)sessionStorage是HTML5中新增的Web Storage API之一,用于在浏览器中存储键值对数据,与localStorage类似,但是sessionStorage存储的数据在会话结束时会被清除。可以通过以下方式使用sessionStorage:存储…...

C# 实例详解委托之Func、Action、delegate
委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,这个文章主要就这三种委托的用法通过实例展开讲解。 【Func】:Func是带返回值的委托: 原型函数如下(以下展示的…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
