LeetCode:1184. 公交站间的距离 一次遍历数组,复杂度O(n)
1184. 公交站间的距离
today 1184 公交站间的距离
题目描述
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
输入:distance = [1,2,3,4], start = 0, destination = 1
输出:1
解释:公交站 0 和 1 之间的距离是 1
示例 2:
输入:distance = [1,2,3,4], start = 0, destination = 2
输出:3
解释:公交站 0 和 2 之间的距离是 3
示例 3:
输入:distance = [1,2,3,4], start = 0, destination = 3
输出:4
解释:公交站 0 和 3 之间的距离是 4
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
题目解析
这道题目是一道关于环形公交路线的题目。
首先,我们可以将环形公交路线看作是一个环,然后我们可以从 start 出发,沿着顺时针方向行驶,直到到达 destination,这样得到的距离为sum1。
我们再从 destination 出发,沿着逆时针方向行驶,直到到达 start,这样得到的距离为sum2,最后我们返回 min(sum1, sum2)。
值得注意的是,sum1和sum2的和为整个环路的距离。因此我们可以通过一次遍历,解决问题。
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
代码实现
Python版本:
class Solution(object):def distanceBetweenBusStops(self, distance, start, destination):if start>destination:start,destination=destination,startsum1=sum(distance[start:destination])sum2=sum(distance[:])-sum1return min(sum1,sum2)
C++版本:
class Solution {
public:int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {if (start > destination) {swap(start, destination);}int sum1=0,sum2=0;for(int i=0;i<distance.size();i++){if(i>=start&&i<destination)sum1+=distance[i];elsesum2+=distance[i];}return min(sum1,sum2);}
};
Go版本:
func distanceBetweenBusStops(distance []int, start, destination int) int {if start > destination {start, destination = destination, start}sum1, sum2 := 0, 0for i, j := range distance {if start <= i && i < destination {sum1 += j} else {sum2 += j}}return min(sum1, sum2)
}相关文章:
)
LeetCode:1184. 公交站间的距离 一次遍历数组,复杂度O(n)
1184. 公交站间的距离 today 1184 公交站间的距离 题目描述 环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i 1) % n 的车站之间的距离。 环线上的公交车都…...
)
牛客周赛 Round 60(A,B,C,D,E,F)
比赛链接 官方题解 这场基本都是数学题,官方题解讲的还不错,F能听懂的话其实不难。E是一个球盒模型的组合问题,F是化简递推式,成环时的解决方法很不错。 A 困难数学题 思路: 一个数异或两次结果为 0 0 0ÿ…...
以及记录使用方法)
vueCropper裁剪图片(不模糊)以及记录使用方法
需求:上传限定比例的图片。前端框架是vue3 element plus。 问题:使用vueCropper后比例固定。但是上传后的图片很模糊 vueCropper官网 解决办法 vueCropper中有一个full和high两个参数,记得开启 const options: any reactive({img: , // 原…...
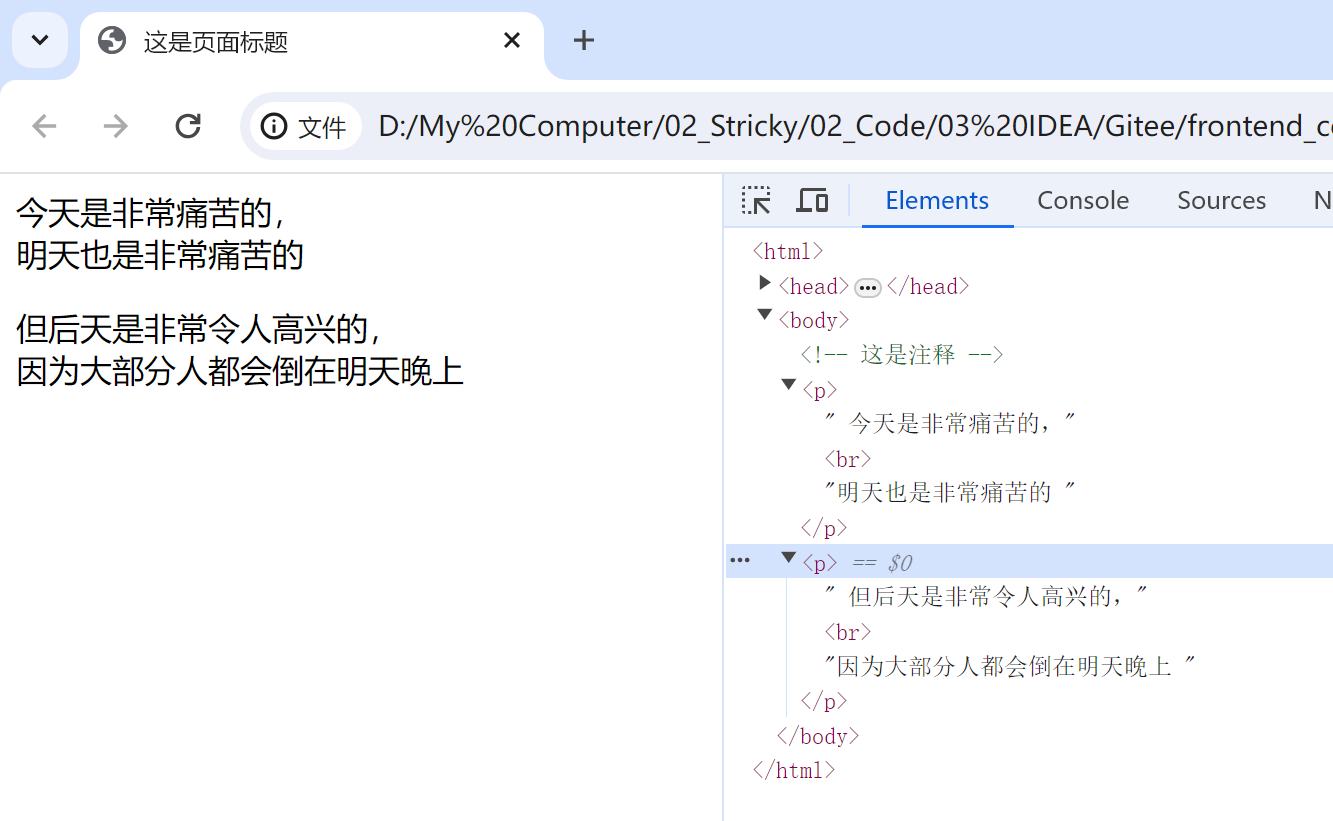
【HTML】HTML页面和常见标签
文章目录 什么是前端HTML 页面编写如何快速生成代码框架常见标签注释标签标题标签段落标签换行标签格式化标签 什么是前端 Web 前端,用来直接给以用户呈现的一个一个的网页。一个软件通常是由 后端前端 完成的 后端:通过 Java/C等语言,完成相…...

鸿蒙 ArkUI组件二
ArkUI组件(续) 文本组件 在HarmonyOS中,Text/Span组件是文本控件中的一个关键部分。Text控件可以用来显示文本内容,而Span只能作为Text组件的子组件显示文本内容。 Text/Span组件的用法非常简单和直观。我们可以通过Text组件来显…...

PHP 实现 redis 分布式锁
分布式锁 如果是强一致性保证,在获取锁或者失败后引入数据库存储扫表、mq 等方式进行补偿 如果可以容忍少量异常就不需要考虑了 像这里的代码,没吃建立一个链接铺货,性能损耗时间延迟也是很大的,也可在一块代码中进行服务&…...

vue3 自定义el-tree树形结构样式
这里样式设置主要用到了 windcss 实现效果 模拟数据 这里也可以用模拟的数据,下面用的是后端请求的真实数据 [{"id": 5,"rule_id": 0,"status": 1,"create_time": "2019-08-11 13:36:09","update_time": "…...
【网络安全】分享4个高危业务逻辑漏洞
未经许可,不得转载。 文章目录 正文逻辑漏洞1逻辑漏洞2逻辑漏洞3逻辑漏洞4其它正文 该目标程序是一家提供浏览器服务的公司,其核心功能是网页抓取和多账户登录操作,类似于浏览器中的隐身模式,但更加强大和高效。通过该平台,用户可以轻松管理并同时运行数百个隐身浏览器实…...

【装机教程】Visual Studio Community 2019离线安装
Visual Studio 2019离线安装 由于现在 官网只支持在线安装最新版的Visual Studio 2022,因此 Visual Studio Community 2019需要离线安装。 下载离线安装镜像,并解压。点击vs_setup.exe运行。 选择安装位置,四处位置需要确定。 选择语言包&…...

NumPy 线性代数
NumPy 线性代数 NumPy 是 Python 中用于科学计算的核心库之一,它提供了一个强大的数学函数库,特别是在处理大型多维数组和矩阵时表现出色。线性代数是 NumPy 的一个重要组成部分,它包含了大量的函数和运算符,用于执行矩阵和向量的…...

家装材料之水泥,最容易被忽视的基础材料!
由于水泥在装修中扮演辅料的角色,很多业主往往会忽视它们的质量。事实上,装修无小事,不能抱有抓大放小的态度。 更何况水泥是装修工程的基础材料,在家居装修中,地面、墙面的找平以及瓷砖、大理石的铺贴&#…...

openstack之keystone介绍
功能 keystone在OpenStack中负责: 管理:用户、租户和权限; 认证:组件相互访问的身份认证; 鉴权:提供 RBAC(Role Based Access Control) 权限体系; 服务注册与发现&#…...

【图像拼接】基于SIFT/SURF特征算法的图像拼接,matlab实现
博主简介:matlab图像代码项目合作(扣扣:3249726188) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 本次案例是基于SIFT/SURF特征算法的图像拼接,用matlab实现。 一、案例背景和算法介…...
《微信小程序实战(2) · 组件封装》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…...

LaTex2024 下载安装运行HelloWorld—全流程笔记
LaTex安装教程🚀 这是读博之后写的第一篇文章,来到新课题组之后,新课题组主要是用Latex,在之前的课题组,还是比较常用world,所以就研究了一下Latex的下载和安装,虽然网上已经有了不少教程&#…...

Golang | Leetcode Golang题解之第404题左叶子之和
题目: 题解: func isLeafNode(node *TreeNode) bool {return node.Left nil && node.Right nil }func sumOfLeftLeaves(root *TreeNode) (ans int) {if root nil {return}q : []*TreeNode{root}for len(q) > 0 {node : q[0]q q[1:]if no…...
基于yolov8+lprnet的中文车牌识别系统python源码+pytorch模型+精美GUI界面
【算法介绍】 基于YOLOv8和LPRNet的中文车牌识别系统是一种高效且准确的解决方案,结合了目标检测与字符识别的先进技术。YOLOv8作为最新的实时目标检测算法,以其高速度和精确度著称,能够迅速在图像或视频中定位车牌位置。LPRNet则是一种专为…...

电信创维光猫DT741超级密码
正常的D740系是创维系列光猫如:SK-D740 之类的超密获取办法-光猫/adsl/cable无线一体机-恩山无线论坛 但是我这个固件是DT741v1.0 我只能说很S -B,这个版本如果是1.02那就可以很轻松的去用通用办法解决,但是呢!还有办法就是用最传…...

PostgreSQL的流复制断点续传
PostgreSQL的流复制断点续传 PostgreSQL的流复制(Streaming Replication)具有断点续传的能力,这意味着当主节点和备用节点之间的连接由于网络故障等原因中断后,备用节点会自动从中断点继续接收WAL(Write-Ahead Loggin…...

【bug】通过lora方式微调sdxl inpainting踩坑
报错内容 ValueError: Attempting to unscale FP16 gradients. 报错位置 if accelerator.sync_gradients:params_to_clip (itertools.chain(unet_lora_parameters, text_lora_parameters_one, text_lora_parameters_two)if args.train_text_encoderelse unet_lora_parameters…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
