【有啥问啥】深入浅出马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)算法

深入浅出马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)算法
0. 引言
Markov Chain Monte Carlo(MCMC)是一类用于从复杂分布中采样的强大算法,特别是在难以直接计算分布的情况下。它广泛应用于统计学、机器学习、物理学等领域,尤其是在贝叶斯推理和概率模型中。本文将深入解析 MCMC 的基本原理、核心算法(如 Metropolis-Hastings 和 Gibbs 采样),并讨论其在实际应用中的优势与局限,同时介绍一些先进的变种如 Hamiltonian Monte Carlo(HMC)。
1. 背景知识
在贝叶斯推断和许多概率模型中,目标是从某个复杂的后验分布 p ( θ ∣ x ) p(\theta | x) p(θ∣x) 中获取样本。然而,在大多数情况下,这种分布很难直接采样,因为其可能涉及到难以求解的归一化常数。
MCMC 提供了一种间接方法,通过构建一个马尔可夫链,使其逐步收敛到目标分布。然后,通过在平衡态(或稳态)下从马尔可夫链中提取样本,我们可以得到接近于目标分布的样本。
2. 马尔可夫链的基础
马尔可夫性质:马尔可夫链是一种具有“无记忆”性质的随机过程,当前状态的下一个状态只依赖于当前状态,而不依赖于历史状态。数学上,设 X 1 , X 2 , … X_1, X_2, \dots X1,X2,… 是马尔可夫链中的状态序列,满足:
P ( X n + 1 ∣ X 1 , X 2 , … , X n ) = P ( X n + 1 ∣ X n ) P(X_{n+1} | X_1, X_2, \dots, X_n) = P(X_{n+1} | X_n) P(Xn+1∣X1,X2,…,Xn)=P(Xn+1∣Xn)
转移矩阵:马尔可夫链通过转移概率矩阵(或转移核)定义,设 P i j P_{ij} Pij 表示从状态 i i i 转移到状态 j j j 的概率,则有:
P i j = P ( X n + 1 = j ∣ X n = i ) P_{ij} = P(X_{n+1} = j | X_n = i) Pij=P(Xn+1=j∣Xn=i)
细致平衡条件:在实际的 MCMC 应用中,重要的是确保马尔可夫链的平稳分布满足“细致平衡条件”(detailed balance)。即:
π ( i ) P i j = π ( j ) P j i \pi(i) P_{ij} = \pi(j) P_{ji} π(i)Pij=π(j)Pji
这一条件保证了链的平稳分布为目标分布。
稳态分布:经过足够多的迭代,马尔可夫链会收敛到一个稳定的分布 π \pi π,该分布满足:
π = π P \pi = \pi P π=πP
在 MCMC 中,我们构建的马尔可夫链会收敛到我们感兴趣的目标分布 p ( θ ∣ x ) p(\theta | x) p(θ∣x)。
举个栗子:
想象一下,你养了一只猫。这只猫在家里随机地游荡,它可能在卧室睡觉、在客厅玩耍、在厨房找吃的,或者在卫生间喝水。这只猫的行动路径就有点像一个马尔可夫链。
- 状态空间: 猫可能存在的各个位置就是它的“状态空间”。在这个例子中,状态空间包括:卧室、客厅、餐厅、厨房和卫生间。
- 转移概率: 猫从一个房间转移到另一个房间的概率就是“转移概率”。比如,猫在卧室里,它可能更喜欢去客厅玩耍,所以从卧室到客厅的转移概率就比较大;而它不太可能直接从卧室跳到天花板上,所以这个转移概率就很小。
- 马尔可夫性质: 猫决定去下一个房间的时候,只考虑它当前所在的房间,而不关心它之前都去过哪些房间。比如,如果猫现在在客厅,它决定去下一个房间的时候,只考虑从客厅能去哪些房间,以及去每个房间的概率,而不会考虑它之前是不是刚从卧室过来。
3. Monte Carlo 方法
Monte Carlo 方法通过随机采样来估计某些不可解析的期望值。设我们需要估计某个分布 p ( x ) p(x) p(x) 下某个函数 f ( x ) f(x) f(x) 的期望:
E p ( x ) [ f ( x ) ] = ∫ f ( x ) p ( x ) d x \mathbb{E}_{p(x)}[f(x)] = \int f(x) p(x) dx Ep(x)[f(x)]=∫f(x)p(x)dx
通过从分布 p ( x ) p(x) p(x) 中采样 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,我们可以用样本均值来近似这个期望:
E p ( x ) [ f ( x ) ] ≈ 1 n ∑ i = 1 n f ( x i ) \mathbb{E}_{p(x)}[f(x)] \approx \frac{1}{n} \sum_{i=1}^n f(x_i) Ep(x)[f(x)]≈n1i=1∑nf(xi)
但正如前述,对于复杂分布,直接采样 p ( x ) p(x) p(x) 往往不可行。这时 MCMC 技术登场,通过马尔可夫链来间接实现从 p ( x ) p(x) p(x) 中采样。
举个栗子:
想象你有一个不规则的图形,比如一个蝙蝠侠形状的图形,你想知道它的面积。这时可以用蒙特卡洛方法,首先,在蝙蝠侠图形外面画一个大的长方形,然后向这个长方形里随机撒豆子,最后通过计算落在蝙蝠侠图形中的豆子比例来估算图形的面积。
4. MCMC 核心算法
4.1 Metropolis-Hastings 算法
Metropolis-Hastings(MH)算法是 MCMC 中常用的采样方法。它通过构造一个易于采样的提议分布 q ( θ ′ ∣ θ ) q(\theta' | \theta) q(θ′∣θ),并通过接受或拒绝的方式生成目标分布的样本。
步骤:
- 初始化 θ 0 \theta_0 θ0
- 对每一轮迭代:
- 根据提议分布 q ( θ ′ ∣ θ t ) q(\theta' | \theta_t) q(θ′∣θt) 生成候选样本 θ ′ \theta' θ′
- 计算接受概率:
α = min ( 1 , p ( θ ′ ∣ x ) q ( θ t ∣ θ ′ ) p ( θ t ∣ x ) q ( θ ′ ∣ θ t ) ) \alpha = \min \left(1, \frac{p(\theta' | x) q(\theta_t | \theta')}{p(\theta_t | x) q(\theta' | \theta_t)}\right) α=min(1,p(θt∣x)q(θ′∣θt)p(θ′∣x)q(θt∣θ′)) - 以概率 α \alpha α 接受 θ ′ \theta' θ′,否则保持当前状态 θ t \theta_t θt
Metropolis-Hastings 的灵活性在于可以使用不同的提议分布来优化采样效率。对于实际问题,选择适当的提议分布 q ( θ ′ ∣ θ ) q(\theta' | \theta) q(θ′∣θ) 是关键,过于分散或集中的分布都可能影响采样效率。
举个栗子(以抽球为例):
- 步骤1:初始化
首先,你闭上眼睛,随机从箱子里摸出一个球,记住这个球的颜色,然后把它放回去。这个球的颜色就是你的起始点,也就是马尔可夫链的初始状态。
- 步骤2:提议生成
接着,你再次闭上眼睛,但这次你稍微改变了一下摸球的方式。你并不是完全随机地摸,而是基于你上次摸到的球的颜色来“提议”一个新的颜色。比如,如果你上次摸到的是红色球,那么你这次可能会倾向于摸一个和红色相近的颜色,比如橙色或紫色(当然,这只是一个比喻,实际中提议分布的选择会更复杂)。这个“提议”的颜色就是你的候选新状态。
- 步骤3:接受-拒绝策略
现在,你需要决定是否接受这个新的颜色作为你下一次摸球的结果。你计算了一个接受概率,这个概率取决于新颜色和旧颜色在箱子中真实出现概率的相对大小,以及你提议分布的一些特性。如果接受概率很高,你就接受这个新颜色;如果很低,你就拒绝它,并保留原来的颜色。
- 步骤4:重复迭代
你不断重复上述步骤,每次都根据当前的颜色来“提议”一个新的颜色,并根据接受概率来决定是否接受它。随着时间的推移,你会发现你摸到的球的颜色分布越来越接近箱子中真实的颜色分布。
4.2 Gibbs 采样
Gibbs 采样是一种特殊的 MCMC 方法,适用于多维随机变量的情况。与 MH 不同,Gibbs 采样通过逐步更新每一个维度的值来生成样本,每次更新都从条件分布中进行采样。
步骤:
- 初始化 θ 0 = ( θ 1 ( 0 ) , θ 2 ( 0 ) , … , θ d ( 0 ) ) \theta_0 = (\theta_1^{(0)}, \theta_2^{(0)}, \dots, \theta_d^{(0)}) θ0=(θ1(0),θ2(0),…,θd(0))
- 对每一轮迭代:
- 对每个维度 i i i:
θ i ( t + 1 ) ∼ p ( θ i ∣ θ 1 ( t + 1 ) , … , θ i − 1 ( t + 1 ) , θ i + 1 ( t ) , … , θ d ( t ) ) \theta_i^{(t+1)} \sim p(\theta_i | \theta_1^{(t+1)}, \dots, \theta_{i-1}^{(t+1)}, \theta_{i+1}^{(t)}, \dots, \theta_d^{(t)}) θi(t+1)∼p(θi∣θ1(t+1),…,θi−1(t+1),θi+1(t),…,θd(t))
- 对每个维度 i i i:
- 重复迭代,直到样本收敛。
Gibbs 采样在模型中条件分布易于采样的情况下表现出色,常用于贝叶斯网络或隐马尔可夫模型等。
4.3 Hamiltonian Monte Carlo(HMC)
Hamiltonian Monte Carlo 是一种高级 MCMC 方法,通过引入物理学中的哈密顿动力学,将样本点视为在势能场中运动的粒子。HMC 可以高效探索高维参数空间,避免传统 MCMC 中的低效率。
核心思想:
- 在传统的 Metropolis-Hastings 算法中,采样仅依赖于当前的状态,而 HMC 则利用目标函数的梯度信息来辅助样本生成。
- HMC 不仅能够加快高维参数的探索,还可以有效避免“随机漫步”行为,使得采样更高效。
HMC 被广泛应用于深度贝叶斯学习中,特别是在大规模复杂模型中表现优异。
5. MCMC 的应用
举个栗子:
现在,我们把蒙特卡洛方法和马尔可夫链结合起来,就得到了MCMC方法。假设我们想知道一个复杂分布(比如一个蝙蝠侠形状的区域里豆子的分布)的某些性质(比如平均高度),但是直接计算太难了。我们可以用MCMC方法来做这件事。
-
首先,我们构造一个马尔可夫链,使得这个链的平稳分布(就是链运行很长时间后每个状态出现的概率分布)恰好是我们想要研究的那个复杂分布。这通常需要我们精心设计马尔可夫链的转移概率。
-
然后,我们从马尔可夫链的某个初始状态开始,按照转移概率随机地移动,生成一系列的状态(就像猫一样)。在刚开始的时候,这些状态可能并不符合我们想要的分布,但是随着链的运行,这些状态会越来越接近我们想要的分布。
-
最后,当我们认为链已经运行了足够长的时间,达到了平稳分布时,我们就可以用这些状态来估算我们想要知道的性质了。比如,我们可以用这些状态来估算蝙蝠侠形状区域里豆子的平均高度。
MCMC 被广泛应用于各种复杂模型中,特别是在贝叶斯推理中。以下是几个典型的应用领域:
-
贝叶斯推断:在贝叶斯推理中,通常需要从后验分布 p ( θ ∣ x ) p(\theta | x) p(θ∣x) 中采样,而该分布可能非常复杂,难以直接采样。MCMC 方法使得这种采样成为可能。
-
隐变量模型:如混合高斯模型(GMM)、隐马尔可夫模型(HMM)等模型中,往往包含不可观测的隐变量。MCMC 可以帮助我们通过采样这些隐变量来进行模型的推断。
-
物理模拟:在物理学领域,如分子动力学模拟、气候模型、材料科学中,MCMC 是估计复杂概率分布的重要工具。
-
深度学习中的贝叶斯模型:结合深度学习与贝叶斯推断,MCMC 在神经网络参数估计、模型选择等方面有了广泛的应用,尤其是在不确定性估计上有明显优势。
6. MCMC 的优势与挑战
优势:
- 适用于复杂的后验分布,尤其是在高维空间下。
- Metropolis-Hastings 和 Gibbs 采样等算法都相对容易实现且适应性强。
- Hamiltonian Monte Carlo 等高级方法可以在高维空间中提高采样效率。
挑战:
- 收敛性问题:确保链的收敛是一个核心挑战,通常需要设置足够长的 burn-in 阶段,以消除初始状态的影响。如何判断链已经收敛仍是一个开放问题。
- 计算成本高:在高维复杂模型中,MCMC 采样的计算成本可能非常高,尤其是每次采样都需要计算大量的概率值。即使使用 HMC,梯度计算的开销也不容忽视。
- 样本自相关性:MCMC 方法生成的样本往往具有自相关性,需要通过后处理(如细化链或降采样)来减小这种影响。
7. 总结
Markov Chain Monte Carlo(MCMC)为我们提供了一种强大的工具,用于从复杂分布中进行采样,特别是在贝叶斯推断和概率模型中具有广泛的应用。尽管 MCMC 存在一定的收敛性和效率挑战,但随着算法的优化和硬件性能的提升,其在机器学习、统计学等领域的应用前景依旧广阔。
诸如 Hamiltonian Monte Carlo(HMC)等高级变种,以及结合深度学习的方法(如变分推断与 MCMC 的混合使用),可能会进一步提升 MCMC 在大规模数据中的表现,使其在更广泛的领域中发挥作用。
相关文章:

【有啥问啥】深入浅出马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)算法
深入浅出马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)算法 0. 引言 Markov Chain Monte Carlo(MCMC)是一类用于从复杂分布中采样的强大算法,特别是在难以直接计算分布的情况下。它广泛应用于统计学、机器学习…...

java企业办公自动化OA
技术架构: sshjbpm 功能描述: 用户管理,岗位管理,部门管理,权限管理,网上交流,贴吧,审批流转。权限管理是树状结构人性化操作,也可以用作论坛。 效果图:...

【leetcode】树形结构习题
二叉树的前序遍历 返回结果:[‘1’, ‘2’, ‘4’, ‘5’, ‘3’, ‘6’, ‘7’] 144.二叉树的前序遍历 - 迭代算法 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,…...

在ros2中安装gazebo遇到报错
安装命令: sudo apt-get install ros-${ROS_DISTRO}-ros-gz 报错如下: E: Unable to locate package ros-galactic-ros-gz 解决方法: 用如下安装命令: sudo apt install ros-galactic-ros-ign 问题解决!...
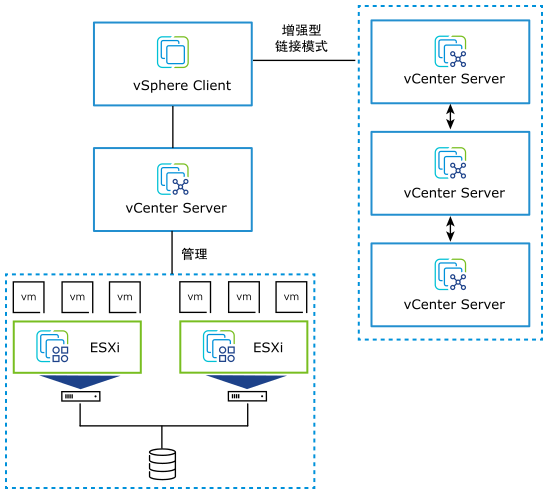
VMware vSphere 8.0 Update 3b 发布下载,新增功能概览
VMware vSphere 8.0 Update 3b 发布下载,新增功能概览 vSphere 8.0U3 | ESXi 8.0U3 & vCenter Server 8.0U3 请访问原文链接:https://sysin.org/blog/vmware-vsphere-8-u3/,查看最新版。原创作品,转载请保留出处。 作者主页…...

在设计开发中,如何提高网站的用户体验?
在网站设计开发中,提高用户体验是至关重要的。良好的用户体验不仅能提升用户的满意度和忠诚度,还能增加转化率和用户留存率。以下是一些有效的方法和策略: 优化页面加载速度 减少HTTP请求:合并CSS和JavaScript文件以减少HTTP请求…...

油耳拿什么清理比较好?好用的无线可视挖耳勺推荐
油耳的朋友通常都是用棉签来掏耳。这种方式是很不安全的。因为使用棉签戳破耳道和棉絮掉落在耳道中而引起感染的新闻不在少数。在使用过程中更加建议大家可视挖耳勺来清理会更好。不仅清晰度得干净而且安全会更高。但最近这几年我发现可视挖耳勺市面上不合格产品很多࿰…...

永久配置清华源,告别下载龟速
为了每次使用 pip 时自动使用清华源,可以通过以下步骤进行配置: 方法一:通过命令行配置 你可以在命令行中运行以下命令来自动设置清华源: pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple此命令会将…...

什么是数据库回表,又该如何避免
目录 一. 回表的概念二. 回表的影响三. 解决方案1. 使用覆盖索引2. 合理选择索引列3. 避免选择不必要的列4. 分析和优化查询5. 定期更新统计信息6. 避免使用SELECT DISTINCT或GROUP BY7. 使用适当的数据库设计 数据库中的“回表”是指在查询操作中,当数据库需要访问…...

UE5中使用UTexture2D进行纹理绘制
在UE中有时需要在CPU阶段操作像素,生成纹理贴图等,此时可以通过UTexture2D来进行处理,例子如下: 1.CPP部分 首先创建一个蓝图函数库,将UTexture2D的绘制逻辑封装成单个函数: .h: #include &…...

Matlab simulink建模与仿真 第十六章(用户定义函数库)
参考视频:simulink1.1simulink简介_哔哩哔哩_bilibili 一、用户定义函数库中的模块概览 注:MATLAB版本不同,可能有些模块也会有差异,但大体上区别是不大的。 二、Fcn/Matlab Fcn模块 1、Fcn模块 双击Fcn模块,在对话…...

每天练打字2:今日状况——完成击键5第1遍,赛文速度74.71
今日跟打:604字 总跟打:99883字 记录天数:2435天 (实际没有这么多天,这个是注册账号的天数) 平均每天:41字 练习常用单字中500,击键5,键准100%,两遍。&#x…...
)
给新人的python笔记(一)
元组与列表 元组使用圆括号()而不是[]列表的元素可以修改,但元组的元素不能修改 创建元组 menu1 (meat,fish,chicken) 访问元组 print(menu[1:3]) 修改元组 不支持 元组内置函数 len(tuple):计算元组中元素个数;…...

如何实现异步并发限制
如何实现异步并发限制 文章目录 如何实现异步并发限制方法1注意点 方法2题目要求实现方法注意点 之前一直没有系统的去总结异步并发限制的实现思路,今天就来做个总结吧 方法1 只有一个变量 pool:代表正在执行中的任务中的集合 function sleep(name, t…...

孙怡带你深度学习(2)--PyTorch框架认识
文章目录 PyTorch框架认识1. Tensor张量定义与特性创建方式 2. 下载数据集下载测试展现下载内容 3. 创建DataLoader(数据加载器)4. 选择处理器5. 神经网络模型构建模型 6. 训练数据训练集数据测试集数据 7. 提高模型学习率 总结 PyTorch框架认识 PyTorc…...

如何在Android上实现RTSP服务器
技术背景 在Android上实现RTSP服务器确实是一个不太常见的需求,因为Android平台主要是为客户端应用设计的。在一些内网场景下,我们更希望把安卓终端或开发板,作为一个IPC(网络摄像机)一样,对外提供个拉流的…...

代理导致的git错误
问题: 今天在clone时出现如下错误: fatal: unable to access https://github.com/NirDiamant/RAG_Techniques.git/: Failed to connect to 127.0.0.1 port 10089 after 2065 ms: Couldnt connect to server真是让人感到奇怪!就在前天&#…...

Ready Go
本文首发在这里 温馨提示 XX年,指的是20XX年,后跟以前、以后之类,均包含本数链接较多,只是想言之有物,已拒绝相同外链,仅看关心的即可已尽量只引用自己的东西,16年后仓库(11/13),2…...

Matlab simulink建模与仿真 第十三章(信号通路库)
参考视频:simulink1.1simulink简介_哔哩哔哩_bilibili 一、信号通路库中的模块概览 1、信号通路组 注:部分模块在第二章中有介绍,本章不再赘述。 2、信号存储和访问组 二、总线分配模块 Bus Assignment模块接受总线作为输入,并…...

Java中接口和抽象类的区别(语法层面的区别、设计理念层面的区别)
文章目录 1. 语法层面的区别1.1 成员属性1.2 成员方法1.3 关系 2. 设计理念层面的区别(重点)3. 举例理解抽象类和接口在设计理念层面的区别3.1 例一:门和警报3.2 例二:招聘3.3 例三:装修房子 4. 总结 1. 语法层面的区别…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
