MySQL底层为什么选择用B+树作为索引
首先,我们来想想为什么这么多数据结构,为什么要用树这种数据结构?
众多的数据结构在逻辑层面可分为:线性结构 和 非线性结构。
线性结构有:数组、链表,基于它们衍生出的有哈希表(哈希表也称散列表)、栈、队列等。
非线性结构有:树、图。
还有其他数据结构如:跳表、位图 也都由基础数据结构演化而来,不同的数据结构存在即都是为了解决某些场景问题。
如果要知道索引适合什么数据结构,那我们得先来回答索引需要来解决什么样的问题(痛点)?和发挥着什么样的作用?其次再才是选择什么样的数据结构;后者只是果,前者才是因。
我们都知道MySQL存储的数据是在磁盘里,因为即使设备断电,放在磁盘的数据是不会有影响的,保障了数据不丢失,这意味着MySQL在磁盘上的数据是持久化的。
但数据存储在磁盘得到保障的同时也是有代价的,这代价就是磁盘的处理速度是毫秒级别的,相比内存纳秒级别的速度,简直是小巫见大巫。
这里简单介绍一下跳图的概念:
跳表底层实质就是可以进行二分查找的有序链表。而且在链表基础加上索引层。即能支持插入、删除等动态操作,也支持按区间高效查询。而且不管是查找、插入、删除对应的时间复杂度都是 O(logn)。
要理解跳表,先来看链表,假设链表存储是有序的数据,我们要想查询某一个数据,在最差的情况下要从头全遍历整个链表,时间复杂度是 O(n)。

从上图所示,我们如果要查询一个 26 的节点,跳表就可以先从索引层遍历,当遍历到在索引层的 21 节点,会发现下一个索引层的节点是 36 节点时,很明显要找的 26 的节点就在这区间。此时我们只要再通过索引层指向原始链表的指针往下移到原始链这一层遍历,只要遍历 2 个节点即可找到 26 了。如果用原来的链表需要遍历 10 个节点,现在只要遍历 8 个节点。

如下图中,一图胜千言。当数据量大时,一个包含多个结点的链表,在建立了五级索引后可以突显的看到索引层的优势。同时注意道这样一个规律 “加一层索引,查询所需要遍历的节点个数减少,查询效率也就提高了。” (从用户的角度就是,跳表这家伙其实就是在告诉链表从什么地方开始找比较快)

那为什么不用跳表作为MySQL的底层索引结构呢?
可以从尽量减少从磁盘查询这个角度寻找答案,这里就不做过多描述了~
接下来看树,这么多树,为什么要选择B+树?
直接跳到AVL(平衡二叉树)树来讲讲,AVL树可以保证每一个节点他的左右子树的高度差都不会超过1,这样相较于二叉查找树来讲可以有效防止链化,但是随着数据变多,这棵树整个高度也会变高,同样会提高磁盘的查询效率~
为了解决这样的问题,我们后面又引入了B树(B-树),因为B树这种数据结构他的一个节点就可以存在多个子节点,同时,一个节点里面又可以存储多个元素,这样就有效解决了前面AVL树带来的问题

那我们来看一下上图所示,当一颗3阶的B树查找 90 这个的元素时的流程是怎么样的?
先从根节点出发,也就是 磁盘块1,判断 90 在17 ~ 35之间,通过磁盘块1中的指针 p3 找到磁盘块4。还是按照原来的步骤,在磁盘块4中的65 ~ 87之间相比较,最后磁盘4的指针p3找到磁盘块11。也就找到有匹配90的键值。
可以发现一颗3阶的B树在查找叶子节点时,由于树高度只有 3,所以查找过程最多只需要3次的磁盘I/O操作。
数据量不大时可能不太真切。但当数据量大时,节点也会随着增多;此时如果还是前面的自平衡二叉树的场景下,由于二叉树只能最多2个叶子节点的约束,也只能纵向去的去扩展子节点,树的高度会很高,意味着需要更多的操作磁盘I/O次数。而B树则可以通过横向扩展节点从而降低树的高度,所以效率自然要比二叉树效率更高。(直白说就是变矮胖了)
看到这,相信你也知道如果B树这么适合,也就没有接下来B+树的什么事了。
接着,那为什么不用B树,而用了B+树呢?
你看啊,B树其实已经满足了我们最前面所要满足的条件,减少磁盘I/O操作,同时支持按区间查找。但注意,虽然B树支持按区间查找,但并不高效。例如上面的例子中,B树能高效的通过等值查询 90 这个值,但不方便查询出一个区间内3 ~ 10区间内所有数的结果。因为当B树做范围查询时需要使用中序遍历,那么父节点和子节点也就需要不断的来回切换涉及了多个节点会给磁盘I/O带来很多负担。
好,那最后我们再来看看为什么要用B+树?
B+树这种结构他的每一个节点存放的都是索引,所有值都是存放在叶子结点里面的,而叶子节点之间构成一个从小到大有序的链表互相指向相邻的叶子节点,也就是叶子节点之间形成了有序的双向链表。

所以,相对于B树而言,B+树在删除节点过程中会添加复杂的删除节点的操作,没有冗余节点,但是对于B+树来说,只会在叶子结点上进行操作,非叶子节点不做处理,有冗余节点,但是不会涉及到复杂的树变形;而且对于插入来讲,B+树的插入最多也只需要修改一条路径,也不涉及复杂度算法实现,可以类似于红黑树的旋转去实现平衡。
相关文章:

MySQL底层为什么选择用B+树作为索引
首先,我们来想想为什么这么多数据结构,为什么要用树这种数据结构? 众多的数据结构在逻辑层面可分为:线性结构 和 非线性结构。 线性结构有:数组、链表,基于它们衍生出的有哈希表(哈希表也称散…...

MATLAB系列05:自定义函数
MATLAB系列05:自定义函数 5. 自定义函数5.1 MATLAB函数简介5.2 在MATLAB中传递变量:按值传递机制5.3 选择性参数5.4 用全局内存分享数据5.5 在函数两次调用之间本地数据的存储5.6 函数的函数(function functions)5.7 子函数和私有函数5.8 总结 5. 自定义…...

C++速通LeetCode简单第20题-多数元素
方法一:暴力解法,放multiset中排序,然后依次count统计,不满足条件的值erase清除。 class Solution { public:int majorityElement(vector<int>& nums) {int ans 0;multiset<int> s;for(int i 0;i < nums.s…...

回收站永久删除的文件还能恢复吗?教你恢复技巧
在数字时代,电脑是我们工作、学习和娱乐的重要工具。然而,随着我们对电脑的频繁使用,误删文件的情况也时有发生。当我们在回收站中不小心永久删除了某个重要文件时,内心可能会充满焦虑和疑惑:这些文件还能恢复吗&#…...

Python Web 微服务架构全面解析与实战指南
Python Web 微服务架构全面解析与实战指南 目录 🏗️ 微服务基础概念 微服务架构与单体架构的对比微服务的优点与挑战 🔄 服务间通信 使用REST、gRPC或消息队列实现服务通信API网关的使用(如Kong、Traefik) 🔍 服务…...

SEAFARING靶场漏洞攻略
寻找漏洞 一,我们打开页面 第一个漏洞 xss漏洞 1.在登录页面显示有弹窗 第二个漏洞 sql注入漏洞 1.在输入框的地方输入-1 union select 1,2,3#我们来查看他的回显点 2.查看数据库表名 -1 union select 1,database(),3# 3.查看表名 -1 union select 1,2,group…...
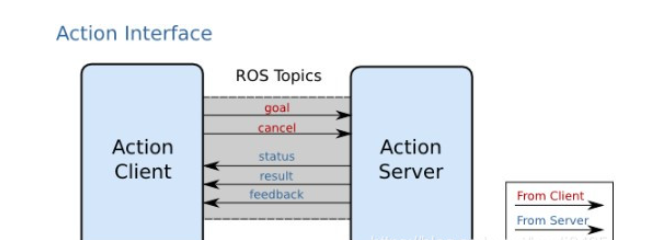
ROS 编程入门的介绍
2.1 创建 ROS 功能包 ROS(Robot Operating System)是一种开源的机器人软件框架,广泛用于机器人开发中。通过使用 ROS,开发者可以轻松创建和管理机器人应用程序。在本节中,我们将介绍如何创建一个 ROS 功能包并实现一些…...

第十一章 抽象类与接口
一、抽象类和抽象方法 抽象类:使用abstract修饰的类 抽象方法:在类中没有方法体的方法,称为抽象方法,抽象方法用abstract修饰 抽象类中可以没有抽象方法,包含抽象方法的类必是抽象类 如果子类没有实现父类中的全部…...

请问企业的八大金刚系统是哪些?有什么共同点和区别?
我的理解的八大金刚包括:MES、ERP、WMS、OMS、CRM、SCM、SRM、PLM。 这些系统的主要功能及运用领域是哪些方面?他们互相之前有什么区别?选择时哪些是企业可能根据自身需求选择的必选项目或可选项目? 由于某些系统的必选性取决于企业的具体业…...

【入门】配置 Java 应用程序的完整指南
前言: Java 是一种广泛使用的编程语言,具备跨平台的特性,使得其应用程序可以在多种环境中高效运行。本文将介绍如何将 Java 应用程序从开发环境部署到生产环境,确保其能够稳定、稳定地运行运行。 确定运行环境 Java程序可以运行…...

flutter widget 设置GestureDetector点击无效
有可能是被上层的widget挡住了,虽然你看得到这个widget,但是操作不到。使用相对布局Stack要特别注意,这种布局会和Android一样,先写的布局放在下层,后写的,如果范围较大的话,会盖在之前的widget…...

基于SpringBoot的在线教育平台的设计与实现
文未可获取一份本项目的java源码和数据库参考。 选题的背景与意义: 随着互联网时代信息技术的不断发展,线下已经产生了很多IT技术的培训机构,但是价格却十分昂贵并且需要人们持续不断的去具体培训地点学习,因此更需要一个课程优…...

Django_Vue3_ElementUI_Release_004_使用nginx部署
1. nginx安装配置 1.1 下载nginx Download nginx 1.2 测试一下 1.3 进入nginx用命令操作 2. 部署 2.1 前端部署 2.1.1 修改nginx监听配置 …conf/nginx.conf http {... # 这里不进行修改server {listen 8010; # 监听 80 端口server_name 192.168.10.24; # 输入服务器 ip…...

Java抽象类的案例
抽象类的特点总结 不能实例化:抽象类不能直接创建实例。它只能被继承。即,你不能用 new 关键字创建抽象类的对象。 可以包含抽象方法:抽象类可以包含一个或多个抽象方法(没有方法体),这些方法必须在子类中…...

运维工程师面试整理-数据库
在运维工程师的面试中,数据库管理和优化是一个非常重要的环节。面试官可能会通过数据库相关的问题来评估你在数据库部署、管理、备份、性能优化以及故障排除方面的能力。以下是关于数据库部分的详细内容,帮助你更好地准备面试。 1. 数据库基础 ● 常见数据库类型 ○ 关系型数…...
comfyui一键抠图工作流:让你告别PS!
前言 本文涉及的工作流和插件,需要的朋友请扫描免费获取哦~ 在当今的数字时代,图像处理已经成为许多行业的日常需求。无论是电商产品展示、广告设计,还是个人照片编辑,去除背景都是一个常见且重要的步骤。 然而,使用…...

【Hot100】LeetCode—4. 寻找两个正序数组的中位数
目录 1- 思路题目识别二分 2- 实现⭐4. 寻找两个正序数组的中位数——题解思路 3- ACM 实现 原题链接:4. 寻找两个正序数组的中位数 1- 思路 题目识别 识别1 :给定两个数组 nums1 和 nums2 ,找出数组的中位数 二分 思路 将寻找中位数 —…...
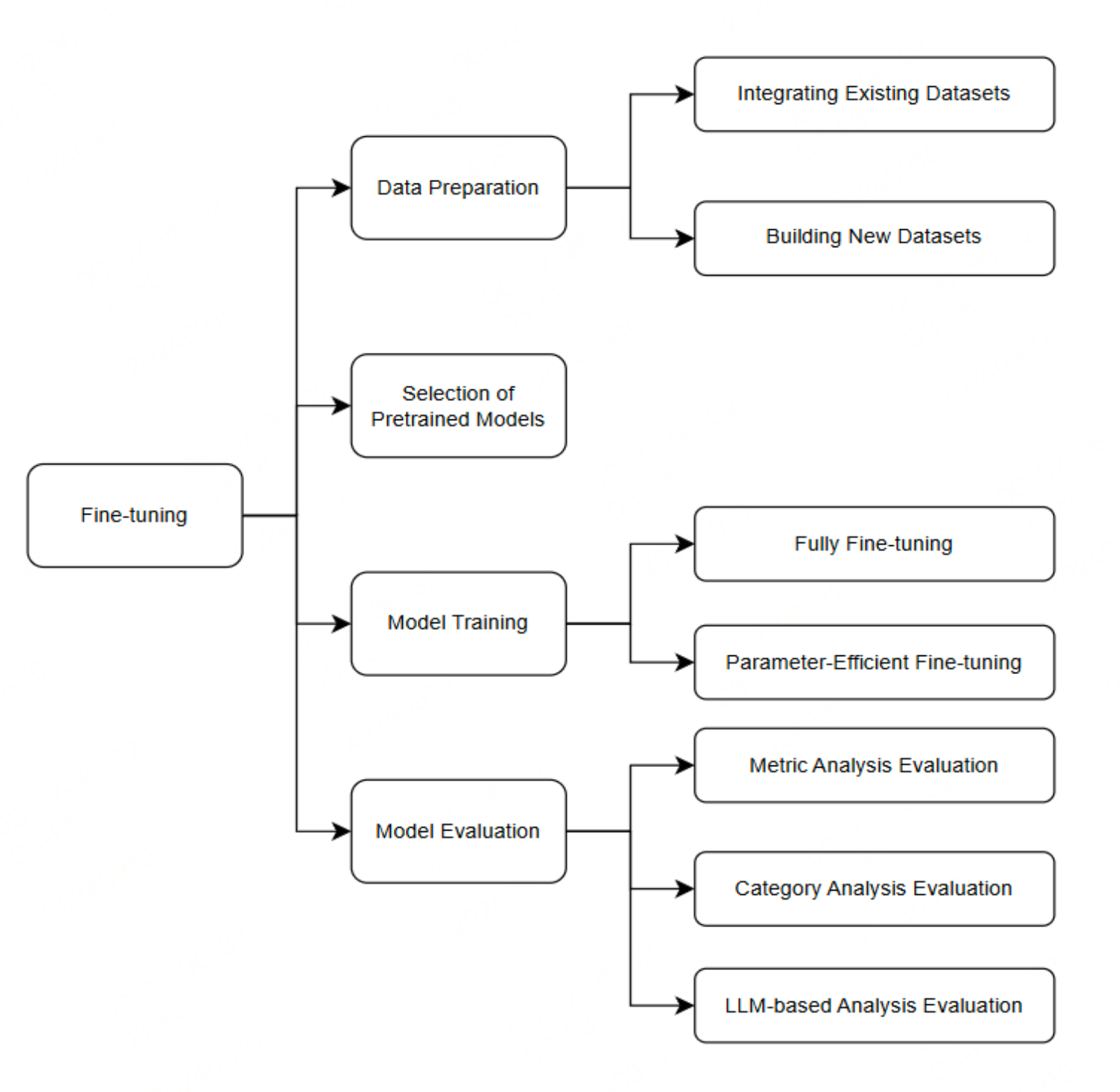
【LLM text2sql】浅看大模型用于text2sql的综述
前言 之前笔者分享了text2sql & LLM & KG的有机结合实现KBQA的问答, 《【LLM & RAG & text2sql】大模型在知识图谱问答上的核心算法详细思路及实践》、 《【开源分享】KBQA核心技术及结合大模型SPARQL查询生成问答实践》。 我们再来看看大模型在te…...
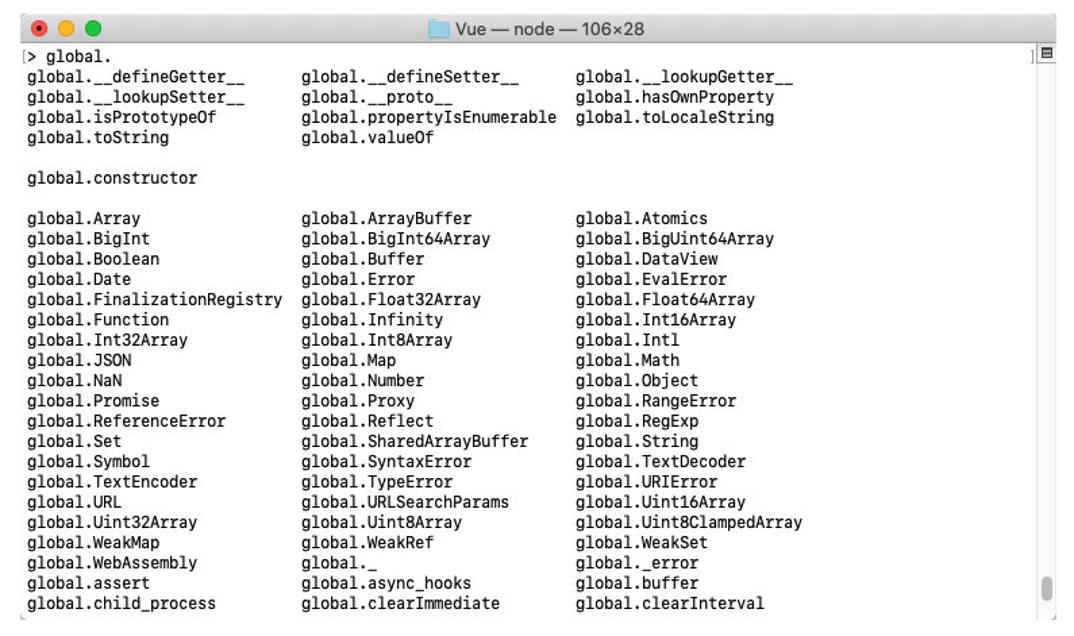
Node js介绍
目录 概要**对Node的认识****Node的概念理解****Node和浏览器区别****Node的架构图** **Node的应用场景****Node的安装****安装Node的LTS版本****Node的版本管理工具nvm(了解)** **Node的输入和输出**Node程序传递参数Node的输出 **Node的全局对象****特殊的全局对象****其他的…...
企业编辑抖音百科词条有什么用?
企业编辑抖音百科词条有什么用? 百科词条创建对企业,品牌以及个人的重要性!#百科词条创建#百科营销#百科词条费用# 企业编辑百科词条主要是有以下这些好处,首先是丰富企业在网络上的信息,提高企业的知名度。 百科词条…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
