leetcode169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3] 输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2] 输出:2
提示:
n == nums.length1 <= n <= 5 * 104-109 <= nums[i] <= 109
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
class Solution {
public:/*** 寻找数组中的多数元素* 多数元素定义为在数组中出现次数大于 n/2 的元素* @param nums 一个整数数组,其中包含多数元素* @return 返回数组中的多数元素*/int majorityElement(vector<int>& nums) {// 计算中间值,用于确定多数元素的条件int mid = nums.size()/2;// 使用哈希表来记录每个元素出现的次数unordered_map<int,int> map;// 用于存储最终找到的多数元素int n;// 遍历数组,统计每个元素的出现次数for(int i = 0; i<nums.size(); i++){map[nums[i]]++;// 如果某个元素出现次数超过中间值,认为找到了多数元素if(map[nums[i]]>mid){n =nums[i];}}// 返回找到的多数元素return n;}
};
相关文章:

leetcode169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出:3 示例…...

从大脑图谱/ROI中提取BOLD信号
动机 在功能连接(Functional Connectivity,FC)构建过程中,由于FC中元素数目是节点数目的平方关系,所以在计算FC之前进行数据降维是一个常见的选择。 一般会将体素级/顶点级BOLD信号(在2mm的图像分辨率下大脑…...

Java-数据结构-优先级队列(堆)-(一) (;´д`)ゞ
文本目录: ❄️一、优先级队列: ➷ 1、概念: ❄️二、优先级队列的模拟实现: ➷ 1、堆的概念: ➷ 2、堆的性质: ➷ 3、堆的创建: ▶ 向下调整: ➷ 4、堆的插入和删除: …...

工厂模式(二):工厂方法模式
一、概念 工厂方法模式(Factory Method),定义一个用于创建对象的接口,让子类决定实例化哪一个类。工厂方法使一个类的实例化延迟到其子类。从而使得系统更加灵活。客户端可以通过调用工厂方法来创建所需的产品,而不必…...

【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解
【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解 题目传送门 题解 神奇构造题qaq 简化一下下题目,就是要求 a b c d gcd ( a , b ) lcm ( c , d ) a b c d \gcd(a, b) \operatorname{lcm}(c,d) abcdgcd(a,b)lcm(c,d) 分类讨论 …...
——动态SQL)
MyBatis系统学习(三)——动态SQL
MyBatis 是一款优秀的持久层框架,它通过 XML 或注解方式将 SQL 语句与 Java 对象映射起来。动态 SQL 是 MyBatis 中非常强大的功能之一,能够根据不同的条件动态生成 SQL 语句。动态 SQL 通过各种标签来灵活生成 SQL,从而避免了在代码中拼接 S…...

get_property --Cmakelist之中
get_property 是 CMake 中用于获取目标、目录、变量或文件等属性的命令。它可以提取某个特定属性的值,以便在构建脚本的其他地方使用。 语法 get_property(<variable> <TYPE> <name> PROPERTY <property-name> [SET | DEFINED | BRIEF_DO…...
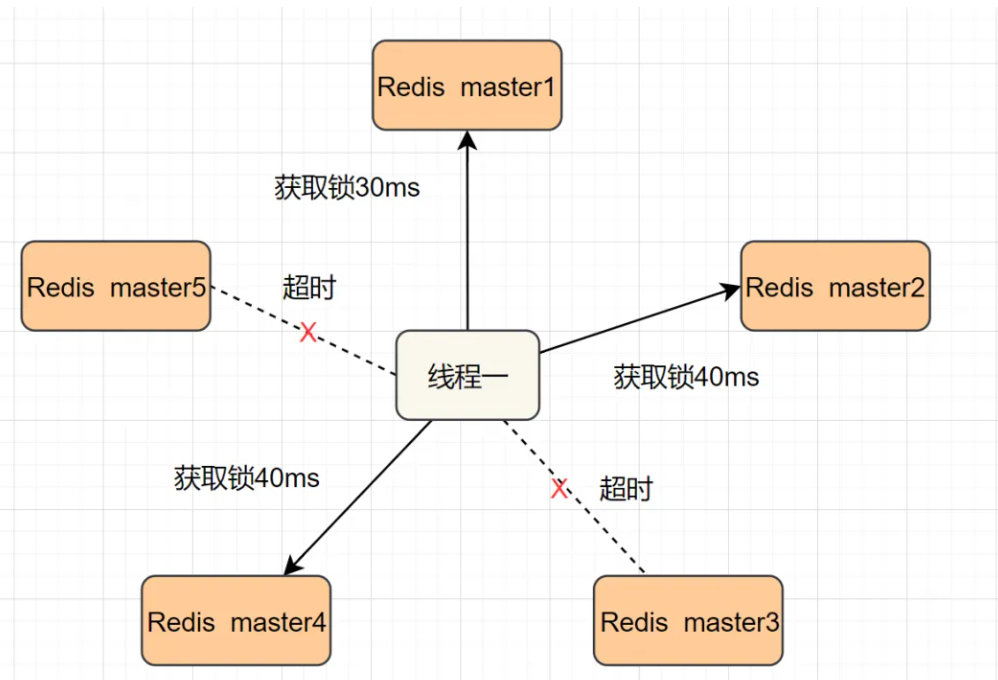
【Redis】Redis 典型应用 - 分布式锁原理与实现
目录 Redis 典型应⽤ - 分布式锁什么是分布式锁分布式锁的基础实现引⼊过期时间引⼊校验 id引⼊ lua引⼊ watch dog (看⻔狗)引⼊ Redlock 算法其他功能 Redis 典型应⽤ - 分布式锁 什么是分布式锁 在⼀个分布式的系统中, 也会涉及到多个节点访问同⼀个公共资源的…...

Pybind11的使用
目录 1. 引言1.1 Pybind11 简介1.2 为什么需要 Pybind11 2. 使用 Pybind11 进行 C 与 Python 交互2.1 基本用法2.2 编译与生成共享库2.2.1 在 Linux 下编译2.2.2 在 macOS 下编译2.2.3 编译选项详解 2.3 在 Python 中使用编译后的模块 3. 高级用法与注意事项3.1 绑定类和复杂数…...

鸿蒙-沉浸式pc端失效
咨询描述: 因PC北向窗口涉及沉浸式时,预计发生接口废弃导致不兼容变更,涉及接口setImmersiveModeEnabledState、setWindowLayoutFullSceen 如果应用支持沉浸式(窗口全屏且隐藏状态栏&标题栏&Dock栏)࿰…...

【资料分析】刷题日记1
第一套 第二个是相比2019年的增长率,错找为同比增长率 延申: 当出口和进口相比2019年的增长率相同时,可以用盐水解决 √ 一个假设分配(第二次是1.4取1)加法对比选项 基期倍数: 求A是B的多少倍&#x…...

nodejs+express+vue教辅课程辅助教学系统 43x2u前后端分离项目
目录 技术栈具体实现截图系统设计思路技术可行性nodejs类核心代码部分展示可行性论证研究方法解决的思路Express框架介绍源码获取/联系我 技术栈 该系统将采用B/S结构模式,开发软件有很多种可以用,本次开发用到的软件是vscode,用到的数据库是…...

96-javahashmap底层原理
HashMap是Java集合框架中的一个重要类,底层是基于哈希表实现的。哈希表是一种数据结构,可以通过哈希函数来提高查找、插入和删除操作的效率。 以下是HashMap底层实现的一些关键点: 哈希算法:HashMap使用哈希算法来计算键的哈希值…...

AI逻辑推理入门
参考数据鲸 (linklearner.com) 1. 跑通baseline 报名 申领大模型API 模型服务灵积-API-KEY管理 (aliyun.com) 跑通代码 在anaconda新建名为“LLM”的环境,并安装好相应包后,在jupyter notebook上运行baseline01.ipynb 2. 赛题解读 一般情况下,拿到一个赛题之后,我们需…...

力扣3014.输入单词需要的最少按键次数I
给你一个字符串 word,由 不同 小写英文字母组成。 电话键盘上的按键与 不同 小写英文字母集合相映射,可以通过按压按键来组成单词。例如,按键 2 对应 ["a","b","c"],我们需要按一次键来输入 "…...

【Git】远程仓库
本博客的环境是 Ubuntu/Linux 文章目录 集中式与分布式的区别远程仓库新建远程仓库克隆远程仓库向远程仓库推送从远程仓库拉取 配置Git忽略指定文件给命令配置别名 标签管理创建标签操作标签 多人协作本地分支与远程分支连接场景一场景二 集中式与分布式的区别 引荐自关于Git这…...

苹果手机铃声怎么设置自己的歌?3个方法自定义手机铃声
苹果手机内部的手机铃声库只有固定的几首铃声,且都是纯音乐,比较单调,并不是所有用户都喜欢这些铃声。那么,苹果手机铃声怎么设置自己的歌呢?小编这里有3个方法,可以教大家如何将手机铃声设置成自己喜欢的歌…...
828华为云征文|华为Flexus云服务器搭建Cloudreve私人网盘
一、华为云 Flexus X 实例:开启高效云服务新篇🌟 在云计算的广阔领域中,资源的灵活配置与卓越性能犹如璀璨星辰般闪耀。华为云 Flexus X 实例恰似一颗最为耀眼的新星,将云服务器技术推向了崭新的高度。 华为云 Flexus X 实例基于…...

【AI学习】AI绘画发展简史
无意中读了一篇发表自2022年的文章,《AI绘画何以突飞猛进? 从历史到技术突破, 一文读懂火爆的AI绘画发展史》,写的比较有意思,科普了好多我原来不知道的历史。 简单提炼一下,做个笔记。 AI绘画重要事件 2012年 Google两位大名…...

使用LangChain创建简单的语言模型应用程序【快速入门指南】
## 引言在这篇文章中,我们将展示如何使用LangChain构建一个简单的语言模型(LLM)应用程序。这个应用程序的功能是将文本从英语翻译成其他语言。尽管应用程序的逻辑相对简单,但它能够帮助我们学习如何使用LangChain进行更多复杂的功…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
