“提效”|教你用ChatGPT玩数据
ChatGPT与数据分析(二)
上文给简单聊了一下为什么ChatGPT不能取代数据分析师,本文我们来深入感受一下如何让GPT帮助数据分析师“提效”。
场景一:SQL取数
背景:多数数据分析师都要用SQL语言从数据库中提取数据,SQL虽然简单,但是写几百行取数代码也是很头疼的一个操作,这个时候不妨交给GPT试一试,示例如下:
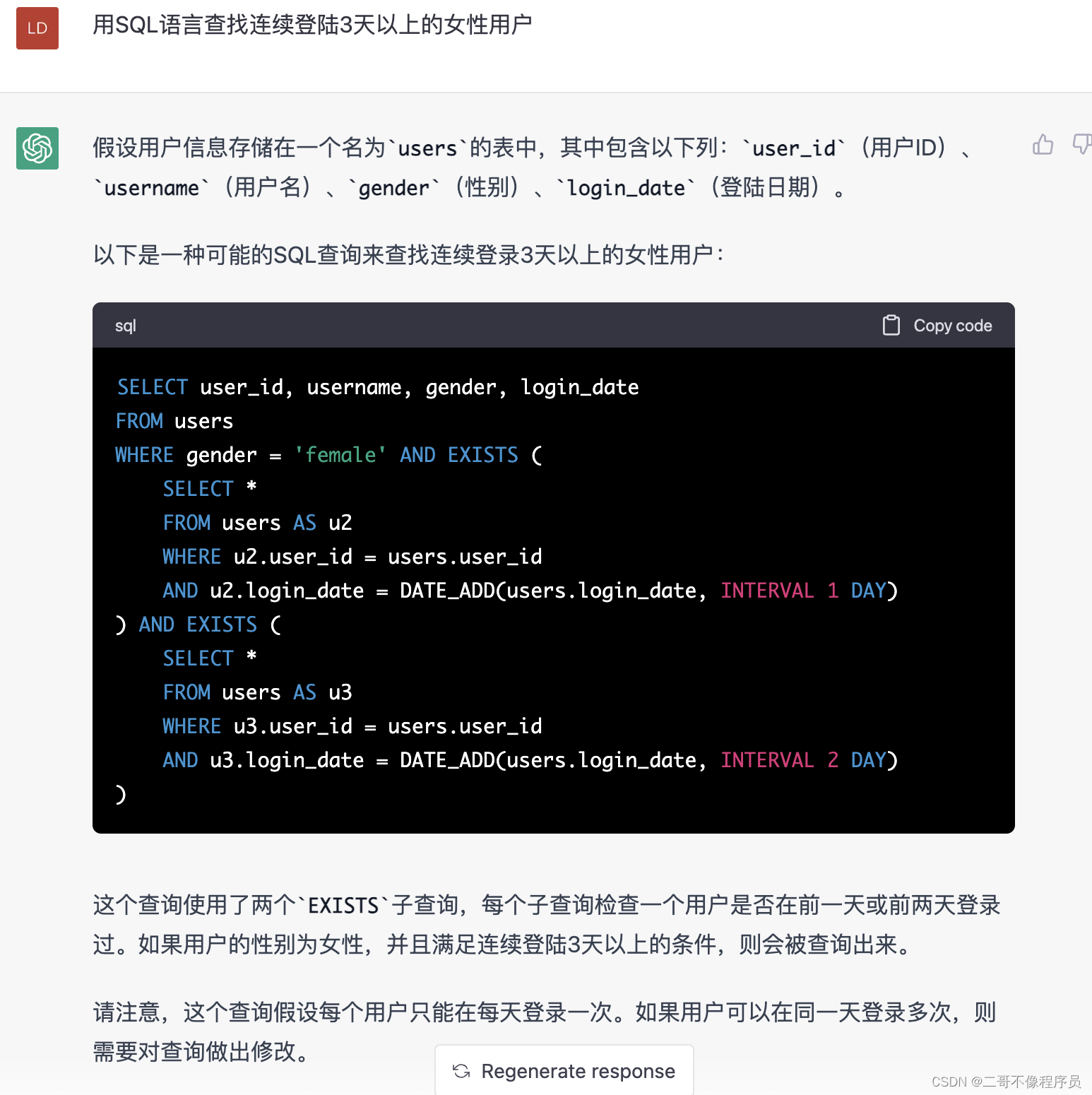
这种简单的写法你可能觉得效率不高,对其嗤之以鼻,别急,把你的想法告诉它,让它来解决。
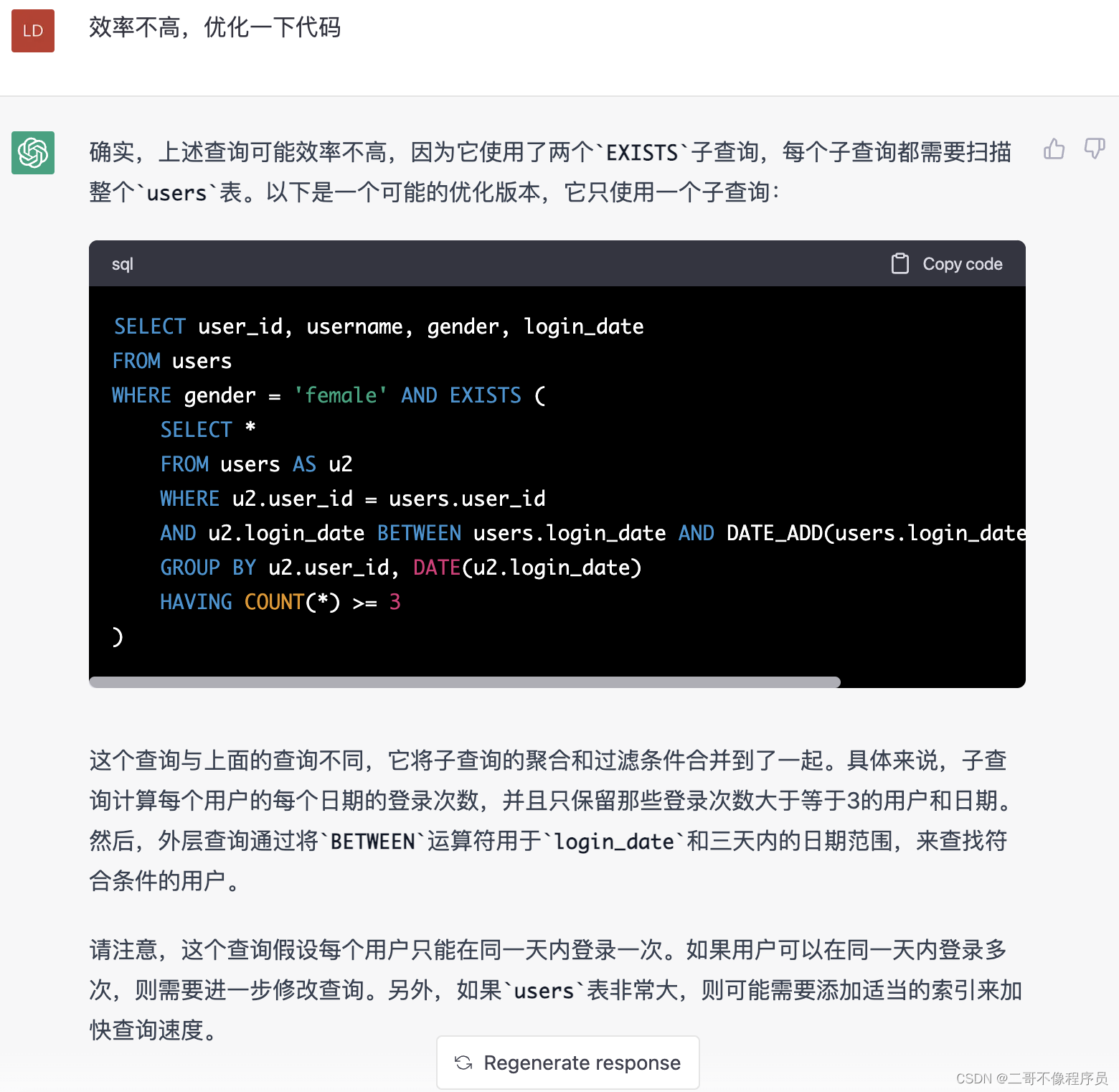
还不行?继续!

总结:简单的说对于SQL任务,告诉GPT你要做的事情,他就会模拟字段给出相应的代码,需要注意的就是AI虽好,但是错误也不少!还是要自己测试一下的。
场景二:Python代码
背景:ChatGPT既然能写SQL,写Python当然也不在话下,示例如下:
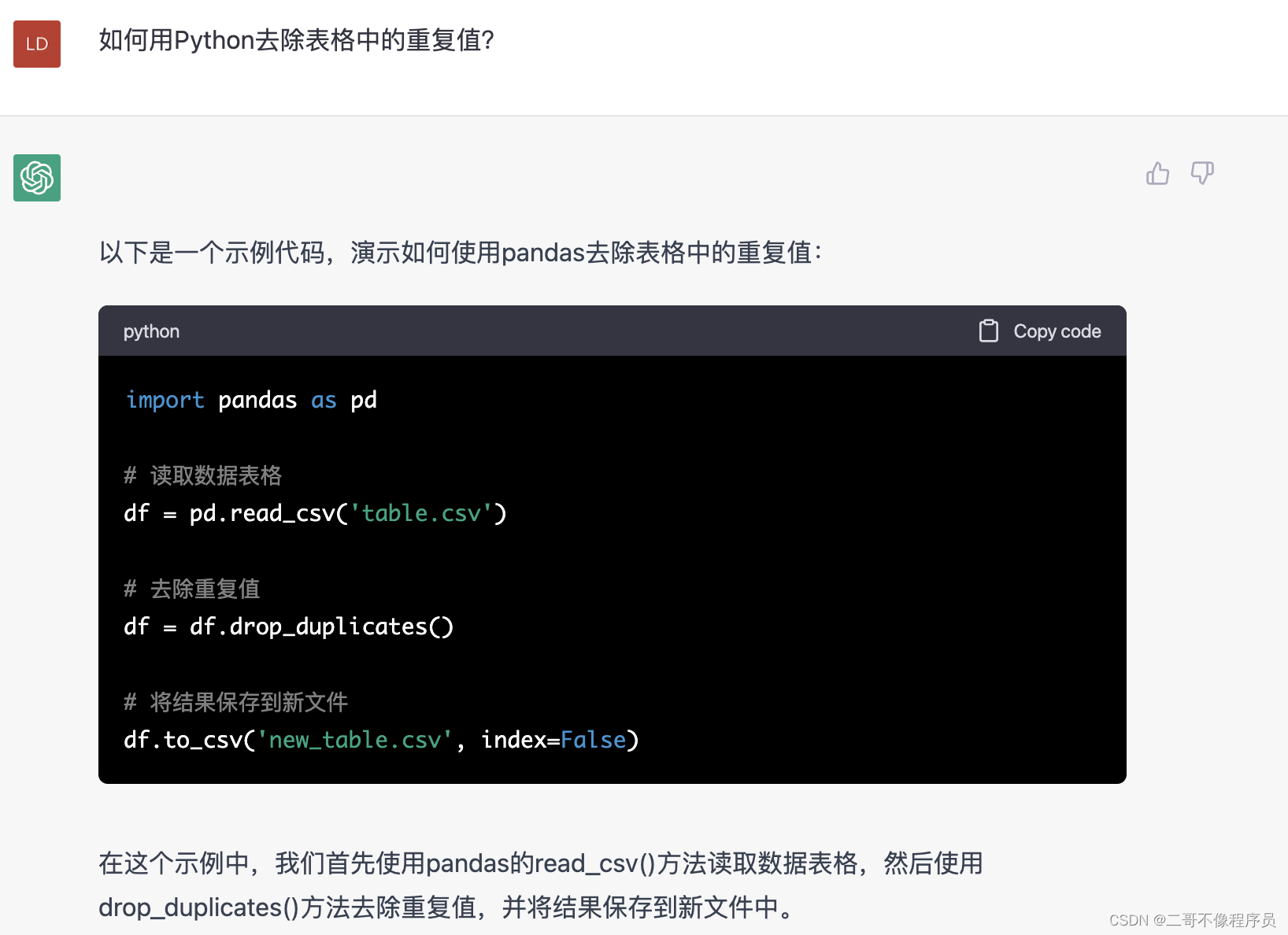
总结:想要用Python处理数据,把你想做的事告诉GPT,他就会教你应该怎么做了。当然除了处理数据,画图的代码也可以让GPT来生成。
注:GPT本质上能够直接生成图片,但是多数情况会由于网络传输原因不显示图片。
场景三:统计学
背景:除了对于数据的操作,很多时候我们也需要进行一些统计学的计算,如显著性检验等,同样的把问题抛给GPT即可。

可以继续从GPT那里得到其他方法(截图不完整,仅供展示)
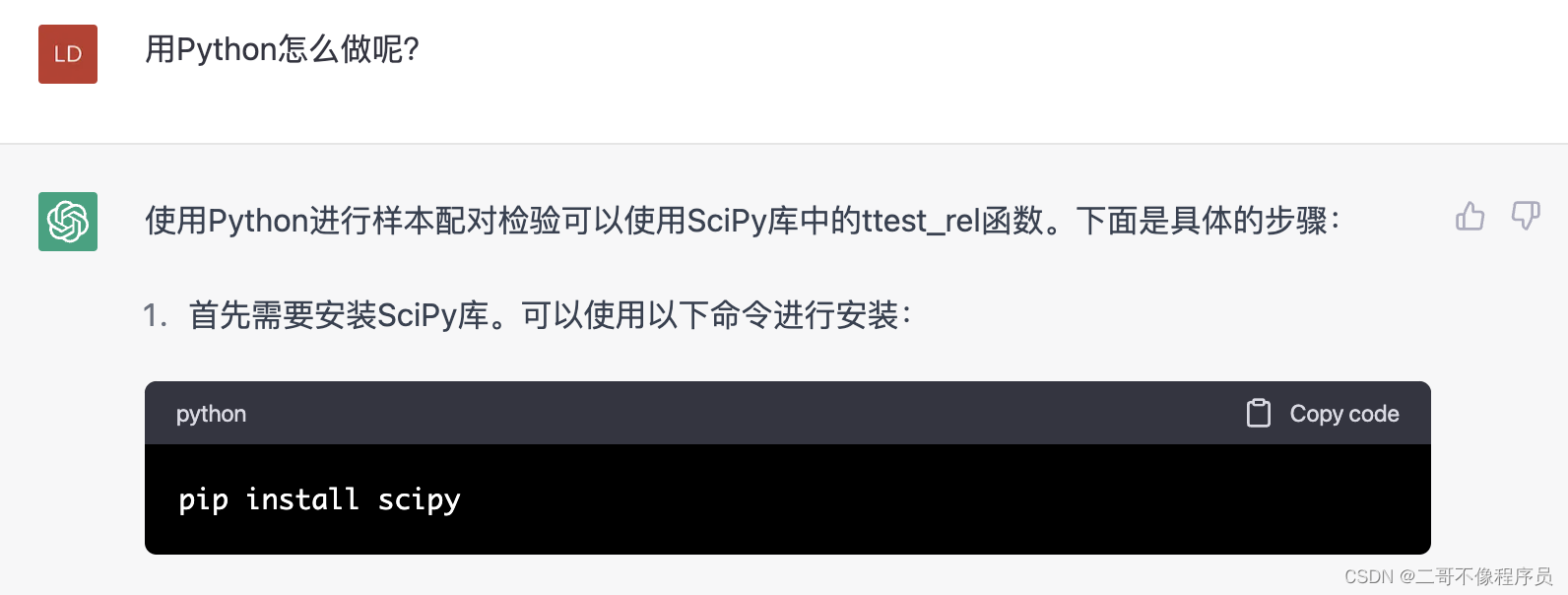
总结:是不是感觉越来越强大了,不仅能帮助我们,还能教我们怎么做。但是!你以为到这就结束了?继续看!
场景四:实验设计
背景:很多时候作为数据分析师,我们需要进行整个分析流程的规划,如A/B实验、复盘分析、运营分析等,这种小问题,交给GPT即可。

总结
随着ChatGPT的不断升级,其强大的功能已经逐渐渗透到各行各业,二哥认为小伙伴们不必对GPT抱有抵触心理,对于我们而言,其本质可以看作是一个更加精准的“百度一下”,平时我们有问题找百度,从各种各样的帖子中拼凑自己需要的东西,GPT的出现大大的节省了我们在无效网页上浪费的时间,也可以说它从准确性上帮助我们起到了“提效”的作用。
相关文章:

“提效”|教你用ChatGPT玩数据
ChatGPT与数据分析(二) 上文给简单聊了一下为什么ChatGPT不能取代数据分析师,本文我们来深入感受一下如何让GPT帮助数据分析师“提效”。 场景一:SQL取数 背景:多数数据分析师都要用SQL语言从数据库中提取数据&#x…...
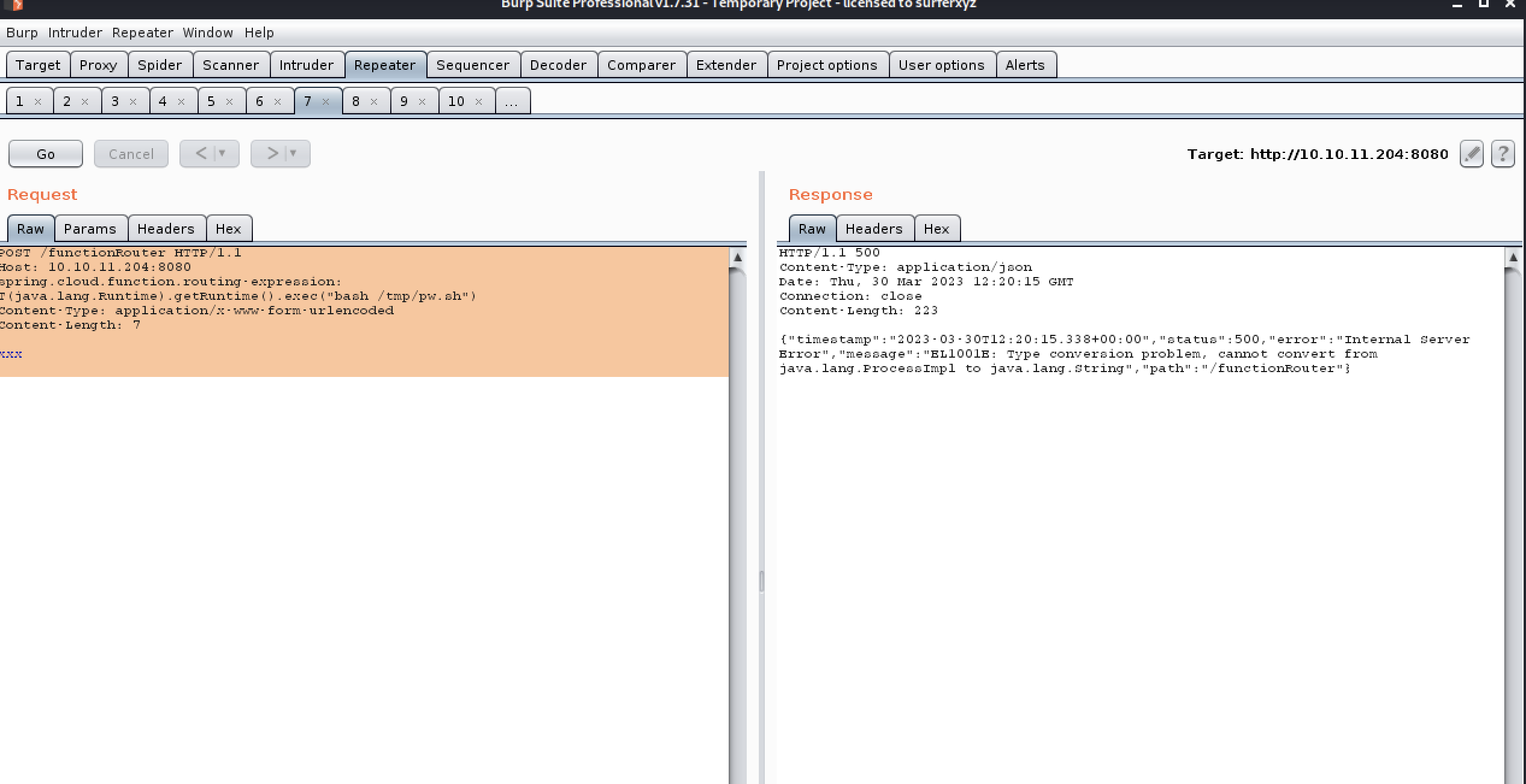
https://app.hackthebox.com/machines/Inject
https://app.hackthebox.com/machines/Inject Ref: 1.https://blog.csdn.net/qq_58869808/article/details/129505388 2.https://blog.csdn.net/m0_73998094/article/details/129474782 info collecting ┌──(kwkl㉿kwkl)-[~/HODL/htb/Inject] └─$ nmap -A …...

Java Web 实战 15 - 计算机网络之网络编程套接字
文章目录一 . 网络编程中的基本概念1.1 网络编程1.2 客户端(client) / 服务器(server)1.3 请求(request) / 响应(response)1.4 客户端和服务器之间的交互数据1.4.1 一问一答1.4.2 多问一答1.4.3 一问多答1.4.4 多问多答二 . socket 套接字2.1 UDP 的 Socket API2.1.1 引子2.1.2…...
基于pdf2docx模块Python实现批量将PDF转Word文档(安装+完整代码教程)
PDF文件是一种常见的文档格式,但是在编辑和修改时不太方便,因为PDF本质上是一种静态的文档格式。因此,有时候我们需要将PDF文件转换成Word格式,以便更好地编辑和修改文档。在本篇文章中,我们将介绍如何使用Python实现P…...
3.21~3.22
识编程语言中的,局部变量,全局变量,以及变量生存周期,整形,浮点型数据的内存表示,od的内存窗口的使用 先看一个代码样例 #include<windows.h> #include<stdio.h>#pragma warning(disable:499…...

Chromium 改造实录:增加 MPEG TS 格式支持
在《选择最新 Chromium,支持 H264 / H265》一文中,记录了我通过升级 Chromium 版本解决了 H264 / H265 视频支持难题。然而难题接踵而至,这次的难题是 MPEG TS 流的支持。MPEG2-TS 传输流广泛应用于数字电视广播系统,所以是一个不…...
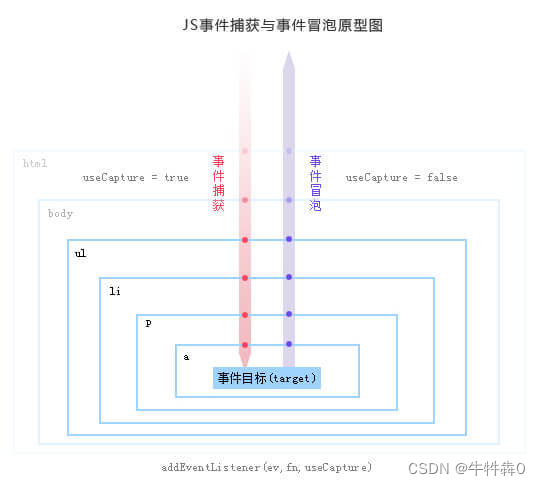
性能优化之-事件代理
js中的事件委托或是事件代理简单理解 事件委托也叫事件代理,“事件代理”即是把原本需要绑定在子元素的响应事件(click、keydown…)委托给父元素,让父元素担当事件监听的职务。事件代理的原理是DOM元素的事件冒泡。 概述&#x…...

MSDS 即化学品安全说明书
MSDS 即化学品安全说明书,亦可译为化学品安全技术说明书或化学品安全数据说明书,是化学品生产商和进口商用来阐明化学品的理化特性(如PH值,闪点,易燃度,反应活性等)以及对使用者的健康ÿ…...

真人手办没法实现网购?我有一个好办法!
记得以前在网上看到过一个冷笑话式的问答,问的是中国最早的手办是什么,有网友回答是秦始皇兵马俑,这个抖机灵式的回答简直妙得让人会心一笑。 你接触过手办吗? 提到手办,大家第一时间想到的,肯定都会是各…...
)
2019湖南省大学生程序设计竞赛题解(D)
D-Modulo Nine 很妙的类似区间dp, 我自己是想不到,本题解题思路来自学长的博客: 长沙橘子猫 题意 有一个长度为 nnn 的序列,你可以给每个位置填 0∼90\sim90∼9 的一个数,有 mmm 个限制,每个限制 [li,ri…...
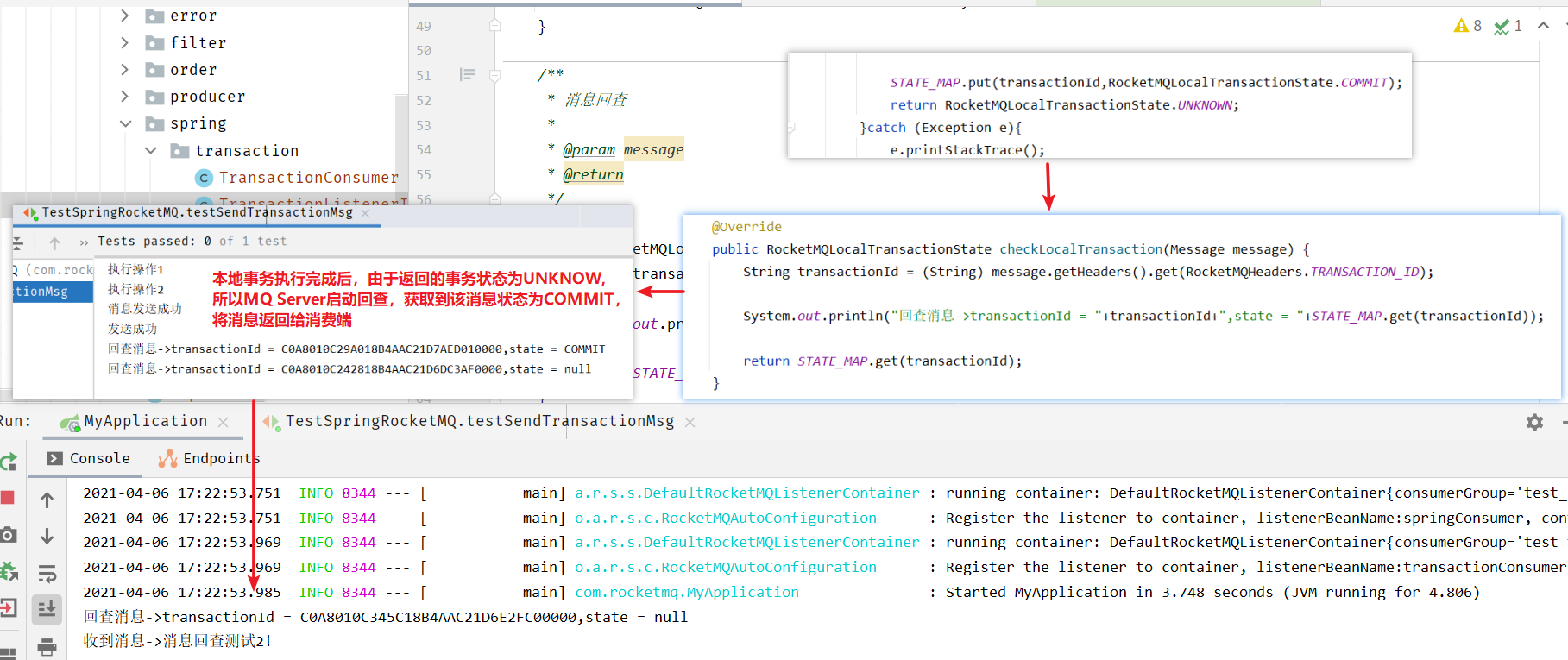
【开发】中间件——RocketMQ
分布式消息系统 RocketMQ概念,用途,特性安装RocketMQ掌握RocketMQ的api使用对producer、consumer进行详解了解RocketMQ的存储特点 简介及相关概念JavaAPISpringBoot整合RocketMQ消息的顺序收发消息系统的事务、存储、重试策略消息系统的集群 RocketMQ R…...
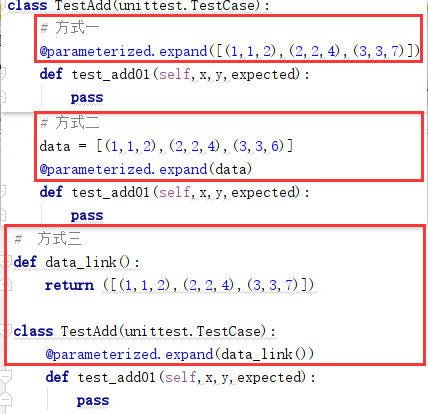
36 UnitTest框架 - 参数化
目录 一、参数化环境准备 1、方式一:在终端(cmd)安装parameterized 2、方式二:在Pycharm中安装parameterized 二、参数化 1、什么事参数化? 2、参数化引入案例 (1)需求 (2&a…...
 事件循环)
Qt源码阅读(四) 事件循环
事件系统 文章为本人理解,如有理解不到位之处,烦请各位指正。 文章目录事件系统什么是事件循环?事件是如何产生的?sendEventpostEvent事件是如何处理的?事件循环是怎么遍历的?事件过滤器event夹带私货时间Q…...

银行数字化转型导师坚鹏:银行数字化领导力提升之道
银行数字化领导力提升之道 ——融合中西智慧,践行知行合一思想,实现知行果合一 课程背景: 很多银行存在以下问题:不知道如何领导数字员工?不清楚银行数字化领导力模型的内涵?不知道如何开展银行数字化…...

Vue2 -- 自定义单选内容的单选框组件
自定义单选内容的单选框组件 之前做的一个项目,在项目中有一个关于人员权限分配的功能,给人员指定各个模块的权限信息,分为 write 可写权限read 可读权限none 没有权限 项目要求画面中只显示 W R 两个按钮控制指定权限信息,都不…...

让PyTorch训练速度更快,你需要掌握这17种方法
掌握这 17 种方法,用最省力的方式,加速你的 Pytorch 深度学习训练。近日,Reddit 上一个帖子热度爆表。主题内容是关于怎样加速 PyTorch 训练。原文作者是来自苏黎世联邦理工学院的计算机科学硕士生 LORENZ KUHN,文章向我们介绍了在…...

LeetCode-309. 最佳买卖股票时机含冷冻期
目录题目思路动态规划题目来源 309. 最佳买卖股票时机含冷冻期 题目思路 每天最多只可能有三种状态中的一种 0表示当前处于买入状态(持有股票) 1表示当前处于卖出状态(不持有股票) 2表示当前处于冷冻状态 设dp[i][j]表示i - 1天状态为j时所拥有的最大现金 dp[i][0] Math.ma…...
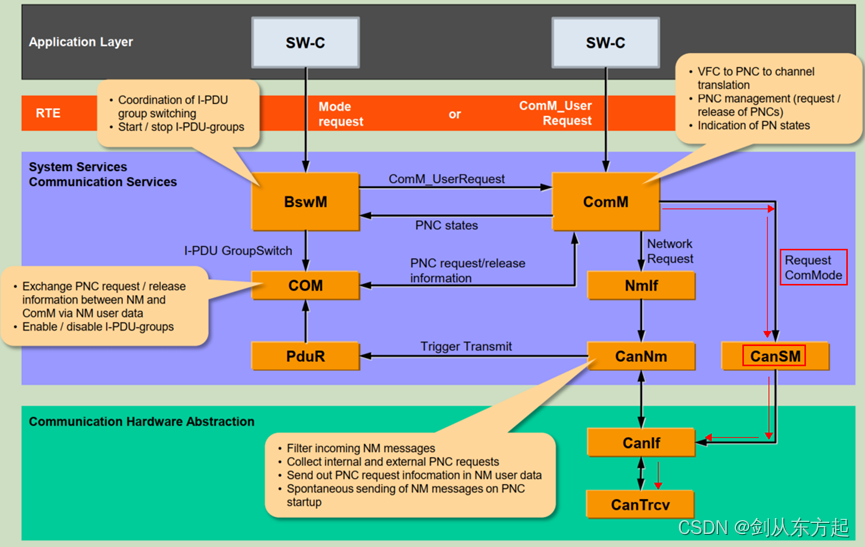
AUTOSAR知识点Com(七):CANSM初认知
目录 1、概述 2、CanSM主要做什么 2.1、CAN控制器状态管理 2.2、CAN收发器状态管理 2.3、Busoff检测 1、概述 CANSM(Controller Area Network State Manager)是AUTOSAR(Automotive Open System Architecture)标准中的一个模块…...

递归:斐波那契数列、递归实现指数型枚举、递归实现排列型枚举
递归:O(2^n) 调用自己 例题及代码模板: 斐波那契数列 输入一个整数 n ,求斐波那契数列的第 n 项。 假定从 0 开始,第 0 项为 0。 数据范围 0≤n≤39 样例 输入整数 n5 返回 5 #include <iostream> #include <cstring&g…...

oracle模糊查询时字段内容包含下划线的解决办法
最近项目中遇到一个关于模糊查询问题。表tabA中的字段name的值有下划线的情况,在模糊查询时发现查询的记录不对。 表的结构 表名:tabA id name sex 1 test_601 1 2 test_602 2 3 test16 1 4 t…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
