2019湖南省大学生程序设计竞赛题解(D)
D-Modulo Nine
很妙的类似区间dp, 我自己是想不到,本题解题思路来自学长的博客: 长沙橘子猫
题意
有一个长度为 nnn 的序列,你可以给每个位置填 0∼90\sim90∼9 的一个数,有 mmm 个限制,每个限制 [li,ri][l_{i}, r_{i}][li,ri] 要求区间内的数相乘必须为 999 的倍数,问一共有多少种合法的填数方案。
思路
破题点:博主在定义自己的方程时意识到,区间是不连续的两个端点组成的,我们枚举前 iii 个数则是一位位顺序来的,这样转移方程就不会很顺利。
于是我们可以尝试往将区间也能随着我们顺序遍历来解决的方向虑,于是就引申出解法中,以右端点编号将所有右端点相同的区间的左端点存入同一个桶的做法。 (实际上我们只需要存最大左端点即可)
而我们每遍历一位数,枚举当前可能填入的数之后就可以着手考虑如何让右端点为 iii 的所有区间合法考虑,因为我们找到只要区间内包含两个及以上的 333 就能保证合法(0/90/90/9 本身就代表两个 333),于是就能引申出dp方程的状态 j,kj,kj,k 分别代表离 iii 最近的两个 333 的位置,dpjkdp_{jk}dpjk,就能轻易根据当前 iii 桶里存储的区间来判断 dpjkdp_{jk}dpjk 的方案合不合法。
代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 60, mod = 1e9 + 7;
int n, m;
ll f[N][N]; //前i个数 当前已经填过的数的最后一个3在j, 倒数第二个在i
vector<int>g[N];void add(ll &x, ll y){x = (x + y + mod) % mod;
}void solve(){for(int i = 0; i <= n; i ++){g[i].clear();for(int j = 0; j <= n; j ++) f[i][j] = 0;}for(int i = 1; i <= m; i ++){int l, r;cin >> l >> r;g[r].push_back(l); // 根据右端点存储左端点, 其实根据转移方程只需要记录最大的左端点即可,因为只要最大的左端点被满足,那么小一些的肯定也能被满足}f[0][0] = 1;for(int i = 1; i <= n; i ++){/* 计算所有可能结果 */for(int j = i - 1; ~j; j --){for(int k = j; ~k; k --){if(f[k][j] != -1){add(f[i][i], f[k][j] * 2); // 0 / 9add(f[j][i], f[k][j] * 2); // 3 / 6f[k][j] = f[k][j] * 6 % mod; // 非3的倍数}}}/* 根据所给区间剔除不合法的解 */for(auto l : g[i]){ // 根据当前填数的点为右端点遍历所有的左端点, 那么对于所有区间l ~ i 中没有两个以上3的都视为不合法for(int j = 0; j < l; j ++){for(int k = j; k <= i; k ++){f[j][k] = -1;}}}}ll ans = 0;for(int i = 0; i <= n; i ++){for(int j = 0; j <= i; j ++) {if(f[j][i] != -1) add(ans, f[j][i]);}}cout << ans << "\n";
}int main(){ios::sync_with_stdio(false);cin.tie(nullptr); cout.tie(nullptr);while(cin >> n >> m){solve();}return 0;
}
相关文章:
)
2019湖南省大学生程序设计竞赛题解(D)
D-Modulo Nine 很妙的类似区间dp, 我自己是想不到,本题解题思路来自学长的博客: 长沙橘子猫 题意 有一个长度为 nnn 的序列,你可以给每个位置填 0∼90\sim90∼9 的一个数,有 mmm 个限制,每个限制 [li,ri…...
【开发】中间件——RocketMQ
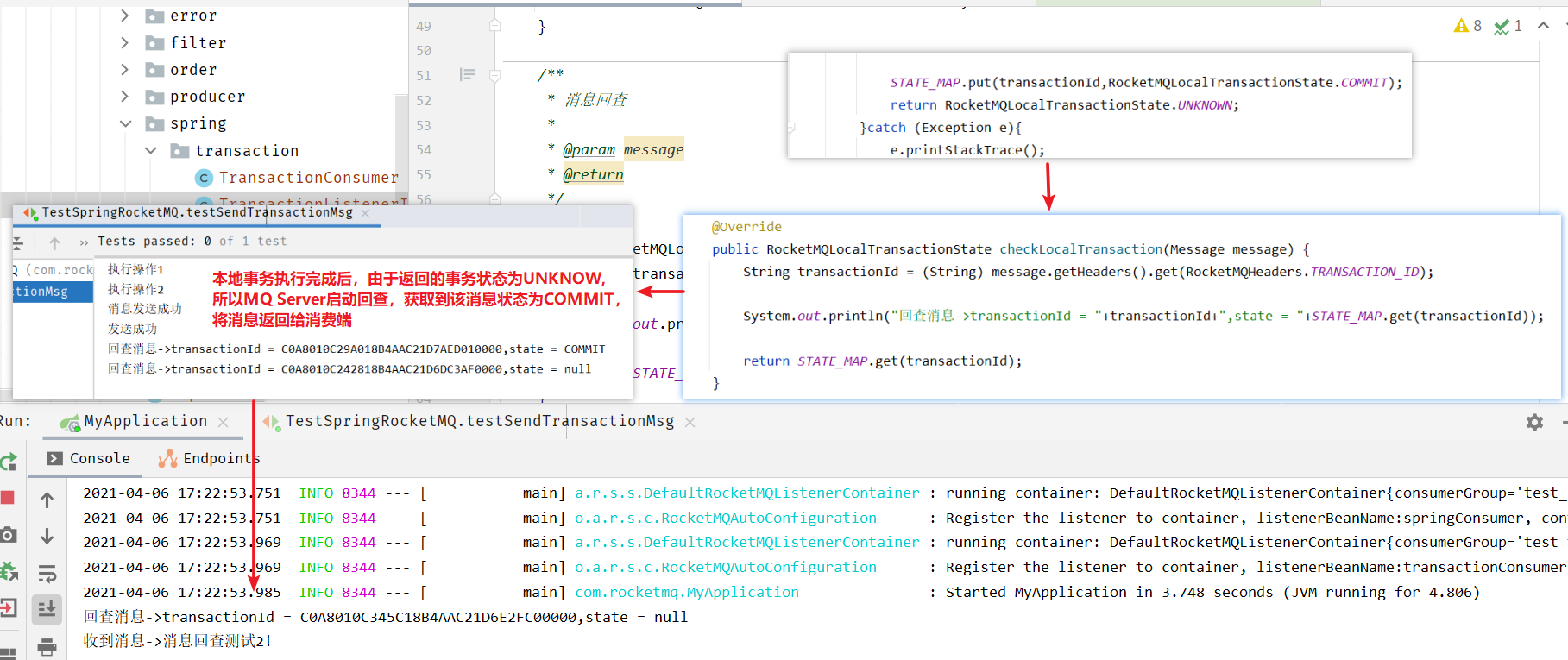
分布式消息系统 RocketMQ概念,用途,特性安装RocketMQ掌握RocketMQ的api使用对producer、consumer进行详解了解RocketMQ的存储特点 简介及相关概念JavaAPISpringBoot整合RocketMQ消息的顺序收发消息系统的事务、存储、重试策略消息系统的集群 RocketMQ R…...
36 UnitTest框架 - 参数化
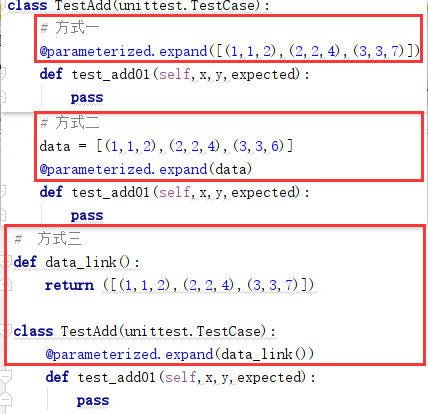
目录 一、参数化环境准备 1、方式一:在终端(cmd)安装parameterized 2、方式二:在Pycharm中安装parameterized 二、参数化 1、什么事参数化? 2、参数化引入案例 (1)需求 (2&a…...
 事件循环)
Qt源码阅读(四) 事件循环
事件系统 文章为本人理解,如有理解不到位之处,烦请各位指正。 文章目录事件系统什么是事件循环?事件是如何产生的?sendEventpostEvent事件是如何处理的?事件循环是怎么遍历的?事件过滤器event夹带私货时间Q…...

银行数字化转型导师坚鹏:银行数字化领导力提升之道
银行数字化领导力提升之道 ——融合中西智慧,践行知行合一思想,实现知行果合一 课程背景: 很多银行存在以下问题:不知道如何领导数字员工?不清楚银行数字化领导力模型的内涵?不知道如何开展银行数字化…...

Vue2 -- 自定义单选内容的单选框组件
自定义单选内容的单选框组件 之前做的一个项目,在项目中有一个关于人员权限分配的功能,给人员指定各个模块的权限信息,分为 write 可写权限read 可读权限none 没有权限 项目要求画面中只显示 W R 两个按钮控制指定权限信息,都不…...

让PyTorch训练速度更快,你需要掌握这17种方法
掌握这 17 种方法,用最省力的方式,加速你的 Pytorch 深度学习训练。近日,Reddit 上一个帖子热度爆表。主题内容是关于怎样加速 PyTorch 训练。原文作者是来自苏黎世联邦理工学院的计算机科学硕士生 LORENZ KUHN,文章向我们介绍了在…...

LeetCode-309. 最佳买卖股票时机含冷冻期
目录题目思路动态规划题目来源 309. 最佳买卖股票时机含冷冻期 题目思路 每天最多只可能有三种状态中的一种 0表示当前处于买入状态(持有股票) 1表示当前处于卖出状态(不持有股票) 2表示当前处于冷冻状态 设dp[i][j]表示i - 1天状态为j时所拥有的最大现金 dp[i][0] Math.ma…...
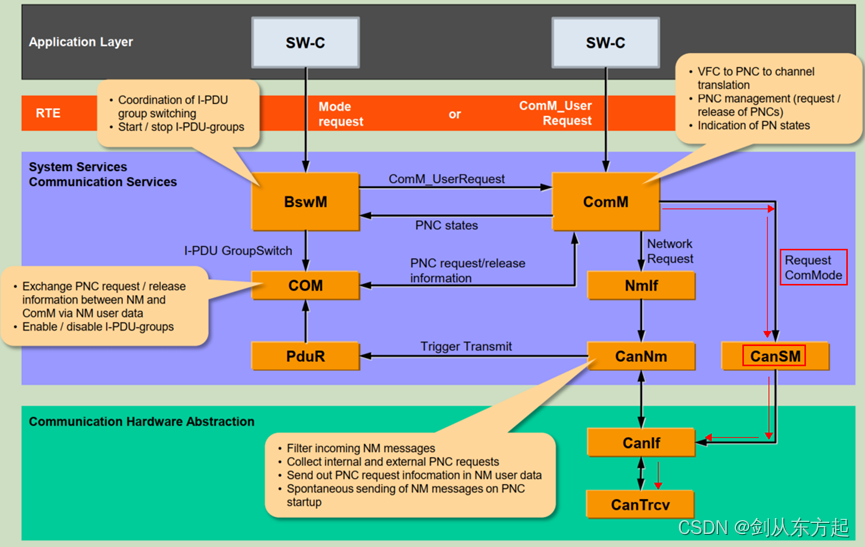
AUTOSAR知识点Com(七):CANSM初认知
目录 1、概述 2、CanSM主要做什么 2.1、CAN控制器状态管理 2.2、CAN收发器状态管理 2.3、Busoff检测 1、概述 CANSM(Controller Area Network State Manager)是AUTOSAR(Automotive Open System Architecture)标准中的一个模块…...

递归:斐波那契数列、递归实现指数型枚举、递归实现排列型枚举
递归:O(2^n) 调用自己 例题及代码模板: 斐波那契数列 输入一个整数 n ,求斐波那契数列的第 n 项。 假定从 0 开始,第 0 项为 0。 数据范围 0≤n≤39 样例 输入整数 n5 返回 5 #include <iostream> #include <cstring&g…...

oracle模糊查询时字段内容包含下划线的解决办法
最近项目中遇到一个关于模糊查询问题。表tabA中的字段name的值有下划线的情况,在模糊查询时发现查询的记录不对。 表的结构 表名:tabA id name sex 1 test_601 1 2 test_602 2 3 test16 1 4 t…...

C++:explicit关键字
C中的explicit关键字只能用于修饰只有一个参数的类构造函数,它的作用是表明该构造函数是显示的,而非隐式的,跟它相对应的另一个关键字是implicit,意思是隐藏的,类构造函数默认情况下即声明为implicit(隐式)。那么显示声…...

【C5】bmc wtd,post
文章目录1.bmc_wtd_cpld:syscpld.c中wd_en和wd_kick节点对应寄存器,crontab,FUNCNAME2.AST芯片WDT切换主备:BMC用WDT2作为主备切换的控制器2.1 AC后读取:bmc处于主primary flash(设完后:实际主&…...
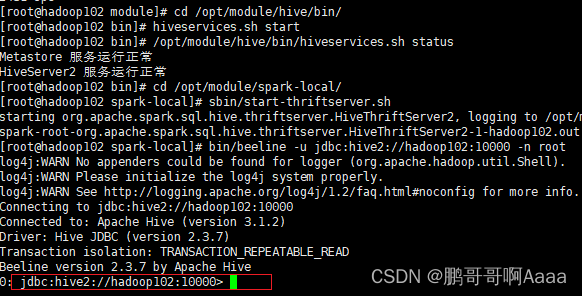
200.Spark(七):SparkSQL项目实战
一、启动环境 需要启动mysql,hadoop,hive,spark。并且能让spark连接上hive(上一章有讲) #启动mysql,并登录,密码123456 sudo systemctl start mysqld mysql -uroot -p#启动hive cd /opt/module/ myhadoop.sh start#查看启动情况 jpsall#启动hive cd /opt/module/hive/…...
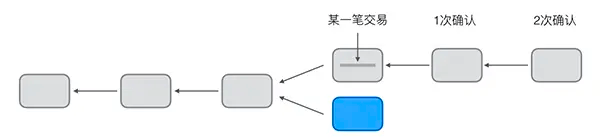
区块链系统:挖矿原理
在比特币的P2P网络中,有一类节点,它们时刻不停地进行计算,试图把新的交易打包成新的区块并附加到区块链上,这类节点就是矿工。因为每打包一个新的区块,打包该区块的矿工就可以获得一笔比特币作为奖励。所以,…...

【博弈】【清华冬令营2018模拟】取石子
写完敢说全网没有这么详细的题解了。 注意:题解长是为了方便理解,所以读起来速度应该很快。 题目描述 有 nnn 堆石子,第 iii 堆有 xix_ixi 个。 AliceAliceAlice 和 BobBobBob 轮流去石子(先后手未定), …...
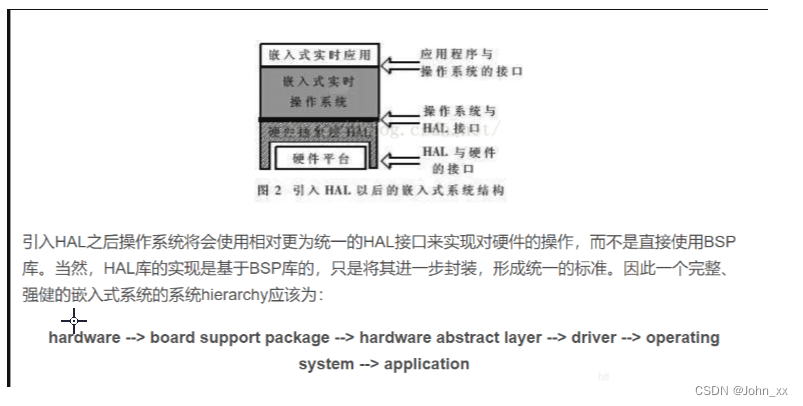
嵌入式:BSP的理解
BSP概念总结BSP定义BSP的特点BSP的主要工作BSP在嵌入式系统和Windowsx系统中的不同BSP和PC机主板上的BIOS区别BSP与 HAL关系嵌入式计算机系统主要由 硬件层,中间层,系统软件层和应用软件层四层组成。硬件层:包含CPU,存储器(SDRAM&…...
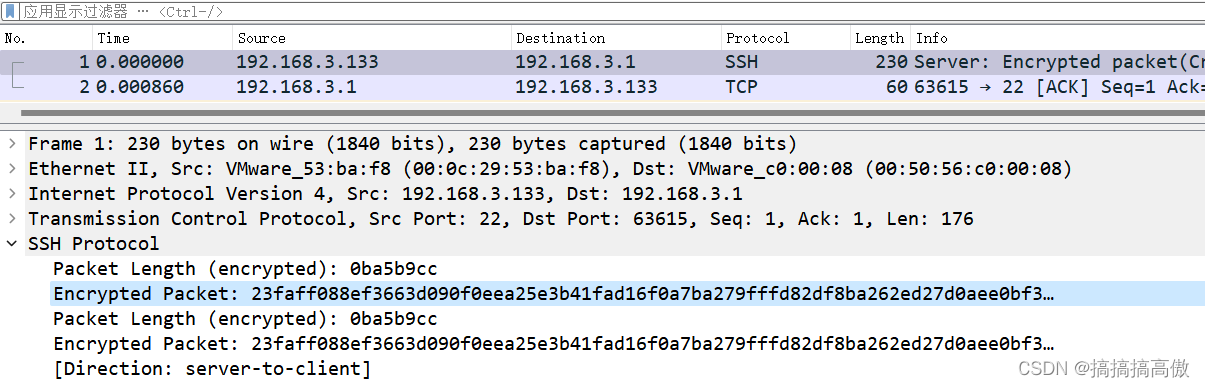
Linux主机Tcpdump使用-centos实例
1、安装前系统信息 ifconfig查看系统网络接口情况。这里可以看到3个interface,ens160是正常使用的网口,lo是主机的loopback地址127.0.0.1。另外,由于centos安装在虚拟主机上,virbr0是KVM默认创建的一个Bridge,其作用是为连接其上的…...
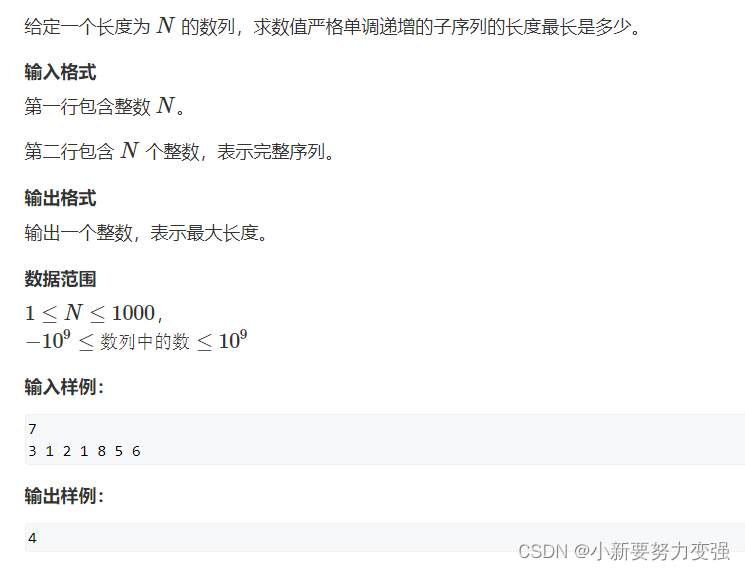
线性DP——AcWing 898. 数字三角形、AcWing 895. 最长上升子序列
AcWing 898. 数字三角形 1.题目 898. 数字三角形 2.思路 DP问题首先考虑状态转移方程,定义一个集合f ( i , j) ,表示从第一个数字(1,1)走到第 i行,第 j列(i , j)的所有方案的集合,…...
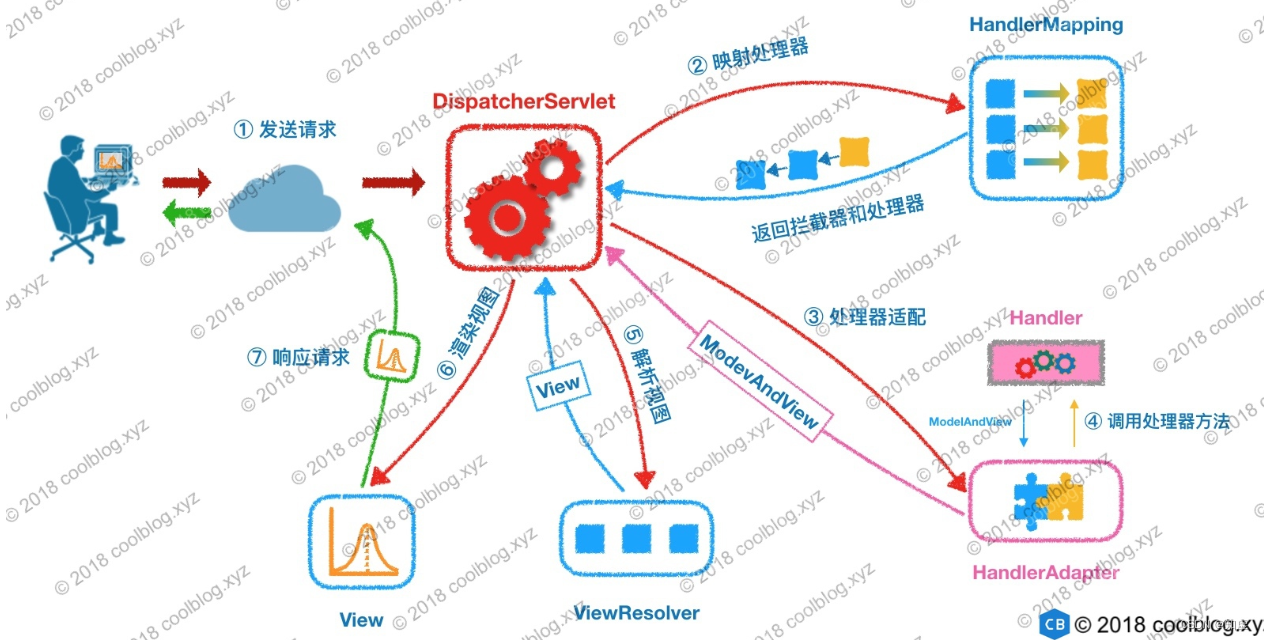
SpringMVC
SpringMVC配置 引入Maven依赖 (springmvc)web.xml配置DispatcherServlet配置 applicationContext 的 MVC 标记开发Controller控制器 几点注意事项: 在web.xml中 配置<load-on-startup> 0 </load-on-startup> 会自动创建Spring…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

Qt 按钮类控件(Push Button 与 Radio Button)(1)
文章目录 Push Button前提概要API接口给按钮添加图标给按钮添加快捷键 Radio ButtonAPI接口性别选择 Push Button(鼠标点击不放连续移动快捷键) Radio Button Push Button 前提概要 1. 之前文章中所提到的各种跟QWidget有关的各种属性/函数/方法&#…...
