图神经网络池化方法
图神经网络池化方法
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 图神经网络池化方法
- 前言
- 一、扁平图池化
- 二、分层图池化
- 1.节点聚类池化
- 2.节点丢弃池化
- 参考文献
前言
图池化操作根据其池化策略的差异,可细分为扁平图池化和分层图池化两大类:
- 如下图(a)所示,扁平图池化(Flat Graph Pooling)技术通过一步操作对图中节点进行降维或聚合,直接获得整体图的表征。这一过程旨在快速提取出图的全局表示,适用于那些需要快速获得全局图表示的场景。
- 如下图(b)所示,分层图池化(Hierarchical Graph Pooling)则通过一个分阶段的策略来逐步简化图结构,即在图的每一层上通过减少节点的数量,逐步构建图的更高层次的表征。
这种分层的方法允许模型在每一步中细致地捕获和保留图的重要结构信息,适合于需要深层次理解图结构特征的复杂任务。两种池化策略各有优势,选择哪一种依赖于特定任务的需求和目标。

一、扁平图池化
扁平图池化是一种图池化策略,其特点在于对图中的节点进行一次性的降维或聚合操作,从而简化图的整体结构并直接提取出图级别的特征表示。这种池化技术的核心在于直接从整个图中聚合信息,而非通过对图结构进行多层递归简化来实现。该方法的主要优势在于其简单直接的处理方式,能够在不引入额外计算复杂度的情况下,为下游任务提供有力的图级别特征。
对于给定的图 G = { A , X } \mathcal{G}=\{A,X\} G={A,X},其中 A A A 是图的邻接矩阵,用于描述图中各个节点之间的连接情况; X X X是节点的特征矩阵,包含了与每个节点相关的属性或特征信息。扁平图池化可以定义为如下过程:
X ( l ) = GNN ( l ) ( G ) , h G = Pool f l a t ( X ( l ) ) , X^{(l)}=\text{GNN}^{(l)}(\mathcal{G}),\\ h_{\mathcal{G}}=\text{Pool}_{flat}(X^{(l)}), X(l)=GNN(l)(G),hG=Poolflat(X(l)),
这里GNN指的是任意图神经网络,经过 l l l 层的图神经网络之后,得到图中全部节点的特征表示矩阵 X ( l ) X^{(l)} X(l)。 h G h_{\mathcal{G}} hG表示经过图池化后得到的图最终表征向量, Pool f l a t \text{Pool}_{flat} Poolflat表示扁平图池化函数,它需要具备以下两个特点:1)对于不同大小的输入图,输出固定大小的图表示;2)在输入图的节点顺序改变时,输出相同的表示。基于以上讨论,几种最常见的扁平池化方法是均值池化(Mean-Pool)、最大值池化(Max-Pool)和求和池化(Sum-Pool),即通过所有节点特征取平均、求最大值以及求和得到。
近期,研究者们通过融入注意力机制,赋予了模型在构建图级别表示时更大的适应性和灵活性。这种机制允许模型动态地为每个节点分配权重,从而更细致地揭示节点间的相对重要性。例如,一些研究工作[1-3]在他们的池化框架中嵌入了软注意力机制,旨在精确地捕捉并表达节点之间的微妙关系。此外,Bai等人[4]采纳了一种创新策略,将卷积神经网络应用于已排序的节点表示上,通过这种方式,他们能够依据节点特征的排序顺序来挖掘图的关键信息。与传统依赖于节点特征一阶统计信息的方法不同,Wang等人[5]引入了二阶池化(Second-order Pooling,SOPool),其主要思想是利用节点特征的二次方来提取图的二阶统计信息。这种方法通过捕获图节点特征的相互关系,能够提供更丰富和深入的图表示,从而增强模型对图结构复杂性的理解和表达能力。
这里,我们向大家推荐我们组的工作,DKEPool [6](Distribution Knowledge Embedding for Graph Pooling)通过引入分布信息的表征,其也是一种扁平的图池化方法,在确保不丢失任何节点信息的前提下,使用非线性的高斯分布信息去拟合非欧几何的图结构数据,从而提升图结构数据的表征能力以及相应的分类效果。
二、分层图池化
分层池化方法的目的是通过将图迭代地粗化为更小尺寸的新图,以保留图的层次结构信息。根据粗化图的方式,分层池化大致可以分为节点聚类池化、节点丢弃池化以及其他类型的池化。节点聚类池化和节点丢弃池化方法都对原始图结构进行了修改,但它们各自采用了不同的策略来保留图的关键信息。节点聚类池化通过合并节点来形成新的节点结构,这样不仅保留了原始图的信息,还在一定程度上维护了图的结构完整性。相反,节点丢弃池化方法着重于抛弃不重要的节点,仅保留那些被认为是图核心结构的一小部分节点。值得注意的是,尽管分层池化方法在概念上设计为在多个层次上粗化图结构,分层池化方法在技术上仍然使用扁平池化方法来获得粗化后图的表示。
1.节点聚类池化
节点聚类池[7-10]将图池化视作一个节点聚类问题,其核心思想是将图中的节点根据相似性或其他准则映射到若干个簇中。
为了全面阐释这种方法,这里提供了一个通用的分解框架,主要由以下两个主要模块来实施节点聚类池化:1)簇分配矩阵(Cluster Assignment Matrix, CAM)生成器:给定一个输入图,CAM根据输入图计算节点到簇的分配,这一步骤可能产生每个节点到簇的硬/软分配。2) 图粗化(Graph Coarsening)模块:该模块利用上述簇分配矩阵,通过提取新的特征表示和更新邻接矩阵,转换原始图为一个粗化的简化版本。这一粗化过程旨在保留图的核心结构特性,同时减小了图的规模,从而在保持图的关键信息的同时提高了计算效率。
对于给定的图 G = { A , X } \mathcal{G}=\{A,X\} G={A,X},其中 A A A 是图的邻接矩阵, X X X是节点的特征矩阵。节点聚类池化过程可以如下表述:
C ( l ) = CAM ( X ( l ) , A ( l ) ) , X ( l + 1 ) , A ( l + 1 ) = Coarsen ( X ( l ) , A ( l ) , C ( l ) ) , C^{(l)}=\text{CAM}(X^{(l)},A^{(l)}),\\ X^{(l+1)},A^{(l+1)}=\text{Coarsen}(X^{(l)},A^{(l)},C^{(l)}), C(l)=CAM(X(l),A(l)),X(l+1),A(l+1)=Coarsen(X(l),A(l),C(l)),
其中, CAM \text{CAM} CAM 和 Coarsen \text{Coarsen} Coarsen 分别指的簇矩阵生成和图粗化操作。 CAM \text{CAM} CAM 以第 l l l 层的邻接矩阵和节点特征矩阵为输入,输出第 l l l 层的簇矩阵 C ( l ) ∈ R n l × n l + 1 C^{(l)}\in\mathbb{R}^{n_l\times n_{l+1}} C(l)∈Rnl×nl+1, n l n_l nl 是第 l l l 层的节点个数。 Coarsen \text{Coarsen} Coarsen 以第 l l l 层邻接矩阵、节点特征矩阵和簇矩阵为输入,输出第 l + 1 l+1 l+1 层的邻接矩阵和节点特征矩阵。
2.节点丢弃池化
节点丢弃池化[11-16]策略通过采用可学习的评分机制来识别并剔除相对不重要的节点,有效地简化图结构。
为了深入理解节点丢弃池化的过程,我们构建了一个由三个独立模块组成的通用框架,旨在清楚地说明其工作原理:1)分数生成器(Score Generator):针对输入图的每个节点,该模块负责生成一个反映节点重要性的分数。(2)节点选择器(Node Selector):根据生成的重要性分数,此模块负责挑选出分数最高的前 k k k个节点。(3)图粗化(Graph Coarsen):利用所选节点来构建一个新的粗化图,即新的特征矩阵和邻接矩阵。通过这个分模块的框架,节点丢弃池化过程的每个环节都被结构化地展现出来,,从而为优化图结构提供了清晰的路径。
对于给定的图 G = { A , X } \mathcal{G}=\{A,X\} G={A,X},其中 A A A 是图的邻接矩阵, X X X 是节点的特征矩阵。节点丢弃池化过程可以如下表述:
S ( l ) = Score ( X ( l ) , A ( l ) ) , idx ( l + 1 ) = Top-k ( S ( l ) ) , X ( l + 1 ) , A ( l + 1 ) = Coarsen ( X ( l ) , A ( l ) , S ( l ) , idx ( l + 1 ) ) , S^{(l)}=\text{Score}(X^{(l)},A^{(l)}),\\ \text{idx}^{(l+1)}=\text{Top-k}(S^{(l)}),\\ X^{(l+1)},A^{(l+1)}=\text{Coarsen}(X^{(l)},A^{(l)},S^{(l)},\text{idx}^{(l+1)}), S(l)=Score(X(l),A(l)),idx(l+1)=Top-k(S(l)),X(l+1),A(l+1)=Coarsen(X(l),A(l),S(l),idx(l+1)),
这里,函数Score,Top-k和Coarsen分别表示的是分数生成器,节点选择器和图粗化。
Score以第 l l l层的邻接矩阵和节点特征矩阵为输入,输出 S l ∈ R n l × 1 S^{l}\in \mathbb{R}^{{n_l}\times 1} Sl∈Rnl×1 表示节点重要性分数,其中 n l n_l nl是第 l l l层的节点个数。 Top-k将分数从大到小排列并提供 S l S^{l} Sl中最大的 k k k个值的索引, idx ( l + 1 ) \text{idx}^{(l+1)} idx(l+1)指示新图中保留节点的索引。与节点聚类池化中Coarsen不同,这里在以第 l l l 层邻接矩阵、节点特征矩阵和簇矩阵为输入的同时,需要额外使用 idx ( l + 1 ) \text{idx}^{(l+1)} idx(l+1) 信息。
参考文献
- Fan X, Gong M, Xie Y, et al. Structured self-attention architecture for graph-level representation learning[J]. Pattern Recognition, 2020, 100: 107084.
- Itoh T D, Kubo T, Ikeda K. Multi-level attention pooling for graph neural networks: Unifying graph representations with multiple localities[J]. Neural Networks, 2022, 145: 356-373.
- Yunsheng B, Ding H, Qiao Y, et al. Unsupervised inductive graph-level representation learning via graph-graph proximity[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. 1988, 1994.
- Bai L, Jiao Y, Cui L, et al. Learning graph convolutional networks based on quantum vertex information propagation[J]. IEEE Transactions on Knowledge and Data Engineering, 2021, 35(2): 1747-1760.
- Wang Z, Ji S. Second-order pooling for graph neural networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 45(6): 6870-6880.
- Chen K, Song J, Liu S, et al. Distribution Knowledge Embedding for Graph Pooling[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(08): 7898-7908.
- Khasahmadi A H, Hassani K, Moradi P, et al. Memory-Based Graph Networks[C]//International Conference on Learning Representations.
- Yuan H, Ji S. Structpool: Structured graph pooling via conditional random fields[C]//Proceedings of the 8th international conference on learning representations. 2020.
- Liu N, Jian S, Li D, et al. Hierarchical adaptive pooling by capturing high-order dependency for graph representation learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2021, 35(4): 3952-3965.
- Wu J, Chen X, Xu K, et al. Structural entropy guided graph hierarchical pooling[C]//International conference on machine learning. PMLR, 2022: 24017-24030.
- Lee J, Lee I, Kang J. Self-attention graph pooling[C]//International conference on machine learning. pmlr, 2019: 3734-3743.
- Ranjan E, Sanyal S, Talukdar P. Asap: Adaptive structure aware pooling for learning hierarchical graph representations[C]//Proceedings of the AAAI conference on artificial intelligence. 2020, 34(04): 5470-5477.
- Zhang L, Wang X, Li H, et al. Structure-feature based graph self-adaptive pooling[C]//Proceedings of The Web Conference 2020. 2020: 3098-3104.
- Ma Z, Xuan J, Wang Y G, et al. Path integral based convolution and pooling for graph neural networks[J]. Advances in Neural Information Processing Systems, 2020, 33: 16421-16433.
- Gao H, Liu Y, Ji S. Topology-aware graph pooling networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(12): 4512-4518.
- Shu D W, Kwon J. Hierarchical bidirected graph convolutions for large-scale 3-D point cloud place recognition[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023.
相关文章:

图神经网络池化方法
图神经网络池化方法 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 图神经网络池化方法前言一、扁平图池化二、分层图池化1.节点聚类池化2.节点丢弃池化 参考文献 前言 图池化操作根据其池化策略的差异ÿ…...

小琳AI课堂:确保大语言模型安全的八大策略--从数据隐私到用户教育
大家好,这里是小琳AI课堂。今天我们深入探讨如何保证大语言模型的安全,这可是关系到我们每个人哦!🔐 首先,我们要明白,保证大语言模型的安全,需要从多个方面入手,确保模型在技术、法…...

Python 数学建模——高斯核密度估计
文章目录 前言原理代码实例scipy 实现seaborn 实现 前言 高斯核密度估计本是一种机器学习算法,在数学建模中也可以发挥作用。本文主要讨论用它来拟合变量的概率密度,获得概率密度函数 f ( x ) f(x) f(x)。 原理 已知一个连续型随机变量 X X X 的一系列…...

Flink+Spark相关记录
FlinkSpark相关记录 FlinkSQL Flink Streaming的一些点覆写RichSource、RichSink、RichMap 1.Source自动负载均衡,CDC源端加入一个全局调控的节点监控流量流速 2.Sink并发写入 3.Map与Iterator与增量迭代等用法关于Checkpoint几个用法 1.提交Commit至目的端数据库 2…...

2023 hnust 湖科大 毕业实习 报告+实习鉴定表
2023 hnust 湖科大 毕业实习 报告实习鉴定表 岗位 IT公司机房运维 实习报告 实习鉴定表 常见疑问 hnust 湖科大 毕业实习常见问题30问(2021 年7月,V0.9)-CSDN博客时间:大四开学第三四周毕业实习23年是企业(黑马&am…...

ConflictingBeanDefinitionException | 运行SpringBoot项目时报错bean定义冲突解决方案
具体报错: Caused by: org.springframework.context.annotation.ConflictingBeanDefinitionException: Annotation-specified bean name ‘CommissionMapperImpl’ for bean class [com.xxx.mapper.carrier.CommissionMapperImpl] conflicts with existing, non-co…...
【2024版】)
如何切换淘宝最新镜像源(npm)【2024版】
在使用 Node.js 和 npm 进行开发时,大家通常会遇到 npm 源速度较慢的问题。特别是当你需要安装大量依赖时,npm 官方源的速度可能不尽如人意。幸运的是,淘宝提供了一个更快速的 npm 镜像源,可以让你更快地下载和安装包。本文将介绍…...
YoloV10改进策略:Block改进|PromptIR(NIPS‘2023)|轻量高效,即插即用|(适用于分类、分割、检测等多种场景)
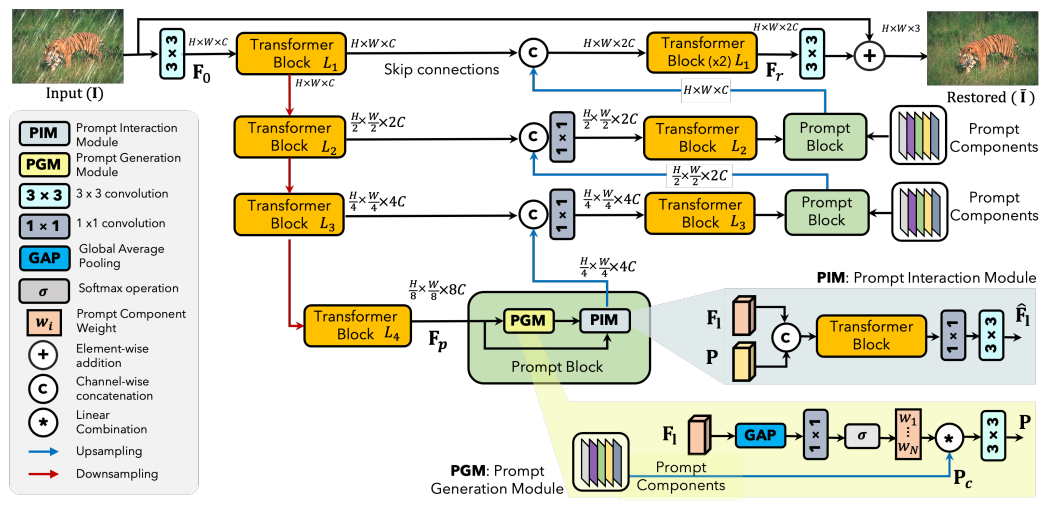
文章目录 摘要代码详解如何在自己的论文中描述改进方法测试结果总结摘要 本文使用PromptIR框架中的PGM模块来改进YoloV10。PGM(Prompt Generation Module)模块是PromptIR框架中的一个重要组成部分,主要负责生成输入条件化的提示(prompts)。这些提示是一组可学习的参数,它…...

使用rust自制操作系统内核
一、系统简介 本操作系统是一个使用rust语言实现,基于32位的x86CPU的分时操作系统。 项目地址(求star):GitHub - CaoGaorong/os-in-rust: 使用rust实现一个操作系统内核 详细文档:自制操作系统 语雀 1. 项目特性 …...

Flink难点和高阶面试题:Flink的状态管理机制如何保证数据处理的准确性和完整性
1 Flink状态管理机制核心要素 1.1 内置状态后端 在Apache Flink中,状态管理机制是确保数据处理准确性与完整性的关键环节。其核心在于灵活且高效的状态后端,这些后端负责在分布式环境中安全地存储和访问状态数据。Flink提供了多种内置状态后端,其中RocksDB和内存状态后端最…...

【激励广告带来的广告收入与用户留存率的双重提升】
激励广告带来的广告收入与用户留存率的双重提升 ) 随着移动应用市场的竞争加剧,如何通过广告变现成为众多开发者关注的焦点。其中,激励广告(Rewarded Ads)凭借其用户友好、互动性强等特点,逐渐成为开发者的首选。那些…...

指针和引用;内联函数和普通函数
1. 指针和引用 1.1 定义和性质区别 指针是一个变量,只不过这个变量存储的是一个地址,指向内存的一个存储单元;而引用跟原来的变量实质上是同一个东西,只不过是原变量的一个别名而已。可以有const指针,常量指针可以改…...

简单题67.二进制求和 (java)20240919
题目描述: Java: class Solution {public String addBinary(String a, String b) {StringBuilder result new StringBuilder();int i a.length()-1;int j b.length()-1;int carry 0; //记录进位信息while(i>0 || j>0 || carry!0){int sum ca…...

DDD的主要流程
DDD 开发流程分为模型的建立和模型的实现两大部分,接下来是具体的流程讲解以及流程图。 1. 模型的建立 捕获行为需求:在这一阶段,团队要识别系统中需要完成的任务、操作流程、功能需求以及每个功能由谁操作、会产生什么结果。我们可以通过 …...

linux驱动开发-设备树
设备树的历史背景 背景: 在早期的嵌入式系统中,硬件配置信息通常硬编码在内核源码中,这导致了内核代码的冗长和难以维护。 为了解决这个问题,设备树(Device Tree)被引入,使得硬件描述与内核代…...

数据结构——二叉树堆的专题
1.堆的概念及结构 如果有一个关键码的集合K {K0 ,K1 ,K2 ,K3…,K(N-1) },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki < K2*i1且 Ki<K2*i2 ) i 0&#…...

【C语言零基础入门篇 - 7】:拆解函数的奥秘:定义、声明、变量,传递须知,嵌套玩转,递归惊艳
文章目录 函数函数的定义与声明局部变量和全局变量、静态变量静态变量和动态变量函数的值传递函数参数的地址传值 函数的嵌套使用函数的递归调用 函数 函数的定义与声明 函数的概念:函数是C语言项目的基本组成单位。实现一个功能可以封装一个函数来实现。定义函数的…...

ClickHouse在AI领域的结合应用
文章目录 引言1.1 人工智能与大数据的融合1.2 ClickHouse在大数据平台中的地位2.1 BI与AI的融合从传统BI到智能BIAI赋能BI融合的优势实际应用案例 2.2 异构数据处理的重要性数据多样性的挑战异构数据处理的需求技术实现实际应用案例 2.3 向量检索与AIOps技术向量检索的背景AIOp…...

git push出错Push cannot contain secrets
报错原因: 因为你的代码里面包含了github token明文信息,github担心你的token会泄漏,所以就不允许你推送这些内容。 解决办法: 需要先把代码里面的github token信息删除掉,并且删掉之前的历史提交,只要包…...
OpenAI 的最强模型 o1 的“护城河”失守?谷歌 DeepMind 早已揭示相同原理
发布不到一周,OpenAI 的最新模型 o1 的“护城河”似乎已经失守。 近日,有人发现谷歌 DeepMind 早在今年 8 月发表的一篇论文,揭示了与 o1 模型极其相似的工作原理。 这项研究指出,在模型推理过程中增加测试时的计算量,…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
