python 山峦图
效果:

代码:
import matplotlib.pyplot as plt
import numpy as npdef mountain_plot(data_dict, colors=None):if colors is None:colors = get_colors_from_map(len(data_dict), "Spectral")x = list(data_dict.keys())# Y轴位置y_positions = [2 * i for i in range(len(x))]# 创建图形fig, axs = plt.subplots(figsize=(8, 12))# 为每个月绘制核密度曲线,并水平错开显示for i, month in enumerate(list(data_dict.keys())):# 核密度估计density, bins = np.histogram(data_dict[month], bins=30, density=True)bins = 0.5 * (bins[1:] + bins[:-1]) # 转换为 bin 的中心# 每个月份的曲线位置偏移axs.fill_between(bins, y_positions[i] + density, y_positions[i], facecolor=colors[i], alpha=0.7)axs.plot(bins, y_positions[i] + density, color=colors[i], lw=1.5)# 设置月份作为Y轴标签axs.set_yticks(y_positions)axs.set_yticklabels(x)# 添加横轴的网格线axs.grid(axis='y', linewidth=1, color='gray', alpha=0.2)# 去掉边框线axs.spines['top'].set_visible(False)axs.spines['bottom'].set_visible(False)axs.spines['right'].set_visible(False)axs.spines['left'].set_visible(False)# 显示图像plt.tight_layout()plt.show()if __name__ == '__main__':# 模拟数据生成函数,基于正态分布def generate_trend_data(size=1000):np.random.seed(0)# 前半段平稳trend = np.linspace(0, 0.3, size // 2)# 后半段波动较大trend = np.concatenate([trend, np.random.normal(0.1, 0.5, size // 2)])return trenddef generate_normal_data(mean, std=1.2, size=1000):np.random.seed(6) # 固定随机数种子return np.random.normal(mean, std, size)# 月份months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']# 为每个月生成不同的正态分布数据data_dict = {}for i in range(6):data_dict[months[i]] = generate_normal_data(i * 2) / 10for i in range(6, 12):data_dict[months[i]] = generate_normal_data((11 - i) * 2) / 10mountain_plot(data_dict)相关文章:

python 山峦图
效果: 代码: import matplotlib.pyplot as plt import numpy as npdef mountain_plot(data_dict, colorsNone):if colors is None:colors get_colors_from_map(len(data_dict), "Spectral")x list(data_dict.keys())# Y轴位置y_positions …...

Open3D:3D数据处理与可视化的强大工具
创作不易,您的打赏、关注、点赞、收藏和转发是我坚持下去的动力! Open3D算法框架简介 Open3D是一个开源的3D数据处理库,旨在为3D数据提供高效、易用的计算和可视化工具。它支持多种3D数据格式,例如点云、网格、RGB-D图像等&…...

YOLOv8改进系列,YOLOv8的Neck替换成AFPN(CVPR 2023)
摘要 多尺度特征在物体检测任务中对编码具有尺度变化的物体非常重要。多尺度特征提取的常见策略是采用经典的自上而下和自下而上的特征金字塔网络。然而,这些方法存在特征信息丢失或退化的问题,影响了非相邻层次的融合效果。一种渐进式特征金字塔网络(AFPN),以支持非相邻…...

BitLocker硬盘加密的详细教程分享
硬盘加密是将数据转换为一种只有授权用户才能读取的形式。通过使用加密算法,硬盘上的数据在存储时被加密,只有输入正确的密钥或密码才能解密和访问这些数据。 硬盘加密的重要性 数据是现代社会的重要资产,保护这些数据免受非法访问和窃取至关…...

YOLOv8的GPU环境搭建方法
首先说明这个环境搭建教程是基于电脑已经安装好CUDA和CUDNN的情况下,去搭建能够正确运行YOLOv8代码的Pytorch的GPU版本。具体安装方法可见:最适合新手入门的CUDA、CUDNN、Pytorch安装教程_cuda安装-CSDN博客 第一步:需要在cmd中创建虚拟环境c…...

JZ2440下载后设置NAND启动文件系统
(一)下载 (二)设置根文件系统NAND FLASH启动 set bootargs noinitrd root/dev/mtdblock3 init/linuxrc consolettySAC0...

AI绘画与摄影新纪元:ChatGPT+Midjourney+文心一格 共绘梦幻世界
文章目录 一、AI艺术的新时代二、ChatGPT:创意的引擎与灵感的火花三、Midjourney:图像生成的魔法与技术的奇迹四、文心一格:艺术的升华与情感的共鸣五、融合创新:AI绘画与摄影实战的无限可能六、应用场景与实践案例AI艺术的美好未…...

金手指设计
"MCP6294"。是一个轨到轨, 带宽为 10MHz 的 低功耗放大器. 对LM358测量 10MHz 范围内的频率特性,在 8MHz 左右,输出相移超过了 180。MCP6294的频率特性,则显示在 10MHz 运放相移之后 100左右。 对比两个运放的频率特性ÿ…...

Chainlit集成LlamaIndex并使用通义千问模型实现AI知识库检索网页对话应用增强版
前言 之前使用Chainlit集成LlamaIndex并使用通义千问大语言模型的API接口,实现一个基于文档文档的网页对话应用。 可以点击我的上一篇文章《Chainlit集成LlamaIndex并使用通义千问模型实现AI知识库检索网页对话应用》 查看。 本次针对上一次的代码功能进一步的完善…...

详解c++菱形继承和多态---下
菱形继承 #include<iostream>using namespace std; class Animal { public:int m_Age; }; class Sheep : public Animal {}; class Tuo : public Animal {}; class SheepTuo : public Sheep, public Tuo {}; void test() {SheepTuo st;st.Sheep::m_Age 18;st.Tuo::m_Age…...

python学习笔记目录
基于windows下docker安装HDDM-CSDN博客 在python中安装HDDM-CSDN博客(这个办法没安装成功)...

非结构化数据中台架构设计最佳实践
在数据驱动的时代背景下,非结构化数据已成为企业决策和运营的重要支撑。非结构化数据中台作为企业数据管理和分析的核心平台,其架构设计对于数据的高效利用和业务的快速发展至关重要。本文将探讨非结构化数据中台架构设计的最佳实践,旨在为企…...

鹏鼎控股社招校招入职SHL综合能力测评:高分攻略及真题题库解析答疑
鹏鼎控股(深圳)股份有限公司,成立于1999年4月29日,是一家专注于印制电路板(PCB)的设计、研发、制造与销售的高新技术企业。公司总部位于中国广东省深圳市,并在全球多个地区设有生产基地和服务中…...
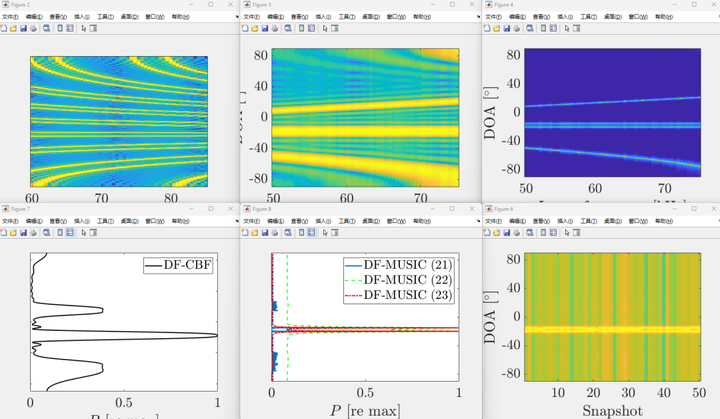
【测向定位】差频MUSIC算法DOA估计【附MATLAB代码】
微信公众号:EW Frontier QQ交流群:554073254 摘要 利用多频处理方法,在不产生空间混叠的情况下,估计出高频区域平面波的波达方向。该方法利用了差频(DF),即两个高频之间的差。这使得能够在可…...

智能车镜头组入门(四)元素识别
元素识别是摄像头部分中难度最大的一部分,也是我花时间最长的一部分,前前后后画了很长时间,最后还是勉勉强强完成了。 基础的元素识别主要有两个:十字,圆环,和斑马线。十字要求直行,圆环需要进…...

Java键盘输入语句
编程输入语句 1.介绍:在编程中,需要接受用户输入的数据,就可以使用键盘输入语句来获取。 2.步骤: 1)导入该类的所在包,java.util.* 2)创建该类对象(声明变量) 3)调用里面的功能 3…...

【读书笔记-《30天自制操作系统》-22】Day23
本篇内容比较简单,集中于显示问题。首先编写了应用程序使用的api_malloc,然后实现了在窗口中画点与画线的API与应用程序。有了窗口显示,还要实现关闭窗口的功能,于是在键盘输入API的基础上实现了按下按键关闭窗口。最后发现用上文…...
)
C++学习笔记(33)
三十五、栈 示例: #include <iostream> using namespace std; typedef int ElemType; // 自定义链栈的数据元素为整数。 struct SNode // 链栈的结点。 { ElemType data; // 存放结点的数据元素。 struct SNode* next; // 指向下一个结点的指针。 }; // 初始化…...

智谱清影 -CogVideoX-2b-部署与使用,带你揭秘生成6s视频的极致体验!
文章目录 1 效果展示2 CogVideoX 前世今生3 CogVideoX 部署实践流程3.1 创建丹摩实例3.2 配置环境和依赖3.3 模型与配置文件3.4 运行4 遇到问题 1 效果展示 A street artist, clad in a worn-out denim jacket and a colorful bandana, stands before a vast concrete wall in …...

探索Java中的设计模式:原则与实例
探索Java中的设计模式:原则与实例 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将深入探讨Java中的设计模式,包括一些关键的设计原则和具体的实例。设计…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

(12)-Fiddler抓包-Fiddler设置IOS手机抓包
1.简介 Fiddler不但能截获各种浏览器发出的 HTTP 请求,也可以截获各种智能手机发出的HTTP/ HTTPS 请求。 Fiddler 能捕获Android 和 Windows Phone 等设备发出的 HTTP/HTTPS 请求。同理也可以截获iOS设备发出的请求,比如 iPhone、iPad 和 MacBook 等苹…...
