数模方法论-整数规划
一、基本概念
非线性规划的应用包括工程设计、资源分配、经济模型等。在求解过程中,由于非线性特性,常用的方法有梯度法、牛顿法、启发式算法等。求解非线性规划问题时,解的存在性和唯一性通常较难保证,且可能存在多个局部最优解。
非线性规划是数学建模中处理优化问题的一种方法,尤其在目标函数或约束条件为非线性时。它的基本形式可以表示为:

二、实际应用
1、投资决策问题



三、程序代码求解方法
1、例题一

MATLAB求解
clc,clear
x0=[150 85 150 145 130 0];
y0=[140 85 155 50 150 0];
q=[243 236 220.5 159 230 52];
xy0=[x0; y0];
d0=dist(xy0); %求矩阵各个列向量之间的距离
d0(find(d0==0))=inf;
a0=asind(8./d0) %以度为单位的反函数
xy1=x0+i*y0
xy2=exp(i*q*pi/180)
for m=1:6for n=1:6if n~=mb0(m,n)=angle((xy2(n)-xy2(m))/(xy1(m)-xy1(n))); endend
end
b0=b0*180/pi;
dlmwrite('txt1.txt',a0,'delimiter', '\t','newline','PC');
dlmwrite('txt1.txt','~','-append'); %往纯文本文件中写LINGO数据的分割符
dlmwrite('txt1.txt',b0,'delimiter', '\t','newline','PC','-append','roffset', 1)
Python求解
import numpy as np# 初始化数据
x0 = np.array([150, 85, 150, 145, 130, 0])
y0 = np.array([140, 85, 155, 50, 150, 0])
q = np.array([243, 236, 220.5, 159, 230, 52])
xy0 = np.vstack((x0, y0))# 计算距离矩阵
def dist(xy):return np.linalg.norm(xy[:, np.newaxis] - xy[:, np.newaxis].T, axis=0)d0 = dist(xy0)
d0[d0 == 0] = np.inf # 将距离为0的值设为无穷大a0 = np.degrees(np.arcsin(8.0 / d0)) # 以度为单位的反正弦# 复数表示
xy1 = x0 + 1j * y0
xy2 = np.exp(1j * np.radians(q))# 计算角度矩阵
b0 = np.zeros((6, 6))
for m in range(6):for n in range(6):if n != m:b0[m, n] = np.angle((xy2[n] - xy2[m]) / (xy1[m] - xy1[n]))b0 = np.degrees(b0)# 写入文件
np.savetxt('txt1.txt', a0, delimiter='\t', newline='\n')
with open('txt1.txt', 'a') as f:f.write('~\n') # 写入分隔符np.savetxt(f, b0, delimiter='\t', newline='\n', fmt='%f', header='', comments='', footer='', encoding='utf-8')
2、例题二

MATLAB求解
function [g,h]=fun2(x);
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束function f=fun1(x);
f=sum(x.^2)+8;[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')Python求解
import numpy as np
from scipy.optimize import minimize# 非线性不等式约束
def constraints_inequality(x):return np.array([-x[0]**2 + x[1] - x[2]**2,x[0] + x[1]**2 + x[2]**3 - 20])# 非线性等式约束
def constraints_equality(x):return np.array([-x[0] - x[1]**2 + 2,x[1] + 2*x[2]**2 - 3])# 目标函数
def objective(x):return np.sum(x**2) + 8# 初始猜测
x0 = np.random.rand(3)# 定义约束
cons = [{'type': 'ineq', 'fun': constraints_inequality},{'type': 'eq', 'fun': constraints_equality}]# 优化
result = minimize(objective, x0, constraints=cons, bounds=[(0, None)]*3)# 输出结果
print("Optimal solution:", result.x)
print("Objective function value:", result.fun)
![]()
相关文章:

数模方法论-整数规划
一、基本概念 非线性规划的应用包括工程设计、资源分配、经济模型等。在求解过程中,由于非线性特性,常用的方法有梯度法、牛顿法、启发式算法等。求解非线性规划问题时,解的存在性和唯一性通常较难保证,且可能存在多个局部最优解…...

【问题随记】在使用 AuthenticationManager 的时候,出现循环依赖问题 —— `java.lang.StackOverflowError`
问题随记 在使用 AuthenticationManager 的时候,出现循环依赖问题 —— java.lang.StackOverflowError,查资料查了两天半,终于找到原因。 2024-06-16T17:54:19.48708:00 ERROR 20672 --- [nio-8789-exec-1] o.a.c.c.C.[.[.[/].[dispatcherS…...

2024年华为杯-研赛F题论文问题一二讲解+代码分享
X射线脉冲星光子到达时间建模 摘要 脉冲星是一类高速自转的中子星,其自转形成规律性脉冲信号,类似于“宇宙中的灯塔”,因此被认为是极为精确的时钟。X射线脉冲星导航利用脉冲星信号为航天器提供时间和空间参考。通过比较脉冲信号到达航天器…...

代码随想录训练营第34天|dp前置转移
62. 不同路径 class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector<int>(n,1));for(int i1; i<m;i){for(int j1; j<n; j){dp[i][j]dp[i-1][j]dp[i][j-1];}}return dp[m-1][n-1];} }; dp[i][j]:运动至(i,j)的方…...

乐观锁、悲观锁
一、悲观锁 悲观锁 (Pessimistic Locking),具有强烈的独占和排他特性。它指的是对数据被外界修改持保守态度。因此,在整个执行过程中,将处于锁定状态。所以,悲观锁是一种悲观思想,它总认为最坏的情况可能会出现&#x…...
Java客户端SpringDataRedis(RedisTemplate使用)
文章目录 ⛄概述⛄快速入门❄️❄️导入依赖❄️❄️配置文件❄️❄️测试代码 ⛄数据化序列器⛄StringRedisTemplate⛄RedisTemplate的两种序列化实践方案总结 ⛄概述 SpringData是Spring中数据操作的模块,包含对各种数据库的集成,其中对Redis的集成模…...

wsl2桥接网络 ubuntu到弃坑到又跳坑
搜索Hyper-V image.png 如下图进入虚拟交换机管理器 image.png image.png C:\Users\Administrator下存放 ; 这是 WSL 2 的配置文件 [wsl2] processors4 ; 设置 WSL 2 可以使用的最大 CPU 核心数为 4,自行修改 memory4GB …...

WIFI路由器的套杆天线简谈
❝本次推文简单介绍下WIFI路由器的套杆天线。 路由器天线 路由器在这个万物互联的时代,想必大家对其都不陌生。随着科技的发展,常用的路由器上的天线也越来越多,那么问题来了:天线越多,信号越好吗?路由器…...

希尔排序(C语言实现)
目录 1.希尔排序( 缩小增量排序 ) 2.动图 编辑 3.代码实现 预排序实现 子序列排列实现 单趟排序实现 对整组数进行子排序 希尔排序代码 代码测试 时间复杂度分析 希尔排序的特性总结: 1.希尔排序( 缩小增量排序 ) 基本思想: 1.先选定一个…...

LLVM 中的Value、User、Use设计
概述 LLVM是一个强大的编译器基础设施,提供了一套丰富的库,用于构建编译器的前端和后端。在LLVM中,Value、User和Use是几个核心的概念,它们之间有着紧密的关系 Value Value是LLVM中表示所有可计算的值的基类,例如常…...
)
C++智能指针入门教程(C++11)
智能指针 1.定义 C中的智能指针是一种用于自动管理动态分配的内存的模板类,它们通过封装原始指针来提供自动的内存管理功能,从而避免了内存泄漏和悬挂指针等问题。C标准库中提供了几种智能指针类型,其中最常用的是std::unique_ptr、std:…...

常用工具推荐!分享7款AI论文修改软件工具网站
在当今学术研究和写作领域,AI论文修改软件工具已经成为了不可或缺的助手。这些工具不仅能够帮助研究人员提高写作效率,还能确保论文的质量和原创性。以下是七款值得推荐的AI论文修改软件工具网站,其中特别推荐千笔-AIPassPaper。 1. 千笔-AI…...

怎么解除BitLocker对磁盘的加密?
BitLocker是一种Windows操作系统内置的加密功能,用于保护用户的数据安全。它通过对整个磁盘进行加密,防止数据被未经授权的用户访问。BitLocker主要用于保护笔记本电脑和台式机中的重要数据,尤其是在设备丢失或被盗的情况下。怎么解除BitLock…...
群晖使用Docker部署WPS Office并实现异地使用浏览器制作办公文档
文章目录 前言1. 本地环境配置2. 制作本地分享链接3. 制作公网访问链接4. 公网ip地址访问您的分享相册5. 制作固定公网访问链接 前言 想象一下这个场景:如果遇到周末紧急需要改方案,但团队成员都在各自家中,这个时候如果大家能够轻松访问这个…...

Unity3d 以鼠标位置点为中心缩放视角(正交模式下)
思路整理: 缩放前: 缩放后: 记录缩放前鼠标的屏幕坐标 A,计算鼠标位置对应的世界坐标 A_world 缩放完成后,根据当前屏幕下A所对应的世界坐标A1_world 计算A1_world 和 A_world 的偏移量 移动摄像机 代码ÿ…...

Git清除某文件所有历史提交记录
一、软件要求 1.1 软件版本要求 git > 2.22.0python3 > 3.5 1.2 辅助插件 git filter-repo Linux/macOS # Debian/Ubuntu 系统 # 或使用 pip 安装pip install git-filter-repo sudo apt install git-filter-repo Windows pip install git-filter-repo二、操作步骤…...
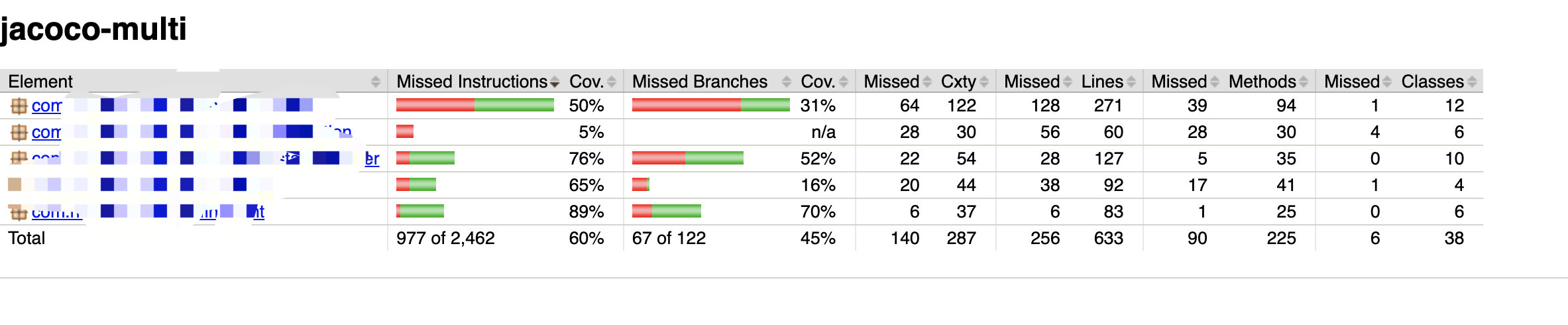
jacoco生成单元测试覆盖率报告
前言 单元测试是日常编写代码中常用的,用于测试业务逻辑的一种方式,单元测试的覆盖率可以用来衡量我们的业务代码经过测试覆盖的比例。 目前市场上开源的单元测试覆盖率的java插件,主要有Emma,Cobertura,Jacoco。具体…...

【CSS Tricks】如何做一个粒子效果的logo
效果展示 代码展示 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>粒子效果Logo</title>…...

如何使用ssm实现基于Javaweb的网上花店系统的设计与实现
TOC ssm653基于Javaweb的网上花店系统的设计与实现jsp 研究背景 自计算机发展以来给人们的生活带来了改变。第一代计算机为1946年美国设计,最开始用于复杂的科学计算,占地面积、开机时间要求都非常高,经过数十几的改变计算机技术才发展到今…...

Elastic 的 OpenTelemetry PHP 发行版简介
作者:Pawel Filipczak 宣布 OpenTelemetry PHP 的 Elastic 发行版的第一个 alpha 版本。在本篇博文中了解使用 OpenTelemetry 来检测 PHP 应用程序是多么简单。 我们很高兴推出 OpenTelemetry PHP 的 Elastic Distribution 的第一个 alpha 版本。在这篇文章中&…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
