位图与布隆过滤器
引例
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
思路1:排序+二分查找
思路2:哈希或红黑树
因为40亿个整数要占用16GB
102410241024Byte 约等于10亿Byte=1GB
40亿*4Byte = 16GB
16G太大放不进内存,就算我们用归并排序对文件排序,也无法对文件使用二分查找,如果一段一段的放进内存里面查找的话,还不如在读取的时候就直接把他那个数挨个查找,放在内存,所以用哈希桶和红黑存储就更加不可能了,毕竟红黑树和哈希桶存储还有导致其他的内存开销。
位图
位图就是用数据中的一个位来标识,然后用哈希的直接定址法存储那一个标识bit位来表示某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
逻辑结构图:
 问:如何确定我要存储的x值应该存储到哪一个位置?
问:如何确定我要存储的x值应该存储到哪一个位置?
x/8=x存储在那一个char里面
x%8= x存储在char的那一个位里面
问:如何在第一个char中的第5个字节置为1?
对0x01左移动5位(设为y),然后再对第一个char(设为x),x|=y,因为0|或任何数都是该数本身,而1|任何数都是1
注意,这里的为什么是左移而不是右移,要清楚左右移不是指移动的方向,而是指右移一向低地址移动,左移-向高地址移动
问:如何在第一个char中的第5个字节置为0?
对0x01左移动5位(设为y),在对y取反就会得到 1110 1111, x&=y,因为1&任何数都是该数本身,而0&任何数都是0
位图的作用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
代码实现:
#pragma once
#include <vector>
using namespace std;template<size_t N>
class bitset
{
public:bitset(){_bits.resize(N / 8 + 1, 0);}//置1void set(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] |= (0x01 << j);//为什么是左移动}//置零void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] &= ~(0x01 << j);}// 查值bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (0x01 << j);}private:vector<char> _bits;
};
int main()
{bitset<-1> bitset;return 0;
}
注意这里这个bitset使用了一个非类型的模版参数来传入一个N用来表述,用于在开空间的时候要开多少多大?
非类型模板参数
模板参数分类类型形参与非类型形参。
类型形参即:出现在模板参数列表中,跟在class或者typename之类的参数类型名称。
非类型形参,就是用一个常量作为类(函数)模板的一个参数,在类(函数)模板中可将该参数当成常量来使用。
引例的解决方案
把40亿存到位图中,再用位图的test去查那个无符号整数到底有没有在位图里面
位图的题目:
1. 给定100亿个整数,设计算法找到只出现一次的整数?
解答:用两个位图来标识出现的状态, 00表示一次都没有出现,01表示出现一次,如果在01状态之后再出现的话就是多次出现
2. 1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
解答:同样用两个位图来标识出现的状态00一次都没有出现 01出现一次 10出现两次 11出现两次以上。
代码实现
#pragma once
#include "bitset.h"template<size_t N>
class TwoBitset
{
public:// 给定100亿个整数,设计算法找到只出现一次的整数?bool Test_OneTime(size_t x) const{if (bit1.test(x) && !bit2.test(x)){return true;}return false;}// 1个文件有100亿个int,1G内存,// 设计算法找到出现次数不超过2次的所有整数bool Test_NoMoreThanTwoTime(size_t x) const{if (bit1.test(x) && bit2.test(x)){return false;}return true;}void set(size_t x){if (!bit1.test(x) && !bit2.test(x)){bit1.set(x);}else if (bit1.test(x) && !bit2.test(x)){bit1.reset(x);bit2.set(x);}else if (!bit1.test(x) && bit2.test(x)){bit1.set(x);}}
private:bitset<N> bit1;bitset<N> bit2;
};
3. 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
解答:用两个位图来存储两个文件,然后再对两个位图进行 &预算,得出的第三个位图就是交集
代码实现
//给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
void intersection()
{int a1[] = { 100,21,21,32,121,123,123,31,32,12,41,213,231,413312,312,213,122 };int a2[] = { -1,-1,100,21,21,21,32,32,121,123,123,31,32,1,12,4321,24,12,412, };bitset<-1> bit1;bitset<-1> bit2;for (auto val : a1){bit1.set(val);}for (auto val : a2){bit2.set(val);}for (size_t i = 0; i < -1; i++){if (bit1.test(i) && bit2.test(i)){cout << i << endl;}}
}
位图的缺点
只能映射整形,其他类型如:浮点数、string等等不能存储映射
布隆过滤器
布隆过滤器是由布隆在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你“某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
布隆过滤器就是用位图+多个哈希函数映射来确定字符串在不在的一个key模型,但是布隆过滤器确定一个字符串不在是准确的,在是不准确的,如下图:
我们存放不同名字的时候,会映射三个位置,如果我搜寻这字符串的时候少于三个位置就是不在的,为什么呢?因为我们是映射是通过三个函数去映射三个位置,如果只有二个位置,那么就证明我并没有存进来,这那个位置只不过是存放其他值的时候刚好冲突到该字符串映射的位置而已,而为什么说在是不准的呢?是因为这三个映射位置也有可能是其他值冲突导致碰巧映射到而已。

White是没有映射存放的,但是碰巧他的映射位置被其他字符串冲突了
布隆过滤器实现代码
struct BKDRHash
{size_t operator()(const string& s){size_t hash = 0;for (auto ch : s){hash += ch;hash *= 31;}return hash;}
};struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){size_t ch = s[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};// N最多会插入key数据的个数
template<size_t N,
class K = string,
class Hash1 = BKDRHash,
class Hash2 = APHash,
class Hash3 = DJBHash>
class BloomFilter
{
public:void set(const K& key){size_t len = N*_X;size_t hash1 = Hash1()(key) % len;_bs.set(hash1);size_t hash2 = Hash2()(key) % len;_bs.set(hash2);size_t hash3 = Hash3()(key) % len;_bs.set(hash3);//cout << hash1 << " " << hash2 << " " << hash3 << " " << endl << endl;}bool test(const K& key){size_t len = N*_X;size_t hash1 = Hash1()(key) % len;if (!_bs.test(hash1)){return false;}size_t hash2 = Hash2()(key) % len;if (!_bs.test(hash2)){return false;}size_t hash3 = Hash3()(key) % len;if (!_bs.test(hash3)){return false;}// 在 不准确的,存在误判// 不在 准确的return true;}
private:static const size_t _X = 6;bitset<N*_X> _bs;
};
布隆过滤器的场景
能容忍误判的场景。比如:注册时,快速判断昵称是否使用过,假设现在要实现注册表单去判断有没有人用过昵称,就可以用到布隆过滤器,因为布隆过滤器对于不在这个结果是准确的。所以可以把昵称存放在布隆过滤器中快速过滤
哈希切分
题目1:给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
首先,估算一下文件大小,100亿个query大概需要占用多少空间? 假设单个query,平均50byte,100亿个query是5000亿byte大概估算占用500G
用哈希函数把文件映射成小文件

为什么哈希切分只需要找A、B中对应i号的文件即可?
因为在哈希切分的时候,query字符串经过哈希函数的切分,会把冲突的字符串放在同一个桶里,只需要桶对桶之间进行交集计算即可
问题:因为不是平均切分,可能会出现冲突多,每个Ai,Bi小文件过大。…假设两个都是4-5G
所以要分类处理,
直接使用一个unordered set/set,依次读取文件query,插入set中
1、如果读取整个小文件query,都可以成功插入set,那么说明单个文件有大量重复的query
2、如果读取整个小文件query,插入过程中抛异常,则是单个文件有大量不同的query,换其他哈希函数,再次分割,再求交集。说明:set插入key,如果已经有了,返回false;如果没有内存,会抛bad alloc异常,剩下的都会成功。
相关文章:

位图与布隆过滤器
引例 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。 思路1:排序二分查找 思路2:哈希或红黑树 因为40亿个整数要占用16GB 102410241024Byte 约等于10亿Byte1GB 40亿*4Byte 16G…...

【题解】—— LeetCode一周小结38
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结37 16.公交站间的距离 题目链接:1184. 公交站间的距…...
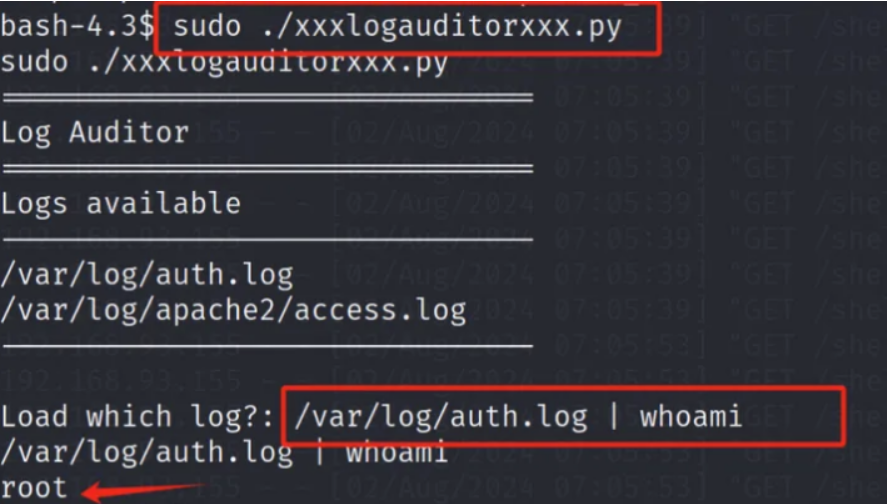
EvilScience靶机详解
主机发现 arp-scan -l 得到靶机ip 192.168.229.152 端口扫描 nmap -sV -A -T4 192.168.1.20 这段代码使用 nmap 命令来扫描目标主机 192.168.1.20,并执行以下操作:-sV:探测开放的端口,以确定服务/版本信息。-A:启…...

算法练习题24——leetcode3296移山所需的最小秒数(二分模拟)
【题目描述】 【代码示例(java)】 class Solution {// 计算让工人们将山的高度降到0所需的最少时间public long minNumberOfSeconds(int mountainHeight, int[] workerTimes) {long left 0; // 最少时间初始为0long right 0; // 最大时间初始化为0// …...

excel 单元格一直显示年月日
excel 单元格一直显示年月日,在单元格上右键选择单元格格式,选择日期时单元格会显示成日期格式...

【线程】线程的控制
本文重点:理解线程控制的接口 前言 内核中是没有很明确线程的概念的,只有轻量级进程的概念,不会提供直接给我们线程的系统调用,而会给我们提供轻量级进程的系统调用。我们用户是需要线程的接口的,在应用层࿰…...

掌握 Spring:从新手到高手的常见问题汇总
一提起Spring,总感觉有太多知识,无法详尽,有些基础理解就先不说了,相信大家都已经用过Spring了 下面简单针对常见Spring面试题做些回答 核心特性 IOC容器spring事件资源管理国际化校验数据绑定类型转换spirng表达式面向切面编程……...

机器学习——Bagging
Bagging: 方法:集成n个base learner模型,每个模型都对原始数据集进行有放回的随机采样获得随机数据集,然后并行训练。 回归问题:n个base模型进行预测,将得到的预测值取平均得到最终结果。 分类问题…...

日志体系结构与框架:历史、实现与如何在 Spring Cloud 中使用日志体系
文章目录 1. 引言2. 日志体系结构3. 日志框架的发展历程日志框架特点对比 4. 日志记录器的使用与管理使用 SLF4J 和 Logback 的日志记录示例 5. Spring Cloud 中的日志使用5.1 日志框架集成5.2 分布式追踪:Spring Cloud Sleuth 和 Zipkin添加 Sleuth 和 Zipkin 依赖…...

图文深入理解SQL语句的执行过程
List item 本文将深入介绍SQL语句的执行过程。 一.在RDBMS(关系型DB)中,看似很简单的一条已写入DB内存的SQL语句执行过程却非常复杂,也就是说,你执行了一条诸如select count(*) where id 001 from table_name的非常简…...

ubuntu安装StarQuant
安装boost 下面展示一些 内联代码片。 sudo apt install libboost-all-dev -y安装libmongoc-1.0 链接: link // An highlighted block sudo apt install libmongoc-1.0-0 sudo apt install libbson-1.0 sudo apt install cmake libssl-dev libsasl2-dev编译源码 $ git clone…...
)
学习篇 | Jupyter 使用(notebook hub)
1. JupyterHub 1.1 快速尝试 jupyterhub -f/path/jupyter_config.py --no-ssl1.2 长期后台运行 bash -c "nohup jupyterhub -f/path/jupyter_config.py --no-ssl" > ~/jupyterhub.log 2>&1 &1.3 帮助 jupyterhub --help2. Jupyter Notebook 2.1 快…...
-虚拟内存swap交换分区扩展)
【裸机装机系列】8.kali(ubuntu)-虚拟内存swap交换分区扩展
推荐阅读: 1.kali(ubuntu)-为什么弃用ubuntu,而选择基于debian的kali操作系统 linux swap交换分区,相当于win系统虚拟内存的概念。当linux系统的物理内存不够用的时候,就需要将物理内存中的一部分空间释放出来,以供当前…...

异步请求的方法以及原理
异步请求是指在发送请求后,不会阻塞程序的执行,而是继续执行后续的代码,等待请求返回后再执行相应的回调函数。常见的异步请求方法包括使用XMLHttpRequest对象(XHR)和fetch API。 异步请求的方法 1. XMLHttpRequest (X…...

SpringCloud入门(六)Nacos注册中心(下)
一、Nacos环境隔离 Nacos提供了namespace来实现环境隔离功能。 nacos中可以有多个namespace。namespace下可以有group、service等。不同namespace之间相互隔离,例如不同namespace的服务互相不可见。 使用Nacos Namespace 环境隔离 步骤: 1.在Nacos控制…...

【RDMA】mlxlink检查和调试连接状态及相关问题--驱动工具
简介 mlxlink工具用于检查和调试连接状态及相关问题。该工具可以用于不同的链路和电缆(包括被动、电动、收发器和背板)。 属于mft工具套件的一个工具,固件工具 Firmware Tools (MFT):https://blog.csdn.net/bandaoyu/article/details/14242…...

QT For Android开发-打开PPT文件
一、前言 需求: Qt开发Android程序过程中,点击按钮就打开一个PPT文件。 Qt在Windows上要打开PPT文件或者其他文件很容易。可以使用QDesktopServices打开文件,非常方便。QDesktopServices提供了静态接口调用系统级别的功能。 这里用的QDesk…...
SpringBoot教程(三十) | SpringBoot集成Shiro权限框架
SpringBoot教程(三十) | SpringBoot集成Shiro权限框架 一、 什么是Shiro二、Shiro 组件核心组件其他组件 三、流程说明shiro的运行流程 四、SpringBoot 集成 Shiro (shiro-spring-boot-web-starter方式)1. 添加 Shiro 相关 maven2…...

[ffmpeg] 视频格式转换
本文主要梳理 ffmpeg 中的视频格式转换。由于上屏的数据是 rgba,编码使用的是 yuv数据,所以经常会使用到视频格式的转换。 除了使用 ffmpeg进行转换,还可以通过 libyuv 和 directX 写 shader 进行转换。 之前看到文章说 libyuv 之前是 ffmpeg…...
 git-repo https证书认证问题)
git-repo系列教程(3) git-repo https证书认证问题
文章目录 问题描述解决步骤1.下载证书2.测试证书是否正常3.设置环境变量 总结 问题描述 在使用git repo 同步仓库时,发现不能同步,出现如下提示错误: % Total % Received % Xferd Average Speed Time Time Time CurrentDload Upload Total Spent Left …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
