论文阅读:A Generalization of Transformer Networks to Graphs
论文阅读:A Generalization of Transformer Networks to Graphs
- 论文地址
- 1 摘要
- 2 贡献
- Graph Transformer
- On Graph Sparsity(图稀疏)
- On Positional Encodings(位置编码)
- 3 Graph Transformer Architecture(架构)
- 模型框架
- input(输入)
- Graph Transformer Layer
- Graph Transformer Layer with edge features(带边特征)
- 基于任务的 MLP 层
- 4 实验
论文地址
论文:https://arxiv.org/pdf/2012.09699.pdf
代码:https://github.com/graphdeeplearning/graphtransformer
1 摘要
作者提出了一种适用于任何图的GraphTransformer。原始的transformer在基于单词的全连接图上用于NLP,它有如下缺点:
- 这种结构不能很好利用图的连通归纳偏置(graph connectivity inductive bias)
- 当图的拓扑结构很重要且尚未编码到节点特征时,表现很差
作者提出的GraphTransformer,有4个优势:
- 注意力机制是图中每个节点的邻域连通性的函数
- positional encoding用拉普拉斯特征向量表示
- Batch Normalization代替Layer Normalization,优点:训练更快,泛化性能更好
- 该架构扩展到边特征表示,这对于某些任务可能至关重要,例如化学(键类型)或链接预测(知识图谱中的实体关系)
2 贡献
- 提出了一种将 transformer 网络推广到任意结构的同构图,即 Graph Transformer,以及具有边缘特征的 GraphTransformer 的扩展版本,允许使用显式域信息作为边缘特征。
- 方法包括一种使用拉普拉斯特征向量为图数据集融合节点位置特征的优雅方法。与文献的比较表明,拉普拉斯特征向量比任何现有的方法都更适合编码任意同构图的节点位置信息
- 实验表明,所提出的模型超过了baseline的各向同性和各向异性 GNN
Graph Transformer
On Graph Sparsity(图稀疏)
在NLP的transformer中,用全连接图去处理一个句的原因:
- 很难在句子中的单词之间找到有意义的稀疏交互或联系。例如:句子中的单词对另一个单词的依赖性可能因上下文、用户视角而异
- NLP的transformer的nodes数量比较少(几十个,几百个),便于计算。
对于实际的图形数据集,图形可能有任意的连接结构,nodes的数量高达数百万或数十亿,使得不可能为此类数据集提供完全连接的图形,因此需要Graph Transformer来让nodes处理邻居信息。
On Positional Encodings(位置编码)
在 NLP 中,基于 transformer 的模型为每个单词提供位置编码。确保每个单词的唯一表示并确保最终保留距离信息
对于图形,唯一节点位置的设计具有挑战性,因此大多数在图数据集上训练的 GNN 学习的是不随节点位置变化的结构化节点信息,这就是为什么GAT是局部attention,而不是全局attention。
现在的目标是学习结构和位置的特征,Dwivedi et al. (2020)利用现有的图结构预先计算拉普拉斯特征向量,并将它们作为节点的位置信息。
- 拉普拉斯 PE 能更好地帮助编码距离感知信息(即,附近的节点具有相似的位置特征,而较远的节点具有不同的位置特征)
因此使用拉普拉斯特征向量作为 Graph Transformer 中的 PE。特征向量通过图拉普拉斯矩阵的分解来定义:
Δ = I − D − 1 / 2 A D − 1 / 2 = U T Λ U , ( 1 ) \Delta=\mathrm{I}-D^{-1/2}AD^{-1/2}=U^T\Lambda U,\quad(1) Δ=I−D−1/2AD−1/2=UTΛU,(1)
- A A A是 n × n n\times n n×n邻接矩阵, D D D是度矩阵
- Λ \Lambda Λ和 U U U分别对应特征值和特征向量
- 使用节点的 k个最小的非平凡特征向量作为其位置编码,对于节点 i i i,用 λ i \lambda_{i} λi表示
3 Graph Transformer Architecture(架构)
模型框架

input(输入)
首先准备要输入Graph Transformer Layer的input node 和 edge embeddings。
在图 G \mathcal{G} G中,对于任意一个节点 i i i的节点特征 α i ∈ R d n × 1 \alpha_{i} \in \mathbb{R}^{d_{n}\times1} αi∈Rdn×1以及节点 i i i和节点 j j j之间的边特征 β i j ∈ R d e × 1 \beta_{ij}\in\mathbb{R}^{d_{e}\times1} βij∈Rde×1, α i \alpha_{i} αi和 β i j \beta_{ij} βij通过一个线性映射,从而嵌入到 d d d维的隐藏特征(hidden features) h i 0 h_i^0 hi0和 e i j 0 e_{ij}^0 eij0中,公式如下:
h ^ i 0 = A 0 α i + a 0 ; e i j 0 = B 0 β i j + b 0 , ( 2 ) \hat{h}_i^0=A^0\alpha_i+a^0 ; e_{ij}^0=B^0\beta_{ij}+b^0,\quad(2) h^i0=A0αi+a0;eij0=B0βij+b0,(2)
-
其中 A 0 ∈ R d × d n , B 0 ∈ R d × d e A^0\in\mathbb{R}^{d\times d_n},B^0\in\mathbb{R}^{d\times d_e} A0∈Rd×dn,B0∈Rd×de,以 A 0 A^0 A0为例,其每一列是每个节点的节点特征(总共 d n d_n dn个结点),维度为 d d d,而 α i \alpha_{i} αi一个其他元素都为0,对应节点位置的元素为1的向量
-
a 0 , b 0 ∈ R d a^0,b^0\in\mathbb{R}^d a0,b0∈Rd是线性映射层的参数
然后通过线性映射嵌入维度为 k k k的预计算节点位置编码并将其添加到节点特征 h ^ i 0 \hat{h}_i^0 h^i0中。
λ i 0 = C 0 λ i + c 0 ; h i 0 = h ^ i 0 + λ i 0 , ( 3 ) \lambda_i^0=C^0\lambda_i+c^0 ; h_i^0=\hat{h}_i^0+\lambda_i^0,\quad(3) λi0=C0λi+c0;hi0=h^i0+λi0,(3)
- 其中 C 0 ∈ R d × k , c 0 ∈ R d C^0\in\mathbb{R}^{d\times k},c^0\in\mathbb{R}^d C0∈Rd×k,c0∈Rd,其作用是将位置编码转化为维度为 d d d的向量
Graph Transformer Layer
现在定义第 l l l层的节点更新方程:
h ^ i ℓ + 1 = O h ℓ ∣ ∣ k = 1 H ( ∑ j ∈ N i w i j k , ℓ V k , ℓ h j ℓ ) , ( 4 ) \hat{h}_{i}^{\ell+1}=O_{h}^{\ell}\mathcal{\left|\right|}_{k=1}^{H}\Big(\sum_{j\in\mathcal{N}_{i}}w_{ij}^{k,\ell}V^{k,\ell}h_{j}^{\ell}\Big),\quad(4) h^iℓ+1=Ohℓ∣∣k=1H(j∈Ni∑wijk,ℓVk,ℓhjℓ),(4)
w h e r e , w i j k , ℓ = s o f t m a x j ( Q k , ℓ h i ℓ ⋅ K k , ℓ h j ℓ d k ) , ( 5 ) \mathrm{where,~}w_{ij}^{k,\ell}=\mathrm{softmax}_{j}\Big(\frac{Q^{k,\ell}h_{i}^{\ell} \cdot K^{k,\ell}h_{j}^{\ell}}{\sqrt{d_{k}}}\Big),\quad(5) where, wijk,ℓ=softmaxj(dkQk,ℓhiℓ⋅Kk,ℓhjℓ),(5)
- Q k , ℓ , K k , ℓ , V k , ℓ ∈ R d k × d , O h ℓ ∈ R d × d Q^{k,\ell},K^{k,\ell},V^{k,\ell}\in\mathbb{R}^{d_{k}\times d},O_{h}^{\ell}\in\mathbb{R}^{d\times d} Qk,ℓ,Kk,ℓ,Vk,ℓ∈Rdk×d,Ohℓ∈Rd×d
- k = 1 k=1 k=1到 H H H代表注意头的数量
- ∣ ∣ \mathcal{\left|\right|} ∣∣表示串联(concatenation)
这里详细讲一下式子(5), Q k , ℓ h i ℓ Q^{k,\ell}h_{i}^{\ell} Qk,ℓhiℓ相当于 h i ℓ h_{i}^{\ell} hiℓ的查询向量, K k , ℓ h j ℓ K^{k,\ell}h_{j}^{\ell} Kk,ℓhjℓ是 h j ℓ h_{j}^{\ell} hjℓ的键向量(相当于查询的答案)
- 比如,查询向量在问:“我前面有形容词吗”,键向量回答:“有的”。假设二者向量点积值越大,则说明了它们越匹配,则说明越相关
- 除以 d k \sqrt{d_{k}} dk是为了数据的稳定性
接着将结果 h ^ i ℓ + 1 \hat{h}_{i}^{\ell+1} h^iℓ+1按照框架图所示依次经过残差连接和LN、Feed Forward Network (FFN)、残差连接和LN,公式如下:
h ^ ^ i ℓ + 1 = Norm ( h i ℓ + h ^ i ℓ + 1 ) , ( 6 ) h ^ ^ ^ ℓ + 1 = W 2 ℓ ReLU ( W 1 ℓ h ^ ^ i ℓ + 1 ) , ( 7 ) h i ℓ + 1 = Norm ( h ^ ^ i ℓ + 1 + h ^ ^ ^ i ℓ + 1 ) , ( 8 ) \hat{\hat{h}}_i^{\ell+1}\quad=\quad\text{Norm}\Big(h_i^\ell+\hat{h}_i^{\ell+1}\Big),\quad(6) \newline \begin{array}{lcl}\hat{\hat{\hat{h}}}^{\ell+1}&=&W_2^\ell\text{ReLU}(W_1^\ell\hat{\hat{h}}_i^{\ell+1}),&(7)\end{array} \newline \begin{array}{rcl}h_i^{\ell+1}&=&\text{Norm}\Big(\hat{\hat{h}}_i^{\ell+1}+\hat{\hat{\hat{h}}}_i^{\ell+1}\Big),&\quad(8)\end{array} h^^iℓ+1=Norm(hiℓ+h^iℓ+1),(6)h^^^ℓ+1=W2ℓReLU(W1ℓh^^iℓ+1),(7)hiℓ+1=Norm(h^^iℓ+1+h^^^iℓ+1),(8)
- W 1 ℓ , ∈ R 2 d × d , W 2 ℓ , ∈ R d × 2 d , h ^ ^ i ℓ + 1 , h ^ ^ ^ i ℓ + 1 W_{1}^{\ell},\in \mathbb{R}^{2d\times d}, W_{2}^{\ell},\in \mathbb{R}^{d\times2d}, \hat{\hat{h}}_{i}^{\ell+1}, \hat{\hat{\hat{h}}}_{i}^{\ell+1} W1ℓ,∈R2d×d,W2ℓ,∈Rd×2d,h^^iℓ+1,h^^^iℓ+1 都是中间变量
- Norm可以是LayerNorm或者BatchNorm
Graph Transformer Layer with edge features(带边特征)
接下来介绍的是上图第二个模型,根据公式(5),将此分数视为边<i,j>的隐式信息,紧接着使用公式(12)为边<i,j>注入可用的边信息,如下:
h ^ i ℓ + 1 = O h ℓ ∣ ∣ k = 1 H ( ∑ j ∈ N i w i j k , ℓ V k , ℓ h j ℓ ) , (9) e ^ i j ℓ + 1 = O e ℓ ∣ ∣ k = 1 H ( w ^ i j k , ℓ ) , w h e r e , (10) w i j k , ℓ = s o f t m a x j ( w ^ i j k , ℓ ) , (11) w ^ i j k , ℓ = ( Q k , ℓ h i ℓ ⋅ K k , ℓ h j ℓ d k ) ⋅ E k , ℓ e i j ℓ , (12) \begin{aligned}&\hat{h}_{i}^{\ell+1}&&=\quad O_{h}^{\ell}\mathcal{\left|\right|}_{k=1}^{H}\Big(\sum_{j\in\mathcal{N}_{i}}w_{ij}^{k,\ell}V^{k,\ell}h_{j}^{\ell}\Big),&&\text{(9)}\\&\hat{e}_{ij}^{\ell+1}&&=\quad O_{e}^{\ell}\mathcal{\left|\right|}_{k=1}^{H}\Big(\hat{w}_{ij}^{k,\ell}\Big), \mathrm{where},&&\text{(10)}\\&w_{ij}^{k,\ell}&&=\quad\mathrm{softmax}_{j}(\hat{w}_{ij}^{k,\ell}),&&\text{(11)}\\&\hat{w}_{ij}^{k,\ell}&&=\quad\left(\frac{Q^{k,\ell}h_{i}^{\ell}\cdot K^{k,\ell}h_{j}^{\ell}}{\sqrt{d_{k}}}\right) \cdot E^{k,\ell}e_{ij}^{\ell},&&\text{(12)}\end{aligned} h^iℓ+1e^ijℓ+1wijk,ℓw^ijk,ℓ=Ohℓ∣∣k=1H(j∈Ni∑wijk,ℓVk,ℓhjℓ),=Oeℓ∣∣k=1H(w^ijk,ℓ),where,=softmaxj(w^ijk,ℓ),=(dkQk,ℓhiℓ⋅Kk,ℓhjℓ)⋅Ek,ℓeijℓ,(9)(10)(11)(12)
- Q k , ℓ , K k , ℓ , V k , ℓ , E k , ℓ ∈ R d k × d , O h ℓ , O e ℓ ∈ R d × d Q^{k,\ell},K^{k,\ell},V^{k,\ell},E^{k,\ell} \in \mathbb{R}^{d_{k}\times d}, O_{h}^{\ell},O_{e}^{\ell} \in \mathbb{R}^{d\times d} Qk,ℓ,Kk,ℓ,Vk,ℓ,Ek,ℓ∈Rdk×d,Ohℓ,Oeℓ∈Rd×d
- 这里的公式,矩阵运算过程中总感觉维度不对应,后期再看这个问题
紧接着,经历相同的过程,如下:
对于节点:
h ^ ^ i ℓ + 1 = N o r m ( h i ℓ + h ^ i ℓ + 1 ) , (13) h ^ ^ ^ i ℓ + 1 = W h , 2 ℓ R e L U ( W h , 1 ℓ h ^ ^ i ℓ + 1 ) , (14) h i ℓ + 1 = N o r m ( h ^ ^ i ℓ + 1 + h ^ ^ ^ i ℓ + 1 ) , (15) \begin{aligned} &\hat{\hat{h}}_{i}^{\ell+1}&& =\quad\mathrm{Norm}\Big(h_{i}^{\ell}+\hat{h}_{i}^{\ell+1}\Big), &&&& \text{(13)} \\ &\hat{\hat{\hat{h}}}_{i}^{\ell+1}&& =\quad W_{h,2}^{\ell}\mathrm{ReLU}(W_{h,1}^{\ell}\hat{\hat{h}}_{i}^{\ell+1}), &&&& \text{(14)} \\ &h_{i}^{\ell+1}&& =\quad\mathrm{Norm}\Big(\hat{\hat{h}}_{i}^{\ell+1}+\hat{\hat{\hat{h}}}_{i}^{\ell+1}\Big), &&&& \text{(15)} \end{aligned} h^^iℓ+1h^^^iℓ+1hiℓ+1=Norm(hiℓ+h^iℓ+1),=Wh,2ℓReLU(Wh,1ℓh^^iℓ+1),=Norm(h^^iℓ+1+h^^^iℓ+1),(13)(14)(15)
- W h , 1 ℓ , ∈ R 2 d × d , W h , 2 ℓ , ∈ R d × 2 d W_{h,1}^{\ell},\in \mathbb{R}^{2d\times d}, W_{h,2}^{\ell},\in \mathbb{R}^{d\times2d} Wh,1ℓ,∈R2d×d,Wh,2ℓ,∈Rd×2d
对于边:
e ^ ^ i j ℓ + 1 = N o r m ( e i j ℓ + e ^ i j ℓ + 1 ) , ( 16 ) e ^ ^ ^ i j ℓ + 1 = W e , 2 ℓ R e L U ( W e , 1 ℓ e ^ ^ i j ℓ + 1 ) , ( 17 ) e i j ℓ + 1 = N o r m ( e ^ ^ i j ℓ + 1 + e ^ ^ ^ i j ℓ + 1 ) , ( 18 ) \hat{\hat{e}}_{ij}^{\ell+1}=\quad\mathrm{Norm}\Big(e_{ij}^{\ell}+\hat{e}_{ij}^{\ell+1}\Big),(16)\\\hat{\hat{\hat{e}}}_{ij}^{\ell+1}=\quad W_{e,2}^{\ell}\mathrm{ReLU}(W_{e,1}^{\ell}\hat{\hat{e}}_{ij}^{\ell+1}),(17)\\e_{ij}^{\ell+1}=\quad\mathrm{Norm}\Big(\hat{\hat{e}}_{ij}^{\ell+1}+\hat{\hat{\hat{e}}}_{ij}^{\ell+1}\Big),(18) e^^ijℓ+1=Norm(eijℓ+e^ijℓ+1),(16)e^^^ijℓ+1=We,2ℓReLU(We,1ℓe^^ijℓ+1),(17)eijℓ+1=Norm(e^^ijℓ+1+e^^^ijℓ+1),(18)
- W e , 1 ℓ , ∈ R 2 d × d , W e , 2 ℓ , ∈ R d × 2 d W_{e,1}^{\ell},\in \mathbb{R}^{2d\times d},W_{e,2}^{\ell},\in \mathbb{R}^{d\times2d} We,1ℓ,∈R2d×d,We,2ℓ,∈Rd×2d
基于任务的 MLP 层
在 Graph Transformer 最后一层获得的节点表示被传递到基于任务的 MLP 网络,用于计算与任务相关的输出,然后将其馈送到损失函数以训练模型的参数
4 实验
为了评估提出的模型的性能,在ZINC,PATTERN,CLUSTER这三个数据集实验。
- ZINC, Graph Regression:分子数据集,node代表分子,edge代表分子之间的键。键之间有丰富的特征信息,所以用第二个模型。
- PATTERN,Node Classification:任务是把nodes分成两个communities,没有明确的edge信息,所以用第一个模型。
- CLUSTER, Node Classification:任务是为每个node分配cluster,一共有6个cluster,用第一个模型。
模型的配置:使用PyTorch,DGL。一共有10层Graph Transformer layers,每层有8个attention head和随机隐藏单元,学习率递减策略,当学习率达到 1 0 − 6 10^{-6} 10−6就停止训练。使用 4 种不同的种子进行每个实验,并报告 4 次运行的平均值和平均性能测量值。
表1如下:
- GraphTransformer (GT) 在所有数据集上的结果。 ZINC 的性能测量是 MAE,PATTERN 和 CLUSTER的性能测量是 Acc。 结果(除了 ZINC 之外,所有结果都越高越好)是使用 4 种不同种子进行 4 次运行的平均值。
- 粗体:每个数据集表现最佳的模型。
- 使用给定的图(稀疏图)和(完整图)执行每个实验,其中完整图在所有节点之间创建完全连接;对于 ZINC 全图,边特征被丢弃。

表2如下所示:
每个数据集上的最佳表现分数(来自表 1)与 GNN baselines的比较

实验结论如下: - 由表1可知,带有PE和BN的模型实验数据更好。
- 由表2可知,提出的模型明显比GCN和GTN要好,但没有GatedGCN好。
- 提出的第二个模型的性能在ZINC上近似于GatedGCN。
相关文章:

论文阅读:A Generalization of Transformer Networks to Graphs
论文阅读:A Generalization of Transformer Networks to Graphs 论文地址1 摘要2 贡献Graph TransformerOn Graph Sparsity(图稀疏)On Positional Encodings(位置编码)3 Graph Transformer Architecture(架…...

中国计量大学《2022年801+2022年819自动控制原理真题》 (完整版)
本文内容,全部选自自动化考研联盟的:《25届中国计量大学801819自控考研资料》的真题篇。后续会持续更新更多学校,更多年份的真题,记得关注哦~ 目录 2022年801真题 2022年819真题 Part1:2022年完整版真题 2022年801…...

创客匠人运营课堂|增强用户的参与度和忠诚度,这一个工具就能实现!
活动投票是通过营销活动来提升用户粘性及平台裂变效果的工具。可以让活动得到更好的传播,平台品牌得到更大的曝光。 使用场景 活动投票是一种互动营销手段,适用于各种活动场景,具有增强用户的参与度和忠诚度,提高活动的透明度和公…...

k8s 微服务 ingress-nginx 金丝雀发布
目录 一 什么是微服务 二 微服务的类型 三 ipvs模式 3.1 ipvs模式配置方式 四 微服务类型详解 4.1 clusterip 4.2 ClusterIP中的特殊模式headless 4.3 nodeport 4.4 loadbalancer 4.5 metalLB 4.6 externalname 五 Ingress-nginx 5.1 ingress-nginx功能 5.2 部署…...

Elasticsearch不停机切换(上云)方案
如何给飞行中的飞机换引擎? 背景 业务背景 略 技术背景 线下集群40个索引左右,总数据量不大,不到100G因为ES承担的业务鉴权业务,所以不能接受停机割接 还有就是ES中数据来自各个业务方,推送的时机不定,也没有完备的重推机制&…...

归纳一下Invoke,beginInvoke,还有InvokeRequire
1.在WinForms中的Invoke和BeginInvoke WinForms是一个单线程的UI框架。在多线程的环境下操作UI控件时。需要使用Invoke和BeginInvoke跨线程调起UI线程 这两的区别如下Invoke:同步调用,当前代码不在UI线程上执行时,会卡住当前线程࿰…...

Prompt最佳实践|指定输出的长度
在OpenAI的官方文档中已经提供了[Prompt Enginerring]的最佳实践,目的就是帮助用户更好的使用ChatGPT 编写优秀的提示词我一共总结了9个分类,本文讲解第6个分类:指定输出长度 提供更多的细节要求模型扮演角色使用分隔符指定任务步骤提供样例…...

离散制造 vs 流程制造:锚定精准制造未来,从装配线到化学反应,实时数据集成在制造业案例中的多维应用
使用 TapData,化繁为简,摆脱手动搭建、维护数据管道的诸多烦扰,轻量替代 OGG, Kettle 等同步工具,以及基于 Kafka 的 ETL 解决方案,「CDC 流处理 数据集成」组合拳,加速仓内数据流转,帮助企业…...

教你一招:在微信小程序中为用户上传的图片添加时间水印
在微信小程序开发过程中,我们常常需要在图片上添加水印,以保护版权或增加个性化元素。本文将为大家介绍如何在微信小程序中为图片添加时间水印,让你的小程序更具特色。 实现步骤: 1. 创建页面结构 在pages目录下创建一个名为upl…...

MySQL --基本查询(上)
文章目录 1.Create1.1单行数据全列插入1.2多行数据指定列插入1.3插入否则更新1.4替换 2.Retrieve2.1 select列2.1.1全列查询2.1.2指定列查询2.1.3查询字段为表达式2.1.4 为查询结果指定别名2.1.5结果去重 2.2where 条件2.2.1英语不及格的同学及英语成绩 ( < 60 )2.2.2语文成…...
(19))
mysql学习教程,从入门到精通,SQL 删除数据(DELETE 语句)(19)
1、SQL 删除数据(DELETE 语句) 在SQL中,TRUNCATE TABLE 语句用于删除表中的所有行,但不删除表本身。这个操作通常比使用 DELETE 语句删除所有行要快,因为它不记录每一行的删除操作到事务日志中,而是直接重…...

RoguelikeGenerator Pro - Procedural Level Generator
这是怎么一回事? Roguelike Generator Pro:简单与力量的结合。使用GameObjects、Tilemaps或自定义解决方案轻松制作3D/2D/2.5D关卡。享受内置功能,如碰撞处理、高度变化、基本控制器和子随机化器,所有这些都由Drunkard Wlak程序生成算法提供支持。 我该如何使用它? 简单:…...
)
反病毒技术和反病毒软件(网络安全小知识)
一、反病毒技术的难点 病毒变异与多态性:病毒开发者不断利用新技术和漏洞,创造出新的病毒变种和多态病毒。这些病毒能够自我变异,从而避开传统的基于特征码的检测方法,使得反病毒软件难以识别和清除。 未知病毒检测:在…...

位图与布隆过滤器
引例 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。 思路1:排序二分查找 思路2:哈希或红黑树 因为40亿个整数要占用16GB 102410241024Byte 约等于10亿Byte1GB 40亿*4Byte 16G…...

【题解】—— LeetCode一周小结38
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结37 16.公交站间的距离 题目链接:1184. 公交站间的距…...
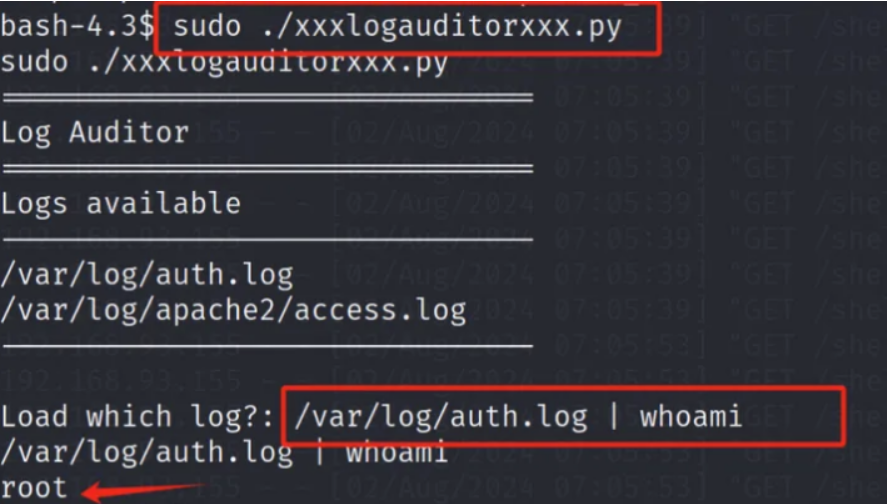
EvilScience靶机详解
主机发现 arp-scan -l 得到靶机ip 192.168.229.152 端口扫描 nmap -sV -A -T4 192.168.1.20 这段代码使用 nmap 命令来扫描目标主机 192.168.1.20,并执行以下操作:-sV:探测开放的端口,以确定服务/版本信息。-A:启…...

算法练习题24——leetcode3296移山所需的最小秒数(二分模拟)
【题目描述】 【代码示例(java)】 class Solution {// 计算让工人们将山的高度降到0所需的最少时间public long minNumberOfSeconds(int mountainHeight, int[] workerTimes) {long left 0; // 最少时间初始为0long right 0; // 最大时间初始化为0// …...

excel 单元格一直显示年月日
excel 单元格一直显示年月日,在单元格上右键选择单元格格式,选择日期时单元格会显示成日期格式...

【线程】线程的控制
本文重点:理解线程控制的接口 前言 内核中是没有很明确线程的概念的,只有轻量级进程的概念,不会提供直接给我们线程的系统调用,而会给我们提供轻量级进程的系统调用。我们用户是需要线程的接口的,在应用层࿰…...

掌握 Spring:从新手到高手的常见问题汇总
一提起Spring,总感觉有太多知识,无法详尽,有些基础理解就先不说了,相信大家都已经用过Spring了 下面简单针对常见Spring面试题做些回答 核心特性 IOC容器spring事件资源管理国际化校验数据绑定类型转换spirng表达式面向切面编程……...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
