【笔记】材料分析测试:晶体学
晶体与晶体结构Crystal and Crystal Structure
1.晶体主要特征
固态物质可以分为晶态和非晶态两大类,分别称为晶体和非晶体。
晶体和非晶体在微观结构上的区别在于是否具有长程有序。
- 晶体(长程有序)
- 非晶(短程有序)
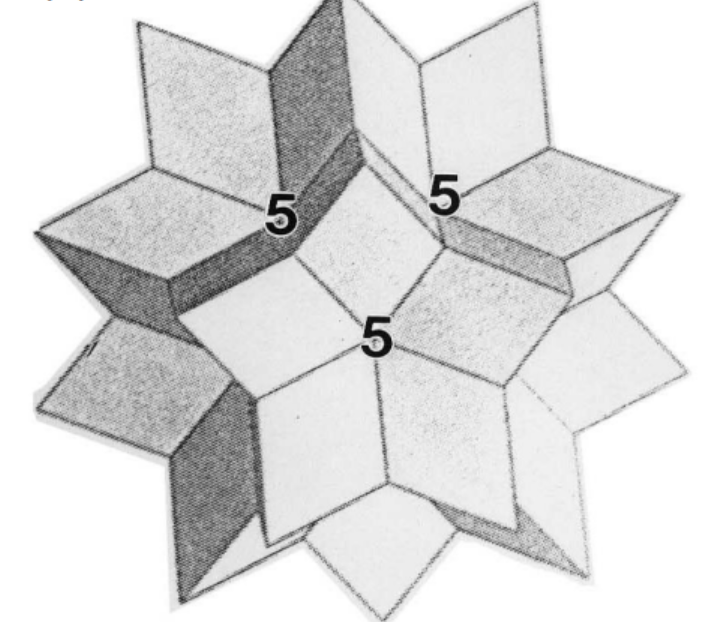
准晶:介于晶体和非晶体之间。准晶体具有与晶体相似的长程有序的原子排列,但是准晶体不具备晶体的平移对称性。因而可以具有晶体所不允许的宏观对称性。普通晶体具有的是二次、三次、四次或六次旋转对称性,但是准晶的布拉格衍射图具有其他的对称性,例如五次对称性或者更高的六次以上对称性。
晶体具有如下基本特征:
晶体的主要特性都源自微观质点的规则排列。
- 对称性:在某些特定方向上各向同性(相同的性质在不同地方有规律地重复出现)
原因:晶体内部质点高度有序排列
反映:方向上旋转对称,微观上平移对称(所以有空间点阵) - 自范性(子限性):晶体自发形成封闭的几何多边形外形。
- 均一性:粒子周期性重复排列,呈现出的各项宏观性质相同。
- 各向异性:晶体内部粒子在不同的方向有不同的排列,所以不同方向展现出不同的性质。
- 稳定性:粒子的规则排列降低晶体内能,处于稳定状态。稳定性体现在晶体具有固定的熔点。
2. 晶体结构
常见晶体很多是多晶,而且内部含有大量取向不同的晶粒和缺陷。
而且晶体内部含有很多规则重复排列的结构单元。
为了研究晶体中质点的排列规律性,将常见晶体视作没有缺陷的理想晶体,又把理想晶体内部周期重复的最小结构单元提取出来,抽象成几何点——阵点。
空间点阵(点阵):阵点在三维空间规则排列的阵列。
晶格(空间格子):用平行线连接阵点后得到的用来描述原子或原子团在晶体中排列方式空间几何格架。
晶体结构=空间点阵(14种布拉菲点阵)+基元(对应的物理实体:原子或原子团)
单胞、7大晶系、14布拉菲点阵Unit cell、Crystal System、Bravais Lattices
单胞Unit Cell
晶胞:从晶格中选出一个能完全反应晶格特征的最小几何单元。
三维晶胞是由轴 a、b、c 和轴间角α、β γ定义的平行六面体。几何考虑表明,只有 7 种可能的唯一晶格参数,导致 7 个可能的晶胞的组合形状——七大晶系。
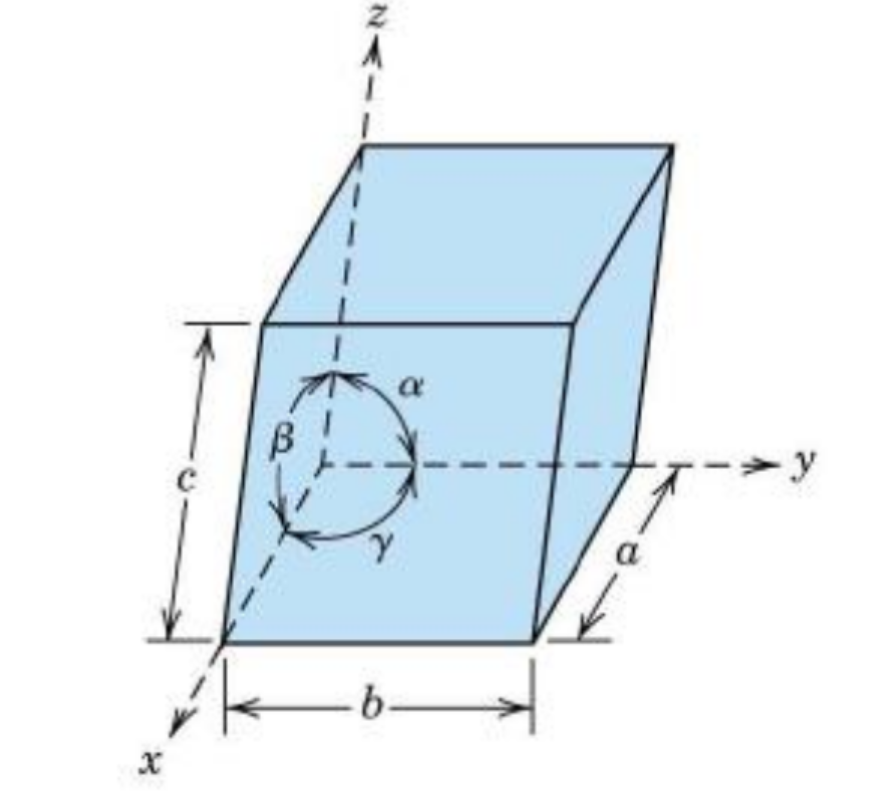
七大晶系Crystal System
7大晶系基于 7 个独特晶胞形状。
每个晶系和相应的晶胞都由不同从晶胞参数的组合定义:a、b、c和α、β、γ


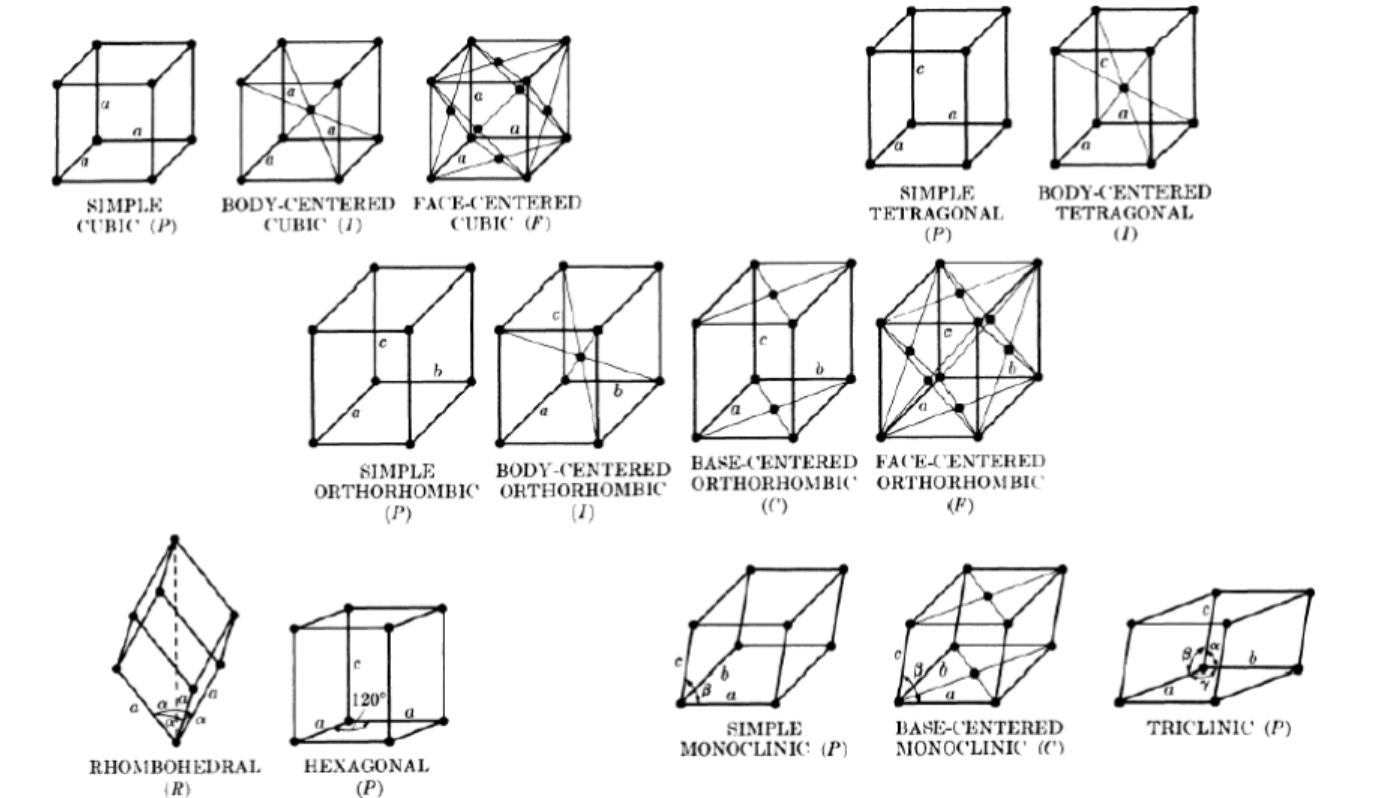
布拉菲点阵Bravais Lattices
7 种可能的晶体系统 + 4 种可能的放置位点→ 14 个晶格 (Bravais Lattices)
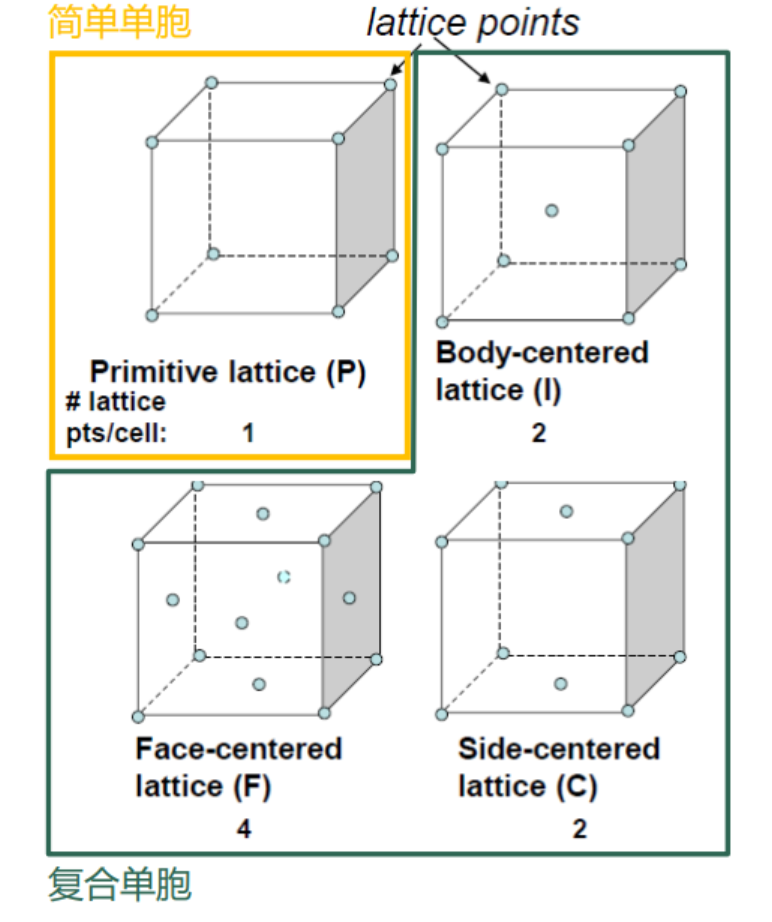
4种点阵:
- 简单点阵P:只在六面体八个顶点分布阵点
- 体心点阵I:中心还有阵点
- 底心点阵A、B或C:只在一组对应面中心有阵点
- 面心点阵F:在所有对应面中心有阵点
后3种有心点阵统称为复杂点阵。
4(placements) × 7(Crystal systems) = 28→14(Bravis lattice) 【实际发现很多点阵不存在,而且有相互等效的点阵】
晶向(族)、晶面(族)、晶带轴Crystallographic Directions、Crystallographic Planes、Zone Axis
晶向Crystallographic Directions
空间中某一点的指标,可以从原点作到该点的向量r,向量r可以用基础矢量a,b,c表示: r = u a + v b + w c \bold r=u\bold a+v\bold b+w\bold c r=ua+vb+wc,这里u,v,w是阵点的坐标,也称为晶向指数(可正可负可为零)。
晶向指数建立方法如下:
- 建系
- 过原点作直线OP平行于待求晶向,确定出P的三坐标
- 化整,加方括号:[uvw]为待定晶向的晶向指数(负数在指数上方加一负号)
晶向指数性质:
- 一个晶向指数代表所有方向一致、相互平行的晶向
- 两晶向平行但是方向相反:晶向指数数字相同,符号相反
- 晶向族:原子排列状况相同,但是空间位向不同的各个晶向,用
<uvw>表示(晶向指数数字相同,符号不同)。
比如<121>:[121][112][211][]… - 立方晶系中,改变晶向指数的数字顺序,原子排列状况完全相同,都属于一个晶向族。
晶面Planes in Crystals
晶体(或晶格)可以被认为是一堆平行原子层(或晶格平面)重复固定距离 (D)
可以绘制无限的平行平面集每个晶体都有独特的原子分布,平面密度和平面间距 (D)
这些平面可以使用 Miller 索引系统彼此索引并区分
晶面指数用3个整数+圆括号(hkl)表示。
晶面指数建立方法如下:
- 建系,O选在离待定晶面最近的阵点上
- 求待定晶面在三个坐标轴上的截距值(若平行,则截距值为∞;若与负方向相截,则截距值为负数)
- 求截距值的倒数
- 化为互质,加圆括号:(hkl)为待定晶面的晶面指数(负数在指数上方加一负号)
晶面指数性质:
- 一个晶面指数代表一组相互平行的晶面,经过所有阵点
- 平行晶面:晶面指数相同/数字相同,符号相反
- 晶面族:晶面上原子排列状况相同,晶面间距相同但是空间位向不同的各组晶面,用
{hkl}表示(晶面指数数字相同,符号不同)。
比如{110}:
( 110 ) ( 1 ˉ 10 ) ( 1 1 ˉ 0 ) ( 1 ˉ 1 ˉ 0 ) (110)(\bar110)(1\bar10)(\bar1\bar10) (110)(1ˉ10)(11ˉ0)(1ˉ1ˉ0)
( 101 ) ( 1 ˉ 01 ) ( 10 1 ˉ ) ( 1 ˉ 0 1 ˉ ) (101)(\bar101)(10\bar1)(\bar10\bar1) (101)(1ˉ01)(101ˉ)(1ˉ01ˉ)
( 011 ) ( 0 1 ˉ 1 ) ( 01 1 ˉ ) ( 0 1 ˉ 1 ˉ ) (011)(0\bar11)(01\bar1)(0\bar1\bar1) (011)(01ˉ1)(011ˉ)(01ˉ1ˉ) - 立方晶系中,相同指数的晶面晶向互相垂直
六方晶系中,三轴指数和四轴指数的相互转化
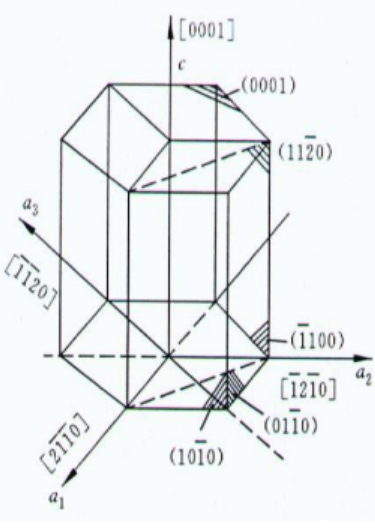
三轴指的是 a 1 , a 2 , c a_1,a_2,c a1,a2,c三轴。
四轴指的是 a 1 , a 2 , a 3 , c a_1,a_2,a_3,c a1,a2,a3,c四轴
晶向指数的转化
三轴晶向指数:[UVW]
四轴晶向指数:[uvtw]
u+v+t=0,W=w
用三轴表示和用四轴表示的是同一条直线:
U a 1 + V a 2 + W z = u a 1 + v a 2 + t a 3 + w z Ua_1+Va_2+Wz=ua_1+va_2+ta_3+wz Ua1+Va2+Wz=ua1+va2+ta3+wz
U a 1 + V a 2 = u a 1 + v a 2 + ( u + v ) ( a 1 + a 2 ) Ua_1+Va_2=ua_1+va_2+(u+v)(a_1+a_2) Ua1+Va2=ua1+va2+(u+v)(a1+a2)
U a 1 + V a 2 = u a 1 + v a 2 + u a 1 + u a 2 + v a 1 + v a 2 = 2 u a 1 + 2 v a 2 + u a 2 + v a 1 Ua_1+Va_2=ua_1+va_2+ua_1+ua_2+va_1+va_2=2ua_1+2va_2+ua_2+va_1 Ua1+Va2=ua1+va2+ua1+ua2+va1+va2=2ua1+2va2+ua2+va1
U = 2 u + v , V = 2 v + u U=2u+v,V=2v+u U=2u+v,V=2v+u
晶面指数的转化
三轴晶向指数:(hkl)
四轴晶向指数:(hkil)
i=-h-k
晶带轴Zone Axis
满足[u v w]与所有晶面法线垂直 h u + k v+l w = 0 (晶带轴定律)
一个晶带轴含有无数个晶面,但是只有低指数晶面有实际意义。
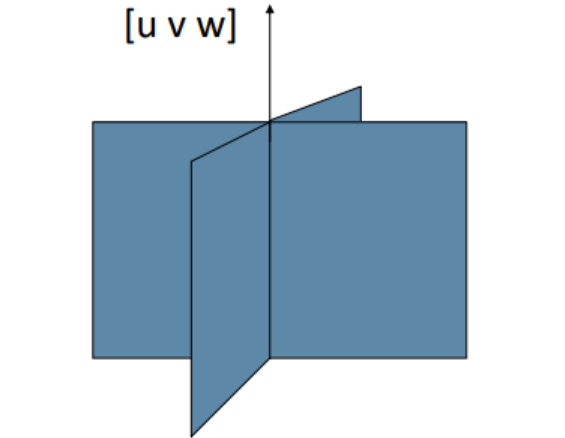
求解晶带轴:
已知两个晶面,求过这两个晶面的晶带轴。
两个晶面的晶面指数为 ( h 1 , k 1 , l 1 ) , ( h 2 , k 2 , l 2 ) (h_1,k_1,l_1),(h_2,k_2,l_2) (h1,k1,l1),(h2,k2,l2),那么两个晶面的法线的晶向就是 [ h 1 , k 1 , l 1 ] , [ h 2 , k 2 , l 2 ] [h_1,k_1,l_1],[h_2,k_2,l_2] [h1,k1,l1],[h2,k2,l2],用向量叉乘求同时垂直这两个法线的直线的晶向:
( i j k h 1 k 1 l 1 h 2 k 2 l 2 ) = ( k 1 l 1 k 2 l 2 ) i − ( h 1 l 1 h 2 l 2 ) j + ( h 1 k 1 h 2 k 2 ) k = ( k 1 l 2 − k 2 l 1 ) i + ( l 1 h 2 − l 2 h 1 ) j + ( h 1 k 2 − h 2 k 1 ) k \begin{pmatrix} i & j& k \\ h_1& k_1& l_1\\ h_2& k_2 & l_2 \end{pmatrix}\\= \begin{pmatrix} k_1& l_1\\ k_2 & l_2 \end{pmatrix}i-\begin{pmatrix} h_1& l_1\\ h_2& l_2 \end{pmatrix}j+\begin{pmatrix} h_1& k_1\\ h_2& k_2 \end{pmatrix}k\\ =(k_1l_2-k_2l_1)i+(l_1h_2-l_2h_1)j+(h_1k_2-h_2k_1)k ih1h2jk1k2kl1l2 =(k1k2l1l2)i−(h1h2l1l2)j+(h1h2k1k2)k=(k1l2−k2l1)i+(l1h2−l2h1)j+(h1k2−h2k1)k
晶体的对称性、空间群Symmetry of Crystal、Space Group
晶体的对称性Symmetry of Crystal
对称操作(Symmetry operation):
能够使对称物体(或图形)中的各个相同部分间做有规律重复的变化动作。
对称要素(Symmetry elements):
进行对称变换时所凭借的几何要素——点、线、面等。
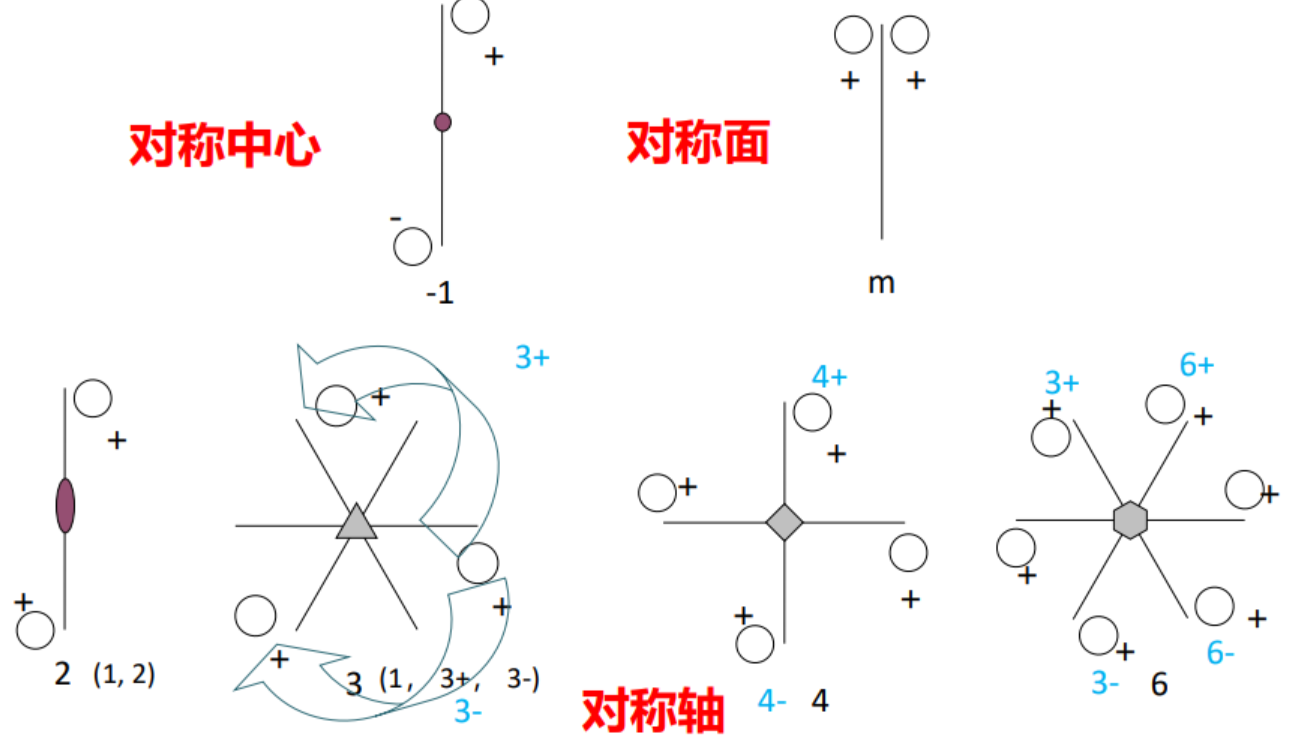
宏观对称性
-
对称中心 (Symmetry center,国际符号: 1 ˉ \bar 1 1ˉ):对称操作为对这个点的倒反
-
对称面(Symmetry plane, 国际符号: m):对称操作为对这个面的反映
-
对称轴(Symmetry axis, 国际符号:n):对称操作为围绕此直线旋转
- 晶体对称定律:晶体中,只可能出现轴次为1、2、3、4、6次的对称轴
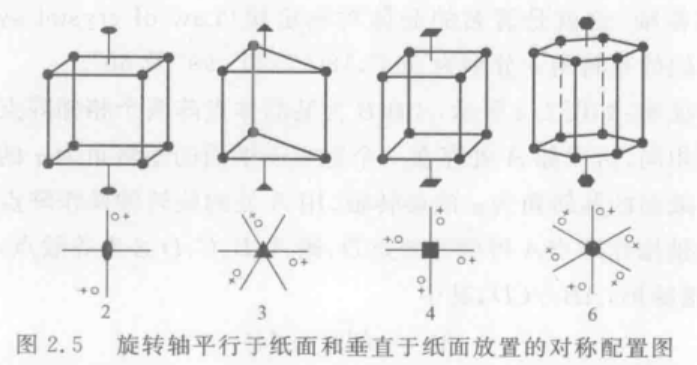
这里的空心圆圈表示一般等效点的位置,”+“表示此点位于纸面之上。
-
倒反轴(Rotation-inversion axis, 简称反轴,国际符号: n ˉ \bar n nˉ)(复合对称操作,由一个旋转轴加轴上的一个对称中心组成)

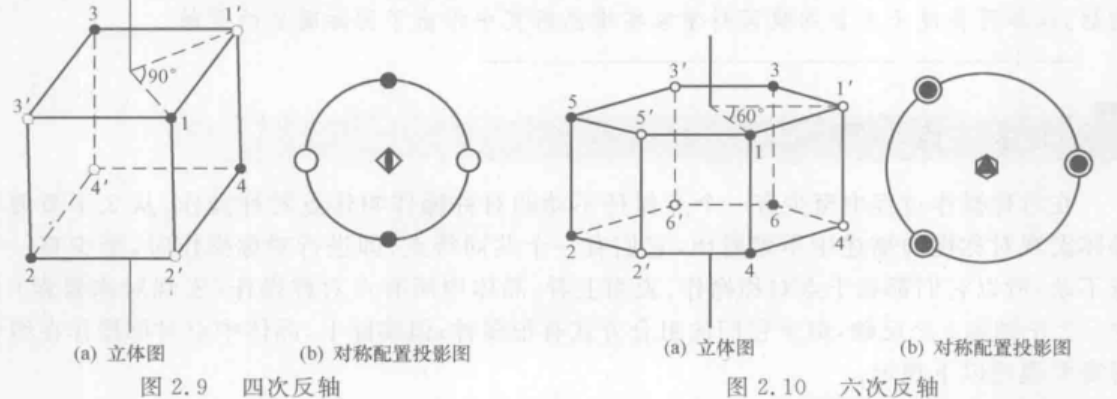
实心点和空心点表示不同高度的点。数字‘表示旋转后的点,再进行对称中心
微观对称性
1.平移轴(Translation axis)
平移轴为一直线,晶体结构沿该直线移动一定距离可使晶体复原。
空间点阵中任意一个行列都是平移轴。
晶体复原:晶体沿着空间点阵中任意一个行列移动一个或多个阵点间距都可以让每一个阵点和相同的阵点重合。
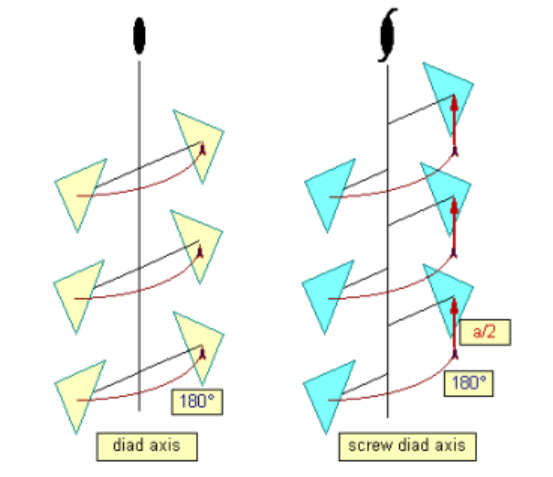
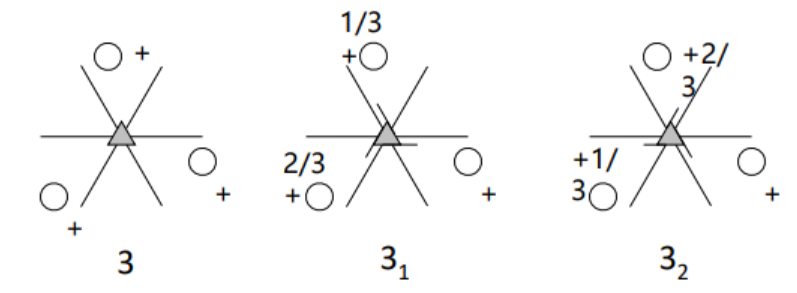
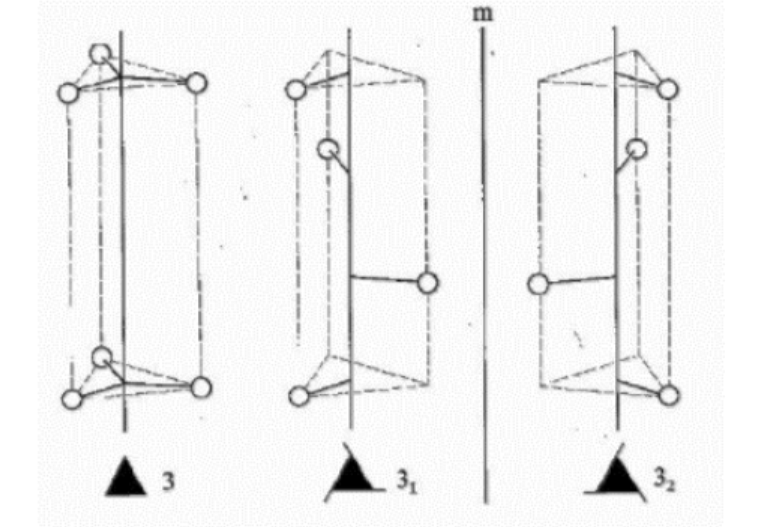
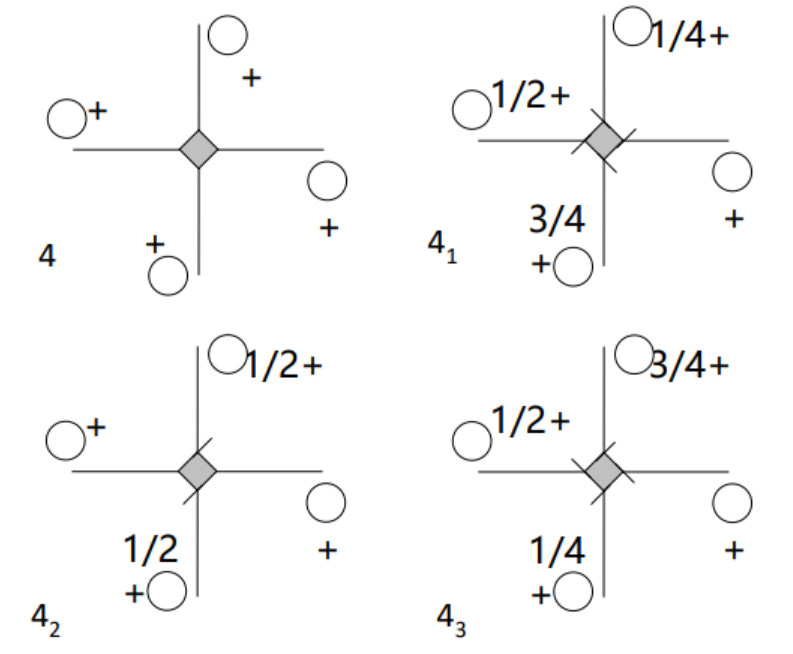
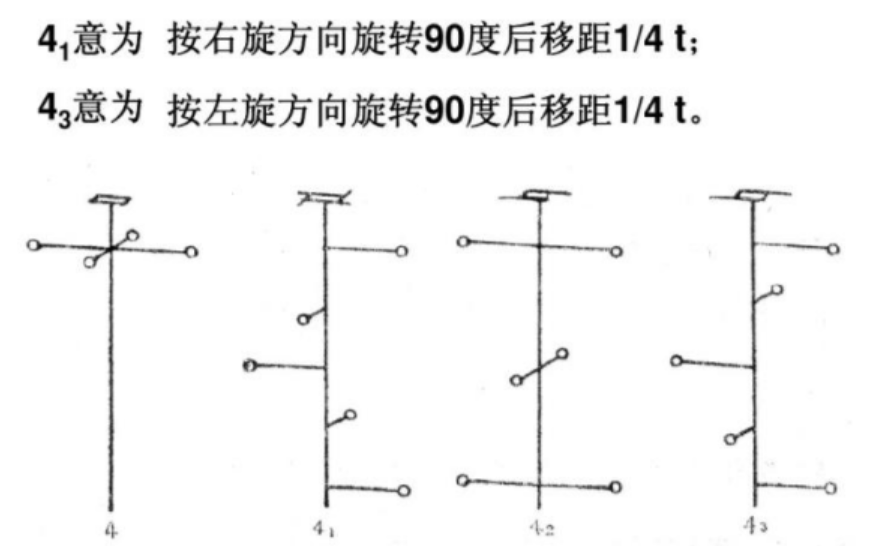
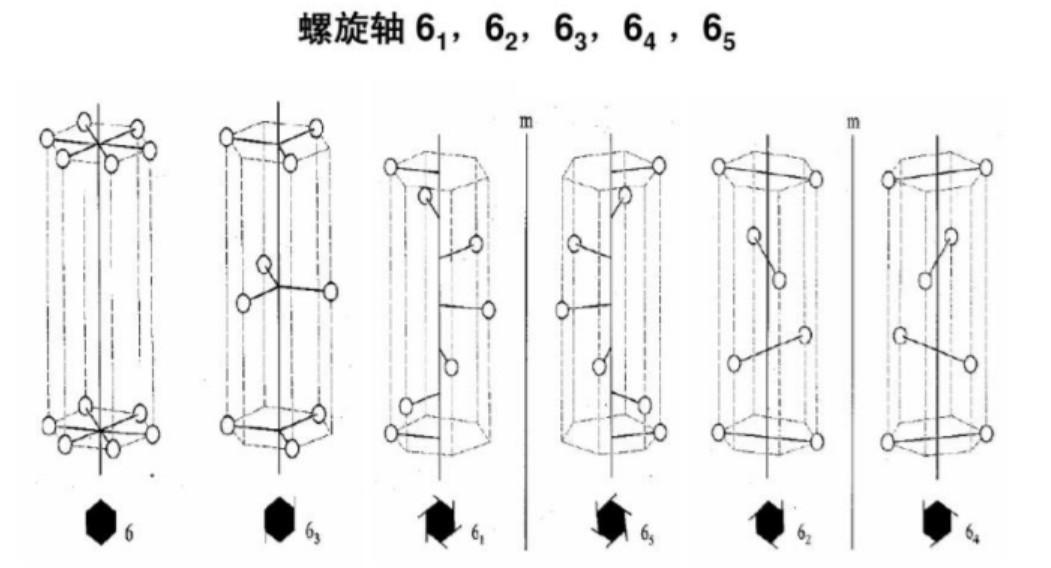
2.螺旋轴(Screw axis)= 平移 + 旋转
包括一个n次旋转轴和与此平行并有一定移距(τ=s/n)的平移操作。操作顺序可以互换。
n为旋转轴的轴次,根据晶体对称定律,n=1,2,3,4,6;s≤n,且只能取1,2,3,4,6。
螺旋轴根据其轴次和平移移距的不同可以分为12种,其国际符号为:

大的数字n表示轴次n,数字角标i表示在此轴上移动i个原子间距。
其中 1 1 1_1 11表示旋转一周并在轴上移动一个原子间距,相当于没动,故去掉这种情况,实际有效的螺旋轴只有11种。
下面给出螺旋轴的投影配置图,所有旋转都用右旋替代。
二次螺旋轴
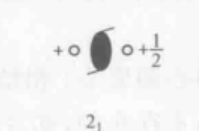
二次螺旋轴先把阵点(用小空心圆代替)从左旋到右,再沿着轴往上挪了1/2个原子间距,所以右边对应的小空心圆比纸面高了+1/2。
三次螺旋轴
4次螺旋旋转轴
6次螺旋旋转轴
3.滑移面(Glide plane)= 平移 + 镜面
镜面反映+沿着平行于镜面的平移,平移方向可为单胞的某一棱边a、b、c〔轴向滑移a、b、c),或单胞的面或体对角线方向(对角滑移n或d〕;量为该周期的1/2。

空间群Space Group
空间群:晶体学种所有对称要素(宏观对称+微观对称)组合的所有可能性构成的集合。
能使晶体结构复原的所有对称变换的集合。
空间群符号 L S 1 S 2 S 3 L_{S1S2S3} LS1S2S3
运用以下规则,可以从对称元素获得空间群符号。
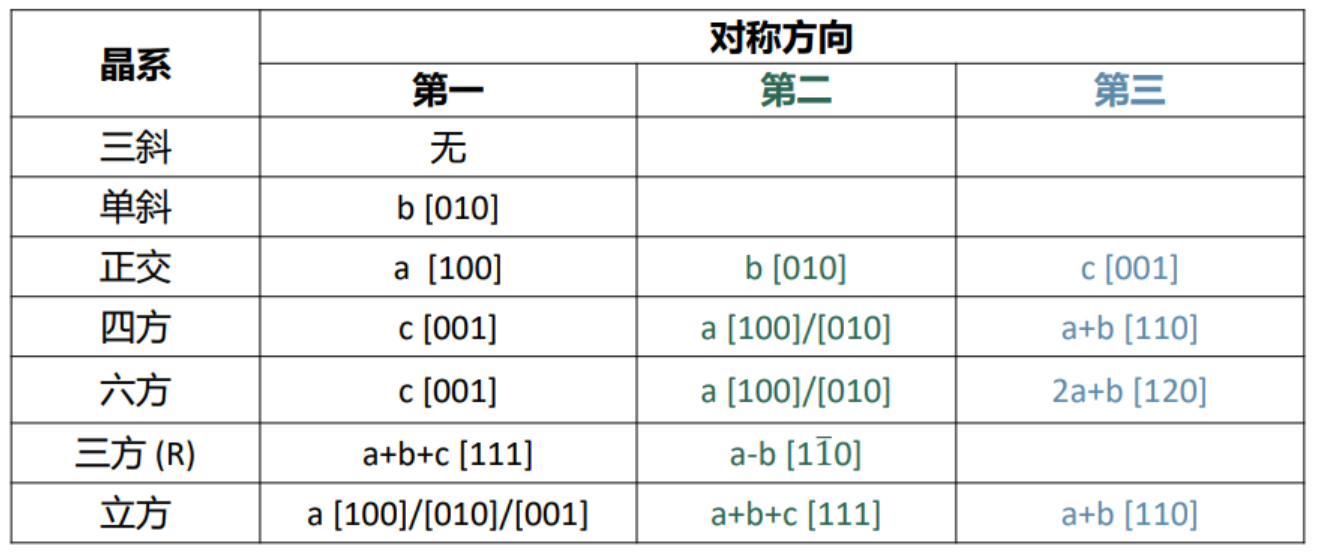
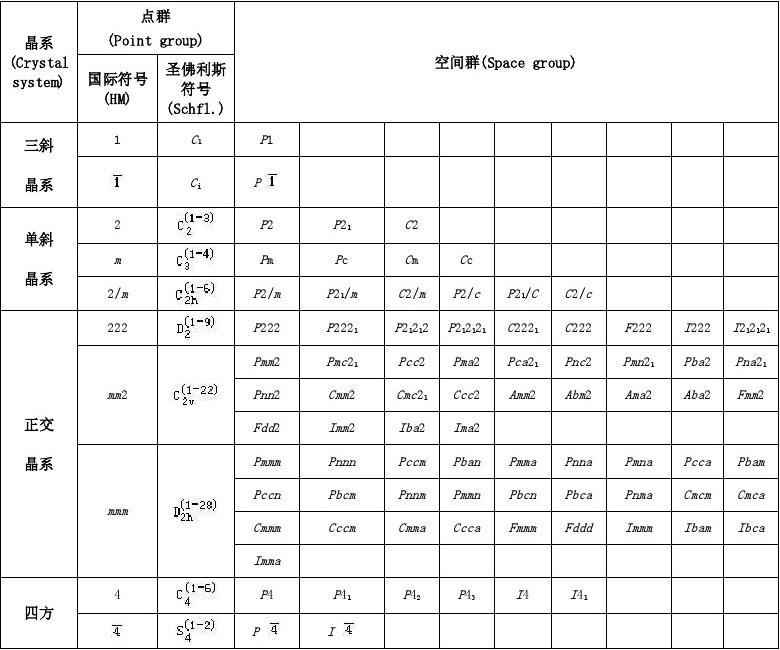
- 第一字母(L)是点阵描述符号,指明点阵带心类型: P, I, F, C, A, B。
- 其余三个符号(S1S2S3)表示在特定方向(对每种晶系分别规定)上的对称元素。后一部分与点群的国际符号基本相同,不同的是那三个特定方向上的对称要素取自晶胞中对应方向上对称程度最高的那种对称要素。
- 如果没有二义性可能,常用符号的省略形式 (如Pm,而不用写成P1m1)。
- 由于不同的晶轴选择和标记,同一个空间群可能有几种不同的符号。如P21/c,如
滑移面选为在a方向,符号为P21/a;如滑移面选为对角滑移,符号为P21/n。


相关文章:

【笔记】材料分析测试:晶体学
晶体与晶体结构Crystal and Crystal Structure 1.晶体主要特征 固态物质可以分为晶态和非晶态两大类,分别称为晶体和非晶体。 晶体和非晶体在微观结构上的区别在于是否具有长程有序。 晶体(长程有序)非晶(短程有序)…...

飞塔Fortigate7.4.4的DNS劫持功能
基础网络配置、上网策略、与Server的VIP配置(略)。 在FortiGate上配置DNS Translation,将DNS请求结果为202.103.12.2的DNS响应报文中的IP地址修改为Server的内网IP 10.10.2.100。 config firewall dnstranslationedit 1set src 2.13.12.2set…...

Unity 设计模式 之 行为型模式 -【状态模式】【观察者模式】【备忘录模式】
Unity 设计模式 之 行为型模式 -【状态模式】【观察者模式】【备忘录模式】 目录 Unity 设计模式 之 行为型模式 -【状态模式】【观察者模式】【备忘录模式】 一、简单介绍 二、状态模式(State Pattern) 1、什么时候使用状态模式 2、使用状态模式的…...

【RabbitMQ】RabbitMQ 的概念以及使用RabbitMQ编写生产者消费者代码
目录 1. RabbitMQ 核心概念 1.1生产者和消费者 1.2 Connection和Channel 1.3 Virtual host 1.4 Queue 1.5 Exchange 1.6 RabbitMO工作流程 2. AMQP 3.RabbitMO快速入门 3.1.引入依赖 3.2.编写生产者代码 3.3.编写消费者代码 4.源码 1. RabbitMQ 核心概念 在安装…...

openmv与stm32通信
控制小车视觉循迹使用 OpenMV 往往是不够的。一般使用 OpenMV 对图像进行处理,将处理过后的数据使用串口发送给STM32,使用STM32控制小车行驶。本文主要讲解 OpenMV 模块与 STM32 间的串口通信以及两种循迹方案,分别是划分检测区域和线性回归。…...
C++ STL全面解析:六大核心组件之一----序列式容器(vector和List)(STL进阶学习)
目录 序列式容器 Vector vector概述 vector的迭代器 vector的数据结构 vector的构造和内存管理 vector的元素操作 List List概述 List的设计结构 List的迭代器 List的数据结构 List的内存构造 List的元素操作 C标准模板库(STL)是一组高效的…...

【c数据结构】OJ练习篇 帮你更深层次理解链表!(相交链表、相交链表、环形链表、环形链表之寻找环形入口点、判断链表是否是回文结构、 随机链表的复制)
目录 一. 相交链表 二. 环形链表 三. 环形链表之寻找环形入口点 四. 判断链表是否是回文结构 五. 随机链表的复制 一. 相交链表 最简单粗暴的思路,遍历两个链表,分别寻找是否有相同的对应的结点。 我们对两个链表的每个对应的节点进行判断比较&…...
)
微软开源GraphRAG的使用教程(最全,非常详细)
GraphRAG的介绍 目前微软已经开源了GraphRAG的完整项目代码。对于某一些LLM的下游任务则可以使用GraphRAG去增强自己业务的RAG的表现。项目给出了两种使用方式: 在打包好的项目状态下运行,可进行尝试使用。在源码基础上运行,适合为了下游任…...
初始化项目)
使用Refine构建项目(1)初始化项目
要初始化一个空的Refine项目,你可以使用Refine提供的CLI工具create-refine-app。以下是初始化步骤: 使用npx命令: 在命令行中运行以下命令来创建一个新的Refine项目: npx create-refine-applatest my-refine-project这将引导你通过…...

【Docker】安装及使用
1. 安装Docker Desktop Docker Desktop是官方提供的桌面版Docker客户端,在Mac上使用Docker需要安装这个工具。 访问 Docker官方页面 并下载Docker Desktop for Mac。打开下载的.dmg文件,并拖动Docker图标到应用程序文件夹。安装完成后,打开…...

[大语言模型-论文精读] 以《黑神话:悟空》为研究案例探讨VLMs能否玩动作角色扮演游戏?
1. 论文简介 论文《Can VLMs Play Action Role-Playing Games? Take Black Myth Wukong as a Study Case》是阿里巴巴集团的Peng Chen、Pi Bu、Jun Song和Yuan Gao,在2024.09.19提交到arXiv上的研究论文。 论文: https://arxiv.org/abs/2409.12889代码和数据: h…...

提升动态数据查询效率:应对数据库成为性能瓶颈的优化方案
引言 在现代软件系统中,数据库性能是决定整个系统响应速度和处理能力的关键因素之一。然而,当系统负载增加,特别是在高并发、大数据量场景下,数据库性能往往会成为瓶颈,导致查询响应时间延长,影响用户体验…...

Prometheus+grafana+kafka_exporter监控kafka运行情况
使用Prometheus、Grafana和kafka_exporter来监控Kafka的运行情况是一种常见且有效的方案。以下是详细的步骤和说明: 1. 部署kafka_exporter 步骤: 从GitHub下载kafka_exporter的最新版本:kafka_exporter项目地址(注意ÿ…...

在vue中:style 的几种使用方式
在日常开发中:style的使用也是比较常见的: 亲测有效 1.最通用的写法 <p :style"{fontFamily:arr.conFontFamily,color:arr.conFontColor,backgroundColor:arr.conBgColor}">{{con.title}}</p> 2.三元表达式 <a :style"{height:…...

商城小程序后端开发实践中出现的问题及其解决方法
前言 商城小程序后端开发中,开发者可能会面临多种问题。以下是一些常见的问题及其解决方法: 一、性能优化 问题:随着用户量的增加和功能的扩展,商城小程序可能会出现响应速度慢、处理效率低的问题。 解决方法: 对数…...

阿里Arthas-Java诊断工具,基本操作和命令使用
Arthas 是阿里巴巴开源的一款Java诊断工具,深受开发者喜爱。它可以帮助开发者在不需要修改代码的情况下,对运行中的Java程序进行问题诊断和性能分析。 软件具体使用方法 1 启动 Arthas,此时可能会出现好几个jvm的进程号,输入序号…...

Go 1.19.4 路径和目录-Day 15
1. 路径介绍 存储设备保存着数据,但是得有一种方便的模式让用户可以定位资源位置,操作系统采用一种路径字符 串的表达方式,这是一棵倒置的层级目录树,从根开始。 相对路径:不是以根目录开始的路径,例如 a/b…...

jEasyUI 创建标签页
jEasyUI 创建标签页 jEasyUI(jQuery EasyUI)是一个基于jQuery的框架,它为Web应用程序提供了丰富的用户界面组件。标签页(Tabs)是jEasyUI中的一个常用组件,用于在一个页面内组织多个面板,用户可…...

鸿蒙HarmonyOS开发:一次开发,多端部署(界面级)天气应用案例
文章目录 一、布局简介二、典型布局场景三、侧边栏 SideBarContainer1、子组件2、属性3、事件 四、案例 天气应用1、UX设计2、实现分析3、主页整体实现4、具体代码 五、运行效果 一、布局简介 布局可以分为自适应布局和响应式布局,二者的介绍如下表所示。 名称简介…...

使用 Python 模拟光的折射,反射,和全反射
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
