L3 逻辑回归
- 🍨 本文为🔗365天深度学习训练营 中的学习记录博客
- 🍖 原作者:K同学啊
在周将使用 LogisticRegression 函数对经典的鸢尾花 (Iris) 数据集进行分类。将详细介绍逻辑回归的数学原理。
1. 逻辑回归的数学原理
逻辑回归是一种线性分类算法,常用于二分类问题。它的核心思想是通过将线性回归模型的输出通过一个 Sigmoid 函数映射到一个 0 到 1 之间的概率值,从而进行分类。
1.1 线性模型
逻辑回归的线性模型与线性回归相似,其形式为:
z = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_n x_n z=β0+β1x1+β2x2+⋯+βnxn
其中:
- ( z ) 是线性组合的输出,
- ( x 1 x_1 x1, x 2 x_2 x2, … \dots …, x n x_n xn) 是特征变量,
- ( β 0 \beta_0 β0 ) 是截距(常数项),
- ( β 1 , … , β n \beta_1, \dots, \beta_n β1,…,βn ) 是特征变量的系数。
1.2 Sigmoid 函数
线性模型输出 ( z ) 之后,通过 Sigmoid 函数将其转化为概率:
y ^ = σ ( z ) = 1 1 + e − z \hat{y} = \sigma(z) = \frac{1}{1 + e^{-z}} y^=σ(z)=1+e−z1
Sigmoid 函数的输出值是一个概率,范围在 0 到 1 之间。当概率 ( y ^ ≥ 0.5 \hat{y} \geq 0.5 y^≥0.5) 时,我们预测为正类(1),否则预测为负类(0)。
1.3 损失函数(对数损失)
为了找到最优的系数 ( β \beta β ),我们需要最小化损失函数。逻辑回归的损失函数为对数损失函数(log loss):
L ( β ) = − 1 m ∑ i = 1 m [ y ( i ) log ( y ^ ( i ) ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] L(\beta) = - \frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}) \right] L(β)=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
其中:
- ( m ) 是样本数,
- ( y ( i ) y^{(i)} y(i) ) 是第 ( i i i ) 个样本的真实标签,
- ( y ^ ( i ) \hat{y}^{(i)} y^(i)) 是第 ( i i i ) 个样本的预测概率。
通过梯度下降法或其他优化算法,逻辑回归模型可以根据最小化该损失函数来找到最优的参数 ( β \beta β )。
2. LogisticRegression 函数介绍
LogisticRegression(penalty='l2', # 正则化类型,'l1', 'l2', 'elasticnet', 'none'dual=False, # 双对偶或原始方法tol=0.0001, # 优化过程的容差C=1.0, # 正则化强度的倒数,较小的值表示较强的正则化fit_intercept=True, # 是否拟合截距项intercept_scaling=1, # 拦截(截距)的缩放系数class_weight=None, # 给定类别的权重,'balanced' 或 dictrandom_state=None, # 随机数种子solver='lbfgs', # 优化算法,{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}max_iter=100, # 最大迭代次数multi_class='auto', # 处理多类分类问题的方法,{'auto', 'ovr', 'multinomial'}verbose=0, # 是否在训练过程中输出日志信息warm_start=False, # 是否使用上次调用的解作为初始解n_jobs=None, # 并行处理的作业数量l1_ratio=None # 混合正则化的弹性网络的l1比例
)
3. 鸢尾花数据分类
鸢尾花数据集是一个经典的多分类数据集,包含 150 个样本,分为 3 类(Setosa、Versicolor、Virginica),每类 50 个样本。每个样本有 4 个特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
以下是完整的代码实现:
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.linear_model import LogisticRegression# 1. 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征矩阵
y = iris.target # 目标变量# 2. 特征标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 3. 划分训练集和测试集(80% 训练集,20% 测试集)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)# 4. 逻辑回归模型
model = LogisticRegression(max_iter=200)
model.fit(X_train, y_train)# 5. 模型预测
y_pred = model.predict(X_test)# 6. 模型评估
accuracy = accuracy_score(y_test, y_pred)
print(f"模型的准确率: {accuracy:.2f}")# 打印分类报告
print("分类报告:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))# 打印混淆矩阵
print("混淆矩阵:")
print(confusion_matrix(y_test, y_pred))

4. 总结
本周学习了逻辑回归的数学原理,并通过鸢尾花数据集展示了如何使用 LogisticRegression 进行多分类任务。为后续学习打下基础。
相关文章:

L3 逻辑回归
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 在周将使用 LogisticRegression 函数对经典的鸢尾花 (Iris) 数据集进行分类。将详细介绍逻辑回归的数学原理。 1. 逻辑回归的数学原理 逻辑回归是一种线性分…...

Flink系列知识之:Checkpoint原理
Flink系列知识之:Checkpoint原理 在介绍checkpoint的执行流程之前,需要先明白Flink中状态的存储机制,因为状态对于检查点的持续备份至关重要。 State Backends分类 下图显示了Flink中三个内置的状态存储种类。MemoryStateBackend和FsState…...
智算中心动环监控:构建高效、安全的数字基础设施@卓振思众
在当今快速发展的数字经济时代,智算中心作为人工智能和大数据技术的核心支撑设施,正日益成为各行业实现智能化转型的重要基石。为了确保这些高性能计算环境的安全与稳定,卓振思众动环监控应运而生,成为智算中心管理的重要组成部分…...

PyTorch VGG16手写数字识别教程
手写数字识别教程:使用PyTorch和VGG16 1. 环境准备 确保你已安装以下库: pip install torch torchvision2. 导入必要的库 import torch import torch.nn as nn import torch.optim as optim import torchvision.transforms as transforms import tor…...

安卓13删除下拉栏中的设置按钮 android13删除设置按钮
总纲 android13 rom 开发总纲说明 文章目录 1.前言2.问题分析3.代码分析4.代码修改5.编译6.彩蛋1.前言 顶部导航栏下拉可以看到,底部这里有个设置按钮,点击可以进入设备的设置页面,这里我们将更改为删除,不同用户通过这个地方进入设置。也就是下面这个按钮。 2.问题分析…...

FDA辅料数据库在线免费查询-药用辅料
在药物制剂的研制过程中,需要确定这些药用辅料的安全用量。而美国食品药品监督管理局(FDA)的辅料数据库(IID)提供了其制剂研发中的关键参考资源,使得更多的医药研发相关人员及企业单位节省试验环节及时间成…...

git pull 报错 refusing to merge unrelated histories
这个对我来说非常常见,因为我都是先由本地项目,再想着传到github上去。 在本地项目中执行 git init git add . git commit -m “xxx” 在github上创建项目,添加了 README.md 文件。 git remote add origin https://github.com/raoxiaoya/x…...

STM32G431RBT6(蓝桥杯)串口(发送)
一、基础配置 (1) PA9和PA10就是串口对应在单片机上的端口 注意:一定要先选择PA9的TX和PA10的RX,再去打开异步的模式 (2) 二、查看单片机的端口连接至电脑的哪里 (1)此电脑->右击属性 (2)找到端…...

使用 typed-rest-client 进行 REST API 调用
typed-rest-client 是一个用于 Node.js 的库,它提供了一种类型安全的方式来与 RESTful API 进行交互。其主要功能包括: 安装 typed-rest-client 要使用 typed-rest-client,首先需要安装它,可以通过 npm 来安装: $ n…...

在Ubuntu 14.04上安装Solr的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 Solr 是基于 Apache Lucene 的搜索引擎平台。它用 Java 编写,并使用 Lucene 库来实现索引。可以通过各种 REST API&am…...
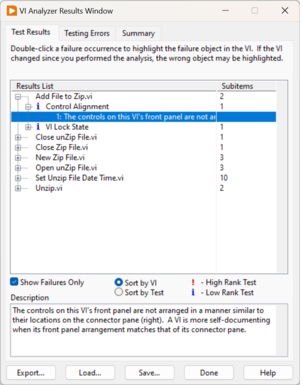
LabVIEW提高开发效率技巧----使用LabVIEW工具
LabVIEW为开发者提供了多种工具和功能,不仅提高工作效率,还能确保项目的质量和可维护性。以下详细介绍几种关键工具,并结合实际案例说明它们的应用。 1. VI Analyzer:自动检查代码质量 VI Analyzer 是LabVIEW提供的一款强大的工…...
)
Pyspark dataframe基本内置方法(4)
文章目录 Pyspark sql DataFrame相关文章RDDrepartition 重新分区replace 替换sameSemantics dataframe是否相等sample 采样sampleBy 分层采样schema 显示dataframe结构select 查询selectExpr 查询semanticHash 获取哈希值show 展示dataframesort 排序sortWithinPartitions 分区…...

配置win10开电脑时显示可登录账号策略
有1台公用的windows10电脑,电脑上有N多用户,使用人员登录时选择相应的账号登录即可。但在某次使用脚本加固后,发现之前显示的用户都不能显示了。检查加固脚本,是脚本启用了“交互式登录:不显示上次登录”策略。因此&am…...
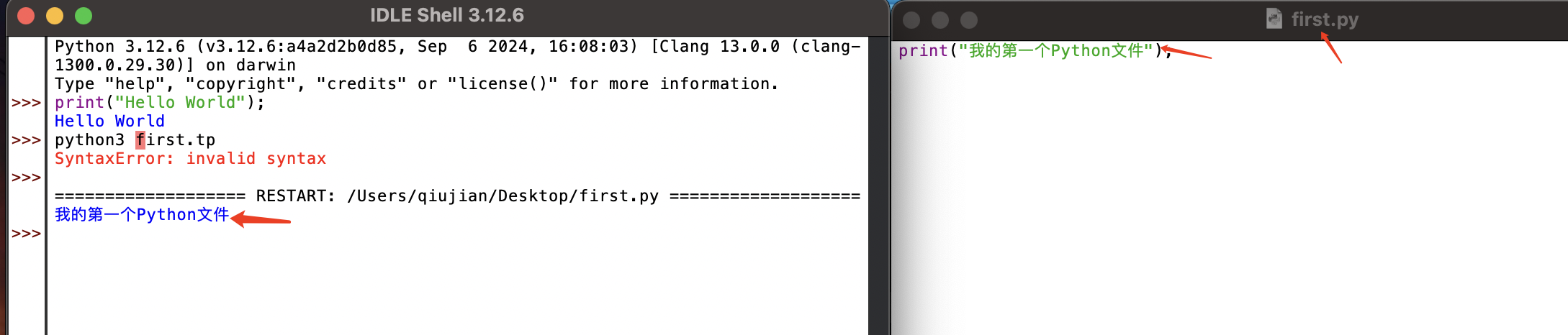
01-Mac OS系统如何下载安装Python解释器
目录 Mac安装Python的教程 mac下载并安装python解释器 如何下载和安装最新的python解释器 访问python.org(受国内网速的影响,访问速度会比较慢,不过也可以去我博客的资源下载) 打开历史发布版本页面 进入下载页 鼠标拖到页面…...

24 C 语言常用的字符串处理函数详解:strlen、strcat、strcpy、strcmp、strchr、strrchr、strstr、strtok
目录 1 strlen 1.1 函数原型 1.2 功能说明 1.3 案例演示 1.4 注意事项 2 strcat 2.1 函数原型 2.2 功能说明 2.3 案例演示 2.4 注意事项 3 strcpy 3.1 函数原型 3.2 功能说明 3.3 案例演示 3.4 注意事项 4 strcmp 4.1 函数原型 4.2 功能说明 4.3 案例演示 …...

数据驱动农业——农业中的大数据
橙蜂智能公司致力于提供先进的人工智能和物联网解决方案,帮助企业优化运营并实现技术潜能。公司主要服务包括AI数字人、AI翻译、埃域知识库、大模型服务等。其核心价值观为创新、客户至上、质量、合作和可持续发展。 橙蜂智农的智慧农业产品涵盖了多方面的功能&…...

学习《分布式》必须清楚的《CAP理论》
分布式的理论基础CAP理论 当学习分布式的redis、mq等中间件时,都会看到有提到CAP。 CAP理论是学习分布式必备的一个概念知识点。 CAP理论由三个特性组成,分别是一致性(Consistency)、可用性(Availability࿰…...

navicat无法连接远程mysql数据库1130报错的解决方法
出现报错:1130 - Host ipaddress is not allowed to connect to this MySQL serve navicat,当前ip不允许连接到这个MySQL服务 解决当前ip无法连接远程mysql的方法 1. 查看mysql端口,并在服务器安全组中放开相应入方向端口后重启服务器 sud…...

JetPack01- LifeCycle 监听Activity或Fragment的生命周期
前提 阅读本文的前提是要了解观察者模式。本文没有讲述反射相关的内容,功能中有使用反射。 简介 监听Activity/Fragment的生命周期,使用观察者模式,Activity/Fragment是被观察者。 监听的生命周期有onCreate、onStart、onResume、onPause…...

OpenCSG推出StarShip SecScan:AI驱动的软件安全革新
OpenCSG 导读 如今,IT 技术迅速发展,软件安全不仅是企业稳健运营的基础,更是整个社会经济体系安全的保障。加强软件安全,尤其是在开发阶段识别和修补漏洞,是企业必须重视的问题。国际数据公司(IDC…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

【AI大模型】Transformer架构到底是什么?
引言 —— 想象一台能瞬间读懂整本《战争与和平》、精准翻译俳句中的禅意、甚至为你的设计草图生成前端代码的机器——这一切并非科幻,而是过去七年AI领域最震撼的技术革命:Transformer架构创造的奇迹。 当谷歌在2017年揭开Transformer的神秘面纱时&…...
