《机器学习》周志华-CH7(贝叶斯分类)
7.1贝叶斯决策论
对分类任务而言,在所有相关概率已知的理想情形下,贝叶斯决策论考虑如何基于这些概率核误判损失来选择最优的类别标记。

R ( x i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) \begin{equation} R(x_{i}|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_{j}|x) \tag{7.1} \end{equation} R(xi∣x)=j=1∑NλijP(cj∣x)(7.1)

h ∗ h^{*} h∗称为贝叶斯最优分类器
总体风险 R ( h ∗ ) R(h^{*}) R(h∗)称为贝叶斯风险。
1 − R ( h ∗ ) 1-R(h^{*}) 1−R(h∗)反映了分类器所能达到的最佳性能,即模型精度上限。
具体而言,若目标是最小化分类错误率,则误判损失 λ i j \lambda_{ij} λij可写为:
λ i j = { 0 i f i = j 1 o t h e r \lambda_{ij}= \begin{cases} 0 & if \quad i=j \\ 1 & other \\ \end{cases} λij={01ifi=jother
条件风险 R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x)=1-P(c|x) R(c∣x)=1−P(c∣x)
最小化分类错误率的贝叶斯最优分类器为

对每个样本 x x x,选后验概率 P ( c ∣ x ) P(c|x) P(c∣x)最大的类别标记
机器学习所要实现的是基于有限训练样本集尽可能准确地估计出后验概率 P ( c ∣ x ) P(c|x) P(c∣x),主要有两种策略

类的先验概率 P ( c ) P(c) P(c):表达了各类样本所占比例,根据大数定律,训练集包含充分独立样本, P ( c ) P(c) P(c)可通过各类样本出现频率估计。
类的条件概率 P ( x ∣ c ) P(x|c) P(x∣c):由于涉及关于 x x x所有属性的联合概率。直接根据样本估计可能遇到困难,使用频率来估计不可行,因为“未被观测到”与“出现概率为零”通常是不同的。
7.2极大似然估计
估计类条件概率记关于类别 c c c的类条件概率为 P ( x ∣ c ) P(x|c) P(x∣c),假设 P ( x ∣ c ) P(x|c) P(x∣c)具有确定的形式并且被参数向量 θ c \theta_c θc唯一确定,则我们的任务就是利用训练集 D D D估计参数 θ c \theta_c θc,将 P ( x ∣ c ) P(x|c) P(x∣c)记为 P ( x ∣ θ c ) P(x|\theta_c) P(x∣θc)
概率模型的训练过程就是参数估计的过程
参数估计两种不同方案:
- 频率主义学派,认为参数虽然未知,但客观存在,可通过优化似然函数等准则确定参数值。
- 贝叶斯派认为参数是未观察到的随机变量,其本身可有分布,因此可假设服从一个先验分布,然后基于观测到的数据来计算参数的后验分布。
极大似然估计MLE,根据数据采样来估计概率分布
令 D c D_c Dc表示训练集 D D D的第 c c c类样本集合,假设样本独立同分布。
参数 θ c \theta_c θc对数据集 D c D_c Dc的似然说
P ( D c ∣ θ c ) = ∏ x ∈ D c P ( x ∣ θ c ) \begin{equation} P(D_c|\theta_c)=\prod_{x\in{D_{c}}}P(x|\theta_c) \tag{7.9} \end{equation} P(Dc∣θc)=x∈Dc∏P(x∣θc)(7.9)
对 θ c \theta_c θc进行极大似然估计,就是去寻找最大化似然 P ( D c ∣ θ c ) P(D_c|\theta_c) P(Dc∣θc)的参数值 θ c ^ \hat{\theta_c} θc^
(7.9)连乘造成下溢,通常为对数似然(log-likehood)
L L ( θ c ) = l o g P ( D c ∣ θ c ) = ∑ x ∈ D c l o g P ( x ∣ θ c ) \begin{equation} LL(\theta_c)=logP(D_{c}|\theta_c) \\ =\sum_{x\in{D_c}}logP(x|\theta_c) \tag{7.10} \end{equation} LL(θc)=logP(Dc∣θc)=x∈Dc∑logP(x∣θc)(7.10)
此时参数 θ c \theta_c θc的极大似然估计 θ c ^ \hat{\theta_c} θc^为
θ c ^ = a r g m a x θ c L L ( θ c ) \begin{equation} \hat{\theta_c}=\underset{\theta_c}{argmax}LL(\theta_c) \tag{7.11} \end{equation} θc^=θcargmaxLL(θc)(7.11)

估计结果的准确性严重依赖所假设的概率分布形式是否符合潜在的真实数据分布。
7.3朴素贝叶斯分类器
贝叶斯公式来估计后验概率 P ( c ∣ x ) P(c|x) P(c∣x)困难在于 P ( x ∣ c ) P(x|c) P(x∣c)是所有属性的联合概率,难以从有限训练样本直接估计。
朴素贝叶斯分类器采用“属性条件独立性假设”对已知类别,假设所有属性相互独立,假设每个属性独立地对分类结果发生影响

朴素贝叶斯分类器的训练过程就是基于训练集 D D D来估计类先验概率 P ( c ) P(c) P(c),并为每个属性来估计条件概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c)
D c D_c Dc表示训练集 D D D中第 c c c类集合,样本充足,则类先验概率:
P ( c ) = ∣ D c ∣ ∣ D ∣ \begin{equation} P(c)=\frac{|D_c|}{|D|} \tag{7.16} \end{equation} P(c)=∣D∣∣Dc∣(7.16)
离散属性而言, D c , x i D_{c,x_i} Dc,xi表示 D c D_c Dc中在第 i i i个属性上取值为 x i x_i xi的样本组成的集合,则条件概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c):
P ( x i ∣ c ) = ∣ D c , x i ∣ ∣ D c ∣ \begin{equation} P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|} \tag{7.17} \end{equation} P(xi∣c)=∣Dc∣∣Dc,xi∣(7.17)

下面用西瓜数据集3.0训练一个朴素贝叶斯分类器,对测试例“测1”进行分类





需注意,若某个属性值在训练中没有与某个类同时出现过,如
P 清脆 ∣ 是 = P ( 敲声 = 清脆 ∣ 好瓜 = 是 ) = 0 8 = 0 P_{清脆|是}=P(敲声=清脆|好瓜=是)=\frac{0}{8}=0 P清脆∣是=P(敲声=清脆∣好瓜=是)=80=0
此时乘积永远是 0 0 0,避免这种情况,在估计概率值时通常进行“平滑”,查用“拉普拉斯修正”
令 N N N表示训练集 D D D中可能的类别数, N i N_i Ni表示第 i i i个属性可能取值

7.4半朴素贝叶斯分类器
人们尝试对属性条件独立性假设进行一定程度的放松。
半朴素贝叶斯分类器基本想法:适当考虑一部分属性间的相互依赖信息,从而既不需要进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
“独依赖估计(One-Dependent Estimator,ODE)” 是半朴素贝叶斯分类器最常用的一种策略。顾名思义,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖一个其他属性,即:

如何确定每个属性的父属性?不同策略的独依赖分类器又不同
所有属性都依赖于同一个属性,称为“超父”, x 1 x_1 x1必是超父属性


AODE(Averaged One-Dependent Estimator) 尝试将每个属性作为超父构建SPODE,然后将那些具有足够训练数据支持的SPODE集成为最终结果,即:

其中 D x i D_{xi} Dxi是第 i i i个属性取值为 x i x_i xi样本集合, m ′ m^{'} m′为阈值常数


AODE无需模型选择,既能通过预计算节省预测时间,也能采取懒惰学习方法在预测时在再进行计数,易于实现增量学习。
7.5贝叶斯网
贝叶斯网(Bayesian network) 亦称“信念网”(belief network),借助有向五环图(Directed Acyclic Graph,简称DAG) 刻画属性依赖关系,并使用条件概率表(Conditional Probability Table,简称CPT)来描述属性联合概率分布。
一个贝叶斯网 B B B 由结构 G G G和参数 θ \theta θ两部分组成, B = < G , θ > B=<G,\theta> B=<G,θ>
网络结构 G G G是一个有向无环图,其中每个结点对应一个属性,两属性有直接依赖关系则由一条边连接
参数 θ \theta θ定量描述这种依赖关系,假设属性 x i x_i xi在 G G G中的父结点集为 π i \pi_{i} πi,则 θ \theta θ包含了每个属性的条件概率表是 θ x i ∣ π i = P B ( x i ∣ π i ) \theta_{x_i|\pi_i}=P_{B}(x_i|\pi_i) θxi∣πi=PB(xi∣πi)

7.5.1结构
贝叶斯网结构有效地表达了属性间的条件独立性,给定父结点集,贝叶斯网假设每个属性与它的非后裔属性独立。
B = < G , θ > B=<G,\theta> B=<G,θ>将属性 x 1 , x 2 , . . . , x d x_1,x_2,...,x_d x1,x2,...,xd的联合概率分布定义为
P B ( x 1 , x 2 , . . . , x d ) = ∏ i = 1 d P B ( x i ∣ π i ) = ∏ i = 1 d θ x i ∣ π i \begin{equation} P_{B}(x_1,x_2,...,x_d)=\prod_{i=1}^{d}P_{B}(x_i|\pi_i)=\prod_{i=1}^{d}\theta_{x_i|\pi_i} \tag{7.26} \end{equation} PB(x1,x2,...,xd)=i=1∏dPB(xi∣πi)=i=1∏dθxi∣πi(7.26)
以图7.2为例,联合概率分布定义为
P ( x 1 , x 2 , x 3 , x 4 , x 5 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ∣ x 1 ) P ( x 4 ∣ x 1 , x 2 ) P ( x 5 ∣ x 2 ) P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3|x_1)P(x_4|x_1,x_2)P(x_5|x_2) P(x1,x2,x3,x4,x5)=P(x1)P(x2)P(x3∣x1)P(x4∣x1,x2)P(x5∣x2)
显然, x 3 x_3 x3和 x 4 x_4 x4在给定 x 1 x_1 x1的取值时独立, x 4 x_4 x4和 x 5 x_5 x5在给定 x 2 x_2 x2的取值时独立,

为了分析有向图中变量间的条件独立性,可使用“有向分离”
先把有向图转变为一个无向图
- 找出有向图中所有 V V V型结构,在 V V V型结构两个父结点之间加一条无向边
- 将所有有向边设为无向边
由此产生的无向图称为“道德图”,令父结点相连的过程称为“道德化”

7.5.2学习
贝叶斯网学习的首要任务就是根据训练数据集来找出结构最“恰当”的贝叶斯网
“评分搜索” 先定义一个评分函数,以此来评估贝叶斯网与训练数据的契合程度,基于评分函数在寻找结构最优的贝叶斯网
“最小描述长度” MDL准则
每个贝叶斯网描述了一个在训练数据上的概率分布,自有一套编码机制能使那些经常出现的样本有更短的编码。选择综合长度最短的网。
给定训练集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1,x2,...,xm},贝叶斯网 B = < G , θ > B=<G,\theta> B=<G,θ>在 D D D上的评分函数:
s ( B ∣ D ) = f ( θ ) ∣ B ∣ − L L ( B ∣ D ) \begin{equation} s(B|D)=f(\theta)|B|-LL(B|D) \tag{7.28} \end{equation} s(B∣D)=f(θ)∣B∣−LL(B∣D)(7.28)
其中 ∣ B ∣ |B| ∣B∣是贝叶斯网的参数个数; f ( θ ) f(\theta) f(θ)表示描述每个参数 θ \theta θ所需的字节数;
L L ( B ∣ D ) = ∑ i = 1 m l o g P B ( x i ) \begin{equation} LL(B|D)=\sum_{i=1}^{m}logP_B(x_i) \tag{7.29} \end{equation} LL(B∣D)=i=1∑mlogPB(xi)(7.29)
S ( B ∣ D ) S(B|D) S(B∣D)第1项是描述网 B B B字节数,第2项是 B B B对应概率分布 P B P_B PB的字节数
- f ( θ ) = 1 f(\theta)=1 f(θ)=1得AIC评分函数
A I C ( B ∣ D ) = ∣ B ∣ − L L ( B ∣ D ) \begin{equation} AIC(B|D)=|B|-LL(B|D) \tag{7.30} \end{equation} AIC(B∣D)=∣B∣−LL(B∣D)(7.30) - f ( θ ) = 1 2 l o g m f(\theta)=\frac{1}{2}log^m f(θ)=21logm得BIC评分函数
B I C ( B ∣ D ) = 1 2 l o g m ∣ B ∣ − L L ( B ∣ D ) \begin{equation} BIC(B|D)=\frac{1}{2}log^m|B|-LL(B|D) \tag{7.31} \end{equation} BIC(B∣D)=21logm∣B∣−LL(B∣D)(7.31) - f ( θ ) = 0 f(\theta)=0 f(θ)=0评分函数退化为负对数似然
若网 B = < G , θ > B=<G,\theta> B=<G,θ>中 G G G固定,则 S ( B ∣ D ) S(B|D) S(B∣D)第1项为常数,参数 θ x i ∣ π i \theta_{x_i|\pi_i} θxi∣πi可直接由数据集 D D D得到:
θ x i ∣ π i = P ^ D ( x i ∣ π i ) \begin{equation} \theta_{x_i|\pi_i}=\hat{P}_D(x_i|\pi_i) \tag{7.32} \end{equation} θxi∣πi=P^D(xi∣πi)(7.32)
7.6EM算法
前面训练样本都是"完整"的,实际上并不一定都是“完整”。


相关文章:

《机器学习》周志华-CH7(贝叶斯分类)
7.1贝叶斯决策论 对分类任务而言,在所有相关概率已知的理想情形下,贝叶斯决策论考虑如何基于这些概率核误判损失来选择最优的类别标记。 R ( x i ∣ x ) ∑ j 1 N λ i j P ( c j ∣ x ) \begin{equation} R(x_{i}|x)\sum_{j1}^{N}\lambda_{ij}P(c_{j}…...
【C/C++】错题记录(一)
题目一 这道题主要考查了用户对标准库函数的使用规则的理解。 选项 A,一般情况下用户调用标准库函数前不需要重新定义,该项说法错误。 选项 B,即使包含了标准库头文件及相关命名空间,也不允许用户重新定义标准库函数,…...
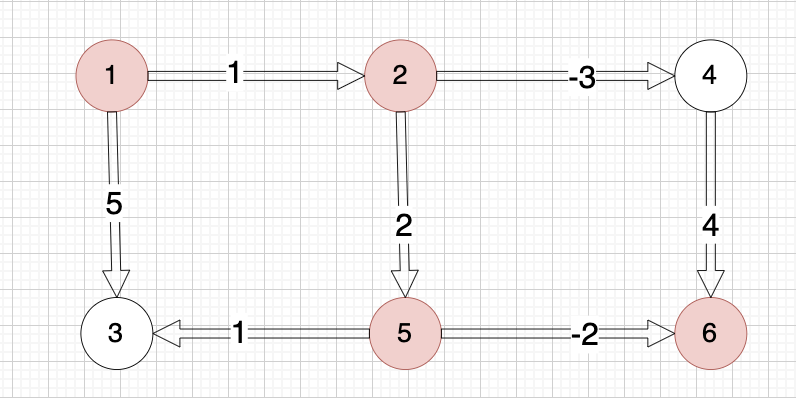
【代码随想录训练营第42期 Day60打卡 - 图论Part10 - Bellman_ford算法系列运用
目录 一、Bellman_ford算法的应用 二、题目与题解 题目一:卡码网 94. 城市间货物运输 I 题目链接 题解:队列优化Bellman-Ford算法(SPFA) 题目二:卡码网 95. 城市间货物运输 II 题目链接 题解: 队列优…...

vue复制信息到粘贴框
npm install vue-clipboard2main.js文件引入 import VueClipboard from vue-clipboard2 Vue.use(VueClipboard)页面应用 copyInfo(info){let that thislet copyData 项目名称:${info.projectName}\n 用户名:${info.username}\n 初始密码:${…...
STM32基础笔记
第一章、STM32基本介绍 总内容 计算机技术简介环境安装、项目流程搭建最小系统时钟系统启动相关:启动文件、启动流程、启动方式GPIOUSARTNVIC: 外部中断_串口中断( DMA )TIMERADCDHT11: 单总线协议SPI : LCD屏 ## **1、计算机技术简介** 1.通用计算机/专用计算机…...

【深入学习Redis丨第六篇】Redis哨兵模式与操作详解
〇、前言 哨兵是一个分布式系统,你可以在一个架构中运行多个哨兵进程,这些进程使用流言协议来接收关于Master主服务器是否下线的信息,并使用投票协议来决定是否执行自动故障迁移,以及选择哪个Slave作为新的Master。 文章目录 〇、…...

开源项目 GAN 漫画风格化 UGATIT
开源项目:DataBall / UGATIT GitCode * 数据集 * [该项目制作的训练集的数据集下载地址(百度网盘 Password: gxl1 )](https://pan.baidu.com/s/1683TRcv3r3o7jSitq3VyYA) * 预训练模型 * [预训练模型下载地址(百度网盘 Password: khbg )](https://pan.ba…...

SegFormer网络结构的学习和重构
因为太多的博客并没有深入理解,本文是自己学习后加入自己深入理解的总结记录,方便自己以后查看。 segformer中encoder、decoder的详解。 学习前言 一起来学习Segformer的原理,如果有用的话,请记得点赞关注哦。 一、Segformer的网络结构图 网络结构&…...

ubuntu个人实用配置问题
记录两年前试图用Ubuntu作为自己的日常系统的实际情况 记录时间2022年8月26日 中间连输入法都安装不上。。哈哈又被自己笑到啦! ubuntu 安装 使用市面上的各种 U 盘启动盘制作工具,下载 iso 文件之后将清空指定的 U 盘并制作为启动 U 盘,…...

Xk8s证书续期
Master节点 备份文件 cp -r /etc/kubernetes/ /etc/kubernetes-20211021-bak tar -cvzf kubernetes-20211021-bak.tar.gz /etc/kubernetes-20211021-bak/cp -r ~/.kube/ ~/.kube-20211021-bak tar -cvzf kube-20211021-bak.tar.gz ~/.kube-20211021-bakcp -r /var/lib/kube…...

仓颉编程入门2,启动HTTP服务
上一篇配置了仓颉sdk编译和运行环境,读取一个配置文件,并把配置文件简单解析了一下。 前面读取配置文件,使用File.readFrom(),这个直接把文件全部读取出来,返回一个字节数组。然后又创建一个字节流,给文件…...

Linux驱动开发初识
Linux驱动开发初识 文章目录 Linux驱动开发初识一、驱动的概念1.1 什么是驱动:1.2 驱动的分类: 二、设备的概念2.1 主设备号&次设备号:2.2 设备号的作用: 三、设备驱动整体调用过程3.1 上层用户操控设备的流程:3.2…...
)
前端面试题(三)
11. Web API 面试题 如何使用 fetch 发起网络请求? fetch 是现代浏览器中用于发起网络请求的原生 API。它返回一个 Promise,默认情况下使用 GET 请求:fetch(https://api.example.com/data).then(response > response.json()).then(data &g…...

骨传导耳机哪个牌子最好用?实测五大实用型骨传导耳机分析!
在快节奏的现代生活中,耳机已成为我们不可或缺的伴侣。无论是在通勤路上、运动时,还是在安静的图书馆,耳机都能为我们提供一片属于自己的音乐天地。然而,长时间使用传统耳机可能会对听力造成损害,尤其是在高音量下。因…...
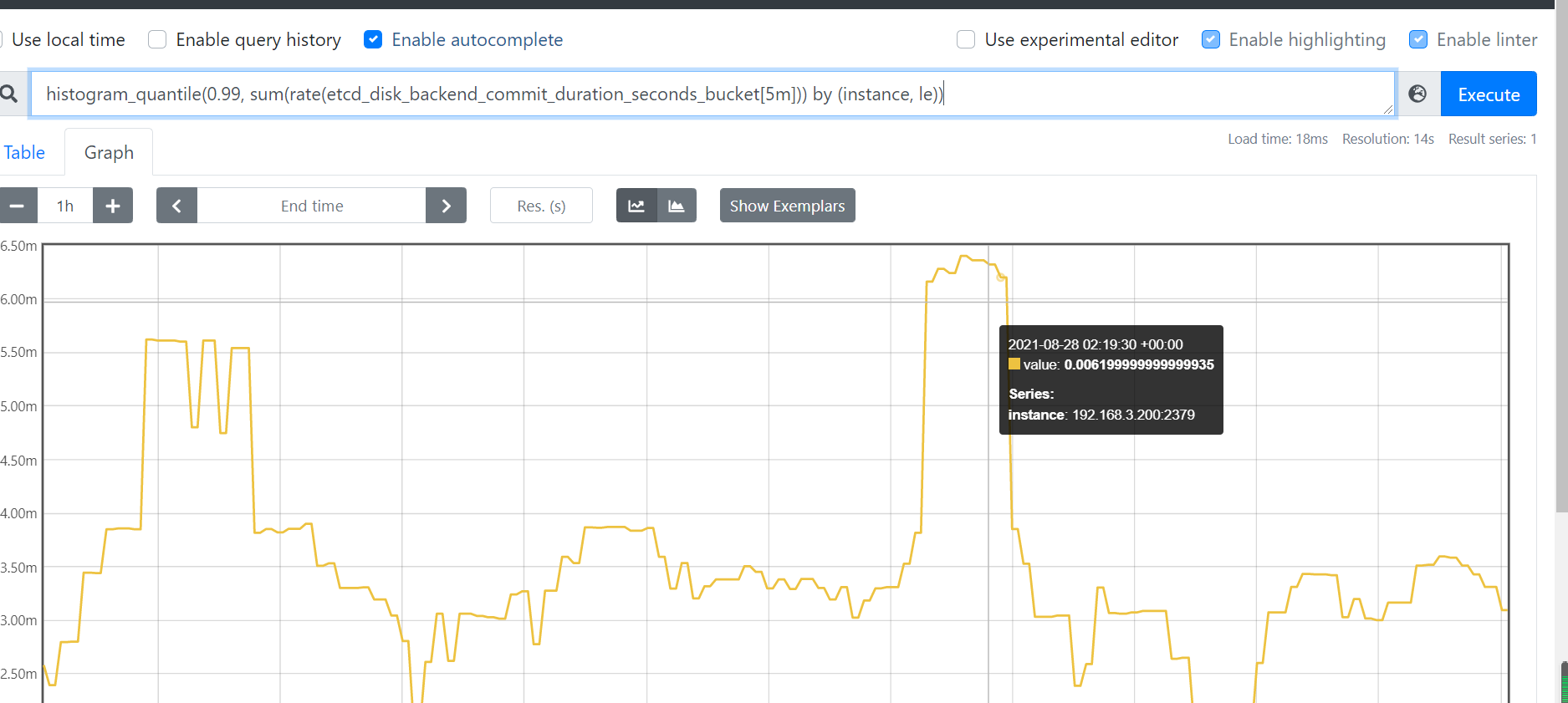
18.1 k8s服务组件之4大黄金指标讲解
本节重点介绍 : 监控4大黄金指标 Latency:延时Utilization:使用率Saturation:饱和度Errors:错误数或错误率 apiserver指标 400、500错误qps访问延迟队列深度 etcd指标kube-scheduler和kube-controller-manager 监控4大黄金指标 …...

MacOS Catalina 从源码构建Qt6.2开发库之02: 配置QtCreator
安装Qt-creator-5.0.2 在option命令中配置Qt Versions指向 /usr/local/bin/qmake6 Kits选入CLang...

某建筑市场爬虫数据采集逆向分析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 目标网站 aHR0cHM6Ly9qenNjLm1vaHVyZC5nb3YuY24vZGF0YS9jb21wYW55P2NvbXBsZXhuYW1lPSVFNiVCMCVCNA 提示:以下是本篇文章正文内容,下面…...

降低存量房贷利率的主要原因和影响
降低存量房贷利率的主要原因和影响可以从以下几个方面来分析: 原因 刺激消费与内需:降低房贷利率可以减少贷款人的月供负担,增加家庭的可支配收入,理论上能刺激消费,促进经济的内循环。在经济面临压力时,这…...

远程桌面连接工具Microsoft Remote Desktop Beta for Mac
Microsoft Remote Desktop Beta for Mac 是一款功能强大的远程桌面连接工具,具有以下功能特点: 软件下载地址 跨平台连接: 允许 Mac 用户轻松连接到运行 Windows 操作系统的计算机,打破了操作系统的界限,无论这些 Wi…...

Linux 之 logrotate 【日志分割】
简介 logrotate 是一个用于管理日志文件的工具。它可以自动对日志文件进行轮转、压缩、删除等操作,以防止日志文件无限增长占用过多磁盘空间。logrotate 通常作为一个守护进程定期运行,也可以通过 cron 任务来调度执行 工作原理 按照配置文件中的规则…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
