随想录Day43--动态规划: 1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,就把这个平均值作为背包的容量,往这里面放东西,当放的重量最接近这个背包重量时,就是最优解。dp[i][j]表示背包的重量,也就是价值,i表示第i个石头,j表示背包的容量。最后用一个res来表示背包和平均值之间的最小差值。
目标和将数组集合分成两个子集,一个表示加号,一个表示减号。利用关系add(加号中的数字和) + diff(减号的数字和) = sum(整个集合的和)以及add - diff = target,推导出add = (target + sum) / 2;不满足这个关系就说明上式不成立,也就是不能分成满足条件的两份。dp[i][j] 表示放入的方法,i表示集合中的第i个数,j表示现在背包容量,也就是add。最后的dp[nums.length ][add]就是nums集合中添加add个数的最多方法。
一和零,dp[i][j] 表示的是放入的最大子集的个数,i表示0的容量,j表示1的容量。有点像双背包,需要往这两个背包里面装东西。而加一个外循环k来挨个遍历物品strs。
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40] 输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
class Solution {public int lastStoneWeightII(int[] stones) {int len = stones.length;if(len == 1){return stones[0];}int sum = 0;for(int wight : stones){sum += wight;}int target = sum / 2 ;//这里加1个k主要是当sum是奇数时,那么最后的重量差要加上这个修正值。//比如说stones = [2,7,4,1,8,1],那么sum = 23,算出来target = 11;//如果最后背包和这个target的差值=0;那么最后剩下的重量就是1,也就是修正值//如果背包和这个target的差值=2;那么剩下的重量就是2 * 2 + 1;也就是2倍的差值加上修正值。//因为差值为2时,一个背包为9,剩下为14(13 + 1),差值就是5.int k = sum % 2;int res = sum;int[][] dp = new int [len][target + 1];for(int i = 0; i < len; i++){dp[i][0] = 0;}for(int j = 0; j <= target; j++){if(j >= stones[0]){dp[0][j] = stones[0];}}for(int i = 1; i < len; i++){for(int j = 1; j <= target; j++){if(j >= stones[i]){dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);}else{dp[i][j] = dp[i - 1][j];} }res = Math.min(res, target - dp[i][target]);}// for (int i = 0; i < len; i++) {// for (int j = 0; j <= target; j++) {// System.out.print(dp[i][j]+" ");// }// System.out.println();// }return 2 * res + k;//这是另外一种输出,也就不用计算修正值和比较背包之间差值的最小值,直接计算背包容量//装的最大的石头重量,然后剩余的重量减去背包的重量就是差值。//return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];}
}494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for(int n : nums){sum += n;}int add = 0;int diff = 0;add = (target + sum) / 2;//如果和是奇数,那肯定是不能得到合适的式子if((target + sum) % 2 != 0 || add < 0){return 0;}int [][] dp = new int[nums.length + 1][add + 1];dp[0][0] = 1;for(int i = 1; i <= nums.length; i++){for(int j = 0; j <= add; j++){if(j >= nums[i - 1]){dp[i][j] = dp[i - 1][j - nums[i - 1]] + dp[i - 1][j];}else{dp[i][j] = dp[i - 1][j];}}}return dp[nums.length ][add];}
}
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
class Solution {public int findMaxForm(String[] strs, int m, int n) {int len = strs.length;int[] zero = new int[len];int[] one = new int[len];for(int i = 0; i < len; i++){for(int j = 0; j < strs[i].length(); j++){if(strs[i].charAt(j) == '0'){zero[i] ++;}else{one[i]++;}} }int[][] dp = new int[m + 1][n + 1];for(int k = 0; k < len; k++){for(int i = m; i >= zero[k]; i--){for(int j = n; j >= one[k]; j--){dp[i][j] = Math.max(dp[i][j], dp[i - zero[k]][j - one[k]] + 1);}}}return dp[m][n];}
}相关文章:

随想录Day43--动态规划: 1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,…...

Qt中对TCP粘包的处理
当时用TCP协议传输数据时,经常出现粘包的现象 当服务器向客户端发送数据之后,客户端还没有接收数据的时候,这段时间数据在什么地方? 1、服务器?服务器已经发出数据了 2、网线?数据应该在内存,怎…...

贪心-单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9示例 2: 输入: n 1234 输出: 1234示例 3: 输入…...

你真的会用搜索引擎吗?
作为一名在校大学生,对于搜索资料这一件事深有体会,特别是在期末考试突击的时候,如何利用搜索引擎,快速找到自己想要的知识,快速理解这个知识点,想必是每位大学生的必备技能了。 我们在学习一个知识点的过…...

KDCJ-20kV冲击耐压测试仪
一、产品简介 KDCJ-20kV冲击耐压测试仪是电力设备高压试验的基本项目之一,电力设备在设计、制造及修缮之后都要求进行冲击试验以验证或检验。因此,冲击电压试验设备有着广泛的应用,在工厂、研究机构及大专院校的高压试验室中都可以看到不同规…...
【Mybatis源码分析】TypeAliasRegistry源码分析
TypeAliasRegistry源码分析一、引入类型别名二、typeAlias 的三种配置方式三、TypeAliasRegistry源码分析三种配置方式源码解析校验过程Mybatis默认的别名配置四、总结一、引入类型别名 当配置 XML 文件,需要指明Java类型时,类型别名可替代Java类型的全…...

节点高负载
如何判断节点高负载? 可以通过 top 或 uptime 来确定 load 大小,如果 load 小于 CPU 数量,属于低负载,如果大于 CPU 数量 2~3 倍,就比较高了,当然也看业务敏感程度,不太敏感的大于 4 倍算高负载。 排查思路 观察监控:通常不是因为内核 bug 导致的高负载,在卡死之前…...
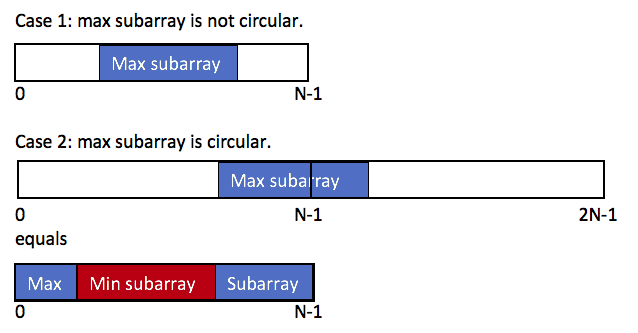
动态规划(一) part1
T1:一个数组 中的最长 升序 子序列 的长度 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组…...
Ubuntu显卡报错:Failed to initialize NVML Driver/library version mismatch
问题描述 输入指令nvidia-smi的时候,出现如下: Failed to initialize NVML: Driver/library version mismatch看起来好像是版本不匹配,在网上查了很多都没有解决问题,重启也不行,结果证明最好的办法是重新安装cuda。…...

JAVA企业电子采购系统源码:采购过程更规范,更透明
满足采购业务全程数字化, 实现供应商管理、采购需求、全网寻源、全网比价、电子招 投标、合同订单执行的全过程管理。 电子招标采购,是指在网上寻源和采购产品和服务的过程。对于企业和企业主来说,这是个既省钱又能提高供应链效率的有效方法…...
5.5G产业再提速!高通5GAdvanced-ready芯片商用终端下半年面世
MWC2023大会召开在即,5GAdvanced产业再添重磅消息!2月15日,高通宣布推出全球首个5GAdvanced-ready基带芯片——骁龙X755G调制解调器及射频系统,支持毫米波和Sub-6GHz频段,带来网络覆盖、时延、能效和移动性等全方位的提…...

基于B站王阿华的视频——为什么当下自媒体都在制造焦虑以及如何摆脱
观后笔记2.0——一些深入的思考 1.情绪大约在两千万年前,哺乳脑统治期间诞生。 2.情绪分为积极情绪和负面情绪。决定某种情绪的出现取决于安全感等级。 自媒体制造负面情绪,想尽办法挑起情绪,吸引流量 安全感充足时,由积极情绪…...
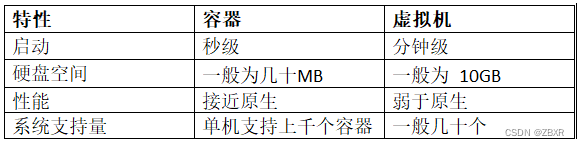
一、Docker介绍:
Docker官方网站:https://www.docker.com/ Docker容器技术是虚拟化技术的一个分支,虚拟化技术一般分为两种: 硬件级虚拟化(hardware-level-virtualization) :是运行在硬件之上的虚拟化技术,它的核…...
)
Vue进阶(一篇进入Vue3的世界)
文章目录一、初识Vue3二、Vue3新语法糖setup三、响应式数据函数3.1 ref函数3.2 reactive函数3.3 ref和reactive函数的异同四、Vue3的响应式原理五、语法更新5.1 Vue3使用computed计算属性5.2 Vue3使用watch监视属性的注意点5.2.1 监视ref对象5.2.2 监视reactive对象5.2.3 监视嵌…...

功能测试的分类,分别有什么作用?
目录 前言 一、链接测试 二、表单测试 三、搜索测试 四、删除测试 五、cookies/session测试 六、数据库测试 七、峰值测试/容量测试 八、相容性测试/安全测试 前言 功能测试主要包括链接测试、表单测试、搜索测试、删除测试、cookies、session测试、数据库测试等部分…...

51单片机学习笔记_14 红外遥控
红外传感器 遥控器通过红外 LED 发送调制后的信号,开发板上的红外接收模块接收遥控器的红外线。 单工异步,940nm 波长(还有一种 250nm 的N,可见光),EC 通信标准。 38KHz:红外线频率。 IN&…...

【我是土堆 - Pytorch教程】 知识点 学习总结笔记(五)
此文章为【我是土堆 - Pytorch教程】 知识点 学习总结笔记(五)包括:完整的模型训练套路(一)、完整的模型训练套路(二)、完整的模型训练套路(三)、利用GPU训练(…...

JUC篇:CopyOnWriteArrayList的应用与原理
系列文章目录 JUC篇:volatile可见性的实现原理 JUC篇:synchronized的应用和实现原理 JUC篇:用Java实现一个简单的线程池 JUC篇:java中的线程池 JUC篇:ThreadLocal的应用与原理 JUC篇:Java中的并发工具类 文…...
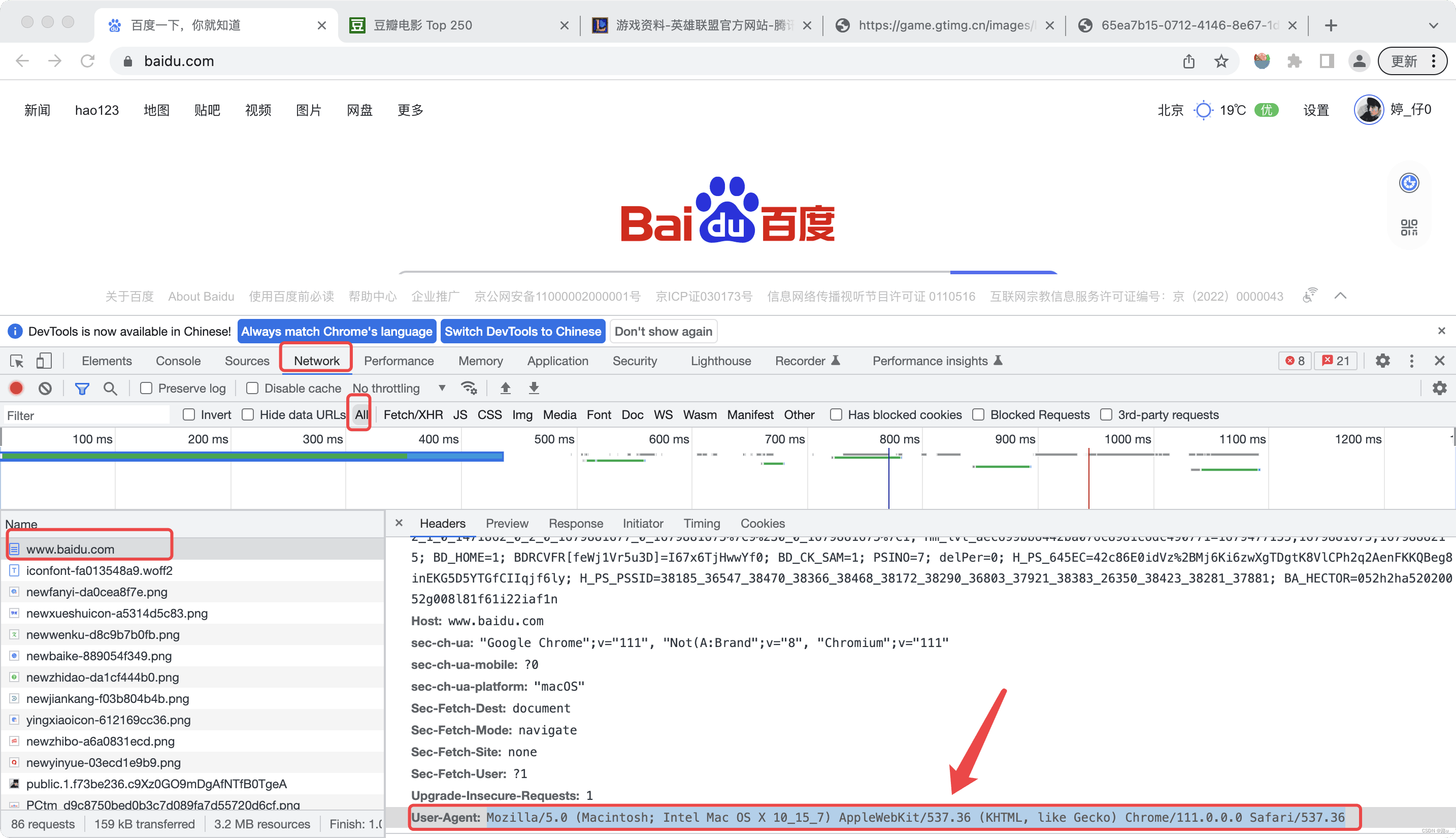
【总结】爬虫1-requests
爬虫1-requests 1. requests的基本用法 requests需要提前导入,才能使用 1.1 请求网络数据:requests.get(请求地址) response requests.get(https://cd.zu.ke.com/zufang)1.2 设置解码方法(罗马的是需要设置 - 一定要在获取请求结果之前设…...
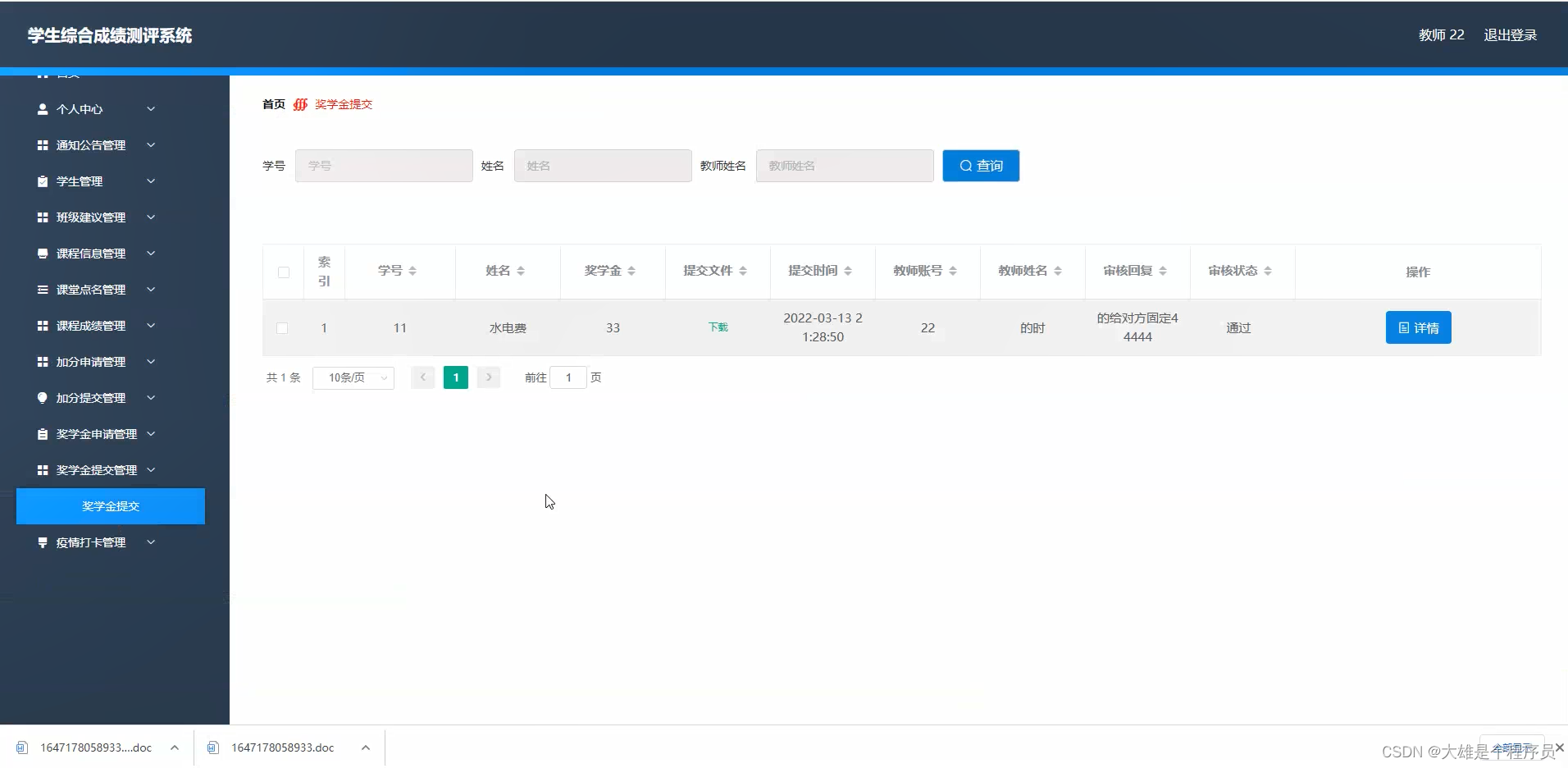
基于springboot实现学生综合成绩测评系统【源码】分享
基于springboot实现学生综合成绩测评系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
