Python 实现图形学几何变换算法
目录
- Python 实现图形学几何变换算法
- 几何变换介绍
- 变换矩阵
- Python 实现几何变换
- 代码解释
- 总结
Python 实现图形学几何变换算法
在计算机图形学中,几何变换是非常重要的概念。它们允许我们对对象的位置、大小、方向进行操作,比如平移、缩放、旋转、反射等。本文将详细介绍这些几何变换,并使用 Python 结合面向对象编程 (OOP) 的思想进行实现。
几何变换介绍
常见的几何变换包括:
- 平移 (Translation):在平面中移动对象。
- 缩放 (Scaling):根据某个比例改变对象的大小。
- 旋转 (Rotation):围绕某个点对对象进行旋转。
- 反射 (Reflection):沿某条轴对对象进行对称反射。
- 错切 (Shear):改变对象的形状但保持其体积不变。
这些几何变换都可以通过矩阵运算来描述,并应用于2D图形中的点和向量。
变换矩阵
在二维平面上,变换矩阵可以表示为 3x3 的齐次坐标矩阵。一般的二维变换可以使用下列矩阵表示:
-
平移矩阵:
T = [ 1 0 t x 0 1 t y 0 0 1 ] T = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} T= 100010txty1
其中, t x t_x tx 和 t y t_y ty 分别是沿 x 和 y 方向的平移距离。 -
缩放矩阵:
S = [ s x 0 0 0 s y 0 0 0 1 ] S = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} S= sx000sy0001
其中, s x s_x sx 和 s y s_y sy 分别是 x 和 y 方向的缩放因子。 -
旋转矩阵(绕原点逆时针旋转):
R = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] R = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} R= cosθsinθ0−sinθcosθ0001
其中, θ \theta θ 是旋转角度。 -
反射矩阵(关于 x 轴或 y 轴):
- 关于 x 轴反射:
F x = [ 1 0 0 0 − 1 0 0 0 1 ] F_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} Fx= 1000−10001 - 关于 y 轴反射:
F y = [ − 1 0 0 0 1 0 0 0 1 ] F_y = \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} Fy= −100010001
- 关于 x 轴反射:
-
错切矩阵:
H = [ 1 k x 0 k y 1 0 0 0 1 ] H = \begin{bmatrix} 1 & k_x & 0 \\ k_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} H= 1ky0kx10001
其中, k x k_x kx 和 k y k_y ky 分别是 x 和 y 方向的错切因子。
Python 实现几何变换
我们将使用 Python 的面向对象编程思想来实现几何变换类,这样可以更加灵活和可扩展。
import numpy as np# 定义二维点类
class Point2D:def __init__(self, x, y):self.x = xself.y = ydef to_homogeneous(self):"""将点转化为齐次坐标形式"""return np.array([self.x, self.y, 1])def update_from_homogeneous(self, coords):"""从齐次坐标更新点的坐标"""self.x, self.y = coords[0], coords[1]# 定义几何变换基类
class Transformation2D:def __init__(self):self.matrix = np.eye(3) # 初始化为单位矩阵def apply(self, point):"""将变换应用到一个点上"""homogeneous_point = point.to_homogeneous()transformed_point = self.matrix.dot(homogeneous_point)point.update_from_homogeneous(transformed_point)# 定义平移变换类
class Translation(Transformation2D):def __init__(self, tx, ty):super().__init__()self.matrix = np.array([[1, 0, tx],[0, 1, ty],[0, 0, 1]])# 定义缩放变换类
class Scaling(Transformation2D):def __init__(self, sx, sy):super().__init__()self.matrix = np.array([[sx, 0, 0],[0, sy, 0],[0, 0, 1]])# 定义旋转变换类
class Rotation(Transformation2D):def __init__(self, theta):super().__init__()cos_theta = np.cos(np.radians(theta))sin_theta = np.sin(np.radians(theta))self.matrix = np.array([[cos_theta, -sin_theta, 0],[sin_theta, cos_theta, 0],[0, 0, 1]])# 定义反射变换类
class Reflection(Transformation2D):def __init__(self, axis):super().__init__()if axis == 'x':self.matrix = np.array([[1, 0, 0],[0, -1, 0],[0, 0, 1]])elif axis == 'y':self.matrix = np.array([[-1, 0, 0],[0, 1, 0],[0, 0, 1]])# 定义错切变换类
class Shear(Transformation2D):def __init__(self, kx, ky):super().__init__()self.matrix = np.array([[1, kx, 0],[ky, 1, 0],[0, 0, 1]])# 使用示例
if __name__ == "__main__":# 创建一个二维点point = Point2D(1, 1)# 平移变换translation = Translation(2, 3)translation.apply(point)print(f"After translation: ({point.x}, {point.y})")# 缩放变换scaling = Scaling(2, 2)scaling.apply(point)print(f"After scaling: ({point.x}, {point.y})")# 旋转变换rotation = Rotation(90)rotation.apply(point)print(f"After rotation: ({point.x}, {point.y})")# 反射变换reflection = Reflection('x')reflection.apply(point)print(f"After reflection: ({point.x}, {point.y})")# 错切变换shear = Shear(1, 0)shear.apply(point)print(f"After shear: ({point.x}, {point.y})")
代码解释
-
Point2D类:表示一个二维点。该类提供了将点转化为齐次坐标形式的方法,并能从变换后的齐次坐标更新点的坐标。
-
Transformation2D基类:几何变换的基类,定义了变换矩阵(初始为单位矩阵),并且定义了
apply方法,用于将变换矩阵作用到一个点上。 -
具体的几何变换类:如
Translation、Scaling、Rotation、Reflection和Shear类,都继承自Transformation2D,并分别实现自己的变换矩阵。 -
使用示例:创建一个二维点,并依次应用平移、缩放、旋转、反射、错切等变换。
总结
通过面向对象的思想实现几何变换,可以使得代码结构更加清晰且易于扩展。每种变换都可以作为一个独立的类来实现,同时也可以轻松添加新的变换类型。通过这种方式,我们能够灵活地对二维图形进行复杂的变换操作。
希望这篇文章能帮助你更好地理解几何变换及其在图形学中的应用。如果有任何问题或建议,欢迎交流!
相关文章:

Python 实现图形学几何变换算法
目录 Python 实现图形学几何变换算法几何变换介绍变换矩阵Python 实现几何变换代码解释总结 Python 实现图形学几何变换算法 在计算机图形学中,几何变换是非常重要的概念。它们允许我们对对象的位置、大小、方向进行操作,比如平移、缩放、旋转、反射等。…...

接口测试|超详细面试题【附答案】
今天给姐妹们整理了一套超详细的附答案的接口测试面试题,姐妹们快学起来吧~ 接口测试的重要性,相信不用我多说了。接口测试是现在软件测试工程师一个加分项。因为很多朋友一开始做了几年的软件测试都是在做功能测试,做界面UI的测试ÿ…...

Qt网络编程——QTcpServer和QTcpSocket
文章目录 核心APITCP回显服务器TCP回显客户端 核心API QTcpServer用于监听端口和获取客户端连接 名称类型说明对标原生APIlisten(const QHostAddress&, quint16 port)方法绑定指定的地址和端口号,并开始监听bind和listennextPendingConnection()方法从系统中获…...

CentOS 7 aarch64制作openssh 9.9p1 rpm包 —— 筑梦之路
本篇文章还是基于开源项目openssh-rpms制作。 https://github.com/boypt/openssh-rpms.git 官方发行说明: OpenSSH: Release Notes 1. 修改version.env 2. 下载源码包 openssl网站改版,下载地址和之前不一样了 # 下载openssl1.1.1w源码包cd downlo…...

Flink和Spark的区别
1、设计理念不同 flink:Flink是基于事件驱动的,是面向流的处理框架, Flink基于每个事件一行一行地流式处理,是真正的流式计算. 另外他也可以基于流来模拟批进行计算实现批处理。 spark:Spark的技术理念是使用微批来模拟流的计算,…...

以太网开发基础-MAC和PHY
直接参考: 以太网基础-MAC和PHY-CSDN博客 路由器上一般有三类MAC地址 给一个范例: 00:0C:E5:4B:F2:85 这个地址就可以作为LAN MAC地址 00:0C:E5:4B:F2:86 这个地址就可以作为WAN MAC地址 00:0C:E5:4B:F2:87 这个地址就可以作为无线 MAC地址 通常,路由器…...

Java 发布jar包到maven中央仓库(2024年9月保姆级教程)
文章目录 前言一、账号准备1. 注册登录账号2. 新建命名空间3. 验证命名空间4. 生成令牌5. 为 maven 设置令牌二、GPG准备1. 下载GPG2. 发布证书2.1 新建证书2.2 发布证书到服务器2.3 验证发布三、发布jar包到中央仓库1. 编辑项目pom文件2. 打包上传3. 发布jar包4. 搜索我们的ja…...

Pandas和Seaborn可视化详解
1.Pandas绘图-单变量 概述 pandas库是Python数据分析的核心库 它不仅可以加载和转换数据,还可以做更多的事情:它还可以可视化 pandas绘图API简单易用,是pandas流行的重要原因之一 可视化小技巧: 如果是类别型 柱状 饼图 (类别相对较少 5-…...

【Python】Windows下安装使用FFmpeg
FFmpeg是一套可以用来记录、转换数字音频、视频,并能将其转化为流的开源计算机程序。之前为了MP3转wav,需要pip安装并import AudioSegment,但是会报错:FileNotFoundError: [WinError 2] 系统找不到指定的文件。 因为FFmpeg需要另…...

LLM - 使用 XTuner 指令微调 多模态大语言模型(InternVL2) 教程
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/142528967 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 XTuner…...

【Python】数据可视化之热力图
热力图(Heatmap)是一种通过颜色深浅来展示数据分布、密度和强度等信息的可视化图表。它通过对色块着色来反映数据特征,使用户能够直观地理解数据模式,发现规律,并作出决策。 目录 基本原理 sns.heatmap 代码实现 基…...
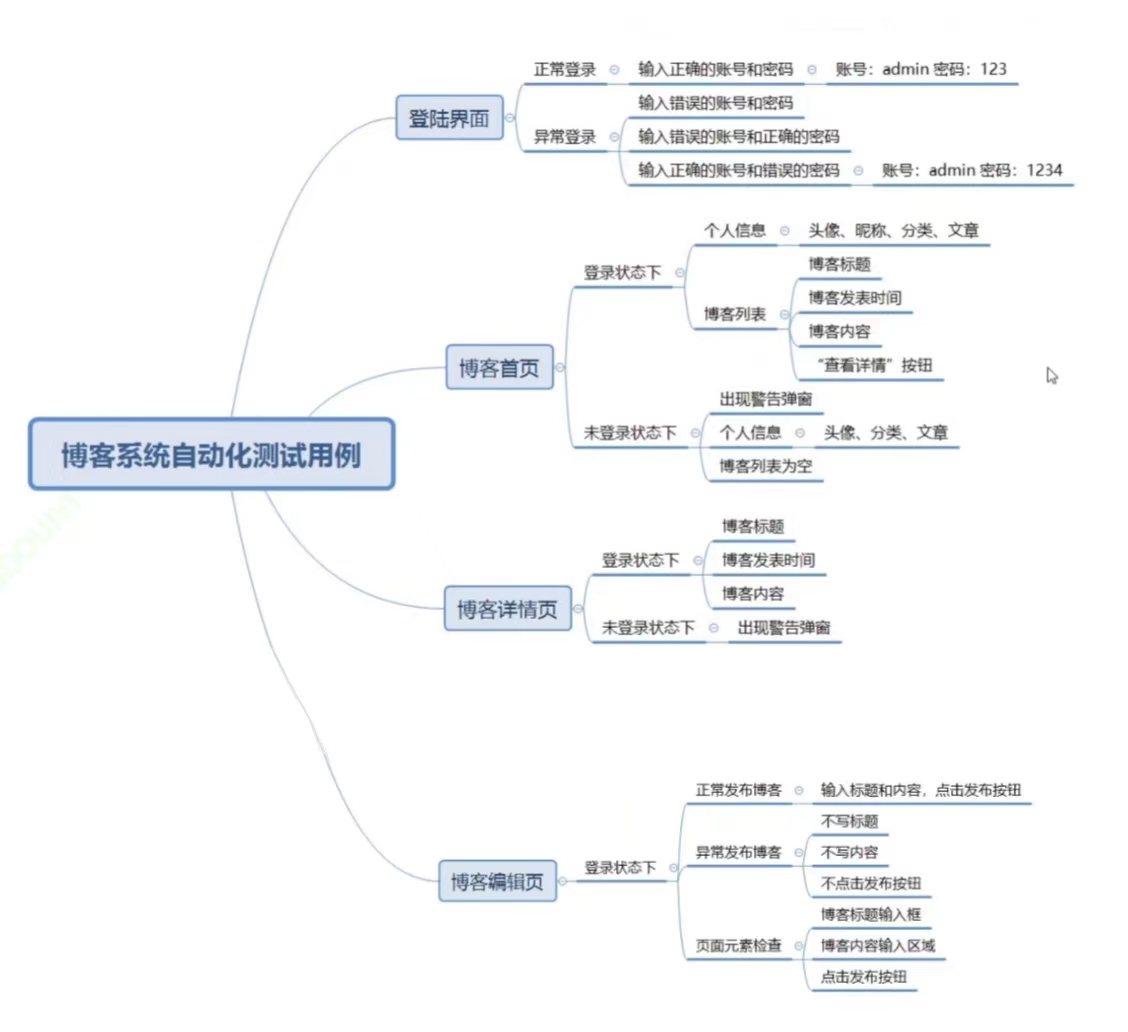
个人博客系统测试(selenium)
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 博主主页:Yan. yan. …...

【速成Redis】01 Redis简介及windows上如何安装redis
前言: 适用于:需要快速掌握redis技能的人(比如我),在b站,找了个课看。 01.课程简介_哔哩哔哩_bilibili01.课程简介是【GeekHour】一小时Redis教程的第1集视频,该合集共计19集,视频…...
和入侵预防系统(IPS))
入侵检测系统(IDS)和入侵预防系统(IPS)
入侵检测系统(IDS)和入侵预防系统(IPS)是网络安全领域中用来检测和防止潜在的恶意活动或政策违规行为的系统。它们的主要目的是保护网络和主机不受未授权访问和各种形式的攻击。以下是它们的主要区别和功能: 一&#…...

pytorch 加载模型参数后 如何测试数据,应用模型预测数据,然后连续变量转换成 list 或者numpy.array padans并保存到csv文件中
在PyTorch中,加载模型参数后测试数据通常涉及以下几个步骤: 1. **加载模型**:首先,你需要定义模型的结构,然后加载预训练的参数。 2. **加载数据**:准备你的测试数据集。确保数据集已经正确地预处理&…...
)
uni-app开发流程(开发、预览、构建和发布过程)
uni-app 是一个使用 Vue.js 开发所有前端应用的框架,支持编写一次代码,生成可以在多个平台(如微信小程序、H5、App等)运行的应用。下面是 uni-app 的开发流程,包括从创建项目到部署的各个阶段。 1. 创建项目 通过 HB…...

Linux Shell: 使用 Expect 自动化 SCP 和 SSH 连接的 Shell 脚本详解
文章目录 0. 引言2. 解决方案3. 脚本详解脚本1:使用 SSH 和 Expect 自动化登录远端机器脚本说明 脚本2:使用 SCP 和 Expect 自动化文件上传脚本说明 脚本3:使用 SCP 和 Expect 自动化文件下载脚本说明 4. 脚本的使用方法5. 关键技术点5.1. Ex…...
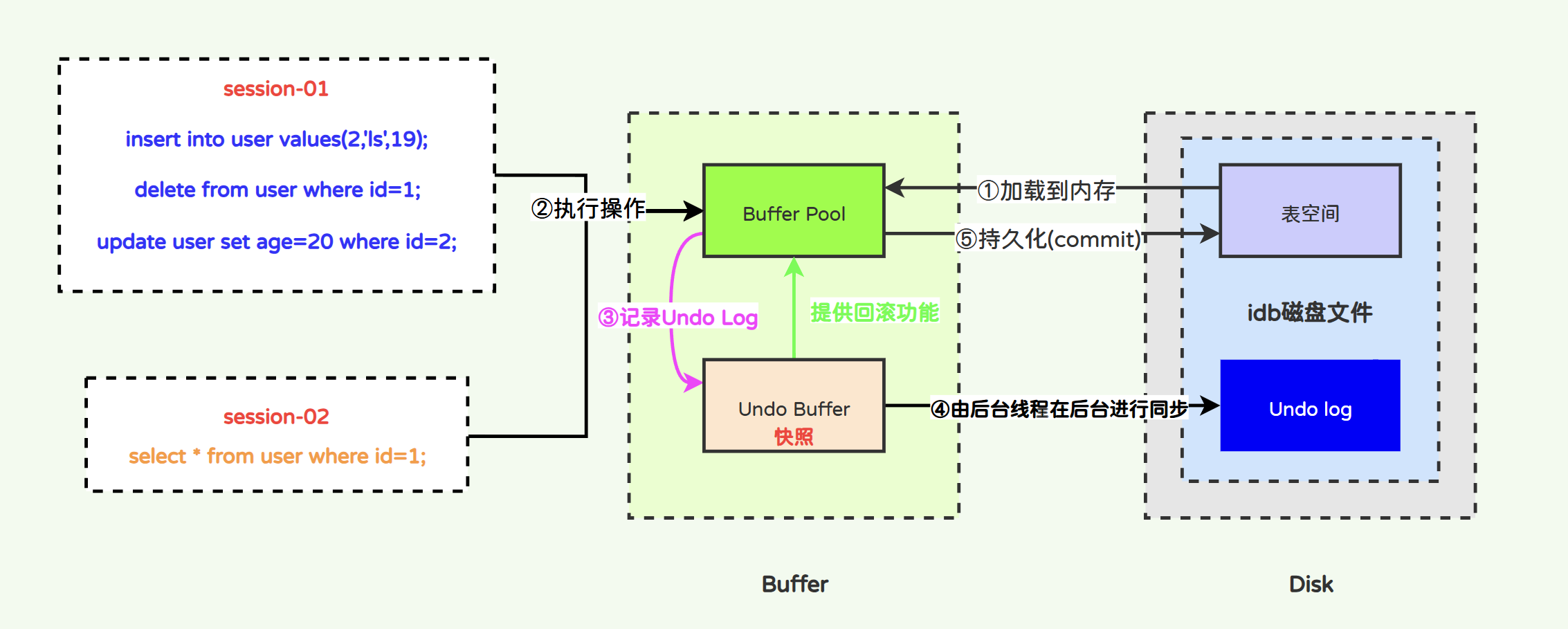
深入分析MySQL事务日志-Undo Log日志
文章目录 InnoDB事务日志-Undo Log日志2.1 Undo Log2.1.1 Undo Log与原子性2.1.2 Undo的存储格式1)insert类型Undo Log2)delete类型Undo Log3)update类型Undo Log 2.1.3 Undo Log的工作原理2.1.4 Undo Log的系统参数2.1.5 Undo Log与Purge线程…...
828华为云征文 | 在Huawei Cloud EulerOS系统中安装Docker的详细步骤与常见问题解决
前言 Docker是一种轻量级的容器技术,广泛用于应用程序的开发、部署和运维。在华为云的欧拉(Huawei Cloud EulerOS)系统上安装和运行Docker,虽然与CentOS有相似之处,但在具体实现过程中,可能会遇到一些系统…...
什么是数据增强中的插值法?
一、插值法的概念 在数据增强中,插值法是一种重要的技术,它通过数学模型在已知数据点之间估计未知数据点的值。这种方法可以帮助我们在不增加实际数据的情况下,通过生成新的数据点来扩展数据集。插值法基于这样的假设:如果已知的数…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
