1.随机事件与概率
第一章 随机时间与概率
1. 随机事件及其运算
1.1 随机现象
确定性现象:只有一个结果的现象
确定性现象:结果不止一个,且哪一个结果出现,人们事先并不知道
1.2 样本空间
样本空间:随机现象的一切可能基本结果组成的集合,记为 Ω = { ω } \Omega = \{\omega\} Ω={ω},其中 ω \omega ω表示基本结果,又称为样本点。
1.3 随机事件
随机事件:随机现象的某些基本样本点组成的集合称为随机时间,简称事件,常用大写字母 A , B , C , ⋯ A,B,C,\cdots A,B,C,⋯表示。
维恩(Venn)图:类似图1的图形

由样本空间 Ω \Omega Ω中的单个元素组成的子集称为基本事件,而样本空间 Ω \Omega Ω的最大子集(即 Ω \Omega Ω本身)称为必然事件,样本空间 Ω \Omega Ω的最小子集(即空集$\varnothing $)称为不可能事件。
1.4 随机变量
随机变量:用来表示随机现象结果的变量,常用大写字母X,Y,Z表示,很多时间都可用随机变量表示,表示时应写明随机变量的含义。
1.5 事件间的关系
包含关系:如果属于A的样本点必属于B,则称A被包含在B中,或称B包含A,记为 A ⊂ B A\subset B A⊂B
相等关系:属于A的样本点必属于B,属于B的样本点必属于A,即 A ⊂ B A\subset B A⊂B 且 B ⊂ A B\subset A B⊂A,则称事件A与B相等,记为A=B
互不相容:如果A与B没有相同的样本点,则称A与B互不相容。
2.概率的定义及其确定方法
1933年苏联数学家柯尔莫戈洛夫首次提出了概率的公理化定义。
2.1 概率的公理化定义
定义2.1 概率
设 Ω \Omega Ω为一个样本空间, F F F为 Ω \Omega Ω的某些子集组成的一个事件域,如果对于任一事件 A ∈ F A\in F A∈F,定义在 F F F上的一个实值函数 P ( A ) P(A) P(A)满足:
-
非负性公理 若 A ∈ F A\in F A∈F,则 P ( A ) ≥ 0 ; P(A)\ge 0; P(A)≥0;
-
正则性公理 P ( Ω ) = 1 P(\Omega)=1 P(Ω)=1;
-
可列可加性公理 若 A 1 , A 2 , ⋯ , A n , ⋯ A_1,A_2,\cdots,A_n,\cdots A1,A2,⋯,An,⋯互不相容,则:
P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty} A_i )=\sum_{i=1}^\infty P(A_i) P(i=1⋃∞Ai)=i=1∑∞P(Ai)
称 P ( A ) P(A) P(A)为事件 A A A的概率,称三元素 ( Ω , F , P ) (\Omega,F,P) (Ω,F,P)为概率空间。
排列和组合: p13
抽样模型 p16
放回抽样 p18
额,全看一下吧,从p12 的1.2.2 排列与组合公式开始。
3.概率的性质
性质3.1 $P(\varnothing)= 0 $
3.1 概率的可加性
性质3.2 有限可加性
若有限个时间 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An互不相容,则有
P ( ⋃ i = 1 n A i ) = ∑ i = 1 n P ( A i ) P(\bigcup_{i=1}^n A_i)=\sum_{i=1}^n P(A_i) P(i=1⋃nAi)=i=1∑nP(Ai)
性质3.3 对立事件的概率
对任意时间 A A A,有:
P ( A ‾ ) = 1 − P ( A ) P(\overline{A}) = 1- P(A) P(A)=1−P(A)
例题:甲乙抛硬币,甲抛 n + 1 n+1 n+1次,乙抛 n n n次,求甲抛出正面次数大于乙抛出正面次数的概率 P ( A ) P(A) P(A)
解:
事件A定义为 甲 正 > 乙 正 甲_正>乙_正 甲正>乙正,则 A ‾ = 甲 正 ≤ 乙 正 \overline{A}=甲_正\le 乙_正 A=甲正≤乙正
P ( A ) = P ( 甲 正 > 乙 正 ) = P ( n + 1 − 甲 反 > n − 乙 反 ) = P ( 甲 反 < 乙 反 + 1 ) = P ( 甲 反 ≤ 乙 反 ) = P ( 甲 正 ≤ 乙 正 ) = P ( A ‾ ) P(A)=P(甲_正>乙_正)=P(n+1 - 甲_反 >n - 乙_反)=P(甲_反 < 乙_反 +1)=P(甲_反\le 乙_反)=P(甲_正\le 乙_正)=P(\overline{A}) P(A)=P(甲正>乙正)=P(n+1−甲反>n−乙反)=P(甲反<乙反+1)=P(甲反≤乙反)=P(甲正≤乙正)=P(A)
则 P ( A ) = P ( A ‾ ) = 1 2 P(A)=P(\overline{A})=\frac 12 P(A)=P(A)=21
3.2 概率的单调性
性质 3.4 包含关系的性质
若 B ⊂ A B\subset A B⊂A,则
P ( A − B ) = P ( A ) − P ( B ) P(A-B) = P(A)-P(B) P(A−B)=P(A)−P(B)
推论(单调性) 若 B ⊂ A B\subset A B⊂A ,则 P ( A ) ≥ P ( B ) P(A)\ge P(B) P(A)≥P(B)
性质3.5 概率差 p30
对任意两个事件 A , B A,B A,B,有
P ( A − B ) = P ( A ) − P ( A B ) P(A-B) = P(A)-P(AB) P(A−B)=P(A)−P(AB)
3.3 概率的加法公式
性质3.6 加法公式 p31
对任意两个事件 A , B A,B A,B有
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(A\cup B) = P(A)+P(B)-P(AB) P(A∪B)=P(A)+P(B)−P(AB)
对任意n个时间 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,有:
P ( ⋃ i = 1 n A i ) = ∑ i = 1 n P ( A − i ) − ∑ 1 ≤ i < j ≤ n P ( A i A j ) + ∑ 1 ≤ i < j < k ≤ n P ( A i A j A k ) + ⋯ + ( − 1 ) n − 1 P ( A 1 A 2 ⋯ A n ) P(\bigcup_{i=1}^n A_i) =\sum_{i=1}^n P(A-i) - \sum_{1\le i<j \le n}P(A_iA_j) +\sum_{1\le i < j <k\le n}P(A_iA_jA_k)+\cdots+(-1)^{n-1}P(A_1A_2\cdots A_n) P(i=1⋃nAi)=i=1∑nP(A−i)−1≤i<j≤n∑P(AiAj)+1≤i<j<k≤n∑P(AiAjAk)+⋯+(−1)n−1P(A1A2⋯An)
推论(半可加性) 对任意两个事件 A , B A,B A,B,有
P ( A ∪ B ) ≤ P ( A ) + P ( B ) P(A\cup B)\le P(A)+P(B) P(A∪B)≤P(A)+P(B)
对任意 n n n个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An有
P ( ⋃ i = 1 n A i ) ≤ ∑ i = 1 n P ( A i ) P(\bigcup_{i=1}^n A_i) \le \sum_{i=1}^n P(A_i) P(i=1⋃nAi)≤i=1∑nP(Ai)
p32 的配对问题,很重要
3.4 概率的连续性
定义3.1 极限事件
-
对 F F F中任一单调不减的事件序列 F 1 ⊂ F 2 ⊂ ⋯ ⊂ F n ⊂ ⋯ F_1\subset F_2 \subset\cdots \subset F_n \subset \cdots F1⊂F2⊂⋯⊂Fn⊂⋯,称可列并 ⋃ n = 1 ∞ F n \bigcup_{n=1}^\infty F_n ⋃n=1∞Fn为 { F n } \{F_n\} {Fn}的极限事件,记为
l i m n → ∞ F n = ⋃ n = 1 ∞ F n lim_{n\rightarrow \infty}F_n = \bigcup_{n=1}^\infty F_n limn→∞Fn=n=1⋃∞Fn -
对 F F F中任一单调不增的事件序列 E 1 ⊃ E 2 ⊃ ⋯ ⊃ E n ⊃ ⋯ E_1\supset E_2 \supset\cdots \supset E_n \supset \cdots E1⊃E2⊃⋯⊃En⊃⋯,称可列并 ⋂ n = 1 ∞ E n \bigcap_{n=1}^\infty E_n ⋂n=1∞En为 { E n } \{E_n\} {En}的极限事件,记为
l i m n → ∞ E n = ⋂ n = 1 ∞ E n lim_{n\rightarrow \infty}E_n = \bigcap_{n=1}^\infty E_n limn→∞En=n=1⋂∞En
定义3.2 连续,上连续,下连续
对F上的一个概率P
-
若它对F中任一单调不减的事件序列 { F n } \{F_n\} {Fn}均成立
l i m n → ∞ P ( F n ) = P ( l i m n → ∞ F n ) lim_{n\rightarrow \infty} P(F_n) = P(lim_{n\rightarrow \infty}F_n) limn→∞P(Fn)=P(limn→∞Fn)
则称概率 P P P是下连续的,(左连续,P从小变大) -
若它对F中任一单调不增的事件序列 { E n } \{E_n\} {En}均成立
l i m n → ∞ P ( E n ) = P ( l i m n → ∞ E n ) lim_{n\rightarrow \infty} P(E_n) = P(lim_{n\rightarrow \infty}E_n) limn→∞P(En)=P(limn→∞En)
则称概率 P P P是上连续的,(右连续,P从大变小)
性质3.7 概率的连续性 p33
若P为事件域F上的概率,则P既是下连续的,又是上连续的。
性质3.8 可列可加性的条件 p34
若P是F上满足 P ( Ω ) = 1 P(\Omega) = 1 P(Ω)=1的非负集合函数,则它具有可列可加性的充要条件是:
- 它是有限可加的
- 它是下连续的
4.条件概率
4.1条件概率的定义 p37
定义4.1 条件概率
设A与B是样本空间 Ω \Omega Ω中的两事件,若$P(B)\gt 0 $,则称:
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
为在B发生下A的条件概率,简称条件概率
性质4.1 条件概率的性质
条件概率是概率,即若设 P ( B ) > 0 P(B)\gt 0 P(B)>0,则:
- P ( A ∣ B ) ≥ 0 , A ∈ F P(A|B)\ge 0,A\in F P(A∣B)≥0,A∈F
- P ( Ω ∣ B ) = 1 P(\Omega|B) = 1 P(Ω∣B)=1
- 若F中的 A 1 , A 2 , ⋯ , A n , ⋯ A_1,A_2,\cdots,A_n,\cdots A1,A2,⋯,An,⋯互不相容,则
P ( ⋃ n = 1 ∞ A n ∣ B ) = ∑ n − 1 ∞ P ( A n ∣ B ) P(\bigcup_{n=1}^\infty A_n |B) =\sum_{n-1}^\infty P(A_n|B) P(n=1⋃∞An∣B)=n−1∑∞P(An∣B)
4.2 乘法公式
-
若 P ( B ) > 0 P(B)\gt 0 P(B)>0,则
P ( A B ) = P ( B ) P ( A ∣ B ) P(AB) = P(B)P(A|B) P(AB)=P(B)P(A∣B) -
若 P ( A 1 A 2 ⋯ A n − 1 ) > 0 P(A_1A_2\cdots A_{n-1})\gt 0 P(A1A2⋯An−1)>0,则
P ( A 1 A 2 ⋯ A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) ⋯ P ( A n ∣ A 1 A 2 ⋯ A n − 1 ) P(A_1A_2\cdots A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1A_2\cdots A_{n-1}) P(A1A2⋯An)=P(A1)P(A2∣A1)P(A3∣A1A2)⋯P(An∣A1A2⋯An−1)
罐子模型 p39
4.3 全概率公式 p40
设 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn为样本空间 Ω \Omega Ω的一个分割,即 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn互不相容,且 ⋃ i = 1 n B i = Ω \bigcup_{i=1}^n B_i=\Omega ⋃i=1nBi=Ω,如果 P ( B i ) > 0 , i = 1 , 2 , ⋯ , n P(B_i)\gt 0,i=1,2,\cdots,n P(Bi)>0,i=1,2,⋯,n,则对任一事件有:
P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A) =\sum_{i=1}^n P(B_i)P(A|B_i) P(A)=i=1∑nP(Bi)P(A∣Bi)
4.4 贝叶斯公式 p43
设 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn是样本空间 Ω \Omega Ω的一个分割,即 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn互不相容,且 ⋃ i = 1 n B i = Ω \bigcup_{i=1} ^n B_i = \Omega ⋃i=1nBi=Ω,如果 P ( A ) > 0 , P ( B i ) > 0 , i = 1 , 2 , ⋯ , n P(A)>0,P(B_i)>0,i=1,2,\cdots,n P(A)>0,P(Bi)>0,i=1,2,⋯,n,则
P ( B i ∣ A ) = P ( A B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( B j ) P ( A ∣ B j ) , i = 1 , 2 , ⋯ , n P(B_i|A)=\cfrac{P(AB_i)}{P(A)}=\cfrac{P(B_i)P(A|B_i)}{\sum_{j=1}^{n}P(B_j)P(A|B_j)},i=1,2,\cdots,n P(Bi∣A)=P(A)P(ABi)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi),i=1,2,⋯,n
分子用乘法公式,分母用全概率公式
贝叶斯分类器 p43
肝癌的例子p43
5.独立性
5.1 两个事件的独立性
独立性:一个事件的发生不影响另一个事件的发生:
P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
若 P ( A ) = 0 ∣ ∣ P ( B ) = 0 P(A)=0||P(B)=0 P(A)=0∣∣P(B)=0,等式依然成立。
定义5.1 独立
如果 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B),则称 A A A与 B B B相互独立,简称 A A A与 B B B独立,否则成不独立或相依
独立的性质
若事件 A A A与 B B B独立,则 A A A与 B ‾ \overline{B} B独立, A ‾ \overline{A} A与 B B B独立, A ‾ \overline{A} A与 B ‾ \overline{B} B独立
证明:P48,由补的性质可以推出
5.2 多个事件的相互独立性
定义 5.2 三个事件的独立
设 A , B , C A,B,C A,B,C是三个事件,如果有:
{ P ( A B ) = P ( A ) P ( B ) P ( A B ) = P ( A ) P ( C ) P ( A B ) = P ( B ) P ( C ) \left\{ \begin{aligned} P(AB) & = P(A)P(B)\\ P(AB) & = P(A)P(C)\\ P(AB) & = P(B)P(C) \end{aligned} \right. ⎩ ⎨ ⎧P(AB)P(AB)P(AB)=P(A)P(B)=P(A)P(C)=P(B)P(C)
则称 A , B , C A,B,C A,B,C两两独立,若还有:
P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC) = P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C)
则称 A , B , C A,B,C A,B,C相互独立
定义 5.3 相互独立
设有 n n n个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,对任意的 1 ≤ i < j < k < ⋯ ≤ n 1\le i \lt j \lt k \lt \cdots \le n 1≤i<j<k<⋯≤n,如果以下等式均成立:
{ P ( A i A j ) = P ( A i ) P ( A j ) , P ( A i A j A k ) = P ( A i ) P ( A j ) P ( A k ) , ⋯ ⋯ ⋯ P ( A 1 A 2 ⋯ A n ) = P ( A 1 ) P ( A 2 ) ⋯ P ( A n ) , \left\{ \begin{aligned} P(A_i A_j) & =P(A_i)P(A_j),\\ P(A_i A_j A_k) & =P(A_i)P(A_j)P(A_k),\\ &\cdots\cdots\cdots\\ P(A_1 A_2\cdots A_n) & =P(A_1)P(A_2)\cdots P(A_n), \end{aligned} \right. ⎩ ⎨ ⎧P(AiAj)P(AiAjAk)P(A1A2⋯An)=P(Ai)P(Aj),=P(Ai)P(Aj)P(Ak),⋯⋯⋯=P(A1)P(A2)⋯P(An),
则称这 n n n个事件相互独立
例1.5.5 p50 ,甲乙比赛射击
例1.5.6 p51 ,桥式电路
5.3 试验的独立性
利用事件的独立性可以定义两个或更多个试验的独立性
定义5.4 试验相互独立
设有两个试验 E 1 E_1 E1和 E 2 E_2 E2,假如试验 E 1 E_1 E1的任一结果(事件)与试验 E 2 E_2 E2的任一结果(事件)都是相互独立的事件,则称这两个试验相互独立
类似的可推广定义到n个试验,如果n个试验的任一结果都是相互独立的事件,则称这n个试验相互独立,如果这 n n n个独立试验还是相同的,则称其为n重独立重复试验,如果在 n n n重独立重复试验中,每次试验的可能结果为两个: A A A或 A ‾ \overline{A} A,则称这种试验为n重伯努利(Bernoulli)试验。
相关文章:

1.随机事件与概率
第一章 随机时间与概率 1. 随机事件及其运算 1.1 随机现象 确定性现象:只有一个结果的现象 确定性现象:结果不止一个,且哪一个结果出现,人们事先并不知道 1.2 样本空间 样本空间:随机现象的一切可能基本…...

Redis结合Caffeine实现二级缓存:提高应用程序性能
本文将详细介绍如何使用CacheFrontend和Caffeine来实现二级缓存。 1. 简介 CacheFrontend: 是一种用于缓存的前端组件或服务。通俗的讲:该接口可以实现本地缓存与redis自动同步,如果本地缓存(JVM级)有数据,则直接从本…...

【LLM】Ollama:本地大模型 WebAPI 调用
Ollama 快速部署 安装 Docker:从 Docker 官网 下载并安装。 部署 Ollama: 使用以下命令进行部署: docker run -d -p 11434:11434 --name ollama --restart always ollama/ollama:latest进入容器并下载 qwen2.5:0.5b 模型: 进入 O…...
Excel监听以及常用工具类)
SpringBoot集成阿里easyexcel(二)Excel监听以及常用工具类
EasyExcel中非常重要的AnalysisEventListener类使用,继承该类并重写invoke、doAfterAllAnalysed,必要时重写onException方法。 Listener 中方法的执行顺序 首先先执行 invokeHeadMap() 读取表头,每一行都读完后,执行 invoke()方法…...

使用ELK Stack进行日志管理和分析:从入门到精通
在现代IT运维中,日志管理和分析是确保系统稳定性和性能的关键环节。ELK Stack(Elasticsearch, Logstash, Kibana)是一个强大的开源工具集,广泛用于日志收集、存储、分析和可视化。本文将详细介绍如何使用ELK Stack进行日志管理和分…...

前端框架对比与选择
🤖 作者简介:水煮白菜王 ,一位资深前端劝退师 👻 👀 文章专栏: 前端专栏 ,记录一下平时在博客写作中,总结出的一些开发技巧✍。 感谢支持💕💕💕 目…...
Springboot jPA+thymeleaf实现增删改查
项目结构 pom文件 配置相关依赖: 2.thymeleaf有点类似于jstlel th:href"{url}表示这是一个链接 th:each"user : ${users}"相当于foreach,对user进行循环遍历 th:if进行if条件判断 {变量} 与 ${变量}的区别: 4.配置好application.ym…...
【YashanDB知识库】yashandb执行包含带oracle dblink表的sql时性能差
本文内容来自YashanDB官网,具体内容请见https://www.yashandb.com/newsinfo/7396959.html?templateId1718516 问题现象 yashandb执行带oracle dblink表的sql性能差: 同样的语句,同样的数据,oracle通过dblink访问远端oracle执行…...

效率工具推荐 | 高效管理客服中心知识库
人工智能AI的广泛应用,令AI知识库管理已成为优化客服中心运营的核心策略之一。一个高效、易用且持续更新的知识库不仅能显著提升客服代表的工作效率,还能极大提升客户的服务体验。而高效效率工具如HelpLook,能够轻松搭建AI客服帮助中心&#…...
综合实验1 利用OpenCV统计物体数量
一、实验简介 传统的计数方法常依赖于人眼目视计数,不仅计数效率低,且容易计数错误。通常现实中的对象不会完美地分开,需要通过进一步的图像处理将对象分开并计数。本实验巩固对OpenCV的基础操作的使用,适当的增加OpenCV在图像处…...
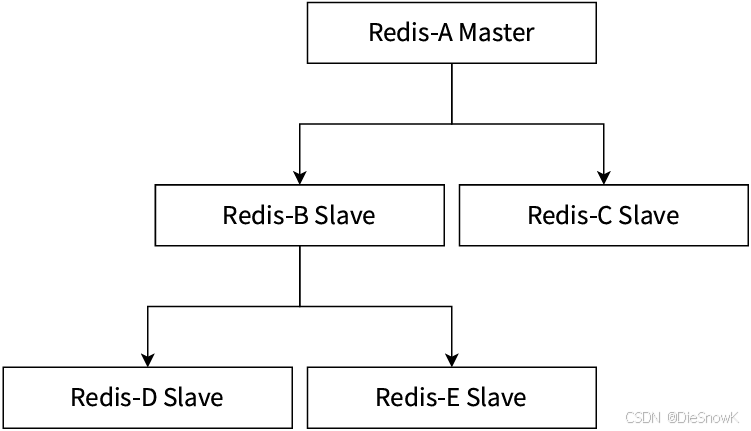
[Redis][主从复制][上]详细讲解
目录 0.前言1.配置1.建立复制2.断开复制3.安全性4.只读5.传输延迟 2.拓扑1.一主一从结构2.一主多从结构2.树形主从结构 0.前言 说明:该章节相关操作不需要记忆,理解流程和原理即可,用的时候能自主查到即可主从复制? 分布式系统中…...

【算法】leetcode热题100 146.LRU缓存. container/list用法
https://leetcode.cn/problems/lru-cache/description/?envTypestudy-plan-v2&envIdtop-100-liked 实现语言:go lang LRU 最近最少未使用,是一种淘汰策略,当缓存空间不够使用的时候,淘汰一个最久没有访问的存储单元。目前…...

[论文总结] 深度学习在农业领域应用论文笔记13
文章目录 1. Downscaling crop production data to fine scale estimates with geostatistics and remote sensing: a case study in mapping cotton fibre quality (Precision Agriculture ,2024, IF5.585)背景方法结果结论个人总…...
《Detection of Tea Leaf Blight in Low-Resolution UAV Remote Sensing Images》论文阅读
学习资料 论文题目:Detection of Tea Leaf Blight in Low-Resolution UAV Remote Sensing Images(低分辨率UAV遥感图像中茶叶枯萎病的检测)论文地址:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber10345618 Abstr…...
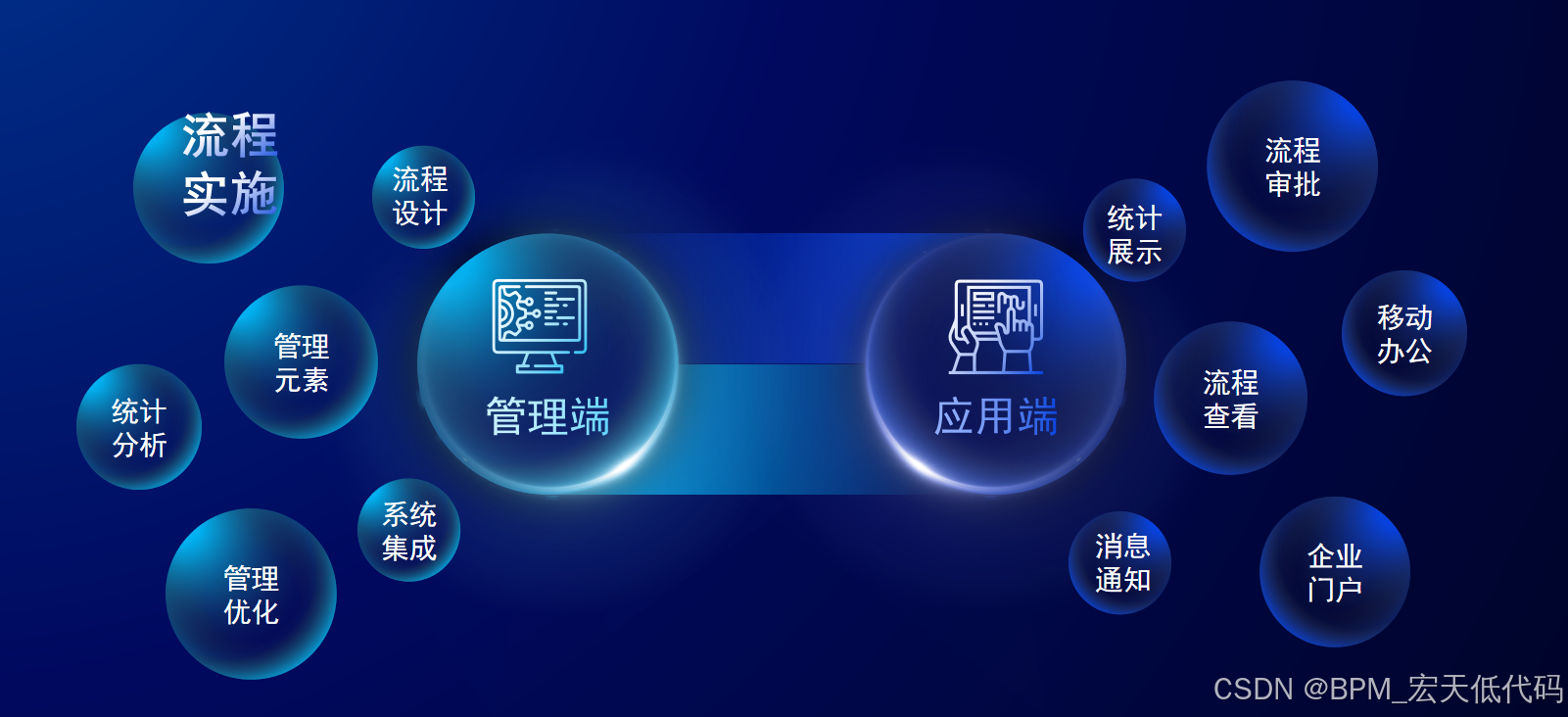
低代码BPA(业务流程自动化)技术探讨
一、BPA流程设计平台的特点 可视化设计工具 大多数BPA流程设计平台提供直观的拖拽式界面,用户可以通过图形化方式设计、修改及优化业务流程。这种可视化的方式不仅降低了门槛,还便于非技术人员理解和参与流程设计。集成能力 现代BPA平台通常具备与其他系…...
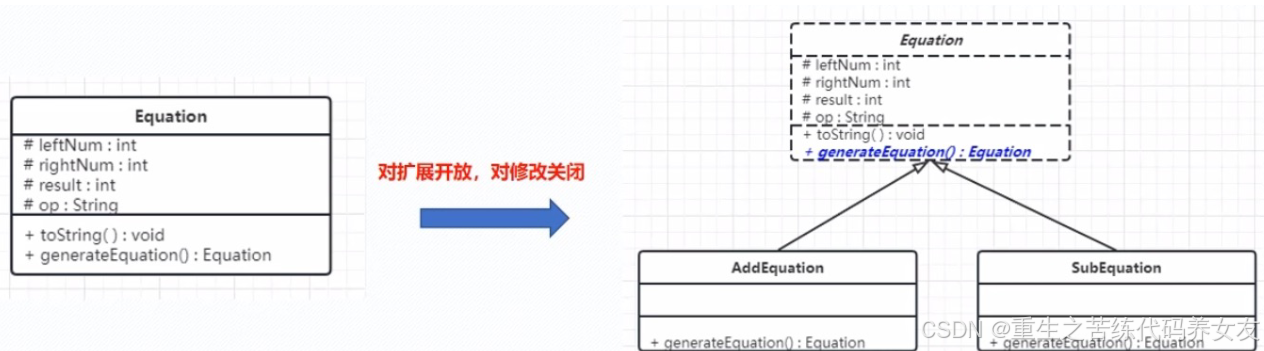
开闭原则(OCP)
开闭原则(OCP):Open Closed Princide:对扩展开放,对修改关闭。在程序需要进行拓展的时候,不能去修改原有代码,实现一个热插拔的效果。 简言之,是为了使程序的扩展性更好,…...

Unity之 TextMeshPro 介绍
TextMeshPro 是 Unity 中用于处理文本显示的高级插件,旨在替代 Unity 内置的 UI.Text 和 TextMesh 组件。与默认的文本组件相比,TextMeshPro 提供了更高的文本渲染质量和更多的文本样式选项,同时具备强大的优化能力。 TextMeshPro 的主要特点…...
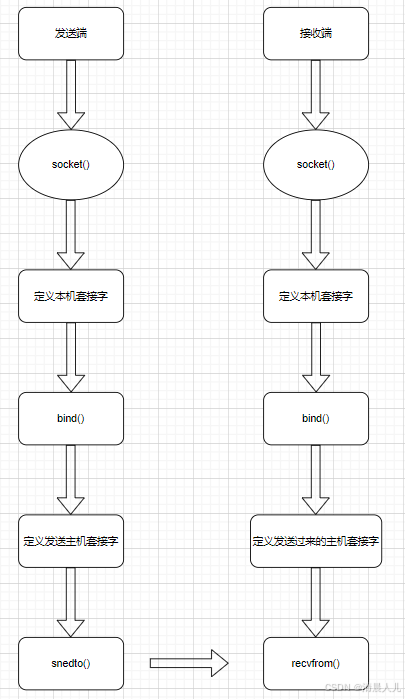
Linux套接字Socket
Linux套接字Socket 前提知识补充 为不同机器上的两个进程之间提供通信机制 主机字节序小端存储,网络字节序大端存储 特点TCPUDP连接类型面向连接无连接可靠性高低有序性保证数据包按顺序到达不保证数据包顺序流量控制有滑动窗口机制无拥塞控制有拥塞控制机制无复杂性较高较低…...
基于 Web 的工业设备监测系统:非功能性需求与标准化数据访问机制的架构设计
目录 案例 【说明】 【问题 1】(6 分) 【问题 2】(14 分) 【问题 3】(5 分) 【答案】 【问题 1】解析 【问题 2】解析 【问题 3】解析 相关推荐 案例 阅读以下关于 Web 系统架构设计的叙述,回答问题 1 至问题 3 。 【说明】 某公司拟开发一款基于 Web 的…...

【MySQL】基础入门篇
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:理解什么是MySQL,如何安装MySQL,简单使用MySQL。 > 毒鸡汤:有些事情,总是不明白,所以我不…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
