当前位置： 首页 > news >正文

3d gaussian splatting公式推导

news 2025/7/8 3:56:43

1. 离散公式推导

nerf中连续的积分渲染公式是：

C(r)=\int_{0}^{t_i}T(t)\sigma(r(t))c(r(t), d)dt

其中被遮挡率：

T(t)=exp(-\int_{0}^{t_i}\sigma(r(s))ds)

那么转换为离散公式后有：

T_i=T(t_i) =exp(-\sum_{j=0}^{j=i-1}\int_{t_j}^{t_{j+1}}\sigma(t)dt) =exp(-\sum_{j=0}^{j=i-1}\sigma_j\delta_j)

其中，\delta_j代表j时刻的时间差，将其带入渲染公式：

C(i)=\sum_{j=0}^{j=i-1}\int_{t_j}^{t_{j+1}}T(t)\sigma(t)c(t)dt \\=\sum_{j=0}^{j=i-1}\int_{t_j}^{t_{j+1}}exp(-\int_{0}^{t}\sigma(s)ds)\sigma_jc_jdt \\=\sum_{j=0}^{j={i-1}}\int_{t_j}^{t_{j+1}}exp(-\int_{0}^{t_j}\sigma(s)ds)exp(-\int_{t_j}^{t}\sigma(s)ds)\sigma_jc_jdt \\=\sum_{j=0}^{j=i-1}\int_{t_j}^{t_{j+1}}T_jexp(-\int_{t_j}^{t}\sigma(s)ds)\sigma_jc_jdt \\=\sum_{j=0}^{j=i-1}T_j\sigma_jc_j\int_{t_j}^{t_{j+1}}exp(-\sigma_j(t-t_j)dt \\=\sum_{j=0}^{j=i-1}T_j\sigma_jc_j(-\frac{1}{\sigma_j})(exp(-\sigma_j\delta_j)-1) \\=\sum_{j=0}^{j=i-1}T_jc_j(1-exp(-\sigma_j\delta_j))

设透明度    \alpha_i=(1-exp(-\sigma_i\delta_i))

则被遮挡率   T_i =\prod_{j=1}^{j=i-1}(1-\alpha_i)

有   C(i)=\sum_{j=0}^{j=i-1}c_j\alpha_j\prod_{j=1}^{j=i-1}(1-\alpha_j)

而gaussian-splating的公式与nerf不一样的点在于，透明度\alpha_i的计算是根据像素点处于2D高斯球的概率求得的：

\alpha_i=\frac{1}{2\pi\sqrt{\left | \Omega \right |}}exp(-0.5(x-\mu)\Omega ^{-1}(x-\mu))

其中\mu是3D高斯球溅射到屏幕上形成的2D高斯球的均值，\Omega是2D高斯球的协方差

2. 正向渲染公式推导

正向渲染是指从3D高斯球渲染到2D屏幕中某个像素值的颜色的过程。

2.1 3D高斯到2D高斯

首先，3D高斯参数有高斯球的中心即均值\omega，协方差\Sigma，透明度\sigma，颜色c，2D高斯参数有高斯球的中心即均值\mu，协方差\Omega。

对于均值\mu来说，其值就是将\omega转换到屏幕坐标系上就可以了

p_{c}=T_{w2c}\omega，p_c将\omega从世界坐标系转换到相机坐标系下，

\mu=\left\{\begin{matrix}p_c[0]/p_c[2] \\ p_c[1]/p_c[2] \\ \left \| p_c \right \| \end{matrix}\right.

这里3D高斯球的表示是通过一个旋转R和一个缩放矩阵S的乘积表示的，即\Sigma=RS\Lambda S^TR^T=RSS^TR^T,这么表示的原理是协方差是一个椭球，标准正态分布是一个圆，椭球就是将这个圆进行旋转缩放变成的。\Lambda是标准正态分布的协方差，它是一个单位矩阵，所以可以省略。

3. 反向传播公式推导

参考：

【CV】Nerf中体素渲染的离散公式推导 - Edlinf - 博客园

https://zhuanlan.zhihu.com/p/633106694

相关文章：

3d gaussian splatting公式推导

1. 离散公式推导 nerf中连续的积分渲染公式是： 其中被遮挡率： 那么转换为离散公式后有： 其中，代表j时刻的时间差，将其带入渲染公式： 设透明度 则被遮挡率 有 而gaussian-splating的公式与ner…...

编程日记 2024/9/26 10:52:44

金属增材制造咋突破？纳米纹理粉末如何助力金属增材制造？

大家好，今天我们来了解一篇金属增材制造文章——《High absorptivity nanotextured powders for additive manufacturing》发表于《Science Advances》。金属增材制造在医疗、航空航天等领域，它潜力巨大，但目前可打印的金属材料有限&#xff…...

编程日记 2024/9/26 10:50:41

openpnp - 为了防止物料操作混乱，做一张物料分布位置图清晰一些

文章目录 openpnp - 为了防止物料操作混乱，做一张物料分布位置图清晰一些概述笔记做子装配图做总装配图备注END openpnp - 为了防止物料操作混乱，做一张物料分布位置图清晰一些 概述 看网上资料，当openpnp贴片机上料后，为了防止…...

编程日记 2024/9/26 10:48:38

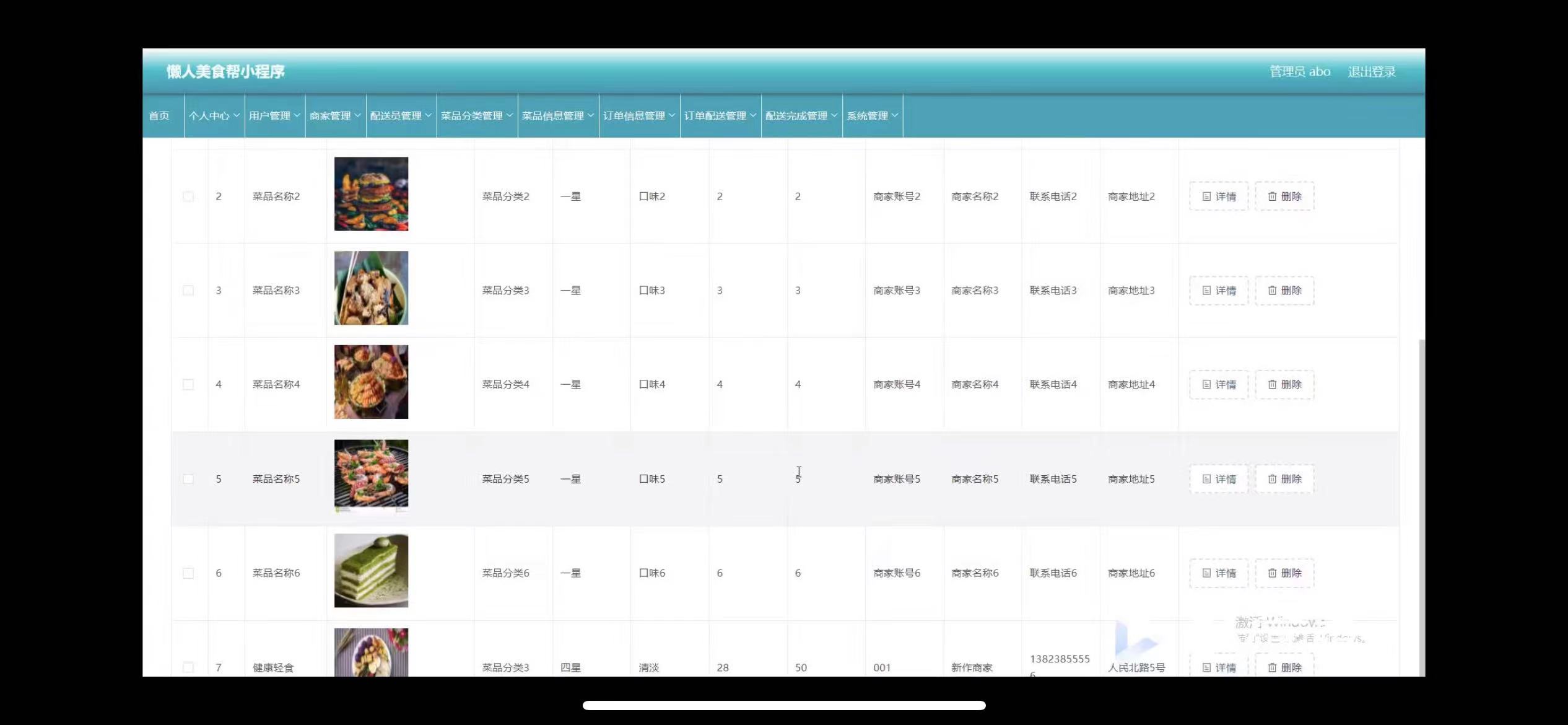
懒人帮美食系统小程序的设计

管理员账户功能包括：系统首页，个人中心，用户管理，商家管理，配送员管理，菜品分类管理，菜品信息管理，订单信息管理，订单配送管理 微信端账号功能包括：系统首页…...

编程日记 2024/9/26 10:47:37

David律所代理Jose Martin幽默水果版权首发维权，尚未TRO

案件基本情况：起诉时间：2024/9/18案件号：2024-cv-08484原告：Jose Martin原告律所：David起诉地：伊利诺伊州北部法院涉案商标/版权：原告品牌简介：西班牙的卓越艺术家Jose Martin以他非…...

编程日记 2024/9/26 10:46:35

读构建可扩展分布式系统：方法与实践15可扩展系统的基本要素

1. 可扩展系统的基本要素 1.1. 分布式系统在本质上就是复杂的，你必须考虑多种故障模式，并设计应对所有可能发生的情况的处理方式 1.2. 大规模应用程序需要协调大量的硬件和软件组件，共同实现低延迟和高吞吐量的能力 1.3. 面临的挑战是将所…...

编程日记 2024/9/26 10:45:34

解决VisualStudio msvsmon.exe远程调试器未启动问题

原本好好的用本地调试器编译运行程序，结果VisualStudio不知道哪根筋抽风了，死活就是无法运行程序。 心想是不是程序问题，结果直接运行程序没问题。 心想是不是msvsmon.exe是个后台服务，结果死活找不到这个服务，然后再…...

编程日记 2024/9/26 10:44:33

如果淘汰是注定的，那么读书还有意义吗？

哪吒说：“我命由我不由天，是魔是仙我自己说了算。”； 而且书中自有颜如玉，书中自有黄金屋； 抛开以上说法，有一句话说的也特别好：“人这一辈子，赚不到自己认知以外的钱，没…...

编程日记 2024/9/26 10:41:30

Python 中 三种常用的绘图方式 ! ! !

一 Matplotlib可视化 在Python中，Matplotlib是一个功能强大的绘图库，特别是其Pyplot模块，提供了类似于MATLAB的绘图接口，使得用户可以轻松绘制各种2D图表。下面我们将详细介绍使用Matplotlib进行可视化的基本步骤以及常用图形的…...

编程日记 2024/9/26 10:40:28

统一回复OneAPI:failed to get gpt-3.5-turbo token encoder的解决办法

源码方式安装后启动OneAPI时提示failed to get gpt-3.5-turbo token encode，缺少编码文件的解决办法。 1、编辑encoding.go文件 vim /root/go/pkg/mod/github.com/pkoukk/tiktoken-gov0.1.7/encoding.go 注意：tiktoken-gov0.1.7要根据实际情况&#x…...

编程日记 2024/9/26 10:39:27

Flash Attention是怎么做到又快又省显存的？

Flash Attention 并没有减少 Attention 的计算量，也不影响精度，但是却比标准的Attention运算快 2~4 倍的运行速度，减少了 5~20 倍的内存使用量。究竟是怎么实现的呢？ Attention 为什么慢？ 此处的“快慢”是相对而言的…...

编程日记 2024/9/26 10:38:26

CAN报文ID过滤

在CAN通信中，CAN_FILTERMODE_LIST和CAN_FILTERMODE_MASK是用于CAN过滤器配置的两种不同过滤模式。 1. CAN_FILTERMODE_LIST： - 当CAN过滤器使用CAN_FILTERMODE_LIST模式时，过滤器将匹配通过滤器的标识符列表中的任何一个标识符。换句话说…...

编程日记 2024/9/26 10:36:23

ELK-05-skywalking监控SpringCloud服务日志

文章目录 前言一、引入依赖二、增加日志配置文件三、打印日志四、skywalking网页查询链路五、日志收集5.1 修改logback-spring.xml5.2 重启SpringCloud服务并请求test接口5.3 查看skywalking网页的Log 总结 前言 基于上一章节，现在使用skywalkin监控SpringCloud服务…...

编程日记 2024/9/26 10:30:14

17年数据结构考研真题解析

第一题&#xff1a; 解析&#xff1a; 我们说递归要找出口&#xff0c;这道题的出口是sum<n&#xff0c;经过观察可以得知&#xff1a;sum123。。。k 设第k次循环跳出&#xff0c;则有sum123。。。k<n k<,很显然答案选B 第二题&#xff1a; 解析&#xff1a; 第一句&a…...

编程日记 2024/9/26 10:28:11

nginx 安装（Centos）

nginx 安装-适用于 Centos 7.x [rootiZhp35weqb4z7gvuh357fbZ ~]# lsb_release -a LSB Version: :core-4.1-amd64:core-4.1-noarch Distributor ID: CentOS Description: CentOS Linux release 7.9.2009 (Core) Release: 7.9.2009 Codename: Core# 创建文件…...

编程日记 2024/9/26 10:27:10

异步编程利器：深入解析 Python 异步并发库 Gevent

在现代 Python 应用开发中&#xff0c;并发编程 是提高程序性能、处理多个任务的关键手段之一。虽然 Python 有原生的多线程、多进程模块&#xff0c;但这些模块存在一些限制&#xff0c;比如全局解释器锁&#xff08;GIL&#xff09;会影响多线程程序的执行效率。此外&#xf…...

编程日记 2024/9/26 10:26:09

Python pyusb 使用指南【windows+linux】

前言&#xff1a;USB(通用串行总线)作为一种高度通用性的硬件接口&#xff0c;在诸多领域均有应用。在C中可以直接使用libusb库即可完成USB设备信息查询、USB设备监听、与USB设备控制端点、数据&#xff08;同步、批量、中断&#xff09;端点进行指令、数据交互等功能。python中…...

编程日记 2024/9/26 10:25:07

Xcode报错：The request was denied by service delegate (SBMainWorkspace)

Xcode报错&#xff1a;The request was denied by service delegate (SBMainWorkspace) 造成的原因: &#xff08;1&#xff09;新的M2芯片的Mac电脑 (2) 此电脑首次安装启动Xcode的应用程序 (3&#xff09;此电脑未安装Rosetta 解决方法: &#xff08;1&#xff09;打开终端…...

编程日记 2024/9/26 10:24:06

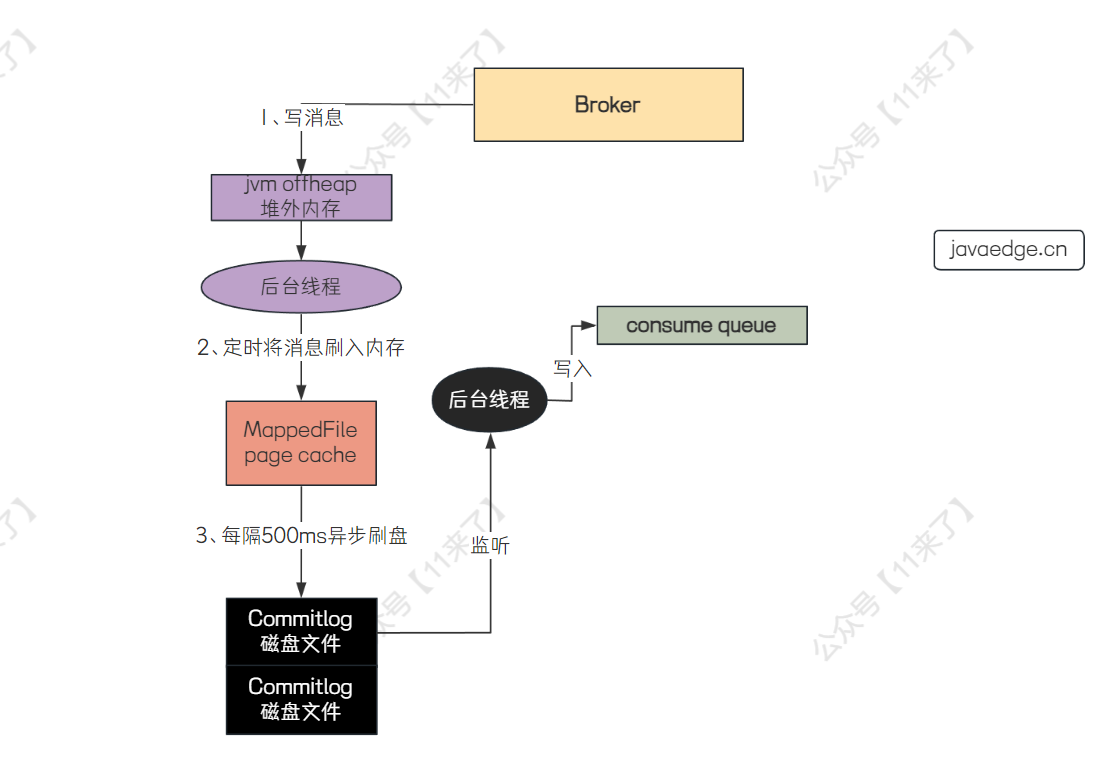
面试系列-携程暑期实习一面

Java 基础 1、Java 中有哪些常见的数据结构&#xff1f; 图片来源于&#xff1a;JavaGuide Java集合框架图 Java 中常见的数据结构包含了 List、Set、Map、Queue&#xff0c;在回答的时候&#xff0c;只要把经常使用的数据结构给说出来即可&#xff0c;不需要全部记住 如下&…...

编程日记 2024/9/26 10:23:05

你以为建站很复杂？Baklib 5分钟解决你的痛点

你以为建站很复杂&#xff1f;Baklib 5分钟解决你的痛点&#xff01; 在这个“快节奏”的互联网时代&#xff0c;想要快速搭建一个网站是很多人的刚需。今天我要介绍的&#xff0c;就是如何利用Baklib的CMS/Wiki模板&#xff0c;五分钟内让你的网站“横空出世”。废话不多说&am…...

编程日记 2024/9/26 10:22:03

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/6/20 13:53:42

Qt Widget类解析与代码注释

#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码&#xff0c;写上注释 当然可以&#xff01;这段代码是 Qt …...

编程新知 2025/6/15 21:47:30

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2025/7/7 20:14:35

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库&#xff0c;例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体&#xff0c;比如 SnowballFight、Huggy the Do…...

编程新知 2025/6/26 3:44:44

爬虫基础学习day2

# 爬虫设计领域 工商&#xff1a;企查查、天眼查短视频&#xff1a;抖音、快手、西瓜 ---> 飞瓜电商&#xff1a;京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空&#xff1a;抓取所有航空公司价格 ---> 去哪儿自媒体&#xff1a;采集自媒体数据进…...

编程新知 2025/7/6 13:55:34

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2025/7/7 0:36:08

NPOI Excel用OLE对象的形式插入文件附件以及插入图片

static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

编程新知 2025/6/21 14:09:32

基于单片机的宠物屋智能系统设计与实现（论文+源码）

本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢&#xff0c;连接红外测温传感器&#xff0c;可实时精准捕捉宠物体温变化&#xff0c;以便及时发现健康异常&#xff1b;水位检测传感器时刻监测饮用水余量&#xff0c;防止宠物…...

编程新知 2025/7/5 13:39:22

Python学习(8) ----- Python的类与对象

Python 中的类&#xff08;Class&#xff09;与对象&#xff08;Object&#xff09;是面向对象编程&#xff08;OOP&#xff09;的核心。我们可以通过“类是模板&#xff0c;对象是实例”来理解它们的关系。 &#x1f9f1; 一句话理解&#xff1a; 类就像“图纸”&#xff0c;对…...

编程新知 2025/6/19 6:06:53

起重机起升机构的安全装置有哪些？

起重机起升机构的安全装置是保障吊装作业安全的关键部件&#xff0c;主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理&#xff1a; 一、超载保护装置&#xff08;核心安全装置&#xff09; 1. 起重量限制器 功能&#xff1a;实时监测起升载荷&a…...

编程新知 2025/6/21 17:50:22