Flash Attention是怎么做到又快又省显存的？

Flash Attention 并没有减少 Attention 的计算量，也不影响精度，但是却比标准的Attention运算快 2~4 倍的运行速度，减少了 5~20 倍的内存使用量。究竟是怎么实现的呢？

Attention 为什么慢？

此处的“快慢”是相对而言的。严格意义上来说，相比于传统的 RNN，Transformer中的Attention可以并行地处理序列所有位置的信息（RNN 只能串行处理），因此计算效率并不低，但是仍然有可以进一步改进的空间。

众所周知，科学计算通常分为计算密集型 (compute-bound) 和内存密集型 (memory-bound) 两类。其中，计算密集型运算的时间瓶颈主要在于算数计算，比如大型矩阵的相乘等，而内存密集型运算的时间瓶颈主要在于内存的读写时间，比如批归一化、层归一化等等。

• 时间复杂度：Attention 需要对矩阵 Q 和矩阵 K 的转置做乘法来得到注意力权重矩阵。不考虑 batch 维度，假设矩阵QK 的尺寸都为$(n,dim)$，那么两个维度为$(n,dim)$的矩阵相乘的时间复杂度是序列长度n的平方级$O(n^2)$；在计算完注意力权重矩阵后，还需要对其进行softmax操作，这个算法需要分成三次迭代来执行$O(n^3)$
• 空间复杂度：Attention的计算过程需要存储$S=Q{K}^T$和$P=softmax(S)$这两个尺寸均为$(n,n)$的矩阵

为了对 Attention 的内存读取时间有更清晰的感知，这里简单介绍 GPU 的内存层级。

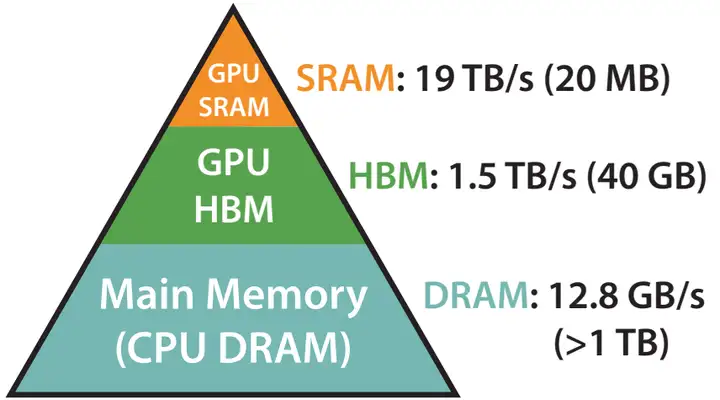
GPU 的内存可以分为 HBM 和 SRAM 两部分。例如，A100 GPU具有40-80 GB的高带宽内存（上图中的 HBM，即我们平时说的“显存”），带宽为 1.5TB/s，并且108个流式多核处理器都有 192 KB 的片上 SRAM，带宽约为 19 TB/s。片上 SRAM 比 HBM 快一个数量级，但容量要小很多个数量级。

在 GPU 运算之前，数据和模型先从 CPU 的内存（上图中的DRAM）移动到 GPU 的 HBM，然后再从 HBM 移动到 GPU 的 SRAM，CUDA kernel 在 SRAM 中对这些数据进行运算，运算完毕后将运算结果再从 SRAM 移动到 HBM。

所以提高Attention运算效率，需要从降低attention的时间和空间复杂度入手。

时间复杂度

在$S=Q{K}^T$的计算过程中，理论上尝试的方法主要可以分为稀疏 (sparse) 估计和低秩 (low-rank) 估计。但是在实际应用中仍然存在一些缺陷：

• 性能比不上原始 attention。不论是稀疏估计、低秩估计还是其他，这些方法都采用了某种近似算法来估算注意力权重矩阵，难免会丢失信息。目前主流的还是原始的attention
• 无法减少内存读取的时间消耗。这些方法只能降低 attention 的计算复杂度，但是无法对 attention 运算过程中的空间复杂度等进行控制，无法减少内存读写带来的时间损耗

所以在时间复杂度方向的优化主要在softmax的计算过程中：

$$\mathrm{softmax}\left(x_i\right)=\frac{e^{x_i}}{{\sum }_{k=1}^N{e}^{x_k}}$$

softmax 有个问题，那就是很容易溢出。比如float16的最大值为65504，所以只要$x\ge 11$ 的话softmax就溢出了。好在 exp 有这么一个性质，那就是$e^{x-y}=\frac{e^x}{e^y}$，根据这个性质，可以在分子分母上同时除以一个数，这样可以将$x$的范围都缩放到范围内，保证计算 softmax 时的数值稳定性。这个算法可以分成三次迭代来执行：

1. 遍历所有数，求 x 中的最大值m

$$\begin{array}{l}\text{ for }i\leftarrow 1,N\text{ do }\\ m_i=\max \left(m_i,x_i\right)\end{array}$$
2. 计算 softmax 分母，并根据m对其进行缩放

$$\begin{array}{rl}\text{ for }i& \leftarrow 1,N\text{ do }\\ d_i& =d_{i-1}+e^{x_i-m_N}\end{array}$$
3. 求对应位置的 softmax

$$\begin{array}{rl}\text{ for }i& \leftarrow 1,Ndo\\ a_i& =\frac{e^{x_i-m_N}}{d_N}\end{array}$$

分析以上步骤可以发现，如果是不做任何优化的话，至少要进行和 GPU 进行6次通信（3次写入，3次写出），如果对每一步的for循环进行一些并行切分的的话，还要加上 reduce_sum 和 reduce_max 之类的通信成本。所以2018年 Nvidia 提出了《Online normalizer calculation for softmax》，核心改进是去掉第二步$d_i=d_{i-1}+e^{x_i-m_N}$中对$m_N $的依赖，设$d_{i}^{{\prime}=\sum_{j}}{i} e^{x_{j}-m_{i}}$（这里的全局最大值变成了当前最大值），这个式子有如下的性质：

$$\begin{array}{rl}{d}_i^{\prime }& =\sum _j^i{e}^{x_j-m_i}\\ & =\sum _j^{i-1}{e}^{x_j-m_i}+e^{x_i-m_i}\\ & =\sum _j^{i-1}{e}^{x_j-m_{i-1}+m_{i-1}-m_i}+e^{x_i-m_i}\\ & =\left(\sum _j^{i-1}{e}^{x_j-m_{i-1}}\right)e^{m_{i-1}-m_i}+e^{x_i-m_i}\\ & =d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}+e^{x_i-m_i}\end{array}$$

这个式子依赖于$d_{i-1}^{\prime }，m_i，m_{i-1}$。那么就可以将softmax前两步合并到一起：

1. 求 x 的最大值 m, 计算 softmax 的分母

$$\begin{array}{l}\text{ for }i\leftarrow 1,N\text{ do }\\ m_i=\max \left(m_i,x_i\right)\\ d_i^{\prime }=d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}+e^{x_i-m_i}\end{array}$$
2. 求对应位置的 softmax

$$\begin{array}{rl}\text{ for }i& \leftarrow 1,Ndo\\ a_i& =\frac{e^{x_i-m_N}}{d_N}\end{array}$$

以上的算法优化可以将3步合并变成2步，将softmax的时间复杂度降为$O(n^2)$。

空间复杂度

在将3步合成2步的同时：

• 借助GPU的share memory来存储中间结果，将上面的两步只用一个 kernel 实现，这样就只需要与 global memory 通信两次（一次写入数据，一次读取结果）
• 还可以减少 Reduce_max 和 Reduce_sum 之类的通信成本

空间复杂度方面优化的基本思路是降低Attention对于显存的需求，减少HBM和SRAM之间的换入换出，充分利用 GPU 的并行优势，进而减少Attention运算的时间消耗。

总结

Flash Attention的动机是尽可能避免大尺寸的注意力权重矩阵在 HBM 和 SRAM 之间的换入换出。论文中具体方法包含两个部分：tiling 和 recomputation。

tiling 的基本思路：不直接对整个输入序列计算注意力，而是将其分为多个较小的块，逐个对这些块进行计算，增量式地进行 softmax 的规约。规约过程中只需要更新某些中间变量，不需要计算整个注意力权重矩阵，就是以上介绍的将三部合并成两步的过程。

recomputation 的基本思路：基于 tiling 技巧，在反向传播过程中不保留整个注意力权重矩阵，而是只保留前向过程中 tiling 的某些中间变量，然后在反向传播过程中重新计算注意力权重矩阵。recomputation 可以看作是一种基于 tiling 的特殊的 gradient checkpointing，想进一步了解 recomputation 的读者可以翻阅Flash Attention原文。

得益于上述技巧，Flash Attention 可以同时做到又快（运算速度快）又省（节省显存）。