【蓝桥杯-筑基篇】动态规划
🍓系列专栏:蓝桥杯
🍉个人主页:个人主页
目录
1.最大连续子段和
2.LCS 最大公共子序列
3.LIS 最长上升子序列
4.数塔
5.最大子矩阵和
6.背包问题
①01背包问题
②完全背包
1.最大连续子段和
这段代码是一个求最大子数组和的算法,使用的是动态规划的思想。下面是代码的解释:
首先定义了一个整数数组arr,用于存储给定的一组数。然后定义了一个整数数组dp,用于存储以arr中每个元素为结尾的最大子数组和。接着将dp的第一个元素设置为0和arr的第一个元素的最大值。然后从第二个元素开始循环遍历数组dp,将当前元素的dp设置为 :前一个元素的dp 和 当前元素的arr之和 与 当前元素的arr 比较最大值。最后按升序对数组dp进行排序,最大子数组和即为dp的最后一个元素。
public class A {
public static void main(String[] args) {int arr[]= {-2,11,-4,13,-5,-2}; //定义一个数组arrint dp[]=new int[arr.length]; //定义一个数组dp,长度与arr相同System.out.println("arr:"+Arrays.toString(arr)); //输出arr数组System.out.println("-----------流程-----------"); //输出分割线dp[0]=Math.max(0, arr[0]); //dp[0]为arr[0]和0的最大值System.out.println("dp:"+Arrays.toString(dp)); //输出dp数组for (int i = 1; i < dp.length; i++) { //循环dp数组dp[i]=Math.max(dp[i-1]+arr[i], arr[i]); //dp[i]为dp[i-1]+arr[i]和arr[i]的最大值System.out.println("dp[i-1]+arr[i]:"+(dp[i-1]+arr[i])+"\narr[i]:"+arr[i]); //输出dp[i-1]+arr[i]和arr[i]System.out.println("dp:"+Arrays.toString(dp)); //输出dp数组}Arrays.sort(dp); //对dp数组进行排序System.out.println("-----------流程-----------"); //输出分割线System.out.println("最大字段和:"+dp[dp.length-1]); //输出dp数组中的最大值
}arr:[-2, 11, -4, 13, -5, -2]
-----------流程-----------
dp:[0, 0, 0, 0, 0, 0]
dp[i-1]+arr[i]:11
arr[i]:11
dp:[0, 11, 0, 0, 0, 0]
dp[i-1]+arr[i]:7
arr[i]:-4
dp:[0, 11, 7, 0, 0, 0]
dp[i-1]+arr[i]:20
arr[i]:13
dp:[0, 11, 7, 20, 0, 0]
dp[i-1]+arr[i]:15
arr[i]:-5
dp:[0, 11, 7, 20, 15, 0]
dp[i-1]+arr[i]:13
arr[i]:-2
dp:[0, 11, 7, 20, 15, 13]
-----------流程-----------
最大字段和:20分治法:
最大字段和(分治法,递归,Java)
2.LCS 最大公共子序列
例如:
S1={1,5,2,8,9,3,6},S2={5,6,8,9,3,7},其最大公共子序列为{5,8,9,3}。
为了找到两个字符串之间的最大公共子序列,我们可以使用动态规划。基本思想是创建一个矩阵,其中每个单元格表示到该点的最大公共子序列的长度。
我们从将矩阵的第一行和第一列初始化为0开始。然后,对于每个后续单元格,我们检查两个字符串中相应位置的字符是否匹配。如果匹配,则将当前单元格的左上角对角线上的值加1。如果不匹配,则取当前单元格上方和左侧单元格之间的最大值。
填充整个矩阵后,最长公共子序列的长度可以在右下角单元格中找到。

public class A {
public static void main(String[] args) {String s1="BDCABA";String s2="ABCBDAB";int dp[][]=new int[s1.length()+1][s2.length()+1];for (int i = 0; i < s1.length(); i++) {for (int j = 0; j < s2.length(); j++) {if(s1.charAt(i)==s2.charAt(j)) dp[i+1][j+1]=dp[i][j]+1;else dp[i+1][j+1]=Math.max(dp[i+1][j], dp[i][j+1]);}}for (int[] is : dp) {for (int i : is) {System.out.print(i+" ");}System.out.println();}System.out.println("最大公共子序列:"+dp[s1.length()][s2.length()]);}
}
0 0 0 0 0 0 0 0
0 0 1 1 1 1 1 1
0 0 1 1 1 2 2 2
0 0 1 2 2 2 2 2
0 1 1 2 2 2 3 3
0 1 2 2 3 3 3 4
0 1 2 2 3 3 4 4
最大公共子序列:4
3.LIS 最长上升子序列

动态规划解决方案的基本思想是使用一个数组 dp 来跟踪输入数组中每个索引处的最长上升子序列的长度。我们将dp初始化为所有 1,因为任何索引处的最长上升子序列长度至少为 1(元素本身)。然后,我们遍历输入数组,并对于每个元素,我们遍历所有先前的元素并检查它们是否小于当前元素。如果是,我们将当前索引处的 dp更新为其当前值和前一个索引处的值加 1 的最大值。这意味着我们已经找到了以当前索引结尾的更长的上升子序列。最后,我们输出 dp 中的最大值,它表示输入数组中最长上升子序列的长度。
public class A {
public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt(); //输入数组长度int arr[]=new int[n]; //定义数组for (int i = 0; i < arr.length; i++) {arr[i]=scanner.nextInt(); //输入数组元素}int dp[]=new int[arr.length]; //定义dp数组Arrays.fill(dp, 1); //初始化dp数组int j=0;for (int i = 1; i < arr.length; i++) {j=i-1;while (j>=0) { if(arr[i]>arr[j]) { //如果当前元素大于前面的元素dp[i]=Math.max(dp[i], dp[j]+1); //更新dp数组}j--;}}System.out.println(Arrays.toString(dp)); //输出dp数组Arrays.sort(dp); //对dp数组进行排序System.out.println(dp[dp.length-1]); //输出dp数组中的最大值
}
}输入:
7
1 5 2 3 11 7 9输出:
[1, 2, 2, 3, 4, 4, 5]
54.数塔
【动态规划】——数塔(java版,超详图解)
5.最大子矩阵和
知识点:前缀和+动态规划【最大字段和】
【蓝桥杯-筑基篇】前缀和
了解决这个问题,我们首先读入一个n x n的矩阵,并计算每列的前缀和。然后,对于每对起始和结束列,我们计算它们之间的子矩阵和。
接下来,我们使用动态规划来找到每列的最大子段和,并相应地更新最大子矩阵和。最后,我们输出最大子矩阵和。
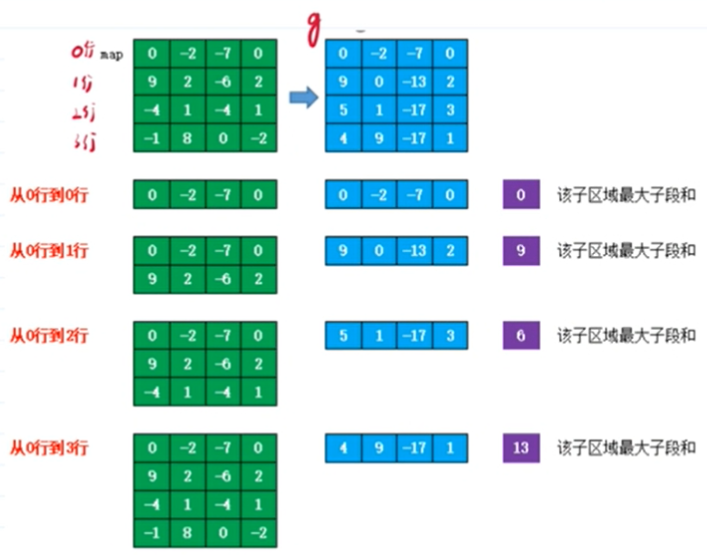

//读入一个n*n的矩阵
//计算每一列的前缀和
//对于每一列的起始和结束位置,计算出这两列之间的子矩阵和
//用dpi表示以第i列为结尾的最大子段和
//对于每一列,计算以该列为结尾的最大子段和,并更新ans
//输出最大子矩阵和public class B {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();int[][] g=new int[n+1][n+1];for (int i = 1; i < g.length; i++) {for (int j = 1; j < g.length; j++) {g[i][j]=scanner.nextInt();g[i][j]=g[i][j]+g[i-1][j]; // 计算每一列的前缀和}}for (int[] is : g) {//输出前缀和数组System.out.println(Arrays.toString(is));}int ans=Integer.MIN_VALUE;for (int start = 1; start < g.length; start++) {for (int end = 1; end < g.length; end++) {int dpi=0;for (int col = 1; col < g.length; col++) {int ai=g[end][col]-g[start-1][col]; // 计算出这两列之间的子矩阵和dpi=Math.max(dpi+ai, ai); // 计算以该列为结尾的最大子段和ans=Math.max(ans, dpi); // 更新ans}}}System.out.println("--最大子矩阵和--:"+ans); // 输出最大子矩阵和}}
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
[0, 0, 0, 0, 0]
[0, 0, -2, -7, 0]
[0, 9, 0, -13, 2]
[0, 5, 1, -17, 3]
[0, 4, 9, -17, 1]
--最大子矩阵和--:15
6.背包问题
①01背包问题
解题思路:使用动态规划算法解决01背包问题,首先输入物品数量和背包容量,然后输入每个物品的重量和价值,接着使用二重循环遍历物品和背包容量,如果当前背包容量大于等于当前物品重量,则可以选择将该物品放入背包,此时背包的价值为dp[i-1][j-wt[i]]+val[i],否则背包的价值为dp[i-1][j],最后输出动态规划数组即可
/*** 01背包问题* wt: 物品重量* val: 物品价值* dp: 动态规划数组*/
public class C {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt(); // 物品数量int m =scanner.nextInt(); // 背包容量int wt[]=new int[n+1]; // 物品重量数组int val[]=new int[n+1]; // 物品价值数组int dp[][]=new int[n+1][m+1]; // 动态规划数组for (int i = 1; i < wt.length; i++) {wt[i]=scanner.nextInt(); // 输入物品重量val[i]=scanner.nextInt(); // 输入物品价值}for (int i = 1; i < wt.length; i++) {for (int j = 1; j <= m; j++) {if(j-wt[i]>=0) {dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-wt[i]]+val[i]); // 动态规划}else dp[i][j]=dp[i-1][j]; // 动态规划}}for (int[] is : dp) {System.out.println(Arrays.toString(is)); // 输出动态规划数组}}}
②完全背包
// 本题为完全背包问题,采用动态规划求解。时间复杂度为O(nW),空间复杂度为O(nW)。
public class C {public static void main(String[] args) {int[] weights = {2, 3, 4, 5}; // 物品重量int[] values = {3, 4, 5, 6}; // 物品价值int capacity = 8; // 背包容量int result = completeKnapsack(capacity,weights, values); // 调用函数System.out.println("Maximum value: " + result); // 输出结果}public static int completeKnapsack(int W, int[] w, int[] v) {int n = w.length; // 物品数量int[][] dp = new int[n+1][W+1]; // 初始化动态规划数组for (int i = 0; i <= n; i++) {dp[i][0] = 0; // 初始化}for (int j = 0; j <= W; j++) {dp[0][j] = 0; // 初始化}for (int i = 1; i <= n; i++) {for (int j = 1; j <= W; j++) {for(int k=0;k<=(j/w[i-1]);k++) {dp[i][j] = Math.max(dp[i][j], dp[i-1][j-k*w[i-1]]+k*v[i-1]); // 状态转移方程}}}return dp[n][W]; // 返回最大价值}}相关文章:

【蓝桥杯-筑基篇】动态规划
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 1.最大连续子段和 2.LCS 最大公共子序列 3.LIS 最长上升子序列 4.数塔 5.最大子矩阵和 6.背包问题 ①01背包问题 ②完全背包 1.最大连续子段和 这段代码是一个求最大子数组和的算法,使用…...

Unity利用Photon PUN2框架快速实现多人在线游戏实例分享
简介 Photon 是一个泛用性的 ScoketServer 套装软件,可用于多人在线游戏、聊天室、大厅游戏,并同时支持 Windows、Unity3D、iOS、Android、Flash 等平台。Photon 包含两个部分,一部分是 Socket 服务器,另一部分是其针对各个平台编写的 SDK,Unity3D 平台对应的 SDK 为 Pho…...

ChatGPT直出1.5w字论文查重率才30% - 基于物联网技术的智能家居控制系统设计与实现
文章目录ChatGPT直出1.5w字论文查重率才30% - 基于物联网技术的智能家居控制系统设计与实现一、绪论1.1 研究背景与意义1.2 国内外研究现状分析1.3 研究内容与目标1.4 研究方向和思路二、物联网技术与智能家居概述2.1 物联网技术原理与应用2.2 智能家居的概念与发展历程2.3 智能…...

特斯拉的操作系统是用什么语言编写的?
总目录链接>> AutoSAR入门和实战系列总目录 文章目录特斯拉车辆操作系统特斯拉GitHub中使用的语言Ruby和GoPythonSwift 和 Objective CQt我们知道操作系统至少需要一些非常低级的代码,这些代码在系统首次启动时运行,必须使用接近硬件的语言编写。…...
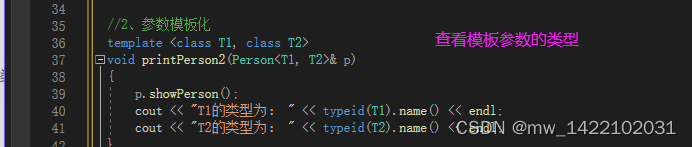
C++学习8-C++提高编程
文章目录前言一、模板1.1 模板的概念1.2 函数模板1.2.1 函数模板语法1.2.2 函数模板注意事项1.2.3 函数模板案例复习:计算数组长度1.2.4 普通函数与函数模板的区别1.2.5 普通函数与函数模板的调用规则1.2.6 模板的局限性1.3 类模板1.3.1 类模板语法1.3.2 类模板与函…...

ubuntu安装git server
一安装 要在Ubuntu上安装Git服务器,需要按照以下步骤进行操作: 安装Git: sudo apt-get update sudo apt-get install git 创建一个Git用户和一个Git仓库目录: sudo adduser git sudo mkdir /home/git/repo.git sudo chown git:git /home/git/repo.git 初始化Git仓库: c…...

物流云数据分析平台
物流云数据分析服务平台 http://project.webcats.cn/bx/36569/2455/index.html 本次系统模拟的是湖南省数据,解释权归杭氏集团所有! 1、系统简介: 物流大数据集成展示系统旨在通过大屏幕全面显示指定地区的物流运营车辆、物流公司和货主的相关信息和…...
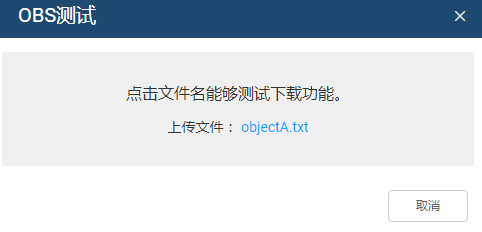
配置OBS存储功能、新搭建obs
通过应用开发环境与OBS(Object-based Storage Service)对接,实现对象或者Widget资产存储功能。 背景信息 对象存储服务(Object-based Storage Service,OBS)是一个基于对象的海量存储服务,为客…...
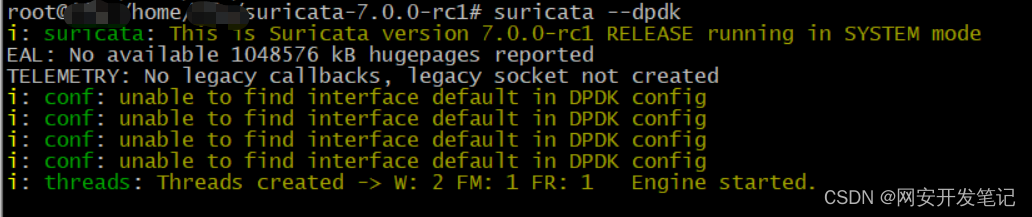
基于DPDK收包的suricata的安装和运行
操作系统版本:Ubuntu 20.04.5 suricata版本: suricata-7.0.0-rc1 suricata是一个基于规则的入侵检测和防御引擎,功能强大,但性能可能 差强人意,不过目前最新的7版本已经支持DPDK收包了,DPDK是Intel提供的高…...
浅谈23种设计模式
创建型模式 有5种设计模式 抽象工厂(Abstract Factory):多套方案 抽象工厂模式是对创建不同的产品类型的抽象。对应到工作中,我们的确应该具备提供多套方案的能力,这也是我们常说的,要提供选择题。当你有这…...
JetBrains Rider 2022.3.3 Crack
具有 ReSharper 强大功能的令人难以置信的 .NET IDE!Rider 在我们使用 Windows 和 macOS 的整个开发团队中使用。 什么是骑士? JetBrains Rider 是一个基于 IntelliJ 平台和 ReSharper 的跨平台 .NET IDE。 支持许多 .NET 项目类型 JetBrains Rider 支持…...

浅理解扁平数据结构转Tree(树形结构)
文章目录📋前言🎯扁平数据结构🎯树形数据结构🎯使用递归将扁平数据转换为树形数据📝最后📋前言 在前端开发中,我们经常需要将扁平数据结构转换为树形结构(Tree)。比如在…...

前端开发——JavaScript的条件语句
世界不仅有黑,又或者白 世界而是一道精致的灰 ——Lungcen 目录 条件判断语句 if 语句 if else 语句 if else if else 语句 switch语句 break 关键字 case 子句 default语句 while循环语句 do while循环语句 for循环语句 for 循环中的三个表达式 for 循环嵌套 for …...

2.11 循环赛日程表
博主简介:一个爱打游戏的计算机专业学生博主主页: 夏驰和徐策所属专栏:算法设计与分析 目录 书本内容: 我的理解: 更优化的算法: 总结 1.注意实现问题 2.当用C语言和C实现循环赛日程表算法时ÿ…...

SpringBoot——SB整合mybatis案例(残缺版本)第三集
了解完使用阿里云存储的操作后,现在需要在案例里面集成阿里云进行开发。云服务——阿里云OSS的入门使用_北岭山脚鼠鼠的博客-CSDN博客 阿里云OSS——集成 对于前端传过来的图片要先上传到OSS,然后获取图片在云端的访问地址,存储到数据库里面…...
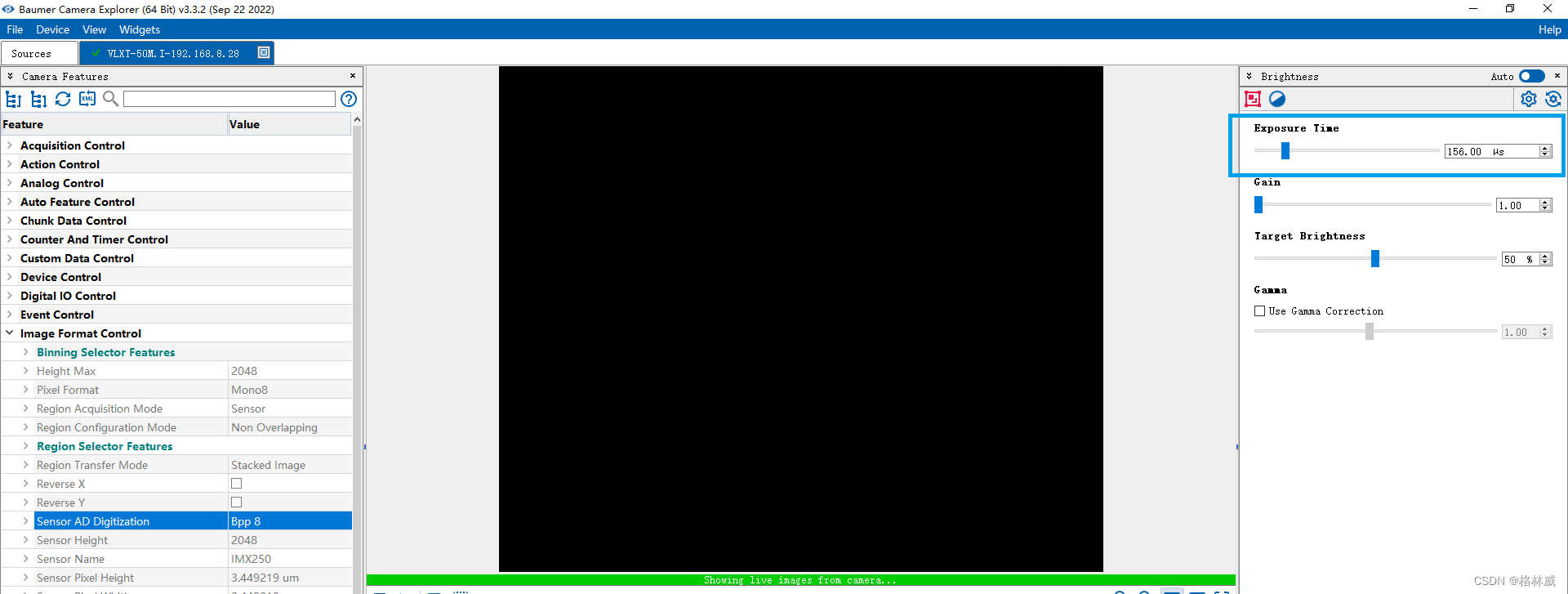
Baumer工业相机堡盟相机不满帧如何使用CameraExplorer设置相机参数让它的帧率达到满帧
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

巴黎爱情回忆 NFT 作品集
由 Metaverse Studio 制作。 欢迎来到浪漫之都巴黎!尽情游览美丽壮观的地标,探索法国文化。在离开之前,别忘了从《巴黎爱情回忆》NFT 作品集中带走一件纪念品。从世界著名的法国人物到标志性资产,这些 NFT肯定会为您的钱包带来巴黎…...
openai开放gpt3.5-turbo模型api,使用python即可写一个基于gpt的智能问答机器人
1安装python库 使用pip安装openai库,注意gpt3.5-turbo模型需要python>3.9的版本支持,本文演示的python版本是python3.10.10 pip install openai2创建api key 需要提前在openai官网上注册好账号,然后打开https://platform.openai.com/ac…...
GUI开发--LCD屏幕的使用(非第三方库)--笔记
导:界面交互需要GUI,GUI需要文字和图片,所有此处总结在M4芯片上实现GUI的基本操作!该芯片具有160K大小的内存,有512K的flash;故而没有使用第三方库! LCD屏幕的使用--笔记 1.汉字显示-两种方式…...

CesiumForUnreal实现地形等高线效果
文章目录 1.实现目标2.实现过程2.1 实现原理2.2 具体过程3.参考资料1.实现目标 在UE5中使用CesiumForUnreal插件添加Cesium World Terrain在线的世界地形,然后以25米为等高距,绘制一定范围内的等高线,如下图所示: 2.实现过程 由于这里直接使用CesiumForUnreal插件加载的在…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
