回溯算法37:解数独
主要是我自己刷题的一些记录过程。如果有错可以指出哦,大家一起进步。
转载代码随想录
原文链接:
代码随想录
leetcode链接:37. 解数独
题目:
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例:
示例 1:

输入:board = [
[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],
[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],
[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],
[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],
[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],
[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],
[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],
[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],
[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:[
[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 '.'
题目数据 保证 输入数独仅有一个解
思路:
棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是二维递归。
怎么做二维递归呢?
N皇后问题是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
因为这个树形结构太大了,我抽取一部分,如图所示:
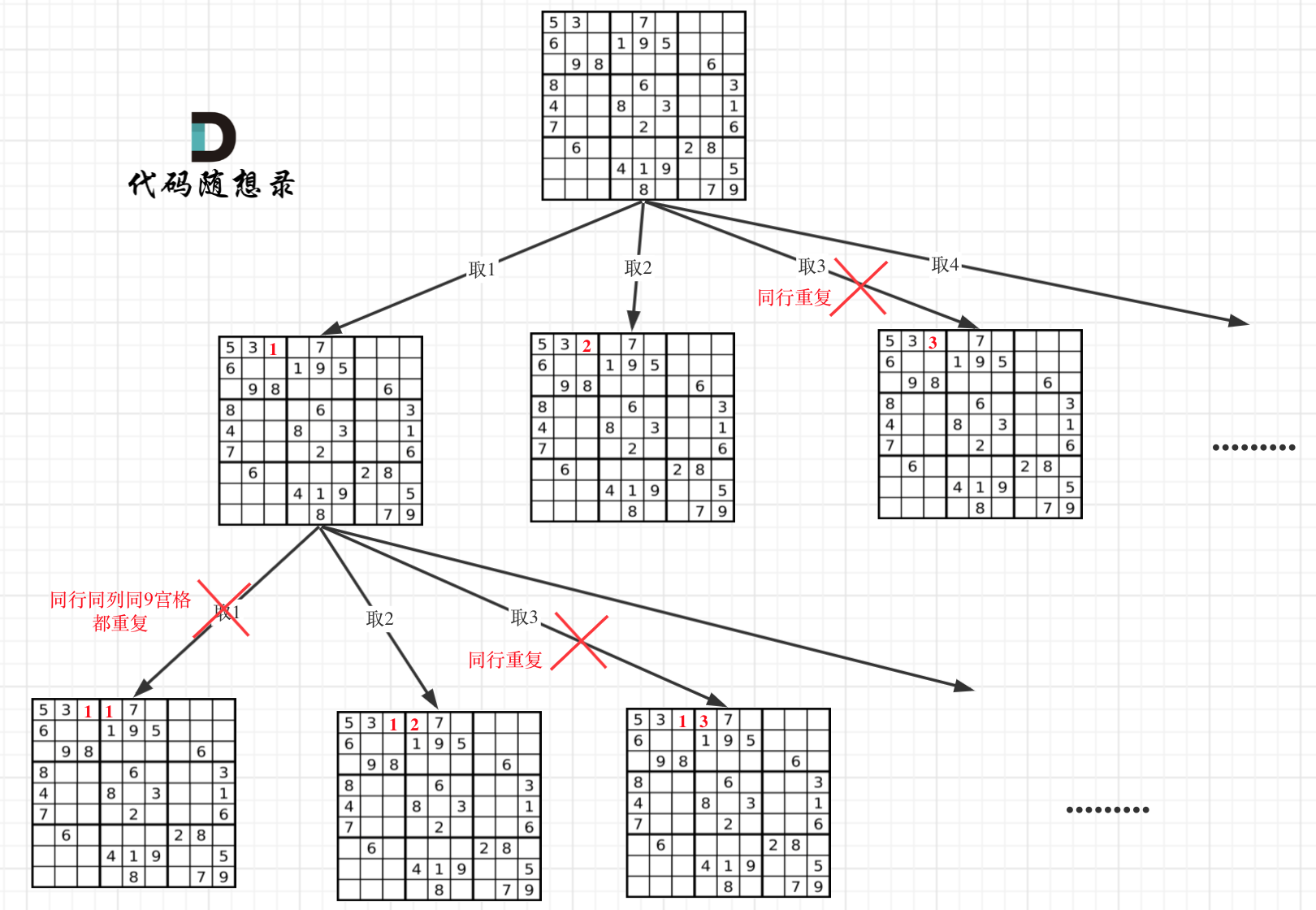
回溯三部曲
递归函数以及参数
递归函数的返回值需要是bool类型,为什么呢?
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
代码如下:
bool backtracking(vector<vector<char>>& board)
递归终止条件
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
不用终止条件会不会死循环?
递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
那么有没有永远填不满的情况呢?
这个问题我在递归单层搜索逻辑里再来讲!
递归单层搜索逻辑
 在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
代码如下:(详细看注释)
bool backtracking(vector<vector<char>>& board) {for (int i = 0; i < board.size(); i++) { // 遍历行for (int j = 0; j < board[0].size(); j++) { // 遍历列if (board[i][j] != '.') continue;for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适if (isValid(i, j, k, board)) {board[i][j] = k; // 放置kif (backtracking(board)) return true; // 如果找到合适一组立刻返回board[i][j] = '.'; // 回溯,撤销k}}return false; // 9个数都试完了,都不行,那么就返回false}}return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}注意这里return false的地方,这里放return false 是有讲究的。
因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解!
那么会直接返回, 这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!
判断棋盘是否合法
判断棋盘是否合法有如下三个维度:
同行是否重复
同列是否重复
9宫格里是否重复
代码如下:
bool isValid(int row, int col, char val, vector<vector<char>>& board) {for (int i = 0; i < 9; i++) { // 判断行里是否重复if (board[row][i] == val) {return false;}}for (int j = 0; j < 9; j++) { // 判断列里是否重复if (board[j][col] == val) {return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val ) {return false;}}}return true;
}最后整体C++代码如下:
class Solution {
private:
bool backtracking(vector<vector<char>>& board) {for (int i = 0; i < board.size(); i++) { // 遍历行for (int j = 0; j < board[0].size(); j++) { // 遍历列if (board[i][j] == '.') {for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适if (isValid(i, j, k, board)) {board[i][j] = k; // 放置kif (backtracking(board)) return true; // 如果找到合适一组立刻返回board[i][j] = '.'; // 回溯,撤销k}}return false; // 9个数都试完了,都不行,那么就返回false}}}return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {for (int i = 0; i < 9; i++) { // 判断行里是否重复if (board[row][i] == val) {return false;}}for (int j = 0; j < 9; j++) { // 判断列里是否重复if (board[j][col] == val) {return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val ) {return false;}}}return true;
}
public:void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};总结
解数独可以说是非常难的题目了,如果还一直停留在单层递归的逻辑中,这道题目可以让大家瞬间崩溃。
所以我在开篇就提到了二维递归,这也是我自创词汇,希望可以帮助大家理解解数独的搜索过程。
一波分析之后,再看代码会发现其实也不难,唯一难点就是理解二维递归的思维逻辑。
自己的代码
class Solution {bool isUsed(int row, int col, char k, vector<vector<char>>& board) {for (int i = 0; i < 9; i++) { //该列的后面(遍历这行)if (board[row][i] == k) return true;}for (int i = 0; i < 9; i++) { //(遍历这列)if (board[i][col] == k) return true;}int startRowIndex = (row / 3) * 3;//行的起始下标int startColIndex = (col / 3) * 3;//列的起始下标for (int i = startRowIndex; i < startRowIndex + 3; i++) {for (int j = startColIndex; j < startColIndex + 3; j++) {if (board[i][j] == k)return true;}}return false;}bool dfs(vector<vector<char>>& board, int row) {/*vector<vector<char>> temp = board;*/if (row == 9) return true;for (int col = 0; col < 9; col++) { //遍历该行的这些列if (board[row][col]=='.') { //这个列是空的需要填字。for (char k = '1'; k <= '9'; k++) { //该空格尝试1-9.if (isUsed(row, col, k, board)) continue; //这个数字在遍历过的列中已经填过了或者不满足棋盘条件。board[row][col] = k; //(row,col)位置填数字k.bool result = dfs(board, row);if (result) return true;board[row][col] = '.'; //(row,i)位置做檫除}return false;}}return dfs(board, row + 1);return true;}
public:void solveSudoku(vector<vector<char>>& board) {dfs(board, 0);}
};
相关文章:

回溯算法37:解数独
主要是我自己刷题的一些记录过程。如果有错可以指出哦,大家一起进步。 转载代码随想录 原文链接: 代码随想录 leetcode链接:37. 解数独 题目: 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则…...

【蓝桥杯-筑基篇】动态规划
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 1.最大连续子段和 2.LCS 最大公共子序列 3.LIS 最长上升子序列 4.数塔 5.最大子矩阵和 6.背包问题 ①01背包问题 ②完全背包 1.最大连续子段和 这段代码是一个求最大子数组和的算法,使用…...

Unity利用Photon PUN2框架快速实现多人在线游戏实例分享
简介 Photon 是一个泛用性的 ScoketServer 套装软件,可用于多人在线游戏、聊天室、大厅游戏,并同时支持 Windows、Unity3D、iOS、Android、Flash 等平台。Photon 包含两个部分,一部分是 Socket 服务器,另一部分是其针对各个平台编写的 SDK,Unity3D 平台对应的 SDK 为 Pho…...

ChatGPT直出1.5w字论文查重率才30% - 基于物联网技术的智能家居控制系统设计与实现
文章目录ChatGPT直出1.5w字论文查重率才30% - 基于物联网技术的智能家居控制系统设计与实现一、绪论1.1 研究背景与意义1.2 国内外研究现状分析1.3 研究内容与目标1.4 研究方向和思路二、物联网技术与智能家居概述2.1 物联网技术原理与应用2.2 智能家居的概念与发展历程2.3 智能…...

特斯拉的操作系统是用什么语言编写的?
总目录链接>> AutoSAR入门和实战系列总目录 文章目录特斯拉车辆操作系统特斯拉GitHub中使用的语言Ruby和GoPythonSwift 和 Objective CQt我们知道操作系统至少需要一些非常低级的代码,这些代码在系统首次启动时运行,必须使用接近硬件的语言编写。…...
C++学习8-C++提高编程
文章目录前言一、模板1.1 模板的概念1.2 函数模板1.2.1 函数模板语法1.2.2 函数模板注意事项1.2.3 函数模板案例复习:计算数组长度1.2.4 普通函数与函数模板的区别1.2.5 普通函数与函数模板的调用规则1.2.6 模板的局限性1.3 类模板1.3.1 类模板语法1.3.2 类模板与函…...

ubuntu安装git server
一安装 要在Ubuntu上安装Git服务器,需要按照以下步骤进行操作: 安装Git: sudo apt-get update sudo apt-get install git 创建一个Git用户和一个Git仓库目录: sudo adduser git sudo mkdir /home/git/repo.git sudo chown git:git /home/git/repo.git 初始化Git仓库: c…...

物流云数据分析平台
物流云数据分析服务平台 http://project.webcats.cn/bx/36569/2455/index.html 本次系统模拟的是湖南省数据,解释权归杭氏集团所有! 1、系统简介: 物流大数据集成展示系统旨在通过大屏幕全面显示指定地区的物流运营车辆、物流公司和货主的相关信息和…...
配置OBS存储功能、新搭建obs
通过应用开发环境与OBS(Object-based Storage Service)对接,实现对象或者Widget资产存储功能。 背景信息 对象存储服务(Object-based Storage Service,OBS)是一个基于对象的海量存储服务,为客…...
基于DPDK收包的suricata的安装和运行
操作系统版本:Ubuntu 20.04.5 suricata版本: suricata-7.0.0-rc1 suricata是一个基于规则的入侵检测和防御引擎,功能强大,但性能可能 差强人意,不过目前最新的7版本已经支持DPDK收包了,DPDK是Intel提供的高…...
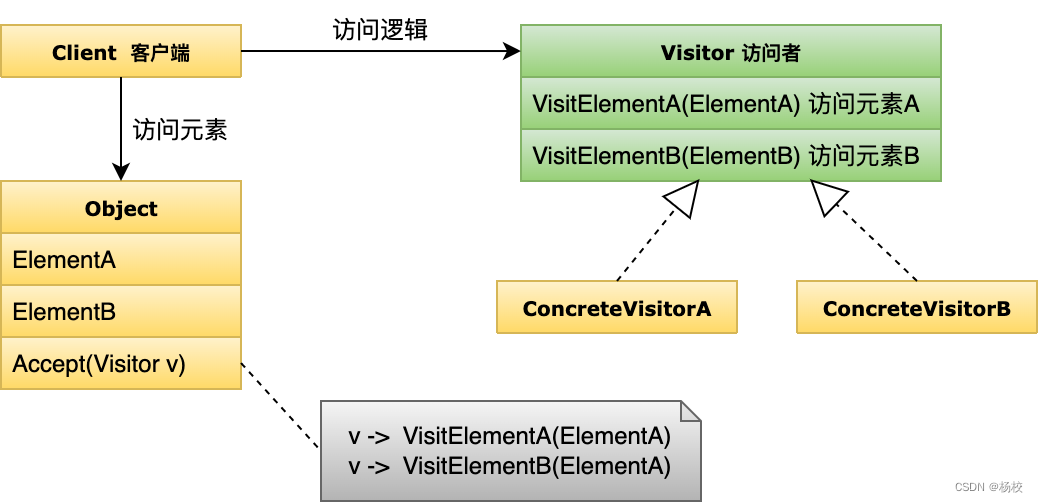
浅谈23种设计模式
创建型模式 有5种设计模式 抽象工厂(Abstract Factory):多套方案 抽象工厂模式是对创建不同的产品类型的抽象。对应到工作中,我们的确应该具备提供多套方案的能力,这也是我们常说的,要提供选择题。当你有这…...
JetBrains Rider 2022.3.3 Crack
具有 ReSharper 强大功能的令人难以置信的 .NET IDE!Rider 在我们使用 Windows 和 macOS 的整个开发团队中使用。 什么是骑士? JetBrains Rider 是一个基于 IntelliJ 平台和 ReSharper 的跨平台 .NET IDE。 支持许多 .NET 项目类型 JetBrains Rider 支持…...

浅理解扁平数据结构转Tree(树形结构)
文章目录📋前言🎯扁平数据结构🎯树形数据结构🎯使用递归将扁平数据转换为树形数据📝最后📋前言 在前端开发中,我们经常需要将扁平数据结构转换为树形结构(Tree)。比如在…...

前端开发——JavaScript的条件语句
世界不仅有黑,又或者白 世界而是一道精致的灰 ——Lungcen 目录 条件判断语句 if 语句 if else 语句 if else if else 语句 switch语句 break 关键字 case 子句 default语句 while循环语句 do while循环语句 for循环语句 for 循环中的三个表达式 for 循环嵌套 for …...

2.11 循环赛日程表
博主简介:一个爱打游戏的计算机专业学生博主主页: 夏驰和徐策所属专栏:算法设计与分析 目录 书本内容: 我的理解: 更优化的算法: 总结 1.注意实现问题 2.当用C语言和C实现循环赛日程表算法时ÿ…...

SpringBoot——SB整合mybatis案例(残缺版本)第三集
了解完使用阿里云存储的操作后,现在需要在案例里面集成阿里云进行开发。云服务——阿里云OSS的入门使用_北岭山脚鼠鼠的博客-CSDN博客 阿里云OSS——集成 对于前端传过来的图片要先上传到OSS,然后获取图片在云端的访问地址,存储到数据库里面…...
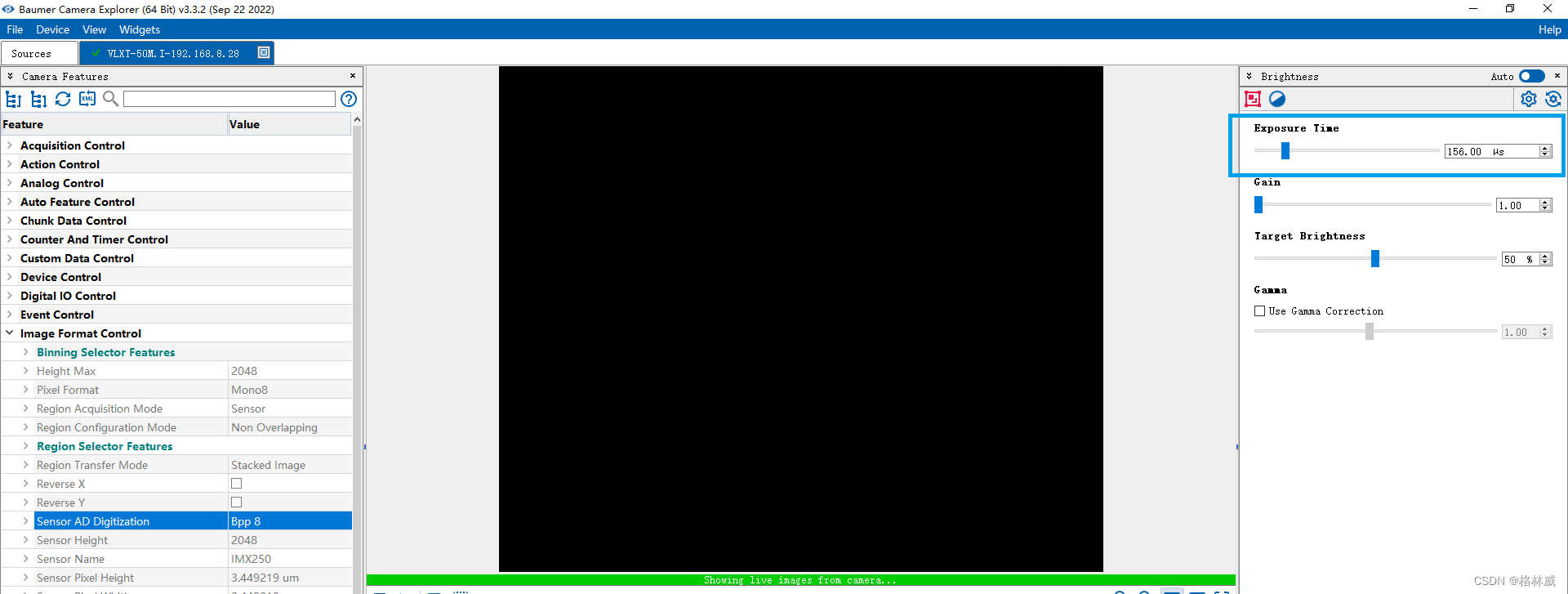
Baumer工业相机堡盟相机不满帧如何使用CameraExplorer设置相机参数让它的帧率达到满帧
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

巴黎爱情回忆 NFT 作品集
由 Metaverse Studio 制作。 欢迎来到浪漫之都巴黎!尽情游览美丽壮观的地标,探索法国文化。在离开之前,别忘了从《巴黎爱情回忆》NFT 作品集中带走一件纪念品。从世界著名的法国人物到标志性资产,这些 NFT肯定会为您的钱包带来巴黎…...
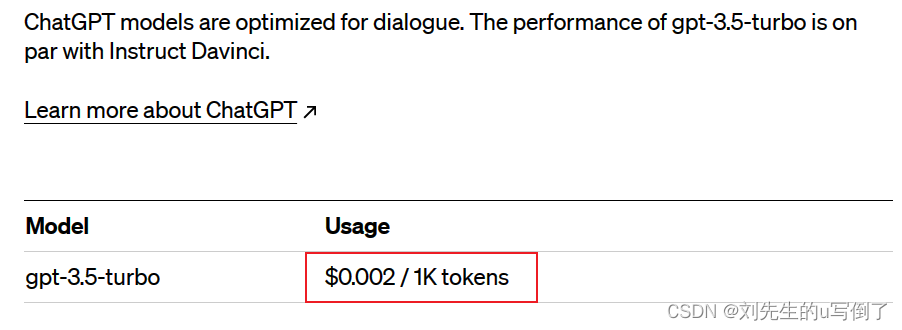
openai开放gpt3.5-turbo模型api,使用python即可写一个基于gpt的智能问答机器人
1安装python库 使用pip安装openai库,注意gpt3.5-turbo模型需要python>3.9的版本支持,本文演示的python版本是python3.10.10 pip install openai2创建api key 需要提前在openai官网上注册好账号,然后打开https://platform.openai.com/ac…...
GUI开发--LCD屏幕的使用(非第三方库)--笔记
导:界面交互需要GUI,GUI需要文字和图片,所有此处总结在M4芯片上实现GUI的基本操作!该芯片具有160K大小的内存,有512K的flash;故而没有使用第三方库! LCD屏幕的使用--笔记 1.汉字显示-两种方式…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
